异步电动机直接转矩控制磁链区间细分方法
2011-06-11王英常慧娟
王英,常慧娟
(大连交通大学 电气信息学院,辽宁 大连 116028)
0 引言
直接转矩控制用空间矢量分析的方法,在二相静止坐标系下计算并控制异步电动机的磁链和转矩,借助磁链和转矩滞环调节产生逆变器开关信号,从而获得转矩的高动态性能,解决了控制系统特性易受电机参数变化影响的问题[1-3].在传统6扇区控制的直接转矩控制系统中,低速时由于考虑定子电阻压降的影响,实现磁链位置角的精确计算比较困难,如果在一个扇区内选用一个电压矢量来同时实现定子磁链幅值和转矩的增加或减小,会导致磁链轨迹畸变,在扇区分界线附近尤为明显,严重影响系统性能[4].文献[5-6]采用常规的12扇区磁链细分方法,将6扇区的每个扇区平分为两个扇区,虽然改善了传统6扇区控制方法的磁链内陷问题,提高了响应速度,但并没有完全解决由于磁链观测不精确而选择容易错误的空间电压矢量的问题.本文分析研究了改进12扇区磁链细分方法和常规12扇区细分方法,建立了Matlab环境下两种磁链细分方法的DTC系统仿真模型,理论分析和仿真试验表明,改进的12区间磁链控制方法在磁链观测不够精确的情况下能表现出更好的控制性能,磁链幅值能始终保持在容差范围内,转矩脉动较常规12扇区磁链细分方法有明显减小.
1 直接转矩控制的基本原理
电机电磁转矩也就是定子磁链和转子磁链相互作用的结果,可写成如下形式:
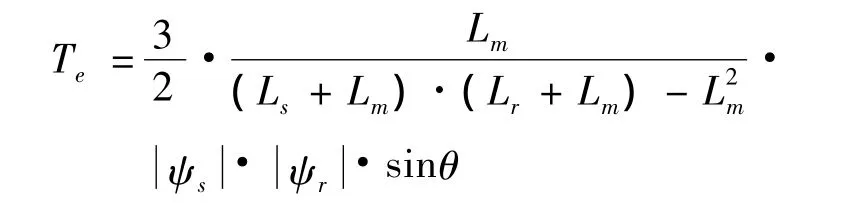
由上式可以看出,电机转矩与定子、转子磁链幅值及磁通角有关.实际运行中,为了充分利用铁心,通常保持定子磁链幅值为恒定值,转子磁链幅值由负载决定.因此,通过改变磁通角的大小就可以改变电磁转矩.由于转子磁链旋转变化较定子缓慢,通过控制定子磁链的旋转速度即可改变磁通角的大小,电机的定子磁链和定子电压存在积分关系,因此可以选择合适的电压空间矢量来控制定子磁链的旋转速度,从而改变磁通角的大小,以达到控制电机转矩的目的.
图1为异步电机直接转矩控制的原理图,将电机检测出的转速与目标转速比较,通过PID调节器生成目标转矩指令,检测出的定子电压及电流,通过磁链和转矩观测器得出定子磁链观测值和实际电磁转矩,经过磁链和转矩的滞环调节,根据定子磁链所在区域,不断切换逆变器的开关状态使定子磁链轨迹逼近于圆形,并通过零状态电压矢量的穿插调节来改变转差频率,以控制电机的转矩及其变化率,使异步电机的转矩和磁链能同时按要求变化.

图1 直接转矩控制原理图
2 12扇区的磁链区间细分方法
2.1 常规的12扇区磁链细分方法
图2为传统6扇区磁链轨迹划分图,由图可以看出,电压空间矢量U3在扇区S2内的作用是增加磁链幅值,增加转矩,而在扇区S1内的作用是减小磁链,增加转矩,电压空间矢量U3方向正好与S1和S2分界线垂直,因此在两扇区分界即磁链位置角为π/6处,磁链位置估计上有一点误差就会使系统选择错误的电压空间矢量.例如由磁链调节器和转矩调节器的输出信号判断需要减小磁链,磁链实际运行在扇区S2,但由于定子电阻的影响,在磁链观测上有误差,错误地认为磁链运行在扇区S1,从而选择了空间电压矢量U3来减少磁链,但事实却增加了磁链幅值,使磁链幅值更大,从而造成了磁链较大的脉动,使磁链轨迹在扇区分界线附近严重畸变.
由以上分析可知,采用6扇区的电压矢量选择表,在扇区分界线附近,对磁链的估计要求非常严格.而考虑定子电阻变化的影响,很难实现磁链位置的准确观测.
此外,一个扇区内,定子电压对定子磁链作用是不平衡的[7],导致定子磁链轨迹在一个扇区内并非均匀变化,在区段分界线附近尤为明显.这将导致磁链轨迹不再接近圆形,从而引起电流畸变,系统性能变差.文献[5-6]针对定子电压对磁链作用不平衡这一问题,采用一种常规的12扇区磁链细分方法改进了这一问题.

图2 6扇区磁链轨迹划分图
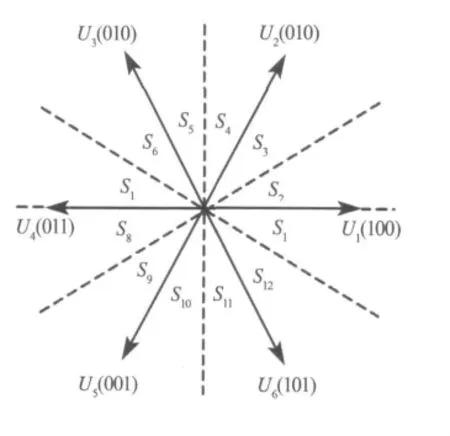
图3 常规12扇区磁链轨迹划分图
常规的12扇区磁链细分方法将原来的一个扇区平分为两个扇区,以[0,π/6]为第一扇区,使每个扇区可供选择的电压矢量由原来的两个变为了四个,用到了传统6扇区划分时无法用到的电压矢量U1和U4,但它只是减小了在扇区分界线处选择错误空间电压矢量的概率,并没有完全避免这种情况的发生.如图3所示,在扇区S1,需要增大磁链,增大转矩时,可选择U1或U2,在扇区S2,同样的情况可选择U2,为了避免在这两个扇区分界线处磁链观测有误差,则只能舍弃U1.在这两个扇区里都选择U2来增大磁链增大转矩.而U2在S12内的作用是减小磁链,增大转矩,与在S1扇区内对磁链的作用相反,这样,如果在S1和S12的分界线处磁链区间判断错误,就会选择错误的空间电压矢量,原本要增大磁链结果却减小了磁链,造成磁链轨迹畸变.
2.2 改进的12扇区的磁链细分方法及改进的电压空间矢量选择表
改进的磁链细分方法如图4所示,图中第1扇区为[-12/π,12/π],由图可以看出,改进的扇区划分避免了扇区分界线与电压矢量垂直的情况,选择电压矢量时同样也用到了电压空间矢量U1和U4,避免了常规12扇区磁链细分方法在扇区分界线处因为担心扇区判断错误而不知道选择哪个电压矢量的困扰,解决了在扇区分界线处由于磁链位置判断不够精确而容易选择错误的空间电压矢量的问题.

图4 改进12扇区磁链轨迹划分图
根据改进的磁链扇区划分方法制定的空间电压矢量选择表如附表所示.

附表 优化的12扇区空间电压矢量选择表
3 仿真试验及结果
在MATLAB/Simulink下建立异步电动机直接转矩控制系统仿真模型,如图5所示,测得异步电动机定子电压和电流,经坐标变换后送到磁链和转矩观测器,系统中定子磁链和电磁转矩由磁链和转矩观测器得到,电动机实际转速与给定信号进行比较后加到PI调节器,由PI调节器的输出作为转矩给定信号.磁链区间判别单元将定子磁链分成12个扇区,再综合磁链调节器和转矩调节器的输出信号,运用空间电压开关表和MATLAB函数选择空间电压矢量.通过改变模型中的MATLAB函数和设置不同的空间电压矢量选择表来分别对采用两种方法的系统进行仿真分析.
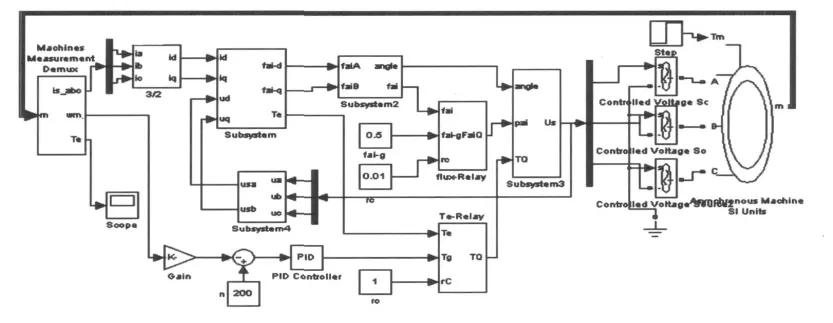
图5 异步电动机直接转矩控制仿真模型
仿真所用异步电机参数为:额定频率PN=3730 W,额定电压UN=460 V,额定频率fN=60 Hz,定子电阻 Rs=1.115 Ω,转子电阻 Rr=1.083 Ω,定子电感 Ls=0.005 974 H,转子电感 Lr=0.005 974 H,互感 Lm=0.203 7 H,极对数 np=2,转动惯量 J=0.02 kg·m2,Ψ*=0.5 Wb,εΨ=0.1 Wb,εT=1 N·m.
仿真时,ω*r=200 rad/min,仿真时间为0.25 s,在0.1 s时,突加TL=5 N·m 的负载.
图6为当定子磁链相位角观测误差为 ±π/12时的两种磁链细分方法的磁链轨迹和转矩响应曲线,从波形可以看出,采用常规的12扇区磁链细分方法在磁链相位角观测有误差的情况下,磁链轨迹在部分扇区分界线处有明显畸变,此时表现在转矩响应上,转矩脉动明显增大,最大转矩脉动为12.5%.采用改进的12扇区磁链细分方法体现了较大的优势,磁链幅值始终保持在容差范围之内,并不受磁链观测精确度的影响,转矩脉动较常规12扇区磁链细分方法有明显减小,减小为6.25%.总之,采用改进的12区间磁链细分方法具有更好控制性能.
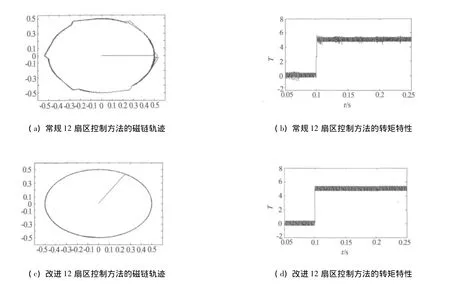
图6 磁链观测有误差时两种磁链细分方法的磁链轨迹和转矩特性
4 结论
本文分析比较了两种磁链细分方法的优缺点,并分别对采用此两种方法的异步电动机直接转矩控制系统进行仿真.理论分析和仿真结果均表明,常规的12扇区细分方法控制有较快的动态响应速度,但在磁链观测不够精确时磁链轨迹会发生畸变,转矩脉动增大,改进方法在任何情况下都能表现良好的性能.
[1]李华德.交流调速控制系统[M].北京:电子工业出版社,2003:171-174.
[2]梅柏杉,陈晖.直接转矩控制系统性能改善的仿真研究[J].电机与控制应用,2009,36(2):33-35.
[3] LASCU C,TRZYNADLOWSKIAM.Combining the principles of sliding mode,direct torque control and space vector modulation in a high performance sensorless AC drive[J].IEEE Transactions on Industry Applications,2004,401,40(1):170-177.
[4]廖晓钟,邵立伟.直接转矩控制的12区段控制方法[J].中国电机工程学报,2006,26(6):167-172.
[5]丁惜瀛,夏强等.直接转矩控制磁链低频脉动分析及抑制[J].电气技术,2008(9):46-50.
[6]郭嘉强,喻寿益.一种改进异步电机直接转矩控制系统性能的方法[J].电气传动,2008,38(9):18-21.
[7]廖晓钟,马克明,周乐芳.一种细分空间的PWM波形实时生成方法[J].电气传动,2004(3):13-15.
