船舶电力负荷中电动机的动态建模与仿真

李东辉，张均东，纪玉龙

(1.大连海事大学轮机工程学院，辽宁大连116026;2.大连交通大学电气信息学院，辽宁大连116028)

0 引言

目前，随着计算机技术的迅猛发展，电力系统的计算机仿真已成为电力系统设计、规划、运行及故障分析的重要工具，然而，其仿真结果有时无法重现真实的动态过程，与实际的电力系统有着一定的误差，误差的大小及性质对该决策的正确性具有决定作用.而产生误差的主要因素就是负荷模型不够准确.很多研究者指出负荷特性对电力系统仿真有着很大的影响，这表现在不同的负荷特性对电力系统的暂态稳定、电压稳定、低频振荡等具有不同程度的影响，在临界情况下，仿真结果可能发生质的变化［1］.

近年来，在电动机建模研究方面，有学者考虑了铁心饱和和深导条效应，提出了新的仿真方法用于三相鼠笼异步电动机的暂态研究，其数学模型由六阶关于电压，电流的微分方程组表示［2］.有的文献提出了反映从10～10 MHz宽频率范围响应特性的三相电动机的模型［3］.有的学者计及气隙空间谐波效应产生的负载杂散损耗，在简化的电动机等效电路中用与定子电抗串联的附加电阻来反映损耗，并做了实验验证［4］.还有文献研究了两个经常使用的双鼠笼电动机模型的等效问题，提出了等效参数［5］.针对非对称定子铁心故障，有文献建立了动态电动机模型，用每相的等效铁型损耗电阻变化来建立故障模型［6］.还有学者综述了用于潮流和长期电压稳定性研究的静态三相异步电动机的模型，选择了代表不同工作区域的最合适的电动机模型［7］.2011年，贺仁睦等在进行负荷建模时以电压和频率作为输入量，将建立的负荷模型应用于实际系统［8］.上述各类电动机模型，应用于不同的场合，等效模型各有侧重，可以为后来的研究者提供方向和基础支持.

影响电力系统仿真精度的关键因素之一就是负荷模型比较粗略.针对不同的仿真目的和仿真精度要求，必须确定重要负荷的负荷特性和模型［9］.船舶电力系统的容量小，其电压、频率较陆上大容量电力系统更不稳定，所以，在满足运算速度的前提下，应采用动态负荷模型来提高电站模拟器的仿真精度.本文考虑到电动机类负荷在船舶电力负荷中占有很大比例，而且其暂态过程大大影响负荷的动态特性.尤其电压剧烈变化时，要合理描述电压暂降过程中敏感设备的异常运行对综合负荷功率变化的影响［11］.构造负荷动态模型可以减少运算误差，提高船舶电站模拟器的仿真逼真度.根据仿真或计算需要，针对不同的情况所需的精度要求，可以采用不同的负荷模型.考虑到船舶电站仿真的精度和实时性要求，在动态仿真时，如加载和卸载、短路故障仿真等，可以采用比较精确的高阶感应电动机模型，如考虑电动机机电暂态过程模型.而对于准稳态仿真，可简化数学模型，采用考虑机械暂态的变阻抗数学模型.

1 电动机负荷建模

由于实际电力系统不能让电压和频率大范围变化，获得准确的负荷动态特性比较困难，加之负荷时变性、随机性、多样性等特点，目前动态负荷建模是世界公认的尚未完全解决的难题.不同国家的学者从不同的角度，采用不同的方法，建立了很多负荷模型，进行了多方面有益的探索［9-12］.负荷建模领域现在有两大发展方向:综合测辨法与统计综合法.目前，负荷模型与实际情况还有较大差距，常用的负荷建模模方法还是机理分析式的.

1.1 考虑机械暂态的电动机变阻抗数学模型

如图1所示为计及电动机机械暂态的准稳态等值电路.其中，铁损等效电阻为Rm;定转子间的互感抗为Xm;定子的漏电抗是X1;转子的漏电抗是X2;转子绕组的等值电阻为R2.系统角频率为ω;电机角速度为ωm，而电机的转差率为:s=(ω－ωm)/ω，服从电机的转子运动方程

式中，TJ为电动机转子与机械负载的等值转动惯量;Tm表示机械负载转矩;Te表示电动机的电磁转矩.不考虑电磁暂态过程时，其电磁转矩表达式为:

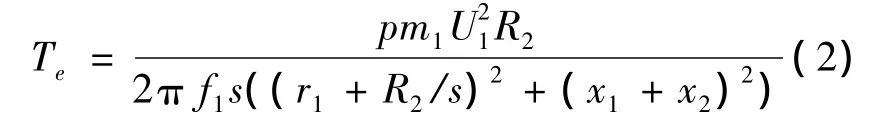
式中，U1为电网电压有效值;P为感应电动机转子的磁极对数.m1和f1分别为感应电动机的相数和电网电压的频率.电动机的机械转矩取决于机械负载的性质，看作是电动机转差率的函数，表达如式(3)式所示:

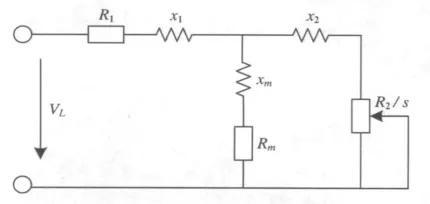
图1 感应电动机的等值电路

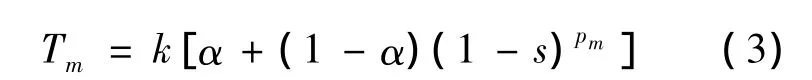
式中，参数α表示是恒转矩部分在机械负载转矩中所占的比例，与电动机转速无关;Pm为与电动机机械负载特性有关的指数;k为电动机的负荷率.

由感应电动机的等值电路图可以得到感应电动机的等值阻抗为:

显然，电动机的等值阻抗是转差s的函数，如果电网频率变化，可以考虑实际频率与额定频率比值来调整电抗参数.电网电压的变化也可以用实际电压与额定电压比值来修正.根据电动机的转子运动方程，求出转差随时间变化曲线，于是等效阻抗随时间变化关系可以得到.进一步可以求出定子电流、转子电流等曲线.采用变阻抗方法建立电动机模型可以将电力系统的微分代数方程组简化为微分状态方程组，便于求解.由式(1)～(4)可在构成基于Simulink的异步电动机仿真模块，如图2所示.

图2 异步电动机仿真模块图

1.2 考虑电磁暂态和机械暂态的电动机数学模型

Simulink中的异步电动机模块来源于四阶感应电动机的数学模型，考虑了电磁暂态和机械暂态，相对比较复杂.该模块可以在发电或电动状态下运行.电气部分由四阶状态方程组代表;机械部分则为二阶系统.各方程式如下，电气系统:

以上式中P=d/dt为微分算子;Rs为定子电阻;Rr为转子电阻;Lls为定子漏感;Llr为转子漏感;Lm为定转子间的互感;Ls为定子总电感;Lr为转子总电感;ω为电机同步角频率;ωr为电动机转子角频率;ωm为电动机转子的电气角速度;Vds为d轴定子电压;Vdr为d轴转子电压;Vqs为q轴定子电压;Vqr为q轴转子电压;ids为d轴定子电流;idr为d轴转子电流;iqs为q轴定子电流;iqr为q轴转子电流;φds为d轴定子磁链;φdr为d轴转子磁链;φqs为q轴定子磁链;φqr为q轴转子磁链;Te为电磁转矩;Tm为机械转矩;P为极对数;H为转子和负载惯量常数.式(5)～(11)就构成了异步电动机在dq坐标系下的数学模型.

2 仿真与结果分析

图2为采用变阻抗方法等效的异步电动机仿真模块图.图中power system模块构成三相电源系统，transform system模块构成abc-dqo坐标变换;frequency system模块构成频率变化模型;induction motor模块反映异步电动机的变阻抗模型，包括dqo-abc坐标变换;EM system模块反映电压变化模型.对比图3与图4的定子电流，可以看出，启动开始后0～0.2 s阶段，由于忽略了电磁暂态，变阻抗的电动机模型定子电流衰减得相对较快，0.2～0.4 s阶段，电流值比四阶电动机模型的值小一些，出现一些误差.启动后0.4 s后进入稳态运行，两者的电流值比较接近.对比图5与图6电磁转矩曲线，同样的机械负载情况下，电机起动的前0～0.2 s阶段，由于忽略了电磁暂态，变阻抗的电动机模型转矩低频振荡部分衰减得相对很快，0.2～0.4 s阶段，转矩值比四阶电动机模型的值大一点，启动后0.4 s后进入稳态运行，两者的转矩值比较接近.如图7为变阻抗模型的电动机星－三角起动过程中定子电流仿真曲线，其最大值接近20 A，启动4 s后电动机三角形全压供电时，电流开始在10 A左右，然后稳定在7 A.图8为变阻抗模型的电动机直接全压起动的定子电流仿真曲线，起动时最大定子电流接近60 A，而这完全符合电动机星－三角起动过程实际情况.变阻抗方法构造的电动机模型仿真结果与simulink组件中四阶电动机模块的仿真结果比较吻合.可以说明该方法建模的有效性和简便性.

图3 电动机启动时定子电流仿真图(变阻抗模型)

图4 四阶模型电动机的定子电流仿真曲线

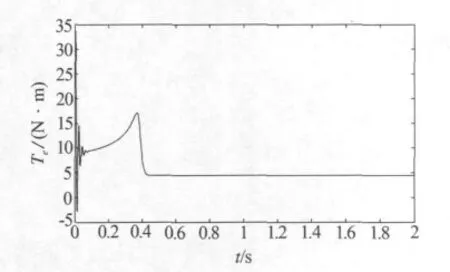
图5 电动机的电磁转矩仿真曲线(变阻抗模型)

图6 四阶模型电动机的电磁转矩仿真曲线

图7 电动机Y-Δ起动过程定子电流仿真曲线(变阻抗模型)

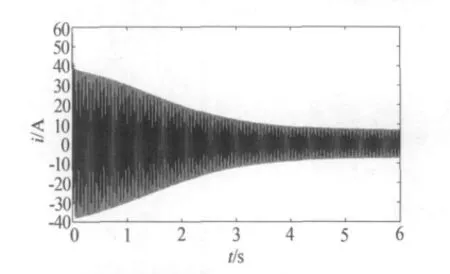
图8 电动机全压起动过程定子电流仿真曲线(变阻抗模型)

3 结论

本文根据船舶电站模拟器动态仿真的需要，以稳态运行电动机模型为基础，考虑了转差率，电网频率及电压变化的影响，提出了考虑机械暂态的变阻抗电动机数学模型.利用Matlab软件中的Simulink基本模块搭建了变阻抗电动机仿真模型，该模型同考虑机械和电磁暂态的四阶电动机模型进行了比较，定子电流，电磁转矩曲线仿真结果表明该建模方法正确有效.发现在电动机参数较少条件下，采用变阻抗方法构造的电动机仿真模型能够满足模拟器仿真精度和运算速度要求.该模型已用于多项船舶电站模拟器的研制中.

［1］邵自甦.电力负荷建模在电力系统中的重要意义［J］.内蒙古石油化工，2006(8):100-102.

［2］IKEDA M，HIYAMA T.Simulation Studies of the Transients of Squirrel-Cage Induction Motors［J］.IEEE Transactions on Energy Conversion，2007，22(2):233-239.

［3］MIRAFZAl B，SKIBINSKI G L，TALLAM R M，et al.Universal Induction Motor Model With Low-to-High Frequency-Response Characteristics［J］.IEEE Transactions on Industry Applications，2007，43(5):1233-1246.

［4］BOGLIETTI A，CAVAGNINO A，FERRARIS L，et al.Induction Motor Equivalent Circuit Including the Stray Load Losses in the Machine Power Balance［J］.IEEE Transactions on Energy Conversion，2008，23(3):796-803.

［5］PEDRA J，CANDELA I，SAINZ L.Modelling of squirrel-cage induction motors for electromagnetic transient programs［J］.Electric Power Applications，IET，2009，3(2):111-122.

［6］BARRERA DE LA，BOSSIO P M，SOLSONA G R，et al.Model for three-phase induction motors with stator core faults［J］.Electric Power Applications，IET，2010，4(8):591-602.

［7］CARMONA-SÁNCHEZ J，RUIZ-VEGA D.Review of static induction motor models［C］.North American Power Symposium(NAPS)，2010(1):1-8.

［8］贺仁睦，叶静，徐欢，等.计及频率特性的实测负荷建模［J］.电工技术学报，2011，26(5):165-170，183.

［9］张红斌.电力系统负荷模型结构与参数辨识的研究［D］.北京:华北电力大学，2003.

［10］李欣然，钱军，王立德，等.配电网集结等效的异步电动机综合负荷模型及其总体测辨建模［J］.电工技术学报，2009，24(4):175-185.

［11］李妍，张步涵，尹项根.电压暂降过程中敏感动态负荷建模问题研究［J］.水电能源科学，2006，24(4):83-85.

［12］石景海.考虑负荷时变性的大区电网负荷建模研究［D］.北京:华北电力大学，2004.