汽车玻璃曲面展开系统研究与开发

沙智华，陈翠翠，张生芳

(大连交通大学 机械工程学院，辽宁 大连 116028)

0 引言

为了满足空气动力学、光学失真、汽车整体造型美观、白车身型面限制等要求［1-2］，汽车前、后挡风玻璃一般都设计为双曲A级曲面，且整个曲面常由几个分曲面复合而成.从加工工艺的角度出发，必须以曲面的设计模型为依据利用复杂曲面展开技术求取展开毛坯模型.一般CAD软件，例如CATIA，都具有简单的复杂曲面展开功能，但对于设计复杂且曲面质量要求严格的不可展曲面常出现展开运算无法进行的问题，而不能实现复杂曲面的展开.因此，汽车玻璃曲面展开技术是其制造中的一个难点.基于汽车玻璃曲面几何特点，本文提出曲线映射复杂曲面展开法，并开发了汽车玻璃曲面展开系统，实现了曲面高精度展开和汽车玻璃毛坯模型的自动生成.

1 汽车玻璃曲面展开系统总体设计

1.1 曲线映射展开法原理

本文以某车型汽车前挡风玻璃曲面为例，对其进行曲率分析如图1所示:曲面曲率分析1是整个曲面曲率的色标显示结果，箭状曲率分析1是横向主截面A-A和纵向中心截面B-B箭状曲率分布，箭状曲率分析3是曲面边界的曲率分析图.可以看出:汽车玻璃曲面是一种双曲分布、曲率均匀变化、沿纵向中心截面对称分布、拐角处曲率较大的A级复合式曲面.

图1 汽车玻璃曲面模型及其曲率分析

目前存在的复杂曲面展开方法主要有几何展开法、力学/能量展开法［3-7］两类，这些方法的核心思想都是围绕解决一个或多个几何变量组合的变形最小化或变形能平衡问题展开的［4］，研究思路可总结为:首先对曲面进行三角网格划分，基于一定的展开原则和策略对曲面进行几何法初始展开，再针对展开中出现的叠片、裂纹、翻转和变形等进行力学/能量法调整、优化.但这些方法存在计算量大、算法效率低、处理过程复杂等问题，且在展开过程中会产生二次误差［8］.

针对这些方法的不足和汽车玻璃曲面的特点，本文提出了曲线映射复杂曲面展开法.其基本思想是离散化，即将无法精确求解的连续物体离散为有限单元体，用离散单元体的解近似代替连续物体求解来解决实际问题.基于这种思想，曲线映射法的原理为:假设曲面材料为各向同性，首先将复杂曲面离散成有限的曲线单元体，这样复杂曲面展开问题就转化为曲面上的曲线展开成直线的问题;然后为保持曲面展开前后面积不变，将曲面上的曲线按照弧长不变的原则和角度对应关系映射到平面上，得到曲线在平面上展开的映射点;最后用光滑的曲线连接这些映射点就得到了曲面展开轮廓.

这种曲线映射展开法采用曲线代替曲面，减少了传统的用三角网格代替曲面而造成的曲面展开累积误差，提高了展开精度;同时，展开对象从曲面转化为曲线，简化了处理过程，避免了传统展开方法出现的裂纹、翻转、变形等情况，使系统易于实现.

1.2 汽车玻璃曲面展开系统实现流程

基于上述曲线映射展开法原理，本文以Visual C++为平台，采用OpenGL图形处理接口开发了汽车玻璃曲面展开系统，该系统开发流程如图2所示.

首先，读取曲面点集坐标值信息，用双三次准均匀有理B样条曲面对汽车玻璃进行建模及曲面重构;然后，设置曲面展开精度参数，绘制与曲面相交的平面族，利用曲面求交获得曲面上的曲线并计算曲线弧长;接着，以弧长不变的原则将曲面上的曲线按照角度对应关系映射到平面上，得到曲线在平面上展开的映射点，用B样条曲线插值法连接这些映射点就得到曲面展开轮廓;最后，检验展开结果是否满足系统的精度要求，如果是则输出曲面展开结果，否则返回到设置曲面展开精度参数步骤，重新进行曲面展开.

由曲面展开流程可以看出，曲面展开系统主要由读取点集信息、曲面建模与重构、获取曲面上的曲线、曲线映射展开等四部分组成，下面分别对其关键技术做进一步介绍.

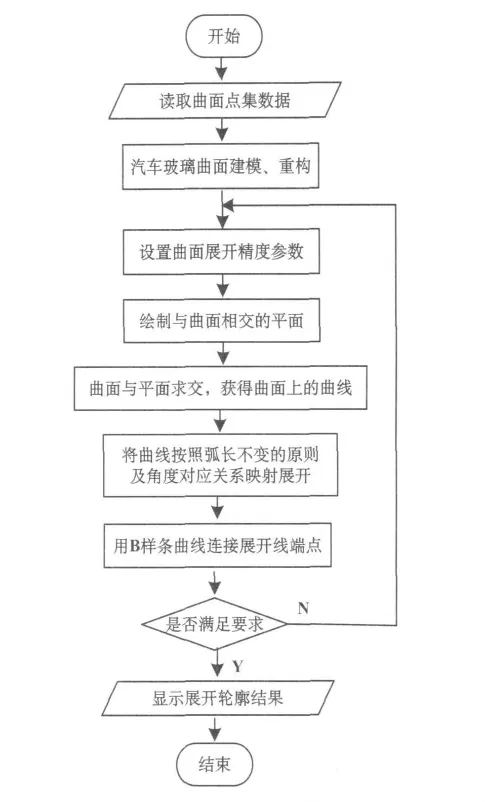
图2 汽车玻璃曲面展开系统流程图

2 曲面建模与重构

通常，汽车玻璃曲面模型是利用软件通过复杂的调面过程得到的，没有具体的数学描述模型，而建立曲面数学模型与曲面几何模型重构是汽车玻璃曲面展开系统的基础.因此，本文首先获取汽车玻璃曲面点集(型值点)信息，然后对曲面进行建模与重构，建立曲面展开系统研究对象.

2.1 采集曲面点集

为保证曲面模型不失真，要求采集的曲面点集尽量均匀、密集、有序且必须包含边界点.

本文采集曲面点集的方法为:首先，将曲面划分为上侧边界、曲面主体、下侧边界三个区域;接着，过曲面纵向中心截面的中间控制点作曲面的切面，有顺序地建立与此切面互相垂直、保持等距间隔的交叉平面族;然后，将这些平面族分别与曲面上侧边界、曲面主体、曲面下侧边界求交，即可得到具有一定规律的有序交点集;最后，分区选择曲面交点集，测量这些交点的三维坐标值，并按顺序保存在文本文档中.

利用这种方法，本文应用 Visual Basic对CATIA进行自动化对象编程实现曲面模型点集信息的采集.基于汽车玻璃曲面的对称性，取曲面一半作为系统研究对象，当平面族间隔距离为40mm时，取得19×16型值点，如图3所示.

图3 采集的曲面点集

2.2 曲面建模

汽车玻璃曲面是由自由型曲线、曲面构成的复杂空间曲面，而B样条方法能够精确表示和设计自由型曲线、曲面.基于这一点，根据汽车玻璃曲面几何特点及采集的曲面点集信息，本文确定采用双三次准均匀有理B样条曲面对汽车玻璃曲面进行描述.其数学模型为:

式中，p(u，v)为张量积B样条曲面;Di，j(i=0，1，…，mm －1;j=0，1，…，nn－1)为曲面控制顶点;Ni，k(u)和Nj，l(v)分别为沿u向的k次和沿v向的l次 B样条基函数并由节点矢量 U(u0，u1，…，um+k+1)和 V(v0，v1，…，vn+l+1)按德布尔-考克斯公式决定.

由式(1)可以看出:B样条曲面模型是由曲面控制顶点和节点矢量决定的，而不是曲面型值点.本文通过采集曲面点集获得曲面型值点，利用这些型值点来计算控制顶点及节点矢量，从而得到B样条曲面模型，这个过程称为B样条曲面反算，其中型值点个数m×n与控制顶点个数mm×nn的关系为mm=m+k－1，nn=n+l－1;B样条曲面节点矢量采用规范累积弦长参数化方法计算可得.

对于本文汽车玻璃B样条曲面模型:m=19，n=16，k=l=3 ，曲面控制顶点可由19×16型值点反算求得，节点矢量计算可得

将控制顶点及节点矢量代入式(1)即可得到曲面数学模型.

基于汽车玻璃B样条曲面数学模型及Open-GL二维求值器机理，利用B样条曲面绘制函数实现汽车玻璃重构曲面在系统窗口的显示.同时，为方便系统实现，过曲面纵向中心截面的中间控制点(Ox，Oy，Oz)建立用户坐标系，其中XOY面是曲面的切面.如图4所示曲面重构结果及用户坐标系.

图4 B样条重构曲面、控制顶点及控制网格

3 获取曲面上的曲线——曲面求交

获取曲面上的曲线是曲线映射展开法及汽车玻璃曲面展开系统实现的关键.本文中曲面上的曲线通过曲面与平面求交的方法获得，其步骤为:首先构建与曲面相交的平面族;然后曲面与平面求交，获得曲面上的曲线;最后计算曲线弧长.

3.1 构建与曲面相交的平面族

本文以曲面纵向中心截面的中间控制点为展开基点，这样可以有效的抵消曲面对称方向的累积误差，提高了展开精度.过展开基点建立与XOY面垂直、呈等角α辐射状分布的平面族，平面的数量为t，则有(t－1)·α =180°.通过这些平面与曲面求交获得的曲线也是过展开基点呈等角辐射分布状，从而避免了网状曲线双向延展的问题，使系统处理过程更加简洁.

在系统实现过程中，这些呈辐射分布的平面族是利用过空间任一旋转轴的旋转矩阵T实现的.

3.2 曲面求交及弧长计算

曲面参数方程为式(1)，平面族代数方程采用点法式表示为:

将式(1)、式(2)联立得曲面与平面的交线方程为:

式(3)是一个以u和v为变量的二元非线性方程.理论上，可令其中一个变量u以定步长变化，而后求解一元高次非线性方程组，进而得到交点(px(u，v)，py(u，v)，pz(u，v))，但实际上交线方程次数非常高、难以计算.本文采用改进的数值搜索法进行曲面求交，避免一元高次方程的求解，其方法为:令变量u和分别以定步长δ1、δ2进行搜索，(px(u，v)，py(u，v)，pz(u，v))为曲面上的精确点，若此点到曲面的距离小于或等于ε即满足式(4)则此点即为交线上的点，ε为交点逼近曲面的误差准则，根据交点间的关系将多个交点连接起来就得到了交线即曲面上的曲线.曲线弧长利用交点线段距离累加得到.曲面求交及弧长计算的精度是由误差准则ε和参数u、v的搜索步长δ1、δ2来保障的.

在系统实现过程中，主要采用两种方法来优化程序:其一是对不同转角范围内的交线采用分别处理法，假设转角为 β，当 β =0°时，v=0，u从0递增到0.5;当0°＜ β＜90°时，u从0递增到0.5，v从1递减到0;β =90°时，u=0，v从1递减到0;90°＜ β＜ 180°时，u从1递减到0.5，v从1递减到0;β =180°时，v=0，u从1递减到0.5.其二是利用平面斜率的特点，以0°＜β＜90°为例进行说明，若u=ui、v=vj时获得一个交点，那么下个交点的搜索起始位置为u=ui+δ1、v=vj，而不是v=1.这两种处理方法大大减少了程序中不必要的循环和计算，同时又能避免在相同v、不同的u下取得重复交点的问题，提高了交线计算的准确性.

当 α =6°，ε =0.02mm，δ1= δ2=0.05mm时，得到曲面上的曲线结果如图5所示.

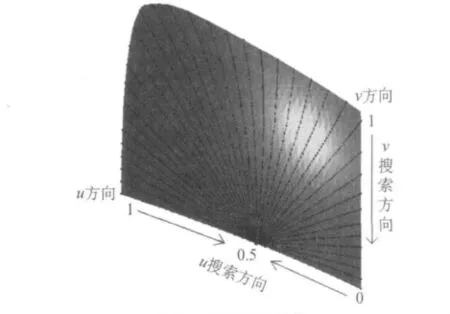
图5 曲面上的曲线

4 曲线映射展开

获得曲线弧长之后，曲线就要按照弧长不变的原则和角度对应关系映射到平面上.映射平面为XOY面.由于求交平面是呈等角a辐射分布的，根据角度对应关系，曲线在平面上的展开直线也是等角分布.因此第i条曲线映射到平面的过称为:

输入:展开直线斜率ki=tan(i·α)，展开直线起点都为展开基点(Ox，Oy，Oz)，直线长度 l=L弧长.

映射关系:求解方程组

输出:展开直线端点(xi，yi，Oz)即为曲线在平面上的映射点.

最后，将展开曲线的端点利用三次B样条曲线进行插值，即可得到汽车玻璃曲面展开平面的轮廓，如图6所示.

图6 汽车玻璃曲面展开轮廓图

5 结论

本文提出了曲线映射展开法，此方法展开精度高且易于实现，可适用于非封闭、小曲率、不可分割曲面的展开.汽车玻璃曲面正符合这种曲面几何特点，基于曲线映射展开法，本文开发了汽车玻璃曲面展开系统，并对该系统实现的关键技术进行了研究.展开实例表明，该系统可实现汽车玻璃毛坯的自动生成，对缩短新型汽车玻璃制造周期、降低生产成本能起到积极的推动作用.

［1］刘志国，张永祥 ，简中强.汽车挡风玻璃光学模拟和几何型面优化［J］.汽车零部件，2009(3):32-34.

［2］MANNING JR.Computerized pattern cutting［J］.Computer-Aided Design，1980，12(1):43-47.

［3］陈动之，王国谨.基于伪直母线的复杂曲面自适应分片与展开［J］.软件学报，2003，14(3):660-665.

［4］李基拓.三角化曲面展开技术研究及其应用［D］.浙江:浙江大学，2005.

［5］席平.三维曲面的几何展开［J］.计算机学报，1997，20(4):315-322.

［6］詹雯.复杂曲面展开技术研究［D］.南京:南京航空航天大学，2007.

［7］毛国栋，孙炳楠，徐浩祥.基于弹簧-质点系统的薄膜结构曲面展开算法［J］.浙江大学学报(工版)，2005，39(8):1238-1242.

［8］毛昕，毛普元，孙静.自由曲面近似展开及误差分析系统［J］.机械设计与制造，2007，12:201-203.