连续油管在滚筒上缠绕的力学研究

施志辉，范佳，许立，刘元伟

(大连交通大学 机械工程学院，辽宁 大连 116028)

0 引言

连续油管技术已经成为油气勘探开发领域中一项日益完善的新技术.连续油管技术装备由于其应用范围广被誉为“万能作业装备”［1］，而连续油管的使用寿命是制约整个装备的关键因素.因此，对连续油管在滚筒上塑性变形的力学行为分析很有必要.

国外主要利用实验来进行相关研究，而国内则主要集中于理论分析，包括对连续油管的疲劳、屈曲、挤毁等力学方面进行了一系列的探讨，并取得了一些成果［2-5］.但是，在现场设备的使用过程中，还有许多问题亟待解决.本文在前人的基础上，从工程实际出发，提出了对连续油管在滚筒上塑性变形时力学行为的研究.通过建立力学模型，分析了连续油管塑性变形时的受力，得到了滚筒转矩、油管拉力的计算公式，为连续油管在滚筒上的紧密缠绕与有序收放提供了理论数据.

1 研究条件

连续油管参数［6］:材料80号钢，外径 D=38.1mm，内径d=32.9mm，屈服强度σy=552 MPa，弹性模量E=2.1×105MPa.滚筒参数:轴心直径范围为2 134～3 404mm，在工程实际中，连续油管尽量不要满载，并且油管基于材料本身特性，存在一个卷绕半径极限，超过该值时通过增大卷绕半径的方法来延长连续油管循环寿命无太大意义［7］.取缠绕半径 R=1 200mm，这也与文献［7］中的实验数据相符.

连续油管在纯弯曲状态下的弹性极限半径公式:

将油管参数代入式(1)，得到该类型油管的最小屈服半径Rmin=7 247mm，而缠绕半径R=1 200mm.R远远小于Rmin，所以连续油管在滚筒上缠绕过程中势必发生弹塑性变形.

油管截面上弹性区的半高度计算公式:

2 油管弯曲过程分析

液压马达驱动滚筒旋转，保持对连续油管一定的拉力，把连续油管从油井中抽出，并在滚筒上缠绕起来.油管在从直到弯的过程中，经历了弹性变形到塑性变形的阶段.油管的塑性变形是瞬时发生的，屈服点的位置尚没有标准可循，也不可能准确的定位.故可设定屈服点位置的参数，例如缠绕角度、屈服点离油管缠绕外圈的最短距离等，用来判断油管在滚筒上缠绕的松紧程度.从而通过材料力学分析，推算出合适的油管拉力与滚筒负载，使油管既能够较紧地缠绕在滚筒上，又不至于受力过大导致寿命缩短.故在油管弯曲过程分析中，其重点是在合适负载的条件下实现油管在滚筒上的较紧密地缠绕.取长度L的直管作为研究对象，如图1所示.

图1 油管受拉弯曲力学模型

油管上拉力F产生的内力矩M正是油管塑性变形的原因，根据文献［9］，其弯曲应力等于材料的屈服应力，列出方程得:

根据图1，受力分析可得:

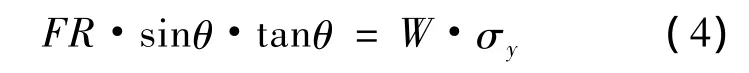
又有:

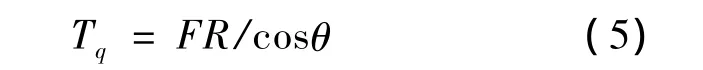
得到关于Tq的计算公式:

式中，Tq是油管从井中起出时滚筒扭矩(N·m);d是直管弯曲变形时屈服点q离油管缠绕外圈的最短距离(mm);W=π(D4－d4)/32D为油管抗弯截面系数，W=2.409 5 ×10－6m3;在计算中，为了简化模型，假设油管上H点紧贴滚筒表面，并且不受竖直力作用.

本文采用屈服点q离油管缠绕外圈的最短距离d来定义油管在滚筒上缠绕的松紧程度.定义d=R/20时，为连续油管缠绕较紧状态.计算可得，连续油管缠绕较紧状态时，滚筒负载扭矩:

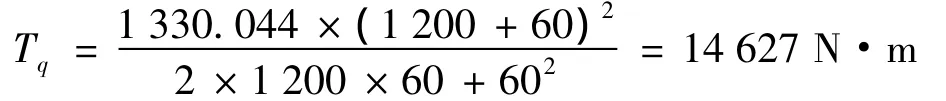
连续油管上拉力:

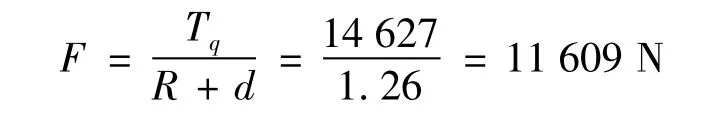
通过工程实践和对注入头等其他连续油管设备的分析，上述所得到的油管拉力远远小于极限拉力，滚筒扭矩也适合大范围马达的选用.因此，可以认为在定义d=R/20的情况下，能够实现油管在滚筒上的较紧密地缠绕，并且得到相关的力与扭矩的数值，具有指导意义.

3 油管拉直过程分析

在连续油管下入油井的过程中，注入头牵引油管从滚筒中拉出，同时驱动马达对滚筒提供一个反扭矩，缠绕好的油管被拉直，油管又经历了一次从弯到直的塑性变形阶段.油管的拉直过程中，不用考虑油管在滚筒上缠绕是否紧密的问题，关键是油管所受的拉力是否合适.

油管在拉直时，张紧程度是一个重要指标，可用松弛角度ψ来表示.随着松弛角度ψ变大，液压马达作用在滚筒负扭矩与油管上的受力都呈减小的趋势.经分析，参数ψ存在一个拐点.在该拐点之前，滚筒负扭矩与油管上受力的减小趋势非常明显，但是具体数值依然很大.较大的负扭矩不利于马达正常运转，同时油管上受力过大影响注入头的工作受力，更严重地降低了油管的使用寿命.在该拐点之后，滚筒负扭矩与油管上受力的减小趋势变化缓慢，扭矩与力均较平稳，滚筒和注入头等设备能够正常地运行.

故在油管拉直过程分析中，重点是选择一个合适的松弛角度ψ，确定相应的油管拉力与滚筒负载，使油管既能被拉直又能不受较大的拉应力，延长使用寿命.取小长度的弯管作为研究对象，如图2所示.

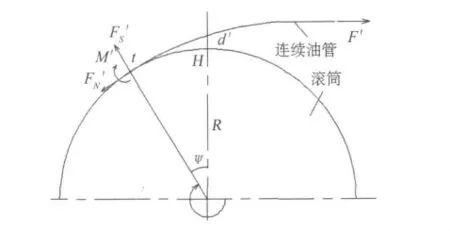
图2 油管受拉变直力学模型

根据图2分析得，连续油管离开滚筒t点时，其横截面上弯矩和轴向力分别为:

滚筒负扭矩可表示为:

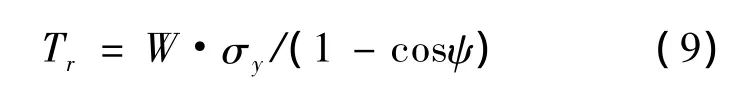
式中，Tr为油管下入油井时滚筒的负扭矩(N·m);ψ是松弛角度;在计算中，为了简化模型，假设油管上H点紧贴滚筒表面，即图2中d'远远小于R，并且在H点不受竖直力作用.ψ和Tr、F'的数值关系，如附表所示.

附表 80号钢连续油管在不同松弛角度下力学参数值

分析可知，松弛角度ψ的拐点值大概在10°左右，取ψ =10°.此时:连续油管上的拉力F'=72 956 N，滚筒负扭矩Tr=87 547 N·m，力和扭矩的数值比较大，工程实际中设备的选用和注入头的极限设计均不允许，故取松弛角度ψ=10°不合适.选择松弛角度ψ =30°，此时:油管上的拉力F'=8 272 N，滚筒上负扭矩Tr=9 927 N·m，小于实际中设备的设计极限，油管既能被拉直又能不受较大的拉应力，延长了使用寿命.但是，松弛角度也不能无限制地增大.虽说随着松弛角度ψ的增大，油管上的拉力和滚筒负扭矩呈减小趋势.随着松弛角度ψ的增大，连续油管与滚筒缠绕表面距离变大，容易乱管.特别当松弛角度ψ≥90°时，油管上拉力F'将变成负值，连续油管上轴向力F'N也变成负值，油管截面受压，油管将不能被拉直，故应该避免该种情况的发生.因此，选择松弛角度ψ=30°是比较合适的.

4 结论

(1)通过力学分析计算，推导出了连续油管在滚筒上缠绕和拉直过程中，滚筒扭矩和油管上受力的相关公式，并给出了较合适的数值，能够满足油管在滚筒上的紧密缠绕和顺利拉出，更为滚筒、注入头等装备理论设计和现场的操作提供了参考;

(2)连续油管在滚筒上的塑性变形是一个复杂的过程，文中力学分析时简化了模型，因此有待于更准确的模型分析.

［1］贺会群.连续油管技术与装备发展综述［J］.石油机械，2006，34(1):1-6.

［2］朱小平.连续油管在弯曲和内压共同作用下的疲劳寿命分析［J］.钻采工艺，2004，27(4):73-75.

［3］朱小平.连续油管卷绕弯曲寿命分析［J］.钻采工艺，2000，23(6):51-53.

［4］王优强，张嗣伟.连续油管的挤毁压力分析［J］.石油矿场机械，1999，28(2):37-40.

［5］赵广慧，梁政.连续油管力学性能研究进展［J］.钻采工艺，2008，31(4):97-101.

［6］李宗田.连续油管技术手册［M］.北京:石油工业出版社，2003:114-115.

［7］王海涛，李相方.连续油管卷曲低周疲劳寿命预测［J］.石油机械，2008，36(11):25-27.

［8］杨高，罗刚.连续管缠绕力学研究［J］.石油矿场机械，2010，39(5):10-13.

［9］刘鸿文.材料力学［M］.北京:高等教育出版社，2004:127-128.