基于风险因子设计的水资源短缺风险评估及预测

于 澜，宋南川，齐 亮，王海峰

（长春工程学院理学院，长春130012）

0 引言

水资源是指可供人类直接利用能够不断更新的天然水体，主要包括陆地上的地表水和地下水。近年来，在我国特别是北方地区水资源短缺问题日趋严重，水资源成为焦点话题。水资源系统风险是由于天然来水的波动、地下水持续保障能力不足、供水条件落后以及水资源社会经济承载负担过重等因素综合作用的结果，对社会、经济、环境存在潜在损害[1]。如何对水资源风险的主要因子进行识别，对风险造成的危害等级进行划分，对不同风险因子采取相应的有效措施来规避风险或减少其造成的危害，这对社会经济的稳定、可持续发展战略的实施具有重要的意义。

本文首先分析了构成水资源短缺的两类风险因子，利用层次分析模型对各风险因子的权重进行了定量分析，并通过风险等级的划分对风险产生进行了定性分析。其次基于风险因子构建了水资源系统风险的评价体系，并采用灰色模型理论，提出了各风险评价指标的预测方法。最后以北京市为例对其水资源短缺风险进行了评估和预测，证实了本文方法的可靠及有效性。

1 风险因素分析

从水资源系统结构来看，风险来源于系统属性和过程对潜在危害的抵抗乏力[2]。一方面由于水资源系统本身的输入主体发生短缺、过程产生波动及输出显示出的脆弱程度等都可能成为导致系统风险产生的重要原因，因此它们是水资源系统风险的致险因子；另一方面水资源系统对致险因子进行反馈，引导系统本身对潜在风险进行抵抗，从而削减风险的产生及危害，我们将这一种反馈及抵抗性质称为承险能力；系统在致险与承险二者相互作用下运行，当致险压力大于承险能力时，风险就产生了。据此风险因子可分为致险因子和承险因子，前者是指引起系统发生变化的因子，包括系统结构的内部变化和外界干扰，而致使风险发生的概率称为致险率，后者则是指系统在充分反馈或经历事故后有能力进行自我调节、自我适应来应对危害的要素，而系统对风险削减的能力称为承险率。

2 基于风险因子设计水资源风险评估体系

为了区分产生缺水现象的主要影响因素，并能有针对性地进行规划和治理，我们采用层次分析法进行定量分析。本文采用层次分析模型（Analytic Hierarchical Model）[3]确定风险因子的权重，其主要步骤如下：

（1）根据1～9标度理论构造判断矩阵A＝（aij）n×n 。

（2）根据转换公式构造AHM的测度判断矩阵B＝ （uij）n×n，并逐行进行一致性检验。

（3）将测度判断矩阵B的每一列正则化：

（4）求出判断矩阵B的每一行各元素之和：

（5）将对应向量正则化：

本文中准则D＝（D1，…，Dn）T确定为各风险因子，其中[1]：

需要说明的是，第（2）条是AHM的核心环节，即将比例标度判断矩阵A转换为测度判断矩阵B，转换公式为 ：

式中，aij是按照1～9标度理论得出的第i项较第j项的相对重要值，本文在实例计算过程中认为取β＝2比较合理。

下面设计5种风险指标来建立水资源系统风险评价体系。首先通过构建综合风险损害指标DI来表示风险发生时对系统的破坏程度[4]，如下式所示：

其中体现致险因子和承险因子对系统作用程度的致险率（RBI）及承险率（RSI）分别计算如下：

式中：m和n——为致险因子和承险因子的个数；

Ri——系统各风险因子的指标值，记¯R＝（R1，…，Rm＋n）T，它们的确立可参考文献[1]中的方法；

ωDi——系统风险因子对于系统的贡献大小，构成系统风险的权重向量ωD（见式（4））。

水资源系统脆弱性指标（CI）既包含引起风险发生的致险因子，又能反映水资源系统的受损害程度

式中：k～l——指系统发生风险时能体现出社会、经济损失及生态损害的那部分风险因子的标号；

ωs——表示系统风险的发生及传递对系统损害率在相关评价指标体系上的指标权重的重分配值，可参见文献[1]。

通过推证可知，采用

水资源风险评价体系构建完成后，参考美国军用标准 MIL－STD－882[5]《系统安全程序的系统和相关的系统及设备》中提供的定性分析方法，在充分考虑系统的致险因子与承险因子的相互关系后，可将水资源系统风险划分为5级，以表征不同的风险级别，并可采用相应的抗险措施，见表1。

表1 水资源系统风险级别

3 基于GM（1，1）模型的水资源风险趋势预测

灰色数列模型是以时间序列进行研究分析，用数列建立方程，将无规律的原始数列经过转换，使之成为较有规律的生成数列后再建模的一种预测方法，可以从实践工作经验、实际数据特征、时间序列图形、预测误差比较等多方面进行综合分析。其中，较为简单的一种模型——采用一个变量的一阶微分方程GM （1，1）模型[6]已经广泛应用于医学等研究的许多领域之中。下面我们运用GM（1，1）模型对水资源风险趋势进行预测。

建立某一水资源风险指标的原始数据时间序列：

其中，X（0）（n）可定义为2010年的数据，通过

将原始数据进行一次累加生成新序列：

建立GM（1，1）模型相应的微分方程为：

式中：α——发展灰数；

μ——内生控制灰数。

其中

求解微分方程式（11），即可得预测模型：

用式（12）计算X（1）（k），然后由关系式

可得到某一待估风险指标的原始数据序列X（0）（k＋1）（k≥n）的预测值。

4 实例分析

根据2001年—2009年北京市水资源公报显示的数据资料，我们提取了20个影响水资源的因素，并根据这些因素对缺水风险的贡献，把其中14个作为致险因子，其中包括缺水率D1，缺水量波动性D6，超采量D3等等，还有6个因素作为承险因子，例如水资源量保障程度D15和非常规水资源D16等等。结合北京市水资源系统状况，得到北京市2001年—2009年风险指标值¯R及权重值ωs和ωD，利用式（8）、式（9）、式（10）、式（7）得到北京市水资源系统的致险率（RBI）、承险率（RSI）、脆弱性（CI）、风险（ωD¯R）、风险损害（DI）分别为57.63%、40.05%、42.46% 、27.3%、7.46% 。结果显示北京市面临27.3% 的风险，并将会导致系统7.46% 的风险损害，这也是风险发生对系统的破坏程度。据水资源系统风险级别表（表1），北京市水资源风险处于II级风险阶段。

根据 GM （1，1）模型的预测方程（12）和（13），可分别预测出2011和2012年度的致险率（RBI）、承险率（RSI）、脆弱性（CI）、风险（ωD¯R）及风险损失（DI）指标，见表2。

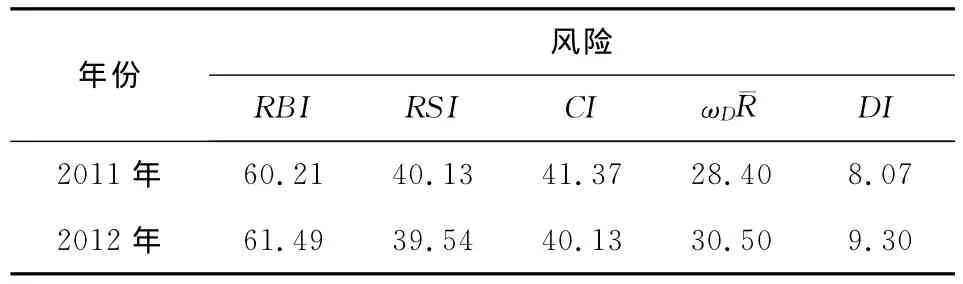
表2 2011、2012年风险评价指标的预测值／%

从上表可以得出结论：在未来两年北京市水资源短缺风险正在呈上升趋势，但基本还处在可约束的风险级别内，所以我们还是要通过控制水资源的使用来防范风险，通过推进高效的水资源系统管理体制和优化配置水资源等来促进水资源系统的恢复，从而有效地控制风险发生并去除其潜在损害。

[1]张士峰，陈俊旭.水资源系统风险构成及其评价—以北京市 为 例 [J].自 然 资 源 学 报，2010，25（11）：1855－1863.

[2]杨士尧.系统科学导论[M].北京：农业出版社，1986：390－410.

[3]朱发昇，董增川.基于AHM方法的石羊河流域缺水影响因子分析[J].人民黄河，2007，29（12）：47－48.

[4]Tobin G A，Montz B E.Natural Hazards Explanation and Integration[M].New York：The Guilford Press，1997：1323－1367.

[5]MIL－STD－882，System Safety Program for system and Associated Subsystems and Equipment[S].

[6]吉培荣，黄巍松.无偏灰色预测模型[J].系统工程与电子技术，2000，22（6）：6－7.