竹材模型结构底部滚球与顶部TLD 联合减震公式推导

常伏德，张晓玉，丁 睿，王仲启

（长春工程学院土木工程学院，长春130012）

0 引言

隔震是结构振动控制中研究最早、应用最广的一项减震技术。它的基本原理在于通过设置隔震装置使得结构体系的水平刚度降低，使其自振周期延长，远离上部结构的自振周期和场地卓越周期，从而把地面运动有效地隔离开来，达到减震的效果。基础隔震是在上部结构和基础之间设置隔震层，通过隔震层的隔震系统来限制和吸收传入结构的地震能量。对竹材模型结构，赛题规定顶部必须采用TLD减震方式，在此基础上我们提出了底部采用滚球隔震，形成一种联合减震方案，给出了体系运动微分方程，并给出了底部输入给结构的加速度即滚球形心的加速度公式推导，并推导了滚球等效支承的模型公式。

1 结构体系耦联运动微分方程

竹材模型结构底部滚球与顶部TLD减震模型如图1所示。

由文献[1]和文献[2]结构体系藕联运动方程下：

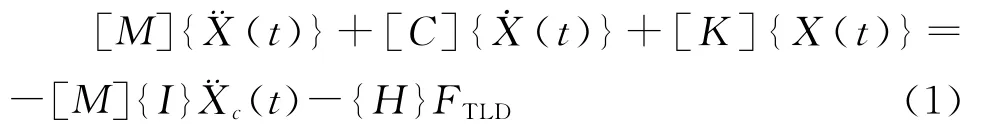
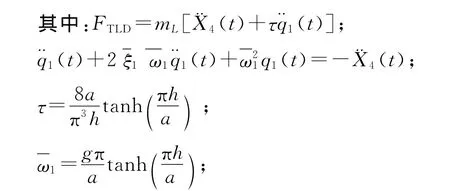
｛X（t）｝——结构层对地面（台面）的层位移；

[M]——结构质量矩阵；

[C]——结构阻尼矩阵；

[K]——结构刚度矩阵；

｛I｝——单位列向量；

｛H｝＝[0 0 0 1]T——TLD设置矩阵；

FTLD——顶部水箱对结构的控制力；

q1（t）——水箱水晃动第一振型反应位移；

ξ1——水晃动第一振型阻尼比；

mL——水箱质量；

h——水箱里的水深；

a——水箱宽度。

2 滚球形心水平加速度（t）的公式推导

（1）滚球的运动分析：图2为滚球运动分析图，设滚球纯滚动，滚球运动是牵连运动为平动的复合运动。

图2 滚球运动分析图

由图2知道，假设滚球仅做微小运动，则

（2）滚球的受力分析：滚球受力分析如图3所示，图中各力说明如下：

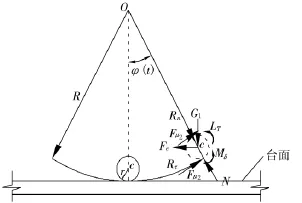
图3 滚球受力分析图

G1为一个小球承受的荷载重力；N为球面支撑力；Fμ1为台面给球的静摩擦力，Fμ2为上部结构给球的静摩擦力。设滚球与上下接触部位的材料相同，则Fμ1≈Fμ2；Mδ为滚球滚动摩阻力偶矩，计算式为Mδ＝Nδ，δ为滚动摩阻系数，因N≈G1则 Mδ＝G1δ；Rτ为切向惯性力：

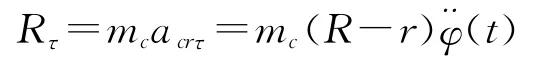
mc为小球质量；Rn为法向惯性力：Rn＝mcacrn；Fe为牵连加速度引起的水平惯性力为小球转动惯性力矩为小球滚动角加速度则由图3对球心C取矩即∑Mc（F）＝0得：

将Mδ，LT及Fμ1≈Fμ2代入式（4）整理得：

将式（5）代入式（3）整理得：

3 滚球等效支承刚度推导

滚球在球面上的受力如图4所示（此处略去摩擦的影响），图中几何关系有

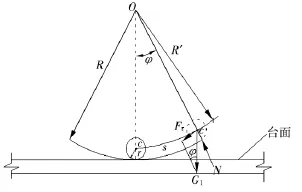
图4 滚球等效支承刚度推导图

球面对滚球的支撑刚度可用切向刚度kτ和法向刚度kn来描述，假设球面支撑为刚性，则法向刚度kn＝∞，下面进行切向刚度kτ的推导。

上部结构通过柱子传给滚球的重力G1的切向分力Fτ即为滚球的恢复力，切向刚度kτ实质就是切向分力Fτ对弧长s的偏导数。

由图4知道Fτ＝G1sinφ，又则切向刚度kτ为：

当滚球做微小滚动时，cosφ≈1，则

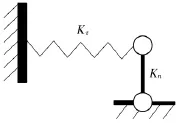
图5 滚球等效支撑图

4 结语

（1）由式（6）知道，滚球隔震减少了对结构的输入加速度，根据需要可调整滚球半径、质量、摩阻系数等，可以使输入加速度减小到理想值；

（3）有关的理论推导对其他结构减震分析及应用也有一定的指导意义。

[1]翟伟廉.高层建筑和高耸结构的风振控制设计[M].武汉：测绘科技大学出版社，1991：180－181.

[2]郭婷，何玉敖.新型水箱减震控制系统TLMD的分析研究[A].中国建筑学会抗震防灾研究会，中国地震学会地震工程专业委员会.第五届全国地震工程会议论文集（Ⅱ）[C].北京：[s.n.]，1998：857－862.