一种模拟三维红细胞变形的前向跟踪式格子Boltzmann方法

杨 婷 魏守水 崔建强

(山东大学控制科学与工程学院，济南 250061)

引言

血管病变可以引发许多人体疾病，且病例逐年增加，血管病变及血流运动的研究成为近20年科研的重点。红细胞在血液中所占的百分比最大，被认为是影响血液流动的主要因素，它在血管中的运动特性也引起了人们的关注。

红细胞是双凹碟状，其内充满液体［1］。将红细胞模拟为内含黏质牛顿流体的、由不可压缩弹性薄膜构成的双凹碟形胶囊，此类胶囊模型已用于生物细胞、脂质囊泡等的研究［2］。在分子生物学、生物工程学和化学工程学领域，已有许多研究者涉及过此类胶囊在流体驱动下的变形研究。对于脑疟疾和镰状细胞性贫血等血液疾病，红细胞失去了变形的能力，变硬的薄膜导致其经常堵塞在毛细血管中。为了找出类似疾病的临床治疗方法，了解在流体中界面机械特性如何影响细胞的变形行为是非常必要的，而且这也是模拟更加复杂情况(比如人类微循环、细胞筛选、药物传递等)的基础。

在目前的研究方法中，数值计算可以弥补理论分析和实验研究的不足，对复杂的流体力学问题进行既快又省的计算分析，因此在流体驱动变形胶囊式红细胞的研究中引起了人们的关注。

任意角度的拉格朗日欧拉方法(ALE)是一种直接处理流固耦合的方法［3］。流体区域的边界随着流固耦合的运动而移动，且网格随之重建。ALE方法具有高准确度的优点，但是计算量较大。对于具有复杂几何结构或者大变形性的红细胞模型，重组网格过程是非常困难的。边界元方法(BEM)最成功的应用是研究蠕动流中的胶囊变形［4－7］，控制方程只需建立在模型界面上，因此问题的几何维数可以减少到一维。Peskin等提出浸溶边界方法(IBM)，用以模拟心脏的血液流动［8］。在这种方法中，为了计算边界的影响，移动边界附近的力密度分布在一个笛卡尔网格上，力密度由边界本构方程计算得到。IBM适合模拟流固耦合问题，Eggleto等用此方法研究了剪切流中三维胶囊的大变形［9］。但是，单独使用此方法，计算负荷过大。

经过多年的发展，晶格波尔兹曼方法(LBM)已经成为一种极具前景的数值方法，尤其是在模拟包含表面动力学特性和复杂边界情况的流体运动方面［10］。LBM基于微观模型和介观动力学方程，与传统的基于宏观连续性方程离散化的数值方法有很大不同。使用宏观流体运动的简化动力学方法的基本前提是:流体运动的宏观动力学特性是无数微观粒子集体行为的结果。相比传统的流体力学计算方法，在处理复杂固体或自由边界条件时，LBM有很多优势。但是，单纯使用LBM，模型很难适用于特定膜结构的系统，特别是当细胞直径只占少数晶格单位的时候，薄膜轮廓粗糙，影响了计算准确度。

IBM方法与晶格波尔兹曼方法相结合，形成了一种基于动力学的方法来模拟流体流动［11］。Feng等用这种方法来研究颗粒流动［12］。Peng等比较了在LBM方程中流固情况下的浸溶边界法和内插反弹边界法，结果发现IBM实施起来更加容易，但是准确性较低［13］。在标准 LBM方法中，使用的是统一的笛卡尔网格，这使得在大领域计算过程中方法的效率降低。文献［14-15］使用了多块LBM进行改善，计算领域被分成了多块:大梯度处使用细网格，其他处使用粗网格。通过多块策略，LBM的计算效率得到了实质性的改善。Peng等应用多块策略的浸溶边界式晶格波尔兹曼方法(IB-LBM)，研究了二维情况下静态固体边界中的流动［16］。文献［17］结合了同样的方法，研究在流体中变形的二维胶囊的瞬态行为。在二维和三维的情况下，流体驱动下的胶囊变形行为存在有很大的不同:三维数值模拟会加大计算量，考虑更多的影响因素，更加贴近实际过程，也更加复杂。文献［18］将 IB-LBM方法扩展到三维，包含了有限元薄膜模型，用来计算薄膜力，并且研究了剪切流中三维胶囊的瞬态变形。但该方法的局限，在于胶囊模型内部的液体必须与外部液体具有同样的物理特性。

近年来，由 Tryggvason等提出前向跟踪方法［19］，在界面动力学的数值模拟中显现出它的优越性。前向跟踪方法与浸溶边界法有很多相似之处，比如为计算边界的影响，将移动边界周围的力密度分布在笛卡尔网格上。前向跟踪方法的优势，在于液滴或者胶囊式细胞内外的物理特性可以是不同的。在前向跟踪方法中，可将液滴或胶囊模型内外不同的液体看做是具有不同物理特性的流体［20］。另外，前向跟踪方法已经用来研究二维液滴［21］和细胞［22］，以及三维胶囊［23］在流体驱动下的变形行为。Lallemand等将LBM和前向跟踪法相结合，研究二维中具有表面拉力的变形表面的动力学特性［24］。

本研究将前向跟踪方法与LBM方程相结合，研究流体驱动的三维红细胞的变形。与混合方法［17］对比，改善之处在于包含了一个指标函数，以消除先前研究中模型内外的液体必须具有同样黏度的限制。双凹蝶形胶囊式红细胞内外的流质被看做是具有不同物理特性的液体，细胞薄膜通过匀速运动的薄膜点清晰地单独跟踪。细胞薄膜离散为松散的平面三角形元素，并可以计算薄膜机械力。采用多块LBM策略，在细胞附近的领域使用细网格划分，所以在三维计算中计算准确性和效率都得到了较大提高。通过研究简单剪切流，在多种无因次剪切率和黏度比下，出现了具有Skalak薄膜本构法的双凹蝶形胶囊模型的变形行为，证实了本方法的有效性。

1 双凹碟形薄膜模型

1.1 薄膜的本构方程

在描述薄膜特性的多种本构法中，采用了由Skalak等提出的本构方程，即专门用来模拟红细胞薄膜的 Skalak 法则(SK)［25］，有

式中，WSK为Skalak法则下的应变能;式右侧第一项为剪切效应，相应模量为E，第二项为区域膨胀，相应模量为CE;I1和I2分别为第一个和第二个应变量，I1=－2，I2=(λ1λ2)2－1，项 λ1和 λ2分别原始应变常量。

1.2 薄膜离散化

将三维胶囊式红细胞模型的薄膜离散为许多平面三角元，三角化过程类似于文献［4］所述。对于双凹圆盘，即静态红细胞形状，测绘系统方程为

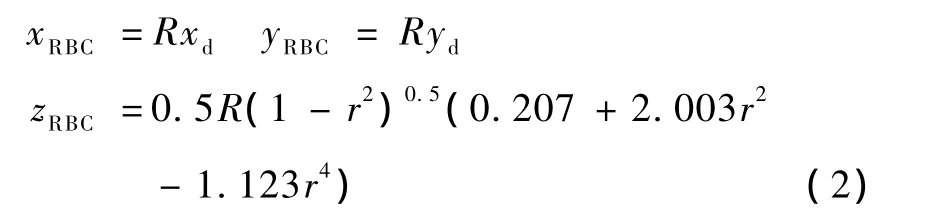
式中，xd和yd分别为自定义的红细胞长短轴长度，r2=，zd为自定义高度，详见文献［4］，R 是为保持细胞模型体积不变的调整因数。

离散化的双凹碟形表面如图1所示。

一种有限元薄膜模型被用来获得作用在薄膜离散点上的力，详细的处理方法可以参看文献［25］。

图1 离散化的双凹蝶形表面。(a)面离散图;(b)4个方向上的立体图Fig.1 Discretization of a biconcave disk shape.(a)surface discrete figure;(b)stereo on four directions

2 数值方法

结合前向跟踪法和晶格波尔兹曼方法，模拟三维双凹碟形胶囊式红细胞在流体驱动下的变形行为。在LBM架构中引进前向跟踪技术，有助于更好地描述薄膜特性;红细胞薄膜通过匀速运动的薄膜点清晰地跟踪，细胞薄膜离散为平面三角形元素，使用上述模型计算薄膜机械力;使用多块LBM策略改善红细胞模型附近的网格，从而提高了计算准确度和效率。

红细胞模型剖面如图2所示，它的边界为Γ，内部液体为Ω1，浸溶在液体 Ω2里。整个流体区域由欧拉坐标x表示，红细胞边界Γ由拉格朗日坐标s表示。

首先，使用前向跟踪法研究红细胞薄膜。薄膜力密度Ff(s，t)可以通过文中1.2节讨论过的有限元薄膜模型获得，并分布在附近的流体网格点上，有

式中，ff(x，t)为使用前向跟踪法获得的流体体积力密度，Ff(s，t)为由此方法获得的红细胞变形产生的薄膜力密度，X(s，t)为薄膜上的任一位置，δ(x－X(s，t))为狄拉克函数的一种平滑估计。

在三维研究中，选定为

图2 浸溶在笛卡尔网格中的薄膜离散为拉格朗日点的模型Fig.2 Illustration of a red blood cell whose membrane is divided into Lagrangian points immersed in a Cartesian grid

同样，估计函数可以用来获得移动边界上拉格朗日点的速度。为了满足无滑移边界的情况，令弹性薄膜与周围流体的运动速度相同，其数学形式为

红细胞内速度 μ(x，t)=μi，且 Ω =Ω1;细胞外速度 μ(x，t)=μo，且 Ω =Ω2。随着红细胞移动和变形，它在流体场中的物理特性需要随之更新，更新的方法详见文献［13］。

其次，解决流场问题时可结合晶格波尔兹曼方法。为了解决含有力密度的流体场，必须改良晶格波尔兹曼方程。晶格波尔兹曼方法是一种模拟流体流动的动力学方法［11］，它将连续性流体分散为流体颗粒块，这种颗粒只能静止，或者移动到相邻点上。考虑到实际运动情况，使用常见的D3Q19模型(见图3)作为三维模型，其离散晶格波尔兹曼方程为

式中，fi(x，t)为t时刻、速度矢量为ei的粒子在x位置上的分布函数，Δt为晶格的时间间隔，feqi(x，t)为平衡分布函数，τ弛豫时间，i=0，1，…，18。

图3 D3Q19模型Fig.3 D3Q19 model

在D3Q19模型中，流体颗粒可能的离散分布速度为

为计算力密度，离散晶格波尔兹曼方程被修改为

相应的平衡分布函数为

式中，ωi为权重因数(i=0，1，…，18)。当 i=0 时为1/3，i=1～6时为 1/18，i=7～18时为 1/36;cs为声速，其值为 Δx/(Δt);I为更新物理特性时使用的矢量函数，详见文献［13］。

在纳维斯托克斯方程中，弛豫时间与运动黏度相关

一旦知道粒子分布密度，流体密度和动量都可以从计算获得，有

同时，采用多块LBM，使计算领域分块，块之间通过接触面连接在一起，块间的表面上变量交换遵循一定的关系，以保证质量和动量守恒、接触面上的压力连续。图4为两块间的界面典型结构，为了便于信息交换，细块边界MN在粗块的内部，粗块边界AB在细块的内部，MN和AB代表垂直于纸面的位面。在图4中，细网格边界MN上的黑点无信息，它们是基于白点上的信息、通过空间内插获得的。采用二维立方样条曲线的空间拟合，详见文献［15］。因为每块中的流体颗粒拥有相同的流速，计算边界区域细网格上的是粗网格上的m倍。在细网格块边界MN上，为了获得碰撞后的密度分布函数，需要进行瞬时内插，内插使用三点拉格朗日方法。

图4 两块间界面结构Fig.4 Interface structure between two blocks

计算时采用了二坐标制系统，粗细格子间的晶格空间比率是2，红细胞浸溶在细网格块中。多块计算的流程与文献［15］中的方法类似，两者的区别在于本研究进行细网格计算时利用了前向跟踪方法。

3 分析方法

为验证当前方法的有效性，分析了惯性力对模型变形的作用，并模拟了简单剪切流中Skalak薄膜包裹的双凹碟形胶囊模型的稳定坦克履行为，剖面如图5所示。

在初始状态时，模型无应力。在模型变形过程中，多个无量纲参数起到了决定性的作用，包括无因次剪切率、黏度比和雷诺数。无因次剪切率G=μoka/E，其中 μo是周围流体的黏度，k是剪切率，a是模型的初始半径，E是模型薄膜的剪切弹性。黏度比λ=μi/μo，其中μi是模型内部流体的黏度。双凹蝶形胶囊模型半径a为长度尺度，选定ka为速度尺度，1/k是时间尺度。雷诺数 Re=ρ(ka)a/μ，其中ρ是周围流体的密度。

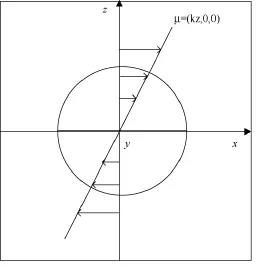
图5 剪切流中模型剖面Fig.5 Section of a model in simple shear flow with plane of shear

3.1 计算区域和网格分辨率分析

首先，研究无边界剪切流中Skalak薄膜双凹碟形胶囊式红细胞模型的网格分辨率和计算区域的敛散性。类似于文献［6］，在式(1)中，选定常数比率C=1。雷诺数为0.025。

为了忽略边界影响，计算领域必须足够大，同时网格分辨率足够高。在多种尺寸的计算领域和多种网格分辨率下，进行数值模拟。指标参数是红细胞的泰勒形状参数 Dxz，它定义为 Dxz=(L－B)/(L+B)，其中L和B分别是剪切面上红细胞的长轴半径和短轴半径［6］。泰勒形状参数越平缓，则表明计算墙密闭效应的影响越小。

计算区域是一个立方盒子。红细胞模型位于立方体中心，它的薄膜离散为8 192个三角元，连接着4 098个点。细网格覆盖一个较小的立方盒区域，其边长为4a，中心与计算区域的中心重合。其他区域均使用粗网格，网格分辨率分别为Δxf=Δyf=Δzf=a/12，Δxc=Δyc=Δzc=a/6。计算区域外边界分别设为8a、10a、12a，外边界情况为无扰动的简单剪切流。

3.2 惯性作用分析

惯性是有量物体的一种固有属性。研究主体是线性剪切流中具有Skalak薄膜的双凹面形胶囊式红细胞模型，现在还没有人研究在三维内部充满流体的弹性薄膜红细胞模型的变形中惯性产生的作用。

两个向相反方向移动的固体墙产生线性剪切流。计算领域是一个长8a的立方盒，红细胞模型位于区域的中心。计算区域上下平面的边界设置为相反方向移动的固体墙，另4个面使用周期边界情况。当雷诺数Re=0.025～2.5时，每个轴上的2a～6a处覆盖细网格。粗细格的网格分辨率和薄膜离散化程度与前相同。当雷诺数Re=10～25时，细网格覆盖每个轴上1.5a～6.5a的区域，网格分辨率为 Δxc=Δyc=Δzc=a/8，Δxf=Δyf=Δzf=a/16。薄膜离散为32 768个平面三角元素，连接16 386个点。

3.3 坦克履行为分析

在红细胞获得稳态后，其薄膜会围绕内部流体开始旋转，这就是著名的可减少流阻的坦克履行为。但是，由于红细胞复杂的几何结构，所以以往的计算中都出现过数值不稳定性，坦克履行为只维持了较短的阶段［26］。目前，数值模拟还没有完全复原三维双凹碟形红细胞的坦克履行为。

研究范围从0.025～0.2的无因次剪切率G下，黏度比λ=0.2或5时红细胞模型的变形。基本网格参数本文同3.1。当模拟λ=0.2时，细胞的行为时，弛豫参数τ在粗网格块处的值为0.716，在细胞外细网格处为0.932，细胞内部为0.586;λ=5时，弛豫参数分别为0.554，0.608和1.04。采用Skalak法则来描述薄膜机械特性。

4 结果与分析

使用前述实验方法，分析了惯性力对模型变形的作用，并模拟了简单剪切流中Skalak薄膜包裹的双凹碟形胶囊模型360°的稳定坦克履行为。

4.1 计算区域和网格分辨率的确定

首先研究无边界剪切流中Skalak薄膜双凹碟形胶囊式红细胞模型的网格分辨率和计算区域敛散性。如本文3.1所述，在式(1)中，选定常数比率C=1。雷诺数为0.025。

在多种领域尺寸下，在G=0.05、λ=0.2和λ=5时，泰勒形状参数的瞬时变化如图6(a)和(b)所示。由文中3.1知，选用作为时间尺度，为了便于计算，对时间进行了归一化处理，均选用 kt作为横轴。当计算区域的尺寸很小时，墙产生的强密闭效应极大地增加了红细胞模型的变形。随着黏度比的增加，这个作用似乎更加明显。类似的现象在文献［26］中亦有描述。在图6中，同样可以观察到，立方体计算区域边长为10 a时，基本可以忽略强边界密闭效应。

图6 当G=0.2、λ取值不同时模型泰勒形状参数的变化。(a)λ=0.2;(b)λ=5Fig.6 Evolution of the model’s Taylor shape parameter when G=0.2 and λ was choser different values。(a)λ=0.2;(b)λ=5

综上所述，选择边界为10a的计算区域来研究网格收敛性。外围直径为2a的细胞模型被格档分别为20、24或32的细网格块覆盖。在最细的网格处，细胞薄膜被划分为连接16 386个点的32 768个平面三角元。G=0.05，λ=0.2时，4种网格分辨率下泰勒形状参数的瞬时变化如图7所示。图7中右上角的数字依次代表粗网格分辨率、细网格分辨率及细胞薄膜被离散的三角元数。从结果中可以清楚地看到，分辨率为 Δxf=Δyf=Δzf=a/12的网格，离散为连接4 098个点的8 192个三角元的细胞模型薄膜，对于获得重要的特征是有效的。因此在本研究中，所有的模拟均使用此计算区域和网格分辨率。

图7 当G=0.05，λ=0.2时多种网格分辨率下模型泰勒形状参数的变化Fig.7 Evolution ofthemodel’sTaylor shape parameter at G=0.05，λ =0.2 under various mesh resolutions

在保证相同的模型和剪切率下，另外一种模拟方法使用统一的网格分辨率 Δxf=Δyf=Δzf=a/12覆盖整个计算区域。在这种模拟中可以发现，泰勒形状参数的瞬时变化曲线(见图7)和目前的多块FT-LBM方法基本一致。在本研究中，细网格仅覆盖了每个轴的40%，即整个三维计算区域的6.4%，从而大大节省了计算费用和时间。同时可以看出，随着剪切率的增加，细胞趋于与流体方向一致。

4.2 惯性作用

研究对象是惯性作用，研究主体是线性剪切流中具有Skalak薄膜的双凹面形胶囊式红细胞模型。

图8和图9分别显示了雷诺数在0.025～25范围内、λ=0.2时，G=0.05和 G=0.1处红细胞模型的泰勒形状参数和倾斜角度的瞬态变化。有趣的是，在中等雷诺数时、在红细胞模型达到稳态前，由于惯性作用，会产生一个瞬变过程，这种现象在雷诺数更高的情况下尤其明显。而无雷诺数作用的简单剪切流变形的胶囊式红细胞模型，其变形过程是平滑变化的。在瞬变时期，泰勒形状参数和模型倾斜角度是缓冲震荡的。由惯性导致的类似的瞬变过程，同样出现在 Lee和Pozrikidis［27］液体滴的数值研究中，这也间接证明了本方法的有效性。

图8 当λ=0.2，G=0.05时多种雷诺数下Skalak薄膜红细胞模型的瞬态变化。(a)泰勒形状参数变化;(b)倾斜角度变化Fig.8 Instantaneous changes schemes of red blood cell models with Skalak membrane when λ=0.2 and G=0.05。(a)Taylor shape parameter;(b)Inclination angle changes

在瞬变期后，红细胞胶囊模型达到稳定状态。通过比较不同雷诺数下的泰勒形状参数，可以发现惯性作用推动了细胞的变形。将Re=0.25与Re=0.025时的曲线相比，同样可以看到，直到 Re=0.25，惯性作用对红细胞变形影响都很小。

惯性作用可增加模型变形，它同样诱发了一个初始的瞬变过程，即红细胞模型的形状和倾斜角在较大雷诺数时出现缓冲震荡。因此，对于在同样剪切率下的双凹碟形胶囊式红细胞模型而言，较大雷诺数时惯性作用下模型获得稳态的时间要长。图8和图9中的计算在获得稳态后即很快停止。

4.3 稳定的坦克履行为

模拟结果显示，在浸溶到剪切流中后，红细胞在流体剪切力下，均朝着一个稳定的形状和角度开始变形。在G=0.05、λ=0.2时，单个三维红细胞的变形过程如图10所示。本模型考虑了惯性作用，但是由于雷诺数只有0.025，惯性作用可以忽略。

图9 当λ=0.2、G=0.1时多种雷诺数下Skalak薄膜红细胞模型的瞬态变化。(a)泰勒形状参数变化;(b)倾斜角度变化Fig.9 Instantaneous changes schemes of red blood cell models with Skalak membrane when λ=0.2 and G=0.1。(a)Taylor shape parameter changes;(b)Inclination angle changes

图10 当G=0.05、λ=0.2时，无量纲时间kt=0～5处(即坦克履行为半个周期内)双凹碟形胶囊式红细胞三维模型(薄膜上的12个圆点用来标记薄膜路径，小箭头表示时间顺序按逆时针排列，上下粗箭头表示处于剪切流中)Fig.10 3D tank-treading motion of a biconcave discoid erythrocyte model for a half rotation when G=0.05，λ =0.2，at dimensionless timekt=0～5(Twelve material points on the membrane(small spheres)serve as markers of membrane motion;The small arrows show that chronological order is anticlockwise，and the coarse arrows upper and down denote that they are in shear flow)

从图10中可以清晰地观察到红细胞的坦克履行为。整个薄膜处于稳定的双凹碟形中，红细胞的变形并不明显。薄膜上的12个圆点是标记，显示的是12个拉格朗日质点，可以发现这些质点是在旋转的。标记点的路径基本是平行的，从中心凹陷部分到外沿边界的过度始终是平滑的。当红细胞达到稳态形状时，由平面剪切变形产生的弹性行为可以解释这一现象。在旋转一圈(360°)后，标记点将回到初始位置附近。图11明晰地显示，当G=0.05、λ=0.2时，剪切面中达到稳态的红细胞横截面周围的流线。由于红细胞获得了稳态，并开始了坦克履行为，在严格满足无滑移边界的情况下，红细胞横截面将成为一个完美的闭合流线。将图11上图放大，可以发现横截面附近的流线与细胞表面并不是非常贴合。这表明，使用当前的FT-LBM方法，无法严格地保证无滑移边界条件。但是，薄膜速度的横向部分相对于切向部分是可以忽略的，所以在相当长的一段时间内，红细胞仍能够以一种稳定形状保持坦克履行为。

5 讨论和结论

图11 当G=0.05、λ=0.2时，剪切面上稳态红细胞模型横截面周围的流线(内侧粗线代表红细胞薄膜)Fig.11 Streamlines around the cross-section of steady-state red blood cell model in the shear plane when G=0.05，λ =0.2(The inner bold solid line represents the cell membrane)

本研究提出了一种粗细网格结合的思路，即多块LBM策略，使细网格仅占计算区域的6.4%，同时将细胞薄膜离散为连接4 098个点的8 192个三角元，与使用统一网格的方法相比［6，24］，在提高计算效率的同时，节省了计算时间。从图6中可以看到，当边界大于10倍细胞边长时，可以忽略边界影响。这里为了便于计算，仅取了整数值，在以后的研究中，可以考虑非整数值边界的效果。这种思路是以数值建模为基础，利用有限元模型，所以更加合理地划分网格，建立与实际更加接近的模型，会使计算结果更加精确。在建模过程中，虽然考虑到红细胞薄膜内外的流体具有不一样的性质，但是仍默认细胞内外没有物质交换。如何将细胞间的物质交换进行数值建模，将是未来工作的重点之一。

分析了惯性对于模型的变形过程和稳定形状的影响以及对流场的作用，发现在雷诺数不大于0.25时，可以忽略惯性对细胞变形的影响。在研究中可以看到，在较大雷诺数和惯性的作用下，细胞会产生一个瞬变运动。由于在本研究的红细胞运动中雷诺数都很小，所以没有对这种瞬变运动做过多研究。可以在一般的悬浮粒子的液体等固液两相流动情况中进一步讨论。

同时，研究了三维双凹蝶形红细胞的运动，得到了与实际健康红细胞运动及其类似的一个周期的稳定坦克履行为。由于首先研究了计算区域、网格分辨率和惯性作用，所以相对于原先使用同一网格的浸溶边界式晶格波尔兹曼方法［12－13］，计算效率和准确度都得到了提高。新提出的方法是Lallenmand等人工作从二维到三维的一种延伸［24］，与2008年提出的另一种混合方法相比［18］，消除了坦克履运动时红细胞模型内外的流体必须拥有同样性质的限制。可惜的是，本方法模拟的坦克履运动无法严格地保证无滑移边界条件，这主要是由于前向跟踪方法的跟踪性造成的。但是，薄膜的横向速度相对于切向速度是可以忽略的，这也是仍然应用FT-LBM进行红细胞研究的原因。

笔者提出了前向跟踪法与LBM相结合的方法，研究流体驱动下充满流体的三维双凹碟形胶囊式红细胞的变形行为。红细胞模型内外为具有不同物理特性的流体，双凹碟形胶囊模型的薄膜离散为平面三角元，被流体匀速输送的薄膜点可以清晰地追踪薄膜的行为。

使用本研究所提出的方法，首次分析了惯性对于红细胞模型运动状态的影响以及对流场的作用，理论证明了在健康红细胞运动中可以忽略惯性的作用;同时，成功应用数值方法，模拟出了三维红细胞的360°稳定坦克履行为。

目前的三维方法不仅由于使用多块LBM策略，使细网格仅占每个计算轴的40%，从而增加了方法的效率，而且使用了有限元模型来计算三维弹性薄膜的机械能，与以往的类似方法相比，消除了模型内外的流体必须拥有同样性质的限制。

本研究仅限于单个健康红细胞的运动形态分析，且忽略了细胞薄膜模型内外流体之间的相互作用，因此在以后的工作中，在下一步的研究中，可定量地考虑细胞间作用力对红细胞变形和运动的影响，并进一步研究病态红细胞的变形运动，亦可将该方法推广至其他固液两相流的情况中进行讨论。

［1］郭尚平.脏器渗流多孔介质的物理特性［J］.力学学报，1982，13(1):26－33.

［2］Fung YC.Biomechanics:Mechanical properties of living tissues［M］.(2ndEdition).New York:Springer，1982，9:788－789.

［3］Yue Pengtao，Feng JJ，Bertelo CA，Hu HH.An arbitrary Lagrangian-Eulerian method for simulating bubble growth in polymer foaming［J］.Comput Phys，2007，226:2229 －2249.

［4］Pozrikidis C.Finite deformation of liquid capsules enclosed by elastic membranes in simple shear flow［J］.Fluid Mech，1995，297:123－152.

［5］Ramanujan S，Pozrikidis C.Deformation of liquid capsules enclosed by elastic membranes in simple shear flow:Large deformations and the effect of capsule viscosity［J］.Fluid Mech，1998，361:117－143.

［6］Lac E，Barthes-Biesel D，Pelekasis DA，et al. Spherical capsules in three dimensional unbounded stokes flows:effect of the membrane constitutive law and onset of buckling［J］.Fluid Mech，2004，516:303－334.

［7］Lac E，Barthès-Biesel D.Deformation of a capsule in simple shear flow:effect of membrane prestress ［J］.Phys Fluids，2005，17:72－105.

［8］Peskin CS.The immersed boundary method［J］.Acta Numer，2002，11:479－517.

［9］Eggleton CD，Popel AS.Large deformation of red blood cell ghosts in simple shear flow［J］.Phys Fluids，1998，10:1834 －1845.

［10］Keller SR，Skalak R.Motion of a tank-treading ellipsoid particle in a shear flow［J］.Fluid Mech，1982，120:27－47.

［11］Yu Huidan，Luo LS，Girimaji SS.LES of turbulent square jet flow using an MRT lattice Boltzmann model［J］.Comput Fluids，2006，35:957 －965.

［12］Feng ZG，Michaelides EE.Proteus:a direct forcing method in the simulations of particulate flows［J］.Comput Phys，2005，202:20－51.

［13］Peng Yan，Luo LS.A comparative study of immersed-boundary and interpolated bounce-back methods in LBE ［J］.Prog Comput Fluid Dyn，2008，8:156－167.

［14］Filippova O，Hanel D.Grid refinement for lattice-BGK models［J］.Comput Phys，1998，147:219 －228.

［15］Yu Dazhi，Girimaji SS.Multi-block lattice Boltzmann method:extension to 3D and validation in turbulence［J］.Physica A，2006，362:118－124.

［16］Peng Yan，Shu C，Chew YT，et al.Application of multi-block approach in the immersed boundary-lattice Boltzmann method for viscous fluid flows［J］.Comput Phys，2006，218:460 － 478.

［17］Sui Y，Chew YT，Roy P，Low HT.Inertia effect on the transient deformation of elastic capsules in simple shear flow［J］.Comput Fluids，2009，38:49 －59.

［18］Sui Y，Chew YT，Roy P，et al.A hybrid method to study flowinduced deformation of three-dimensional capsules［J］.Comput Phys，2008，27:6351 －6371.

［19］Tryggvason G，Bunner B，Esmaeeli A，et al.A front-tracking method for the computations of multiphase flow［J］.Comput Phys，2001，169:708 －759.

［20］Unverdi SO，Tryggvason G.A front-tracking method for viscous，incompressible，multi-fluid flows ［J］.Comput Phys，1992，100:25－37.

［21］Lee J，Pozrikidis C.Effect of surfactants on the deformation of drops and bubbles in Navier——Stokes flow ［J］. Comput Fluids，2006，35:43 －60.

［22］Bagchi P，Johnson PC，Popel AS.Computational fluid dynamic simulation of aggregation of deformable cells in a shearflow［J］.Biomech Eng，2005，127:1070－1080.

［23］Li Xiaoyi，Sarkar K.Front-tracking simulation of deformation and buckling instability of a liquid capsule enclosed by an elastic membrane［J］.Comput Phys，2008，227:4998 －5018.

［24］Lallemand P，Luo LS，Peng Yan.A lattice Boltzmann fronttrack method for interface dynamics with surface tension in twodimensions［J］.Comput Phys，2007，226:1367 －1384.

［25］Shrivastava S，Tang J.Large deformation finite element analysis of non-linear viscoelastic membranes with reference to thermoforming［J］.Strain Anal，1993，28:31 －51.

［26］Minale M.A phenomenological model for wall effects on the deformation of an ellipsoidal drop in viscous flow［J］.Rheol Acta，2008，47:667－675.

［27］Lee J，Pozrikidis C.Effect of surfactants on the deformation of drops and bubbles in Navier-Stokes flow ［J］.Comput Fluids，2006，35:43－60.