高应力下砂土与结构界面单剪试验研究
2011-06-08郭佳奇刘希亮苏承东
郭佳奇,刘希亮,苏承东
(河南理工大学a.土木学院;b.能源科学与工程学院,河南焦作454000)
土与结构界面力学特性的研究是解决土与结构相互作用问题(SSI)的关键。20世纪60年代以来,有关学者就开展了土与结构界面相互作用力学性质的研究,取得了大量的理论成果[1-4]。土与结构界面相互作用往往具有剪切面积固定、界面土体自由变形等特征,上述基于传统及改进的直剪仪取得的成果无法或者只能部分考虑满足界面剪切力学特征,因此很多学者开始利用单剪仪开展界面相互作用问题的研究:Uesugi等[5-6]用单剪仪对砂与钢板界面的力学性能进行了较为深入的研究;M ohajeri等[7]利用由传统的直剪装置改装的单剪仪,进行了一系列旨在研究地震诱使的非饱和、相对密实的砂性土的变形、应力-应变关系以及循环剪切变形的试验;卢廷浩等[8]进行了较为详尽的土与不同结构界面的剪切试验,观察了界面的错动位移和剪切位移。高俊合等[9]进行了土与混凝土界面的大型单剪试验,据试验结果分析界面剪切破坏带,并得到其厚度;徐泽友等[10]通过高塑性黏土与混凝土接触面大型单剪试验研究了高塑性黏土与结构接触面的剪切应力-剪切应变关系及强度参数;王伟[11]进行了17%、20%、24%共3组含水率的土与混凝土接触面正反向单剪试验,研究了正反向剪切时接触面强度参数之间的关系。
单剪条件下土与结构界面的力学状态更接近真实情况,已取得的试验成果有力地推动了此领域的研究,但上述研究均是在低应力或极低应力条件下开展的,随着深部地下工程的大量出现,使得原来针对浅部土体进行的低应力条件下界面相互作用的试验成果的应用受到了挑战,迫切需要开展高应力条件下土与结构界面相互作用问题的研究。从公开发表的文献来看,目前高应力条件下土与结构界面相互作用方面的研究成果还较少[12-14],且多为在直剪条件下获得的。笔者在RM T-150B试验系统的平台上自行改装、加工了高应力单剪试验系统,其垂直荷载能达到1 000 kN、剪切荷载达到500 kN。在此试验系统上对饱和砾砂(L)、粗砂(C)、中砂(Z)、细砂(X)同钢材(G)/混凝土(H)的界面剪切力学特性进行了研究。
1 高应力单剪试验
1.1 试验系统
目前生产的直剪仪或单剪仪法向荷载均较小,无法满足试验所要求的法向应力水平。笔者在岩石力学试验系统(RM T-150B)的平台上进行了加工、改装,重点对单剪盒以及加载帽、减阻板等配套装置进行了专门设计加工,以满足试验要求,改装后的试验系统见图1。高应力单剪仪试验系统利用RMT-150B独具特色的拉剪方式,垂直方向与水平方向的液压缸均为伺服控制,加载帽与垂直推杆、水平拉杆端头与支撑、下剪切盒与基座间均设置滚轴,以提高试验精度。

图1 高应力单剪仪示意图
上剪切盒由20个叠放在一起的钢环组成,每个圆环的内部尺寸为 d×h=150 mm×3 mm。将RM T-150B试验系统上的剪切盒卸掉,直接用基底代替。混凝土基底由C30混凝土在特制的木模型盒中浇筑成型,见图2;钢材基底由硬度为36.0HRC的45号钢加工而成,表面进行拉毛处理,见图3。
图2 混凝土基底

图3 钢材基底
在剪切过程中,砂土试样放置在由叠环组成的上剪切盒中,垂直方向油缸的荷载通过上垫板、滚轴板、下垫板及加载帽传递到试样上,在整个剪切过程中法向荷载保持恒定。叠环本身不承受法向荷载作用,且内部加工非常光滑,因此可以忽略叠环和基底(下剪切盒)之间的摩擦力,认为界面剪切力完全来自界面相互作用。
1.2 试样准备及试验方法
试样按如下步骤进行制备:1)取适量建筑砂(筛除碎石)在室外自然风干;2)在室内烘箱内106℃下,烘2 h然后取出;3)筛分出 0.075 mm 以下、0.075~ 0.25 mm 、0.25~ 0.5 mm、0.5 ~ 2 mm、2 mm以上5个粒径组;4)按文献[15]要求配制砾砂、粗砂、中砂、细砂,各砂土特征粒径见表1;5)按文献[15]要求,用饱和器对试样进行饱和,将饱和后的试样放入塑料袋中,扎紧袋口放置于保湿桶内,并测定试样的饱和密度,各砂土的饱和密度见表1。
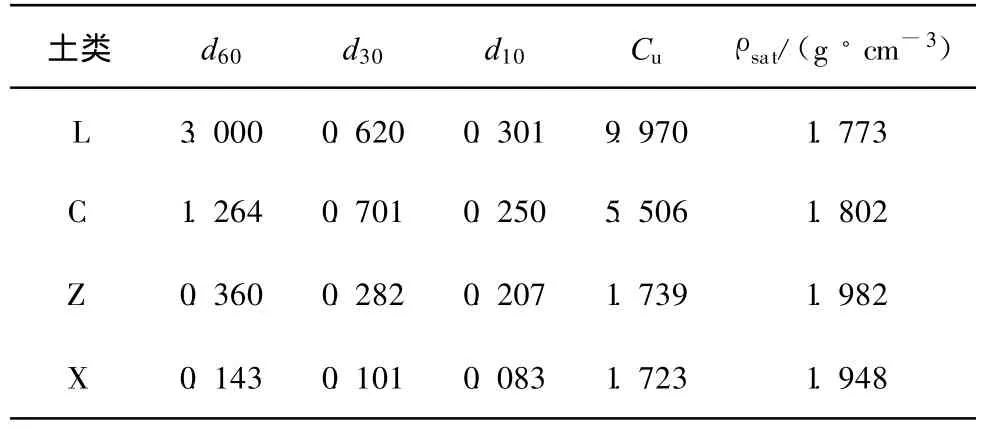
表1 砂土特性参数
在剪切试验中,首先按上剪切盒容积计算所需试样的质量,并放置于剪切盒中,在一定法向荷载(法向荷载加载速率为5 kN/s)下对试样进行固结,固结稳定标准基本上控制在0.002 5 mm/m in;然后,在法向荷载恒定的条件下,进行界面剪切试验,剪切速率设定为0.2 mm/min,在剪切过程中记录界面的剪应力、相对剪切位移及试样的法向位移,当界面剪切应力基本保持不变或界面相对剪切位移接近20 mm时停止试验。
1.3 试验方案
试验中采用粗糙混凝土和表面拉毛钢材2种基底模拟结构物;配制饱和砾砂、饱和粗砂、饱和中砂、饱和细砂4种土样;当地下工程埋深超过100m时,在土层中水平地压可采用p=K◦H(K为计算系数,中国取0.01~0.03)进行计算[16],目前深部地下工程的埋深大多为50~500 m,按上式试算水平地压为1~10M Pa(计算中K取0.02)。试验中法向应力取4、6、8、10MPa 4个应力水平。按基底、土性及法向应力水平的组合情况进行试验,共进行了32(◦◦)组试验。
2 试验结果
根据在试验过程中采集的相关数据,绘制界面剪应力-相对剪切位移关系曲线,见图4。
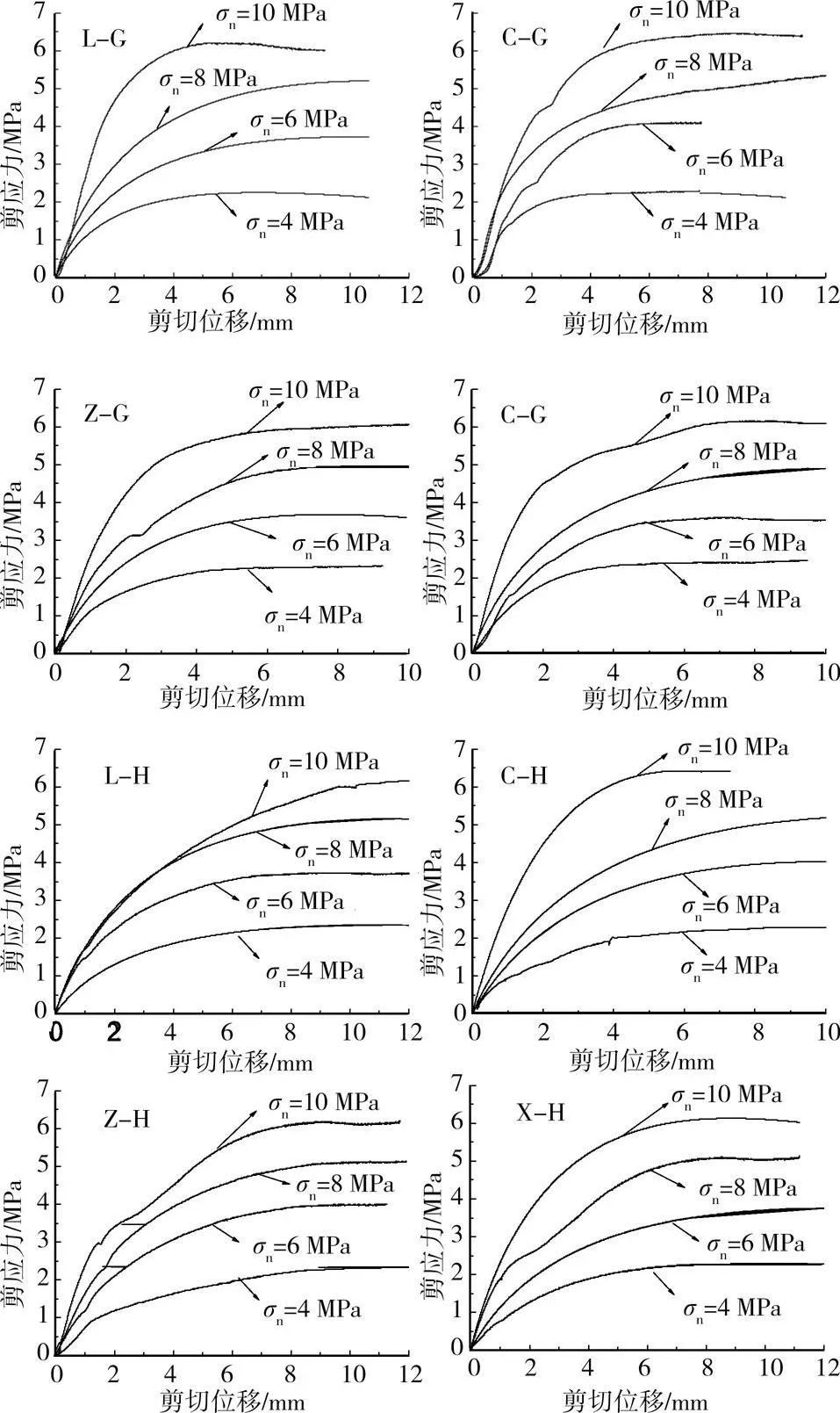
图4 剪应力-剪切位移关系
由图4知,不同界面间的剪应力-剪切位移曲线在高应力水平下几乎具有相同的变化趋势。高应力单剪条件下二者关系曲线在达到最大剪应力之前,呈非线性弹性关系,达到最大剪应力以后,呈理想塑性关系,整个过程可以用非线性弹性-理想塑性来描述;而在高应力直剪条件下,在整个剪切过程中二者关系具有非线性弹性特征[12-13]。
3 试验结果分析
界面本构模型的确定是土与结构相互作用问题的研究重点,从图4知高应力单剪条件下界面剪切变形特性类似于栾茂田、武亚军等人[17]提出的NEPP模型,因此有必要对NEPP模型在高应力单剪条件下的适用性进行讨论。
3.1 NEPP模型的不足
根据图4中试验曲线特性及相关文献的研究成果[18]知,界面剪应力-相对剪切位移关系拟合曲线必须具有以下性质:
1)经过(0,0)点;
2)曲线处处一阶可导,初始一阶导数可变;
3)单调递增,有上界,且曲线外凸。
NEPP模型屈服前剪切变形特性采用双曲线非线性弹性模型描述;屈服后,采用完全塑性理论描述,此时界面剪应力恒定不变、相对剪切位移持续增加,二者关系为一条平直线。假定剪应力-相对剪切位移曲线由双曲线过渡到平直线时(即界面剪应力达到最大值时)剪切位移为w s0,剪应力-相对剪切位移曲线在点()处的左导数为:

右导数为:

进一步的研究表明曲线段试验数据在ws/τ-ws坐标系中是一条下凹的光滑曲线,并不是由NEPP模型所分析的直线[19]。
3.2 威布尔分布曲线
威布尔分布曲线具有较大的灵活性和适应性,该文采用一种应用较为普遍的三参数威布尔分布曲线来描述界面的剪应力-相对剪切位移关系,关系式如下:

式中:a为界面初始剪切刚度;b为与剪切位移有关的回归参数;c为曲线形状参数,其物理意义是局部强度变化的测度,称为均匀性指标。当a、b一定时,威布尔分布曲线形状随c值变化而变化,见图5。

图5 不同c值的威布尔分布曲线(a=3、b=1)
从图5中可知,三参数威布尔分布曲线在不同的形状参数下能拟合应变硬化、应变软化以及理想塑性流动状态。文献[18]研究认为,较为理想的界面本构模型应保证初始剪切刚度、极限抗剪强度和半值收敛指数独立或者相对独立,在初始剪切刚度和极抗剪限强度一定的情况下仍能反映剪应力-相对剪切位移关系曲线的收敛速度。半值收敛指数定义为:对于单调递增且有极限值的函数,当函数值达到极限的一半时,自变量的数值称为曲线的半值收敛指数。
如图5所示,当参数适当时,三参数威布尔分布曲线可以描述从非线性弹性阶段到塑性流动阶段的全过程,此时三参数威布尔分布曲线是单调递增且有极限值的,满足半值收敛指数定义的前提条件。当导数为零时,曲线取得极限值为:

当函数值达到τu/2时,此时相对剪切位移即半值收敛指数为:
初始剪切刚度为:

因此,可以描述理想塑性流动的三参数威布尔分布曲线的数学特征方程为:
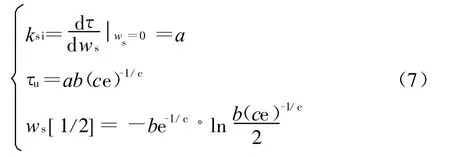
3个特征方程有3个相互独立的未知参数。在初始剪切刚度和极限剪应力值确定的情况下,只要b、c取值满足极限抗剪强度值确定,b、c仍可以相对自由取值,即半值收敛指数相对独立于初始剪切刚度和极限抗剪强度,界面剪应力—相对剪切位移曲线收敛速度可变,即采用三参数威布尔分布曲线拟合试验数据时线型可调,拟合精度更高。
3.3 2种模型的比较
用三参数威布尔分布曲线代替NEPP模型中的双曲线形成新的非线性弹性-理想塑性界面模型(WNEPP),屈服前界面上的非线性剪切变形特性采用三参数威布尔分布曲线描述,而塑性屈服后,在恒定屈服应力作用下界面剪切带内所产生的滑移错动变形则采用完全塑性理论描述。随机选取4组试验数据分别采用NEPP模型和WNEPP模型进行拟合,拟合结果对比见图6。

图6 两种模型拟合曲线比较
由图6知,WNEPP模型的拟合曲线相对于NEPP模型的拟合曲线拟合精度更高,更接近试验曲线,且光滑连续,而NEPP模型的拟合曲线不但精度差且存在奇异点(图中NEPP模型拟合曲线的奇异点为(w s0,τu),该点存在原因见3.1节分析)。
4 高应力下界面的剪切刚度
4.1 试验数据的回归
将试验数据按WNEPP模型进行回归,结果见表2。
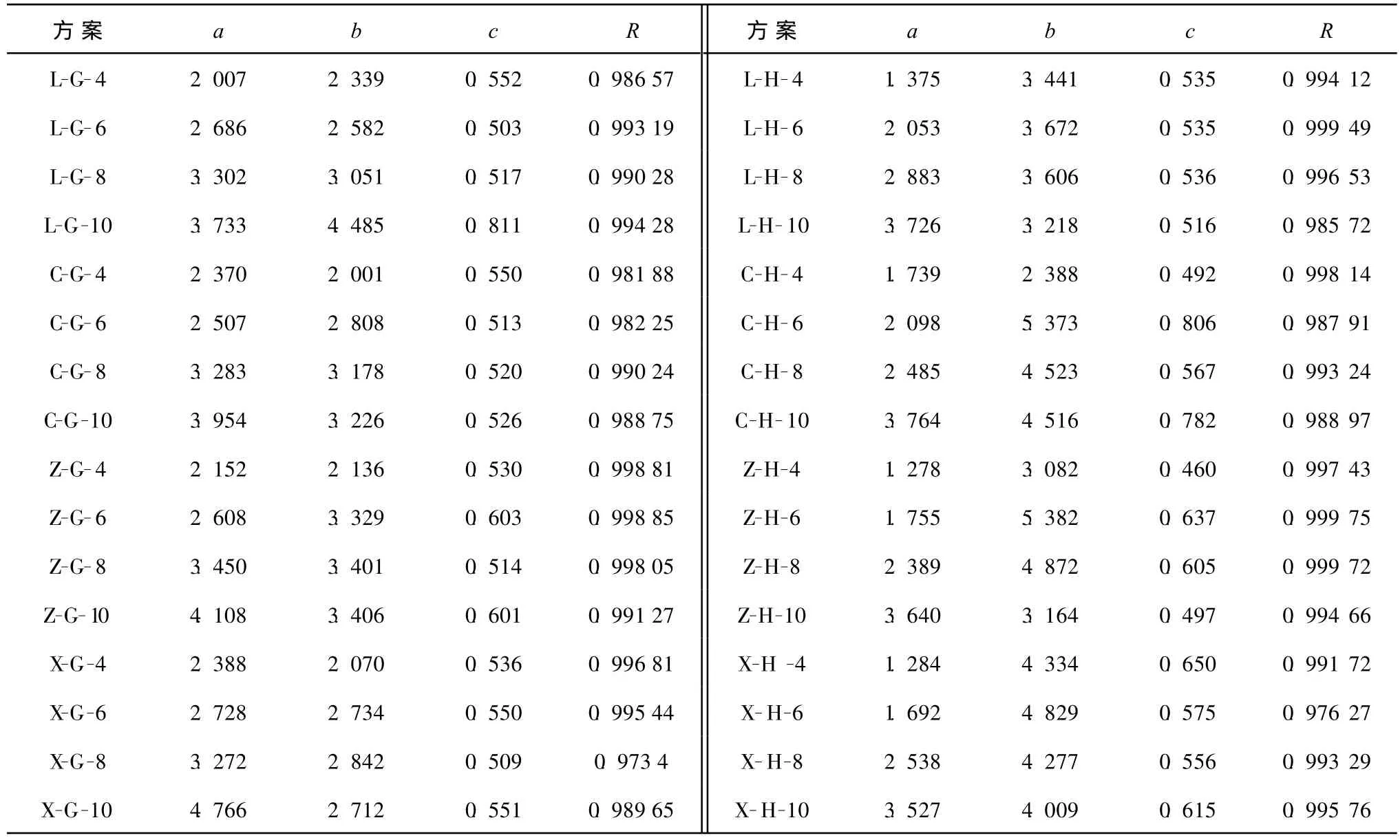
表2 试验数据按WNEPP模型回归结果
4.2 初始剪切刚度
界面剪切刚度定义为界面产生单位相对剪切位移时所需要的剪应力。它不仅与界面的材料性质有关,而且与法向应力水平密切相关。
由式(6)知表2中相应条件下的回归参数a即为该条件下界面初始剪切刚度。文献[2、8]均认为低应力条件下界面初始剪切刚度与法向应力呈幂函数关系,该文参考上述文献的研究成果将同种界面的初始剪切刚度同法向应力进行回归分析,回归方程为幂函数(ksi=Kσn)和线性函数(ksi=A+Bσ)。回归结果见表3。从回归结果看,高应力单剪条件下,界面初始剪切刚度与法向应力的关系用线性函数描述较好。
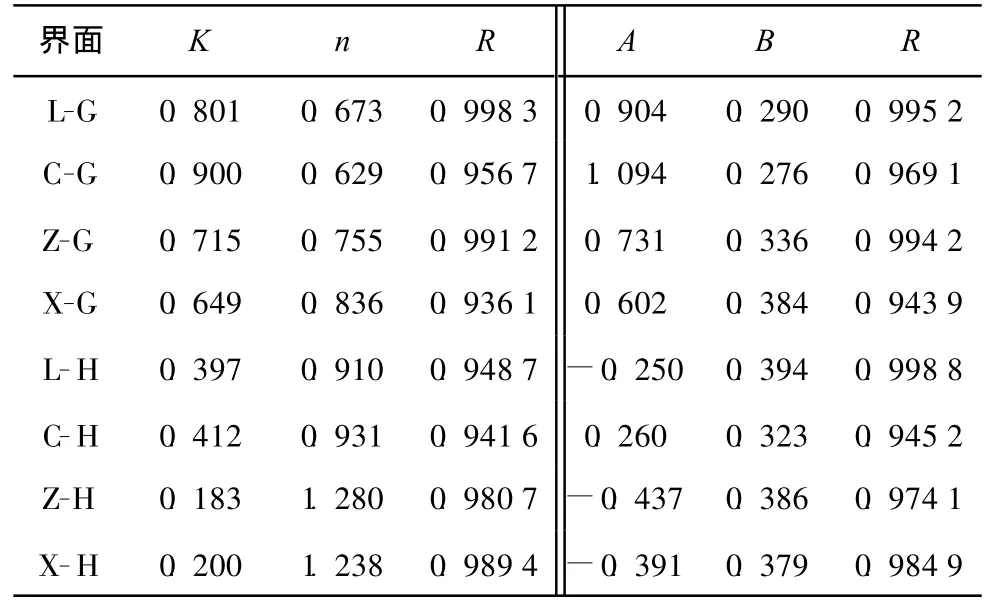
表3 界面初始剪切刚度回归结果 /(MPa◦mm-1)
4.3 界面剪切刚度
界面剪应力-相对剪切位移关系曲线的斜率定义为界面剪切刚度kst[20]。根据WNEPP模型的特征,高应力单剪条件下界面剪切刚度屈服后为零,屈服前由公式(3)可定义为:
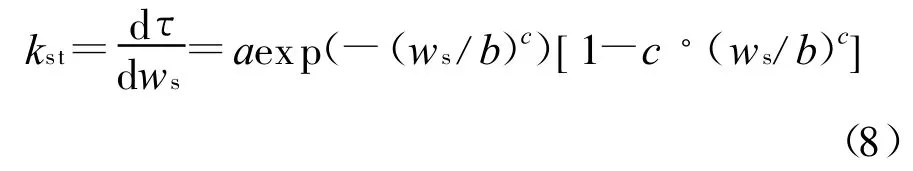
将表2的回归参数带入上式可得相应条件下界面刚度和剪切位移关系式。根据4.2节的分析结果式(8)可改写为:
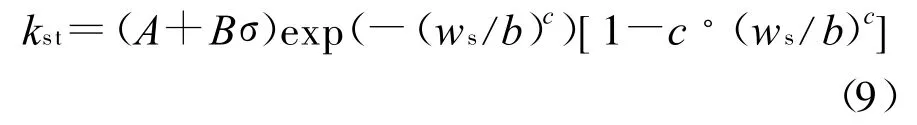
由上式知,剪切刚度是法向应力和剪切位移的函数。
为验证式(8)的精度,抽取2组试验数据绘制特定法向应力下界面剪切刚度随剪切位移的变化趋势,见图7。图中界面剪切刚度试验值由O rigin软件中的Tangent插件处理图3中相应试验曲线后得到;图中NEPP模型的剪切刚度与剪切位移关系按如下过程确定,按NEPP模型屈服前剪应力与剪切位移关系式(τ=w s/(aw s+b))回归相应试验数据,获得参数a、b,将上述参数代入文献[21]中的式(3)得NEPP模型屈服前界面剪切刚度与剪切位移关系式,屈服后剪切刚度为零。
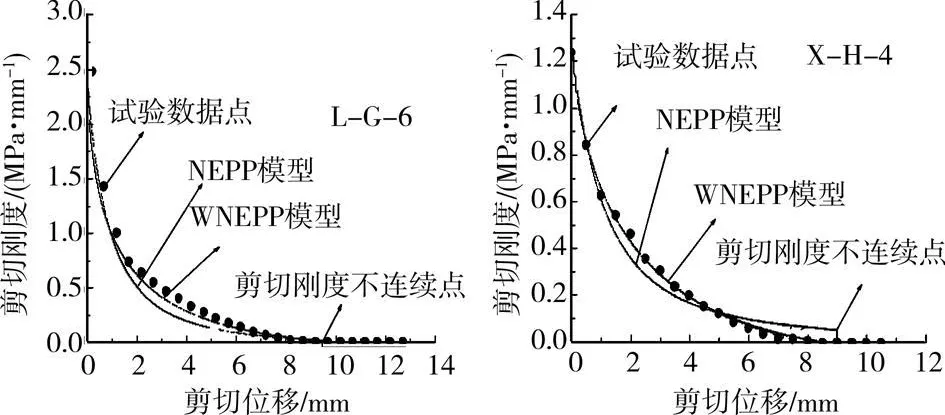
图7 界面剪切刚度变化趋势
5 结论
通过在自行改装、加工的高应力单剪仪上进行了一系列饱和砾砂、粗砂、中砂、细砂同钢材及混凝土界面的剪切试验,得到如下结论:
1)高应力单剪条件下界面平均剪应力同相对剪切位移关系不同于直剪试验的结果,呈非线性弹性-理想塑性特征。
2)NEPP模型的拟合曲线存在非光滑连续的不足,同时由于双曲线模型本身的不足致使NEPP模型不适合描述高应力单剪条件下界面剪切变形特征。通过数学方法证明三参数威布尔分布能克服上述不足,用威布尔分布曲线取代NEPP模型中的双曲线形成新的界面模型,能更好的拟合试验数据。
3)高应力下界面初始剪切刚度的回归分析表明线性函数更适合描述初始剪切刚度同法向应力的关系。界面剪切刚度随相对剪切位移(界面的破坏程度)增加而减小,是法向应力和相对剪切位移的函数。基于新模型建立的界面剪切刚度变化趋势与剪切刚度试验值较接近,较基于NEPP模型建立的剪切刚度变化趋势精确。
[1]POTYONDY JG,ENG M.Skin friction between various soils and construction materials[J].Geotechnique,1961(11):339-353.
[2]CLOUGH GW,DUNCAN JM.Finiteelementanalysis of retaining w all behavior[J].Journal of the Soil Mechnanics and Foundations Division,1971,97(SM 12):1657-1674.
[3]PETERSON M S,KULHAWY F H,NUCCIL R,et al.Stress-deformation behavior of soil-concrete interface[R].Contract Report B-49 to Niagara Mohawk Power Corporation.Sy racuse,NY,1976.
[4]ZAM AN M M,DESA I C S,DRUMN E C.Interface model for dynam ic soil-structure interaction[J].ASCE Journal of Geotechnical Engineering,1984,110(9),1257-1273.
[5]UESUCIM,KISH IDA H,TSUBAKIHARA Y.Behavior of sand particles in sand-steel interface[J].Soils and Foundations,1988,28(1):107-118.
[6]K ISHIDA H,UESUCI M.Test of interface between sand and steel in the simp le shear apparatus[J].Journal of Geotechnique,1987,37(1):45-52.
[7]MOHAJERI M,TOWHATA I.Stress-strain behavior of compacted sandy material under cyclic simple shear[J].Soils and Foundations,2003,43(6):75-89.
[8]张冬霁,卢廷浩.一种土与结构接触面模型的建立及其应用[J].岩土工程学报,1998,20(6):62-66.ZHANG DONG-JI,LU TING-H AO.Estab lishment and application of a interface model between soil structure[J].Chinese Journal of Geotechnical Engineering,1998,20(6):62-66.
[9]高俊合,于海学,赵维炳.土与混凝土接触面特性的大型单剪试验研究及数值模拟[J].土木工程学报,2000,33(4):42-46.GAO JUN-HE,YU HA I-XUE,ZHAO WEI-BING.Characteristics study o f interface between soils and concrete by using large size single shear apparatus and numerical analysis[J].China Civil Engineering Journal,2000,33(4):42-46.
[10]徐泽友,卢廷浩,丁明武.高塑性黏土与混凝土接触面剪切特性[J].河海大学学报:自然科学版,2009,37(1):71-74.XU ZE-YOU,LU TING-HAO,DING M ING-WU.Shear properties at interface between highly p lastic clay and concrete[J].Journal of H ohai University:Natural Sciences,2009,37(1):71-74.
[11]王伟,卢廷浩,宰金珉,等.土与混凝土接触面反向剪切单剪试验[J].岩土力学,2009,30(5):1303-1306.WANG WEI,LU TING-HAO,ZAI JIN-M IN,et al.Negative shear test on soil-concrete interface using simp le shear apparatus[J].Rock and Soil Mechanics,2009,30(5):1303-1306.
[12]刘希亮,朱维申,李术才.高应力作用界面剪切性质的试验研究[J].岩石力学与工程学报,2004,23(3):408-414.LIU XI-LIANG,ZHU WEI-SHEN,LI SHU-CAI.Testing study on interface shear p roperties under high pressure[J].Chinese Journal of Rock Mechanics Engineering,2004,23(3):408-414.
[13]ZHOU GUO-QING,XIA HONG-CHUN,ZHAO GUANG-SI,et al.Non linear elastic constitutive model o f soil-structure interfaces under relatively high normal stress[J].Journal o f China University o f M ining&Technology,2007,17(3),301-305.
[14]周国庆,夏红春,赵光思.深部土—结构接触面与界面层力学特性的直接剪切试验[J].煤炭学报,2008,33(10):157-1162.ZHOU GUO-QING,XIA HONG-CHUN,ZHAO GUANGSI.Direct shear experiment of deep soil.structure interface and interface layer mechanical characteristics[J].Journal of China Coal Society,2008,33(10):157-1162.
[15]GB/T 50123-1999土工试验方法标准[S].北京:中国计划出版社,1999.
[16]刘希亮.深厚表土不稳定地层中井壁受力研究[M].北京:煤炭工业出版社,2004.
[17]武亚军,栾茂田,杨敏.土与结构间一种新的接触单元模型[J].同济大学学报:自然科学版,2005,33(4),432-435.WU YA-JUN,LUAN M AO-TIAN,YANG M IN.New contact element o f interface betw een soil and structure[J].Journal of Tongji University:Natural Science,2005,33(4),432-435.
[18]王伟.基于能量耗散原理的土与结构接触面模型研究及应用[D].南京:河海大学,2006.
[19]郭佳奇.高应力下土与结构界面单剪试验及本构关系研究[D].焦作:河南理工大学,2007.
[20]朱百里,沈珠江.计算土力学[M].上海:上海科技出版社,1990.
[21]郭佳奇,刘希亮,乔春生,等.高应力下干砂与饱和砂单剪特性比较[J].北京交通大学学报:自然科学版,2010,34(1),68-72.GUO JIA-QI,LIU XI-LIANG,QIAO CHUN-SHENG,et al.Comparison of the simple shear p roperty between d ry and saturated sand under high stress[J].Journal of Beijing Jiaotng University:Natural Science,2010,34(1),68-72.
