水流对浮体作用的SPH方法模拟
2011-06-07蒋昌波程永舟
肖 潇 , 蒋昌波 , 程永舟
(1长沙理工大学 水利工程学院,长沙410004;2湖南省水沙科学与水灾害防治重点实验室,长沙 410004)
水流对浮体作用的SPH方法模拟
肖 潇1,2, 蒋昌波1,2, 程永舟1,2
(1长沙理工大学 水利工程学院,长沙410004;2湖南省水沙科学与水灾害防治重点实验室,长沙 410004)
水流与浮体相互作用时,运动情况十分复杂,目前很难准确有效地模拟。而SPH作为一种纯拉格朗日方法,无需构建网格,用核函数近似粒子进行离散,能较好地解决一些自由面大变形问题。文章利用SPH法对溃坝时引起的高速水流冲击浮体以及水体晃动时破损浮体的运动过程进行模拟。模拟结果表明,SPH法能有效地进行水流对浮体作用的研究。
浮体;光滑粒子流体动力学;移动最小二乘法;核函数;数值模拟
1 引 言
光滑粒子流体动力学(Smoothed Particle Hydrodynamics)法[1]是模拟流体流动的一种无网格拉格朗日粒子法,最初被用于解三维开放空间天体物理学问题。基本思想是将连续系统用一系列粒子来描述,这些粒子携带独立的物理信息并遵循物理控制方程进行运动。这种方法无需网格及质点间相互作用的计算,使得大变形问题的处理变得容易。
近年来SPH法不断发展、改进和完善,逐渐趋向于成熟,并应用于很多领域。Sigalotti等[2]运用SPH法模拟了强冲击过程,Bulian等[3]运用SPH法模拟了不同角度情况下箱中水体的晃动。Marongiu等[4]结合SPH-ALE法模拟了水轮机的自由表面流动,Capone等[5]运用SPH法进行了滑坡涌浪的模拟,以及Narayanaswamy[6]将SPH与Funwave结合进行了近岸波浪传播过程的模拟等。在国内也有一些学者进行了SPH法的研究应用,宗智等[7]进行了二维水下爆炸问题的SPH数值模拟,崔岩等[8]进行了二维矩形水槽晃荡过程的SPH数值模拟,李大鸣等[9]进行了大坝表孔泄流的SPH数值模拟,但作为一个日趋成熟和完善的方法,SPH法的优势还未被完全发挥。
在海洋、河流中高速水流对船舶等水上漂浮物的运动影响很大,使得它们的运动轨迹发生很大变化,因此,需要研究其运动规律,降低水流冲击的破坏程度。对这类问题有不少学者进行了相关研究。Contento等[10]简单地计算了波浪对不规则浮体的作用,Hadži等[11]用网格法进行了波浪作用下浮体运动情况的模拟,Yan等[12]用QALE-FEM方法进行了非线性波与浮体相互作用的模拟,王大国等[13]进行了波浪对箱形船作用的计算,王化明等[14]进行了船舶在浅水域横向停靠运动粘性水动力计算。这些研究都为解决实际问题提供了良好的依据。基于欧拉网格的方法,由于网格的局限性,对高速水流作用下浮体的大幅度运动情况下不能很好地进行模拟,而SPH法却能很好地解决这个问题。
本文利用SPH方法,对溃坝引起的高速水流对浮体的冲击作用,以及水体晃动对开口浮体影响进行了二维数值模拟,以此分析高速水流冲击作用下浮体的运动过程。
2 计算模型
2.1 SPH基本原理
在SPH方法中,任一宏观变量都能借助于一组无序点上的值表示成积分插值计算得到。对于任意函数A()r[1]有:


将(1)式转化为支持域内所用粒子叠加求和的离散化形式,则在粒子a处的函数可表示为:

式中:mb为粒子质量;ρb为粒子密度,Wab=ra-rb′,( )h为核函数。
SPH方法中所用的核函数应具有归一性、紧支性、非负性、衰减性、δ函数性质、对称性质和光滑性等特性[9,15]。目前,使用较多的核函数有Gaussian函数、B样条函数、高次核样条函数等,本次数值模拟采用目前应用比较广泛的三次样条核函数:

式中:αD应用于二维问题时取;q为相对长度,q=。
2.2 基本方程
SPH方法引入基本方程进行离散,采用人工粘性来产生剪切粘性[16]和体积粘性,得到离散形式的基本方程组为:


浮体的运动情况控制采用以下方程:

式中:fk是边界粒子k单位质量所受的作用力;fka是水粒子a对边界粒子k的单位质量作用力;WPs是对边界粒子k有影响的水粒子;mk是粒子k的质量;ma是粒子a的质量;M是浮体的质量;V是浮体的速度;BPs是浮体的边界粒子;I是惯性力;Ω是浮体的旋转速度;R0是重心的位置;uk是边界粒子k的速度。
粒子密度采用移动最小二乘法修正[17]后的密度求和公式进行求解,该方法能有效地克服边缘效应。边界条件采用Dalrymple(2000)[18]提出的动力边界条件,该方法使边界粒子满足流体粒子一样的方程,但是它们需满足固壁不可滑移的条件。
3 模型验证
图1为溃坝实物模型示意图,水箱长、宽、高为4m×0.1m×3m,水体长、宽、高为1m×0.1m×2m,水体前放置一挡板[19]。数模计算参照实体模型的剖面进行相应的二维模拟设置,取粒子的初始速度为0,粒间距为0.012m,水体粒子的总数为27 472个,进行溃坝模拟。
图2为典型时刻溃坝过程中水粒子速度分布图,形象地给出了流体和气体界面及流速随时间的演进过程。在t>0时刻,挡板瞬间移开,水体的势能释放为动能,将快速向右下方流动,水体右下方底边界附近速度较大;右上角由于水体的下落,速度也逐渐增大。水体运动过程中,波前峰快速覆盖底部干边界,接近0.8s时,波前峰抵达右侧边壁,此时动能没有完全耗散,水体在惯性作用下沿右侧边壁继续向上运动,动能转化为势能。当水流运动接触到上壁边界时,由于壁面摩檫力和重力作用,达到极限运动高度,开始回落。图3为水流前进过程中波峰到达位置与时间的关系图,与实测数据比较[19,20],最大相对误差不超过10%,结果合理,能很好的反映真实流动。
通过对溃坝过程进行数学模型验证表明:利用SPH方法进行数值模拟结果合理可靠,在流体大变形的模拟上、体积守恒上具有相对的优势,自由表面流的模拟结果合理,因而,该方法能够很好地应用于相关问题的研究。
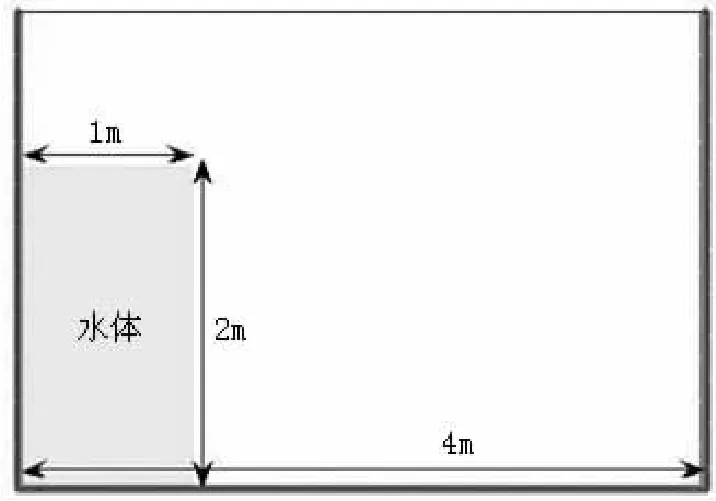
图1 溃坝试验模型示意图Fig.1 Collapses of a water column test model diagram

图2 溃坝过程图Fig.2 Collapses of a water column in a tank
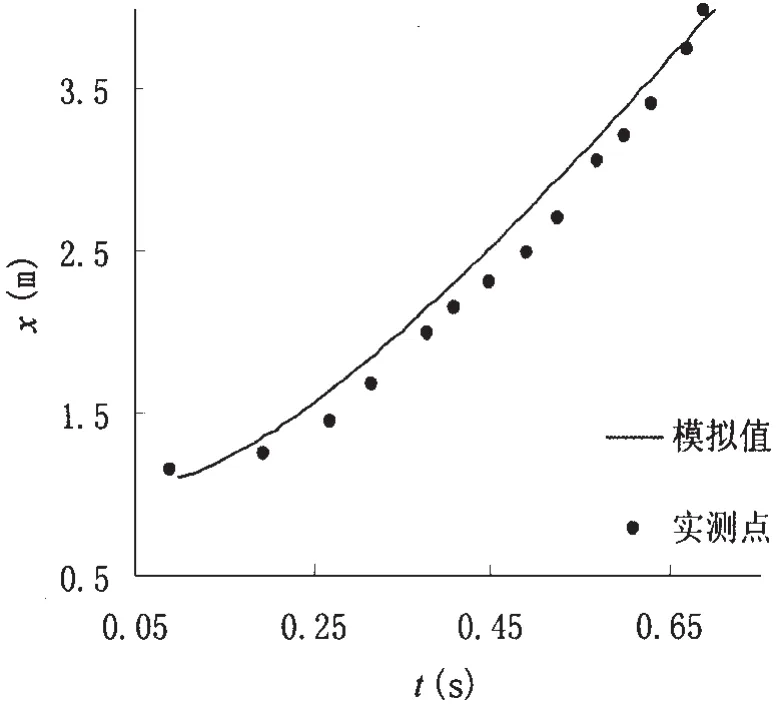
图3 水流到达位置与时间的关系Fig.3 The relation of location flow arriving time
4 水流对浮体作用的数值模拟
4.1 溃坝时高速水流对浮体的冲击作用
图4为假定的溃坝水流对浮体冲击的计算模型平面示意图。浮体边长为0.25m的正方矩形,重1kg,放在水体右下角0.5m高的位置,在槽中2m的位置布置一个高1m的障碍物。数学模型参照实体模型进行相应的二维模拟设置,粒子和其它条件设置都与此前溃坝模型算例相同。
图5给出了溃坝引起的高速水流对浮体的冲击以及障碍物的阻碍作用下整个流动过程随时间变化的分布情况。从图中可以看出挡板被瞬间移开后,水体向右下方塌落并带动浮体向右运动;遇障碍物后,水体在惯性作用下带动浮体向上运动,绕过障碍物,波峰处水体向前方飞溅破碎;在重力作用下,水体和浮体向下回落。
图6给出了浮体在整个冲击过程中所处位置的情况,结合图5可以看出,最初浮体受重力作用下落,后经水流带动移至障碍物前;在惯性作用下随水流上移,达最高位置为1.75m;在重力作用下回落,由水流推动达最右端,即3.25m处,后经墙壁反射回来的水流作用移至2.5m处。
经过对SPH方法模拟溃坝引起的高速水流对浮体的冲击作用的流动过程,该模拟结果接近实际情况,但是具体精确程度需要相关模型试验进一步验证。
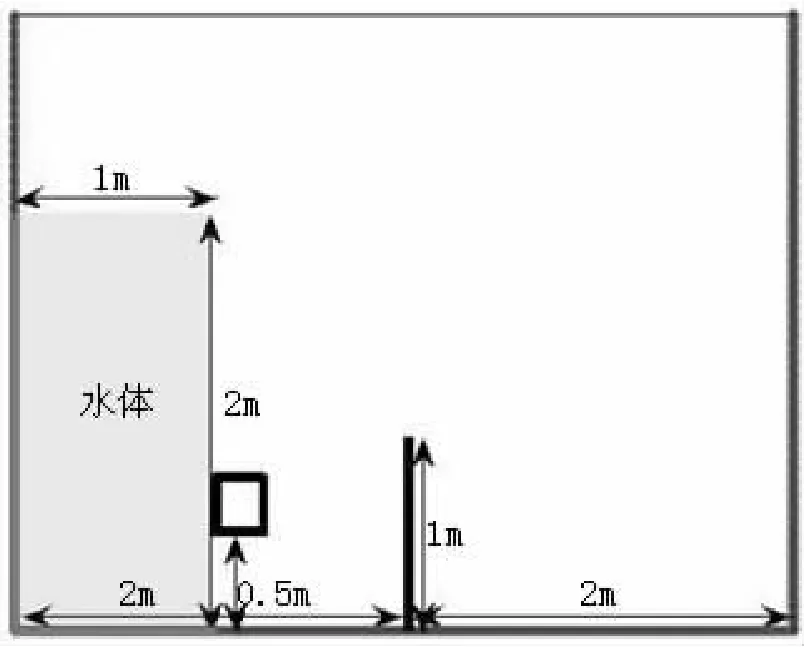
图4 溃坝水流对浮体冲击的模型示意图Fig.4 Flow impact to floating body test model diagram

图5 溃坝水流对浮体冲击的过程Fig.5 Process of flow impact to floating body

图6 浮体整个运动过程的位置情况图Fig.6 Floating body position throughout the movement
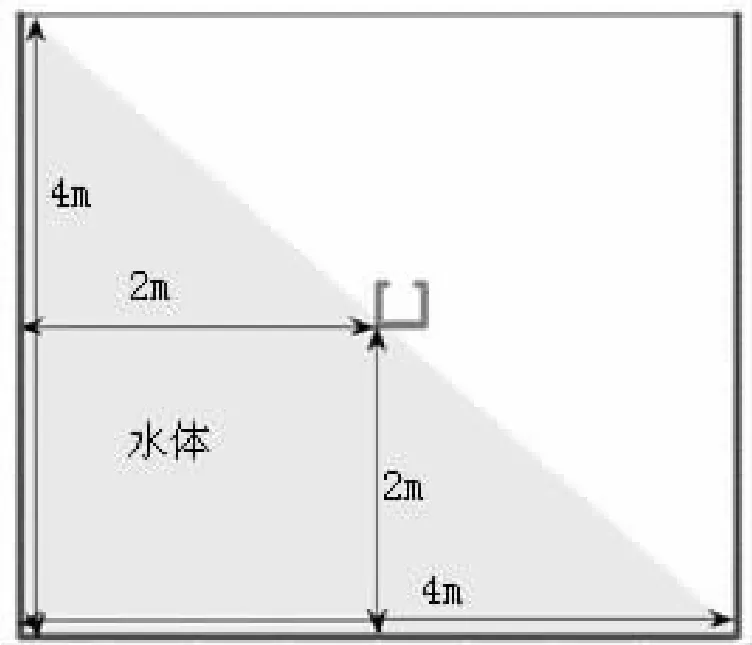
图7 晃动水流对浮体作用的模型示意图Fig.7 Sloshing water on floating body model diagram
4.2 水流晃荡对浮体的作用
图7为假定的水流晃荡对浮体作用的计算模型示意图。浮体边长为0.25m的上方开口的立方体,重0.5kg,水流初始布置为一倾斜的水体。数学模型参照实体模型进行相应的设置,粒子的初始速度都为0,粒间距为0.02m,水体粒子的总数为19 751个。
图8给出了开口浮体在晃动水流作用下整个流动形态过程随时间变化的分布情况。倾斜的水体在重力作用下,向右回落,浮体随液面移动;右侧水体在惯性作用下,沿壁向上运动,水体灌入破损浮体;重力作用下,右侧水体回落,浮体在水流作用下翻转;左侧水体在惯性作用下沿壁向上运动,浮体下沉。由模型计算结果可知,SPH可以模拟在水体晃荡作用下,水流灌入开口浮体的情况。

图8 水体晃动对浮体作用的过程Fig.8 Process of the sloshing water on floating body
5 结 论
本文基于SPH方法,对溃坝引起的高速水流对浮体的冲击作用,以及水体晃动对开口浮体的影响进行了二维数值模拟,分析结果得出以下结论:
(1)利用SPH法对溃坝水流进行数模验证,表明SPH法可用于比较精确地模拟水流的非线性大变形流动问题。
(2)相对于欧拉等网格法,SPH法作为一种拉格朗日法能有效地追踪单个粒子的运动过程,保证整个流体的总体积不变,更能真实地反映实际情况。
(3)SPH方法能很好地追踪浮体的运动轨迹,准确模拟高速水流冲击作用下浮体大幅度运动的过程。
(4)SPH方法能进行水流灌入开口浮体的模拟,很好地反映浮体在波浪作用下的翻转过程。
(5)SPH方法是值得研究发展的方法,今后可以做进一步改进,并进行相关的实物模拟,以获得更广阔的研究空间。
[1]Monaghan J J.Simoothed particle hydrodynamics[J].Annual Rev.Astron.Appl.,1992,30:543-574.
[2]Sigalotti L Di G,Lopez H,Trujillo L.An adaptive SPH method or strong shocks[J].Journal of Computational Physics,2009,228:5888-5907.
[3]Bulian G,Souto-Iglesias A,Delorme L.Smoothed particle hydrodynamics simulation of a tuned liquid damper with angular motion[J].Journal of Hydraulic Research,Extra Issue,2010,48:28-39.
[4]Marongiu J C,Leboeuf F.Free surface flows simulations in Pelton turbines using an hybrid SPH-ALE method[J].Journal of Hydraulic Research,Extra Issue,2010,48:40-49.
[5]Capone T,Panizzo A.SPH modelling of water waves generated by submarine landslides[J].Journal of Hydraulic Research,Extra Issue,2010,48:80-84.
[6]Narayanaswamy M.SPHysics-FUNwave hybrid model for coastal wave propagation[J].Journal of Hydraulic Research,Extra Issue,2010,48:85-93.
[7]宗 智,邹 丽,刘谋斌等.模拟二维水下爆炸问题的光滑粒子(SPH)方法[J].水动力学研究与进展,2007,22(1):61-67.
[8]崔 岩,吴 卫,龚 凯等.二维矩形水槽晃荡过程的SPH方法模拟[J].水动力学研究与进展A辑,2008,23(06):618-624.
[9]李大鸣,刘江川,徐亚男等.SPH法在大坝表孔泄流数值模拟中的应用[J].水科学进展,2008,16(6):841-845.
[10]Contento G.Numerical wave tank computations of nonlinearmotions of wo-dimensional arbitrarily shapedfree floating bodies[J].Ocean Engineering,2000,27:531-556.
[11]Hadži I,Hennig J,Peri a M.Computation of flow-induced motion of floating bodies[J].Applied Mathematical Modelling,2005,29:1196-1210.
[12]Yan S,Ma Q W.Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method[J].Journal of Computational Physics,2007,211:666-692.
[13]王大国,邹志利,唐春安等.波浪对箱形船作用的三维耦合计算模型[J].船舶力学,2007,11(4):533-544.
[14]王化明,邹早建,田喜民等.船舶在浅水域横向停靠运动粘性水动力计算[J].船舶力学,2010,14(7):723-731.
[15]Jin Hongbin,Ding Xin.On criterions for smoothed particle hydrodynamics kernels in stable field[J].Journal of Computational Physics,2005,202:699-709.
[16]Monaghan J J.Simulating free surface flow with SPH[J].Journal of Computational Physics,1994,110:399-406.
[17]Dilts G A.Moving-Least-Squares-Particle Hydrodynamics-I.Consistency and stability[J].Int.J Numer.Meth.Engng,1999,44(8):1115-1155.
[18]Dalrymple R A,Knio O.SPH modelling of water waves[C]//Proc.Coastal Dynamics.Lund,2000:779-787.
[19]Koshizuka S,Oka Y.Moving-particle semi-implicit method for fragmentation of incompressible fluid[J].Nucl Sci Eng,1996,123:421-434.
[20]Gomez-Gesteira M,Rogers B D.State-of-the-art of classical SPH for free-surface flows[J].Journal of Hydraulic Research,Extra Issue,2010,48:6-27.
Simulation of flow-induced floating-body motion with SPH method
XIAO Xiao,JIANG Chang-bo,CHENG Yong-zhou
(1 School of Hydraulic Engineering,Changsha University of Science&Techology,Changsha 410004,China;2 Hunan Province Key Laboratory of Water,Sendiment Sciences&Flood Hazard Prevention,Changsha 410004,China)
Flow-induced floating body motions,that movement is very complicatied,can not be simulated exactly at present.SPH as a Lagrangian method without component grid,uses kernel fuction approximate to particle discretely.And it can solve some problems with strong deformation of free surface.In this paper,SPH method is applied to simulate the process of the floating body motion which results from the collapse of a water column and the movement of damaged floating body in sloshing water.Simulation results show that the SPH method can effectively study the flow indued motion of floating body.
floating body;smoothed particle hydrodynamics (SPH);moving least squares;kernel function;numerical simulation
TV13 U661.1
A
1007-7294(2011)08-0861-06
2010-09-25 修改日期:2011-02-18
国家自然科学基金项目(50909009,50979008);水文水资源与水利工程科学国家重点实验室开放研究基金项目(2008490911);教育部高校博士点基金项目(20094316110002)
肖 潇(1986-),女,硕士研究生,研究方向为水力学及河流动力学,Email:xxxtina@163.com;蒋昌波(1970-),男,长沙理工大学教授,博士生导师。
