Level Set Method for Simulation of Cavitating Flows
2011-06-07
(School of Vehicle and Transportation Engineering,Beijing Institute of Technology,Beijing 100081,China)
Level Set Method for Simulation of Cavitating Flows
HUANG Biao,WANG Guo-yu,ZHANG Min-di,CHEN Wei-qing
(School of Vehicle and Transportation Engineering,Beijing Institute of Technology,Beijing 100081,China)
In this study,the Level set method is presented and applied to multiphase cavitating flows.Herein,this method is applied to flow solver that fully couples the mass,momentum,and transport equation;in numerical simulation,the Level set method with a compressive discretization scheme in both time and space to minimize the smearing of the free surface at the interface is used for simulation of nature and ventilated cavity.In these computations,three cases,including the steady nature cavitating flow around the axisymmetric body and the Clark-Y hydrofoil,and the ventilated cavitating flow around the disk are conducted,compared with the results obtained by simulation with the widelyused mixture model and experimental data,it is shown that,the Level set method is presented specifically to cavitating flows that decreases the interface diffusion where needed.Such an approach is a valid method that could reduce smearing at the cavity interface and also capture the sharp interface between different phases in an efficient and precise manner.
cavitating flow;mixture model;Level set method
Biography:HUANG Biao(1985-),male,Ph.D.student of Beijing Institute of Technology,E-mail:huangbiao@bit.edu.com.
1 Introduction
Cavitating and capturing the motion of the cavity interface in multi-phase fluid flows are a challenging research field of computational fluid dynamics.The motions of cavity interfaces(nature or ventilated supercavities)are important physical phenomenon in many physically interesting.A number of methods have been developed to resolve and track this interface in Computational Fluid Dynamics(CFD)simulating multifuild flows with sharp interfaces listing advantages and disadvantages each.The Level Set method and VOF model are becoming more and more popular to capture the motion of a free surface.The volume of fluid(VOF)method has been widely applied in tracking free interface since it was proposed by Hirt and Nichols[1],in the VOF method,the volume fraction function C is defined first,and the value of C for each cell corresponds to the fraction of fluid filling each cell.Here,the free interface can then be tracked using the interface reconstruction technique and advection algorithm.Important progress has been made in the VOF method by many researchers,such as the SLIC by Noh and Woodward[2],the FLAIR by Ashgriz and Poo[3],the refined reconstruction by Youngs[4],and the CIC-SAM by Ubbink and Issa[5].In parallel,the proposed Level-set formulation is based on the method for interface-fluid flow by reinitializing the interface using a signed distance from the distance.The advantage of the Level set method is the maintenance of the sharp interface which in the VOF method can only be remained by the complicated reconstruction of the interface[6].Numerical algorithms for the Level set equation have been further developed over the past decade.Sussman et al[7]applied the Level set method to incompressible fluid flows in their research;the Level set method is combined for solving the mass conservation equation and the momentum transport equation.Additionally,Shu Bitan et al[8]used the Level set method into OpenFOAM capturing the free interface in incompressible fluid flows;the terminal velocity of rising air bubble in water and the detachment of a bubble from a wall are successfully simulated.For caviating flows,the species-mass-conservation-based Level set method was valued for natural and ventilated cavitating flows.
In present work,in order to capture the distinct interface between different phases in cavitating flows,we provide the results for the validation study of the Level set method.This method is tested on several selected problems for which there are available experimental data of nature and ventilated cavitating flows.Three different test cases for modeling the steady and transient free surface tension have been considered.Special attention is paid to the advantages of this method compared with the numerical results with the other multiphase model-mixture model.
2 Physical and numerical model
The set of governing equations consists of the conservative form of the Reynolds averaged Navier-Stokes equations,plusing a volume fraction transport equation to account for the cavitation dynamics,and the turbulence closure.
2.1 Mixture model
The Navier-Stokes equations in their conservative form governing a Newtonian fluid without body forces and heat transfers are presented below in the Cartesian coordinates:
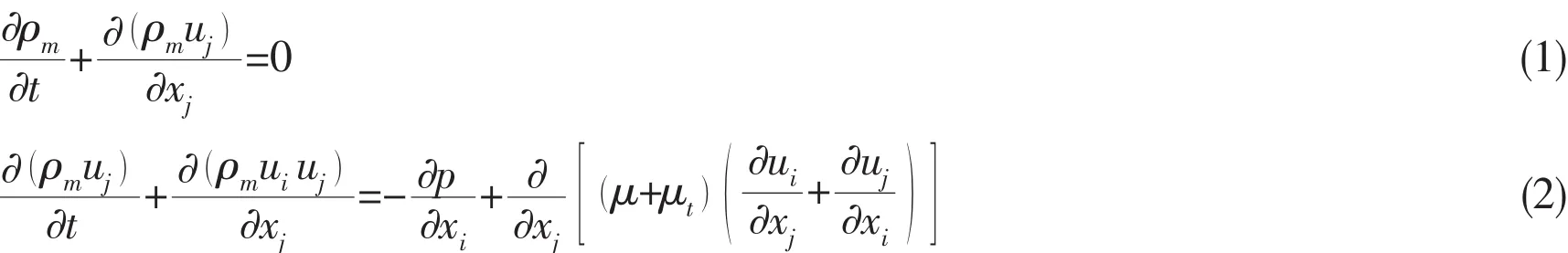
The mixture property,φm,can be expressed as:

where φ can be density,viscosity,and so on.The mixture model is very simple which treats both phases symmetrically.It is appropriate for a calculation of non-disperse liquid-liquid or gas-liquid two phase flow.
2.2 Level set method with mass transfer
The free surface flow model is a homogeneous Eulerian-Eulerian multiphase model,in the Level set method,the interface between the two phases is represented by a continuous scalar function φ( x, t),which is set to zero on the interface,is positive on one side,and negative on the other side.This way both phases are identified,and the location of the physical interface is associated with the surface φ=0.The function φ is called the Level set function and is typically defined as the signed distance to the interface:i.e.,φ=-d( x, t ) on one side of the interface and φ=+d( x, t ) on the other,where d( x, t ) is the shortest distance from the point x to the interface[6].
When the interface is advected by the flow,the evolution of the Level set function is given by:

In the Level set fluid-fluid formulation,the density and viscosity are typically interpolated across the interface as follows:

where subscripts 1 and 2 denote the values corresponding to the two different phases,respectively.Here,Hε(φ ( x ))is a smoothed Heaviside function which is defined in Ref.[7].
When the interface between the fluids is highly curved,then the effect of the surface tension force in the multiphase simulation becomes particularly important.Surface tension acts at the interface between two fluids.Computationally,this is awkward to deal with and the role of surface tension is generally incorporated as a continuum surface force.Using the continuum surface force model,the momentum transport equation for incompressible flow is:

where,the model is based on the continuum surface force model of Brackbill et al[10]which models the surface tension force as a volume force concentrated at the interface.σ is the surface tension coefficient,n is the interface normal vector pointing from the primary fluid to the second fluid(calculated using the volume fraction gradient),and κ is the surface curvature defined by:

For nature cavitating flows,mass transfer is performed within a volume-fraction-based Level set method:

where ρφis the mixture density,ujis the velocity component in Cartesian coordinates,t is the time,+is the condensation rate and˙-is the evaporation rate.In presented study,the source term˙+and˙-denote vapor generation(evaporation)and condensation rates which are depicted in Ref.[11].
In computations,the Level set method uses a compressive discretization scheme in both time and space to minimize the smearing of the free surface at the interface.Typically,this reduces smearing at the interface to two or three layers of cells.The Level-set method is an interface capturing approach rather than an interface reconstruction approach.
2.3 Turbulence model
In present study,the SST model[12]is chosen for steady simulation and the DES model based on the SST formulation is chosen for transient simulation.The advantage of this combination is that the accurate prediction of turbulent boundary layers up to separation and in separated regions carries over from the SST model.In addition,the SST model supports the formulation of a zonal DES formulation[13],which is less sensitive to grid resolution restrictions than the standard DES formulation.
Detached-Eddy Simulation model:
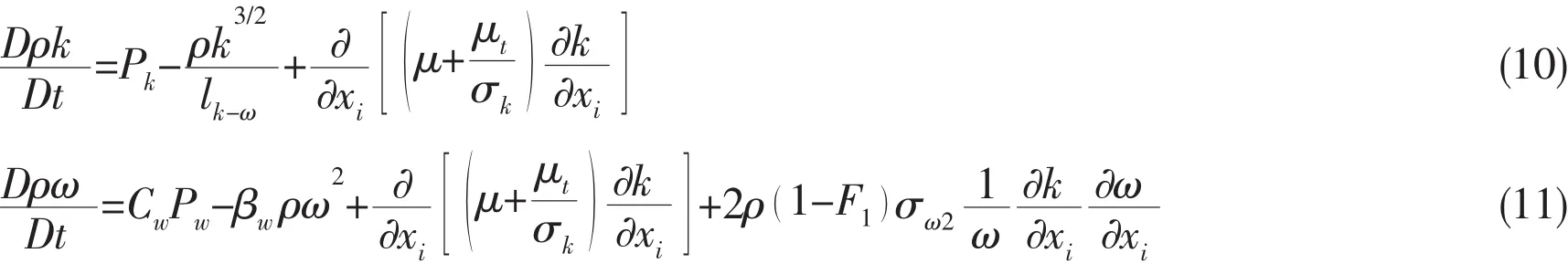
All the coefficients are listed for completeness in Ref.[13],and the eddy-viscosity is defined as:

The length scales of the model in terms of k and ω read:

The idea behind the DES model for Strelets[13]is to switch the SST-RANS model to a LES model in regions where the turbulent length,predicted by the RANS model is larger than the local grid spacing.In this case,the length scale used in the computation of the dissipation rate in the equation for the turbulent kinetic energy is replaced by the local grid spacing.Here,Δ is based on the largest dimension of the grid cell,Δ=max( Δx,Δy,Δz).

For wall-bounced separated flows,the above formulation results in a hybrid model that functions as the standard SST model inside the whole attached boundary layer,and as its sub grid-scale version in the near wake.
3 Results and discussion
3.1 Steady natural cavitation on cylindrical bodies
Rouse and McNown[14]carried out a series of experiments on natural cavitation about ax-isymmetric configurations.For each configuration,measurements were made across a range of cavitation numbers.The hemispherical configuration is computed here,the experiments were performed at Reynolds number greater than 100 000 based on the diameter.As shown in Fig.1,the boundary conditions used in the present simulations include inflow,outflow and no-slip,standard boundary conditions for incompressible flow are applied:the velocity is imposed at the inlet and the pressure is fixed at the domain outlet.A no-slip boundary condition is used at both the upper and lower walls.Here,an appropriate grid of dimension is used,as shown in Fig.2,the O type mesh is chosen because of the rounded leading edge.Based on the diameter of the cylinder,a value of Re=1.36×105is used for simulations in computations,and the diameter of the cylinder is 0.02m.
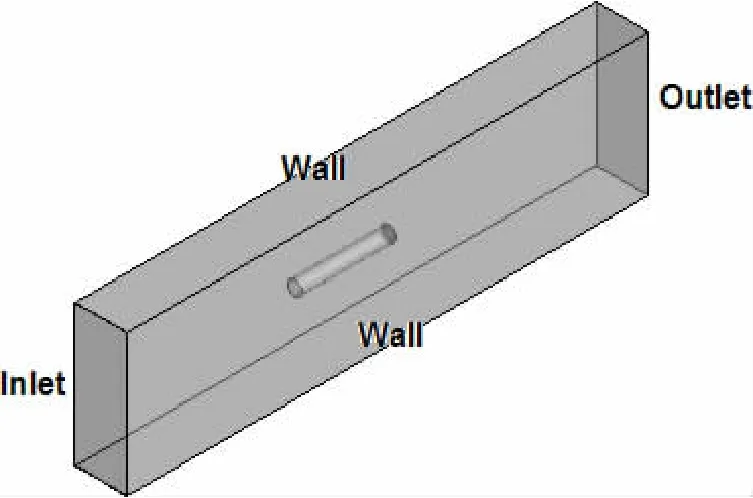
Fig.1 Outline of the computational domain

Fig.2 Computational grids around body
Fig.3(a)and(b)show flowfield snapshots of the steady cavitating flow over a hemispherical axisymmetric body,the contours of volume fraction of vapor phase are shown respectively when the cavitation number is 0.3.For all cases,the presences of the bubble manifest itself as a decrease in magnitude,flattering and length-ening of the pressure minimum along the surface.Also,bubble closure gives rise to an overshoot in pressure recovery due to the local stagnation associated with free-stream liquid flowing over the convex curvature at the aft end of the bubble.But the cavity interfaces captured with different model are noticeable different,in the downstream region of the nature cavity,the cavity interface obtaind by Level set method is sharper.In addition,in the cavitation area,the vapor volume fraction is moderately larger than the results obtained with the mixture model.
Fig.3(c)shows the comparisons between predicted and measured surface pressure distributions in parallel.Both the models match the experimental data satisfactorily.Differences in the performance are more noticeable in the closure region,where the vapor phase condenses.Fig.3(d)shows the corresponding density distribution along the surface.As seen from density plots,the liquid phase first expands and vapor phase appears uniformly inside the cavity,then the vapor phase is compressed,in a shock like fashion,back to the liquid phase.The differences among the two models in density profiles are significant.This implies that each model generates different compressibility characteristics,although they produce very similar steadystate pressure distributions;which model produces the correct compressibility is an open question and needs further investigation.

Fig.3 Contour of volume fraction of vapor phase and density distribution with different models(σ=0.3)(a)Contour of volume fraction of vapor phase with Level set method(b)Contour of volume fraction of vapor phase with mixture model(c)Comparisons between predicted and measured surface pressure distributions(d)Density distribution along the surface with different models
3.2 Unsteady natural cavitation around a Clark-Y hydrofoil
Unsteady nature cavitating flow over the Clark-Y hydrofoil is investigated using the Level set method.In such cavitating case,liquid-vapor mass transfer occurs through local fluctuations about the saturation pressure.Here,the geometry is based on the Clark-Y profiles,has a 0.07m chord,and is twisted a total of 8 degrees.The computational model setup approximates to the experiments of Wang et al[15],simulating the hydrofoil within inviscid wall.In the experiment,the tunnel was run various speeds and pressures,visual comparisons are made with the results at V∞=10m/s,and σ=0.8.
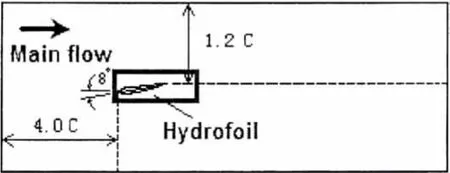
Fig.4 Outline of the computational domain
Fig.5 Computational grids around a hydrofoil
Fig.6 displays comparisons of the unsteady cavity around the Clark-Y hydrofoil between the mixture model and the Level set method,the temporal evolution of the computed and experimentally observed flow structures with cloud cavitation(σ=0.8)is shown.Here,the experimental visual images are shown in Fig.6(a),the black and white images correspond to an instantaneous visualization of one cycle,and Fig.6(b)and(c),show the time sequences of flow structures predicted by different models,the blue color corresponds to liquid and the red color corresponds to a highly concentrated bubble flow.
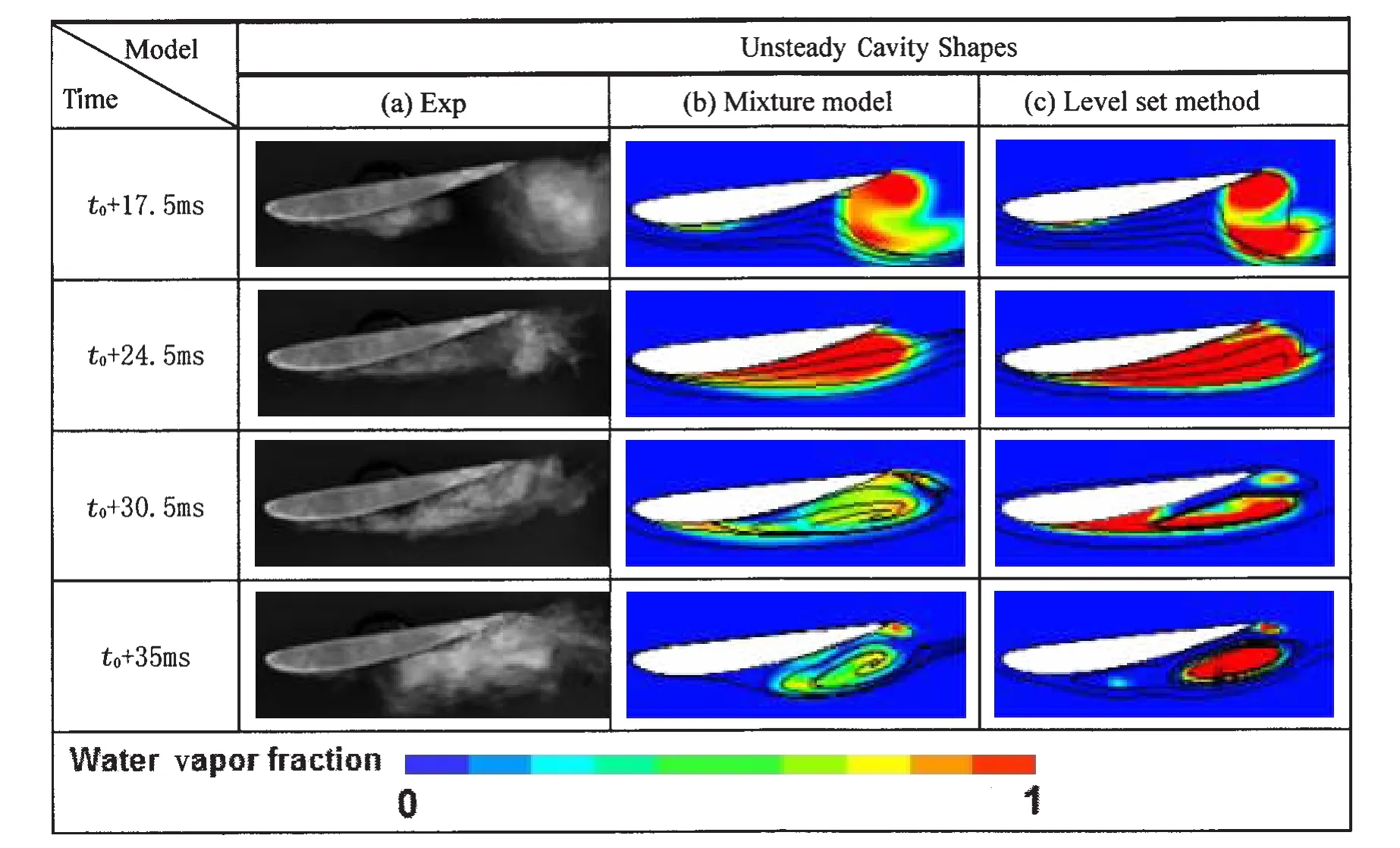
Fig.6 Time evolution of cloud cavitation with the numerical results and experimental visuals
There is a good agreement between the numerical and experimental results concerning the external shape and global structure of both attached cavity and vapor cloud shedding is achieved;but the vapor/water interface and vapor volume fraction with different models are distinct.The cavity got by Level set method is more obvious with larger vapor volume fraction.And also,the Level set method scheme prediction displayed the increased cavity size.This is because,for the Level set method in present study,the anti-diffusive characteristics of this scheme predict the nature cavity with much sharper,and hence it provides crisp interface for both steady-state and transient simulations.
3.3 Axisymmetric ventilated disk cavitor
The case relevant to the cavitating flows is ventilated cavitating flows around an axisymmetric disk cavitator.In this case,liquid flow around the disk and a gas injected into the wake form supercavities.The geometric configuration is displayed below in Fig.7,with the disk positioned such that the flat front is perpendicular to the free-stream velocity vector of a liquid flow.Such a case,where the air gas is injected into a liquid flow to form a cavity,is referred to as artificial or ventilated cavitation,the diameter of disc Dnis 15mm.In numerical simulation,the grid distribution is shown in Fig.8.
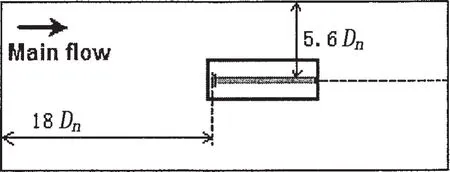
Fig.7 Schematic diagram and computational domain

Fig.8 Computational grid for flow analysis
There are two cases predicted with different multiphase models,the assumed conditions for the cases are:for case-1,U∞=8m/s,and σ=2.37,ventilated rate Q is 400L/h;for case-2,U∞=3m/s,and σ=22.56,ventilated rate Q is 600L/h.
Solution comparisons with and without the Level set method are evaluated in Fig.9.In our computation,the gas volume fraction isosurface 0.8 is defined as ventilated cavity.In both cases,without the interface sharpening of Level set method,the predicted profiles of the ventilated cavity tend to converge on a relatively smaller cavity size to the experimental visualizations and the numerical results obtained by Level set method.Whereas,the scheme with Level set method converges a cavity size shape that is quite similar to experimental photographs.
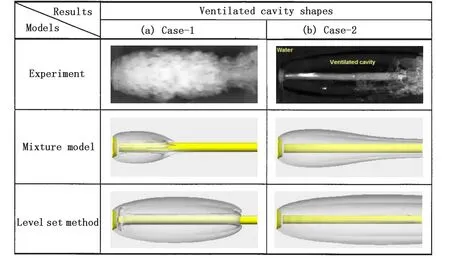
Fig.9 Visual comparisons of the predicted cavities with observations from experiment
Compared with the experimental data,the predicted cavity profiles at different models are examined in Fig.10.The numerical results vividly show significant benefit in the prediction using the free surface sharpening approach,the axial cavity width(Dc)with Level set method are well predicted.As we know,mixture model allows mutual penetration and mixing between different phases,there is large numerical dissipation in vacuoles length and radius of the direction,particularly reflected in the length direction.But,the Level set method includes complete interface features,and with the surface tension model,it is easy to handle diffusion and pulsation characteristics in numerical simulations.
4 Conclusions
In this present study,the Level set method for nature and ventilated cavitating flows are validated,various cases including the steady cavitation around the cylindrical body,unsteady cavitating flow around the Clark-Y hydrofoil and the ventilated cavitating around a disk are presented.Compared with the results obtained by mixture model and experimental visualizations:
(1)For nature cavitating flows,although all three models give satisfactory predictions in overall pressure distributions and unsteady cavity shapes,differences are observed in the closure region of the cavity with the mixture model and Level set method,resulting from the differences in compressibility characteristics handled by each model.The cavity interface obtaind by Level set method is sharper.In addition,in the cavitation area,the vapor volume fraction is moderately larger than the results obtained with the mixture model.
(2)For ventilated cavitating flows,the Level set method modified forms resulted in improved numerical accuracy and the ability to better resolve the cavity shape with the same cells.The scheme with Level set method converging a ventilated cavity size shape is very similar to experimental photographs and data,compared with the results obtained by mixture model.
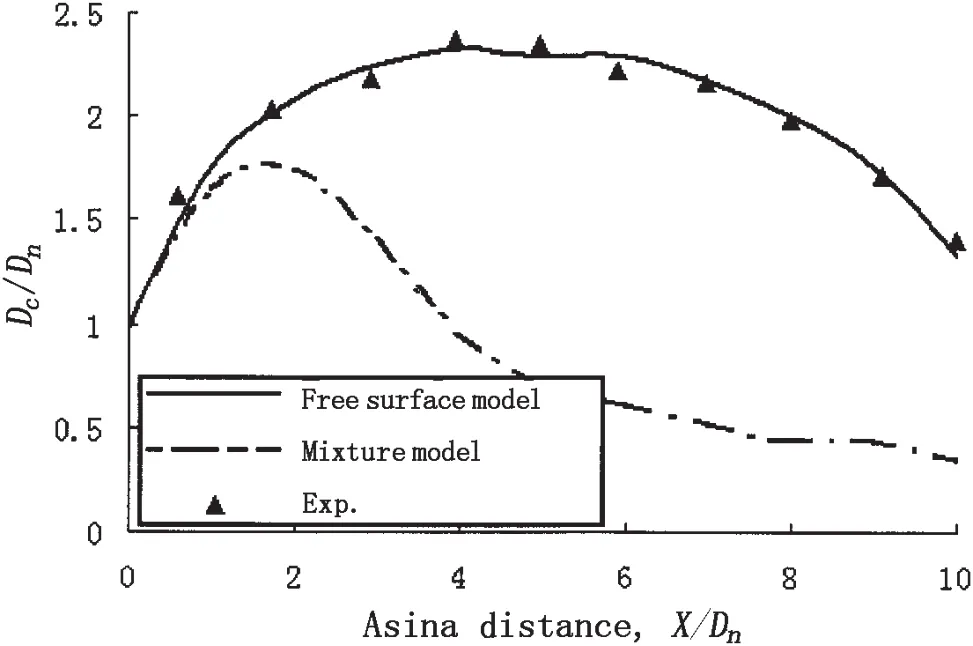
Fig.10 Plots of the cavity radius versus the axial distance
[1]Hart C W,Nichols B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].J Comput Phys,1981,39(1):201-225.
[2]Noh W F,Woodward P R.SLIC(simple line interface calculation)[C]//In:van de Vooren A,Zandbergen P(ends).Proceedings of Fifth International Conference on Fluid Dynamics,59 of Lecture Notes in Physics,Berlin:Springer,1976:330-340.
[3]Ashgriz N,Poo J Y.FLAIR:flux line-segment model for advection and interface reconstruction[J].J compute Phys,1991,93(2):449-468.
[4]Youngs D L.Time-dependent multi-material flow with large fluid distortion[M].In:Morton K W,Baines M J(eds).Numerical Method for Fluid Dynamics,New York:Academic Press,1982:273-285.
[5]Ubbink O,Issa R I.A method for capturing sharp fluid interfaces on arbitrary meshes[J].J Comput Phys,1999,153(1):26-50.
[6]Sussman M,Puckett E G.A coupled Level set and volume-of-fluid method for computating 3d and axisymmetric incompressible two-phase flows[J].Journal of Computational Physics,2000,162:301-337.
[7]Sussman M,Smereka P,Osher S.A Level set approach for computating solutions to incompressible two-phase flow[J].Journal of Computational Physics,1994,114:146-159.
[8]Shu Bitan,et al.Implementation of the Level Set Method into OpenFORM for capturing the free interface in incompressible fluid flows[J/OL].Documentation of OpenFOAM.www.openfoam.com.
[9]Zwart P.Industrial CFD applications of free surface and cavitation flows[R].VKI Lecture Series:Industrial Two-Phase Flow CFD,2005.
[10]Brackbill J U,Kothe D B,Zemach C.A continuum method for modeling surface tension[J].Journal of Computational Physics,1992,100:335-354.
[11]Kubota A,Kato H,Yamaguchi H.A new modeling of cavitating flows:a numerical study of unsteady cavitation on a hydrofoil section[J].J Fluid Mech.,1992,240:59-96.
[12]Menter F R.Zonal two equation k-ω turbulence models of aerodynamics flow[R].AIAA paper 1993-2906,1993.
[13]Strelets M.Detached eddy simulation of massively separated flows[R].AIAA-01-0879,2001.
[14]Rouse H,McNown J S.Cavitation and pressure distribution,head forms at zero angle of yaw[R].Studies in Engineering Bulletin 32,State University of lowa,1948.
[15]Wang G Y,Senocak I,Shyy W.Dynamics of attached turbulent cavitating flows[J].Progress in Aerospace Sciences,2001,37(6):551-581.
[16]Gopalan S,Katz J.Flow structure and modeling issues in the closure region of attached cavitation[J].Phys.of Fluids.2000,12:895-911.
[17]Foeth E J,Vandoorne C W H,Vantersiega T,Wieneke B.Time resolved PIV and flow visualization of 3D sheet cavitation[J].Exp.in Fluids,2006,40:503-513.
[18]Adrian R J.Twenty years of particle image velocimetry[J].Exp.in Fluids,2005,39:159-169.
Level set方法在空化流动计算中的应用
黄 彪,王国玉,张敏弟,陈维清
(北京理工大学机械与车辆工程学院,北京 100081)
文章将Level set方法应用于自然空化与通气空化流动计算中,通过耦合入相间的质量传输方程,建立了一个用于描述气、汽、液多相空化流动的数值模拟方法,分别对绕圆头回转体和Clark-Y型水翼的自然空化流动和绕圆盘的通气空化流动进行了数值模拟研究,并与实验结果进行了对比,研究结果表明:相较常用的多相流模型(mixture model),Level set方法通过时间和空间上的压缩离散方案,减小了相间界面的扩散,准确地捕捉到了相间的界面,可以有效地运用于空化多相流动。
空化流动;混相模型;Level set方法
TV131.32
A
黄 彪(1985-),男,北京理工大学机械与车辆工程学院博士研究生;
陈维清(1985-),男,北京理工大学机械与车辆工程学院硕士研究生。
TV131.32
A
1007-7294(2011)03-0207-10
date:2010-07-24
Supported by National Natural Science Foundation of China(Grant No.50679001 and Grant No.50979004)
王国玉(1961-),男,博士,北京理工大学机械与车辆工程学院教授/博士生导师;
张敏弟(1970-),女,博士,北京理工大学机械与车辆工程学院副教授;
