高速铁路GPS控制网投影变形处理方法的探讨

冯光东 王 鹏

(中铁第四勘察设计院集团有限公司,湖北武汉 430063)

目前,我国正在大规模建设高速铁路,其高速性、高平顺性对测量提出了更高的要求。为指导铁路精测网的建网,2009年铁道部颁布了《高速铁路工程测量规范》，该规范要求控制网的投影长度变形值不大于10 mm/km[1]。为达到投影长度变形不大于10 mm/km,各铁路设计院在实际生产中都采用任意中央子午线、任意高程面的高斯投影处理方法。该方法对南北走向的线路工程比较适合,对东西走向的线路工程,分带过多导致坐标换带计算工作繁琐,施工中容易出错。为此,本文对斜轴墨卡托投影处理方法在高速铁路精测网中的应用进行探讨,对高斯投影和斜轴墨卡托投影两种方法进行了比较分析。

1 任意中央子午线任意高程面的高斯投影处理方法

大地坐标系的椭球面是一个凸起的不可展平的曲面,当采用高斯正形投影将曲面上的元素投影到平面上时,投影后的边长会产生长度变形,这种投影变形主要由高程归化与高斯投影变形改化两方面因素引起,其综合影响公式为[2]

(1)

式中S——地面上的观测长度；

Hm——观测边的平均大地高；

hm——观测边的归化大地高；

Rm——边长地区地球平均曲率半径；

Ym——S在高斯平面上离中央子午线的垂距。

投影改正的相对残差公式为[2]

(2)

投影长度变形不大于10 mm/km,即VS/S不大于10 mm/km。目前,常规的做法是通过选择合适的中央子午线和投影面高程,即通过合理确定式(2)中的Ym和hm,使VS/S不大于10 mm/km。对于不同的高程归化值(Hm-hm),可以计算出相应的离中央子午线垂距Ym的范围,见表1。

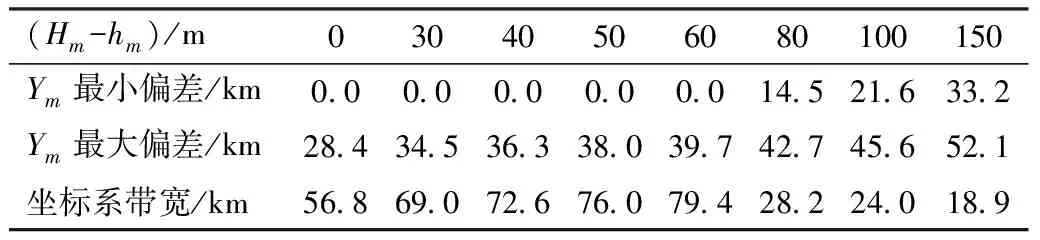
表1 投影长度变形不大于10 mm/km的坐标系带宽统计

由表1分析可知：

当高程归化值(Hm-hm)在60 m以内时,其高程归化改正很小,并能起到抵偿高斯投影变形的作用,使得满足投影长度变形不大于10 mm/km的坐标系带宽最大。

当高程归化值(Hm-hm)大于60 m时,由于高程归化改正增大,其对投影长度综合变形的影响占据主导地位,从而使得在中央子午线附近对高斯投影变形的抵偿作用相对变小,使坐标系带宽变窄。

在实际工程应用中,通常采用构建工程椭球的方法来消除高程归化改正的影响,采用移动中央子午线的方法来消除高斯投影变形的影响。对于南北走向的线路,其东西跨越的范围不大,可采用任意中央子午线、任意高程面的高斯投影处理方法。对于东西走向的线路,其东西跨越的范围较大,由于高斯投影坐标系带宽较窄而使得投影带的数量过多,导致坐标换带计算工作繁琐,为了避免这种问题,可采用斜轴墨卡托投影。

2 斜轴墨卡托投影处理方法

斜轴墨卡托投影亦即斜轴圆柱投影。对于线路控制网,采用斜轴墨卡托投影,使圆柱面与线路中心线相切,并进行投影,从而有效解决长度变形的问题。地球是一个椭球体,用椭球体描述地球进行斜轴墨卡托投影则计算较为困难。为了计算简便,在几百公里的工程范围内可以选用圆球来表示地球,若线路控制网较长,圆球描述地球带来的误差较大,则可以分段处理。为了便于计算,通常斜轴圆柱投影都转换为横轴圆柱投影或正轴圆柱投影。

2.1 斜轴圆柱投影转换为横轴圆柱投影的处理方法

斜轴圆柱投影转换为横轴圆柱投影时,需要对参考圆球进行变换,使线路中心线走向与变换后参考圆球的经线方向一致。

(1)参考圆球的大地坐标

当斜轴圆柱投影转换为横轴圆柱投影时,斜轴圆球一般取线路中心线走向为起始子午线方向。正轴圆球的大地坐标计算式为

(3)

斜轴圆球的大地坐标可以由正轴圆球的大地坐标通过变换得到,此变换需要以球面极坐标为中间过渡坐标。

在以Q点为极点的球面坐标系中,计算出线路上各GPS点的极坐标(α,z),其计算公式可根据球面三角公式推导得到[3-4],即

(4)

式中：(B0,L0)为极点Q在正轴圆球上的经纬度,(B,L)为所求点在正轴圆球上的经纬度,(α,z)为所求点的球面极坐标,方位角α由过极点Q的经线起算,z为极距QT。

假设QT与线路中心线的走向一致,以QT为斜轴圆球的中央子午线,则各GPS点在斜轴圆球上以Q点为极点的极坐标为

(5)

在斜轴圆球上,根据球面三角公式可推导大地坐标的计算公式[3-4],即

(6)

(2)圆柱投影的平面直角坐标

由球面上一点的大地坐标(B′,L′)计算其平面直角坐标的公式为[5]

(7)

(8)

2.2 斜轴圆柱投影转换为正轴圆柱投影的处理方法

斜轴圆柱投影转换为正轴圆柱投影时,需要对参考圆球进行变换,使线路中心线走向与变换后参考圆球的赤道方向一致。

(1)参考圆球的大地坐标

当斜轴圆柱投影转换为正轴圆柱投影时,斜轴圆球一般取线路中心线走向为参考圆球的赤道方向。

斜轴圆球的大地坐标可以由正轴圆球的大地坐标通过变换得到,此变换需要以球面极坐标为中间过渡坐标,变换过程与横轴圆球的大地坐标向斜轴圆球的大地坐标变换相似,不同之处在于线路中心线走向QT与斜轴圆球的赤道重合,则各GPS点在斜轴圆球上以Q点为极点的极坐标为

(9)

斜轴圆球上的大地坐标计算公式见式(6)。

(2)圆柱投影的平面直角坐标

经过正轴圆球大地坐标向斜轴圆球大地坐标的变换,斜轴墨卡托投影已转换为正轴等角切圆柱投影。等角切圆柱投影具备着经线长度比等于纬线长度比,以及圆柱切线处的投影变形等于零等性质。

(10)

对式(10)积分,得[6]

则正轴等角切圆柱投影的平面坐标为[6]

(11)

式中ρ是角度换算为弧度的常数。

由于圆柱面沿线路中心线相切,线路中心线上的长度投影前后保持不变,偏离线路中心线愈远,长度变形愈大；投影前后各点的方向值保持不变。因此,以上两种斜轴墨卡托投影对线路工程的测量极具意义。

3 算例分析与比较

以一个实际工程控制网算例进行试算分析,比较斜轴墨卡托投影处理方法与任意中央子午线、任意高程面的高斯投影处理方法的差异。

试算数据采用某段高速铁路CPⅠ级GPS控制网数据。该段GPS控制网全长约190 km,位于东经109°38′～121°20′,北纬31°09′～32°02′之间,见图2。

如图2所示,该段线路GPS控制网呈东南—西北走向,若采用任意中央子午线、任意高程面的高斯投影处理方法,则该段线路GPS控制网至少划分3个投影带，才能达到投影长度变形不大于10 mm/km；若采用斜轴墨卡托投影处理方法,由于GPS点离线路中心线较近,则不需要进行分带投影处理,在一个坐标系内就能达到投影长度变形不大于10 mm/km。下面将采用这两种不同投影处理方法进行计算比较。

3.1 计算方案

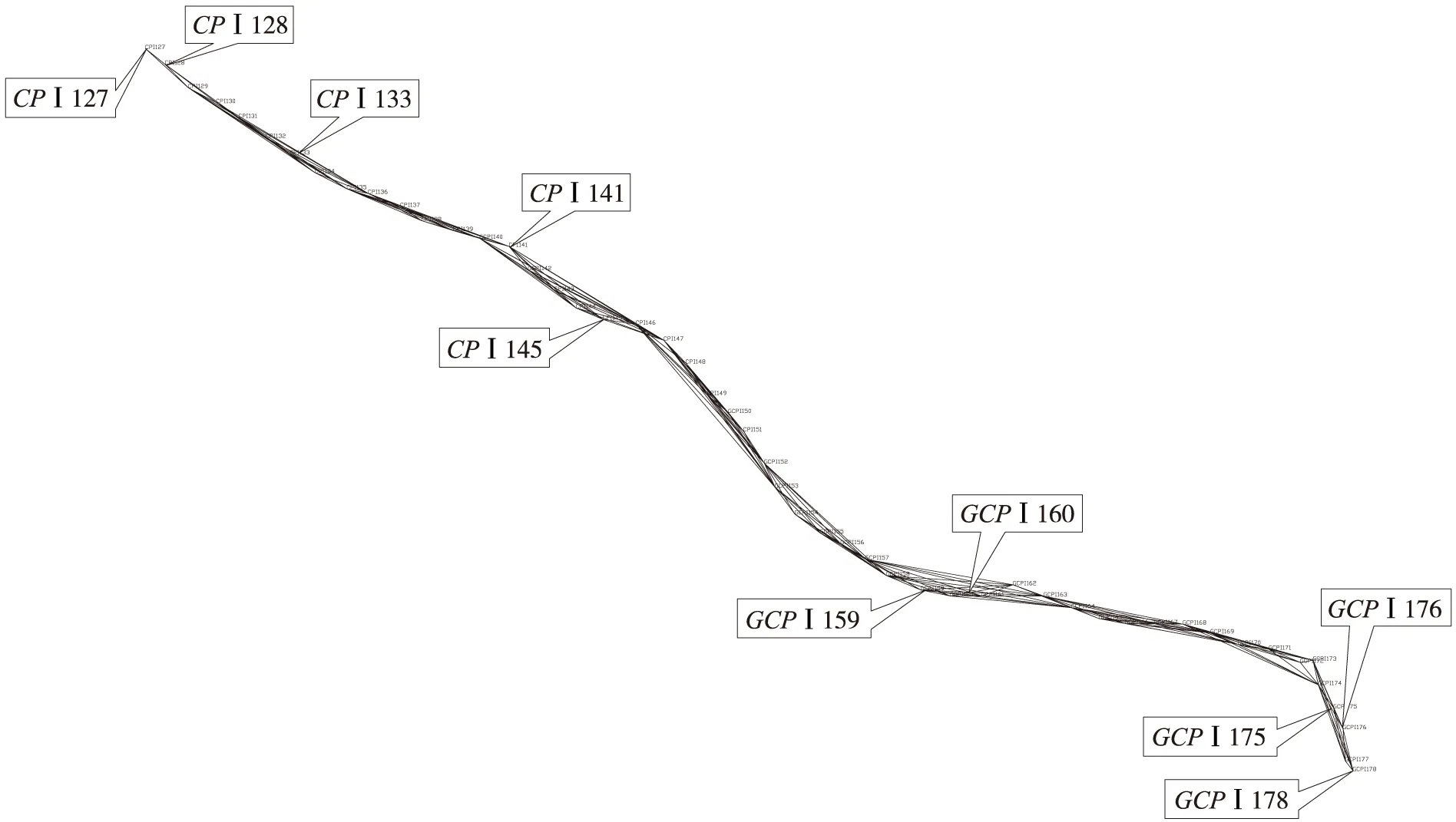
图2 某段高速铁路CPⅠ级GPS控制网示意

基线解算完成后,在其三维基线向量的成果基础上,完成下述后续计算：

以点GCPⅠ159的A级GPS基站网基站成果,在WGS-84坐标系中,对GPS网进行三维无约束平差,检测GPS基线向量网本身的内部精度以及可能存在的粗差。

以点CPⅠ128、CPⅠ141、GCPⅠ159、GCPⅠ176的A级GPS基站网基站成果,在WGS-84坐标系中进行三维约束平差。

根据投影长度变形不大于10 mm/km的要求,对该段线路GPS控制网进行投影带的划分及投影面高程的选择,并计算各GPS点的高斯平面直角坐标及投影变形系数,根据投影变形系数划分投影带。投影带的划分及投影面高程的选择结果见表2。

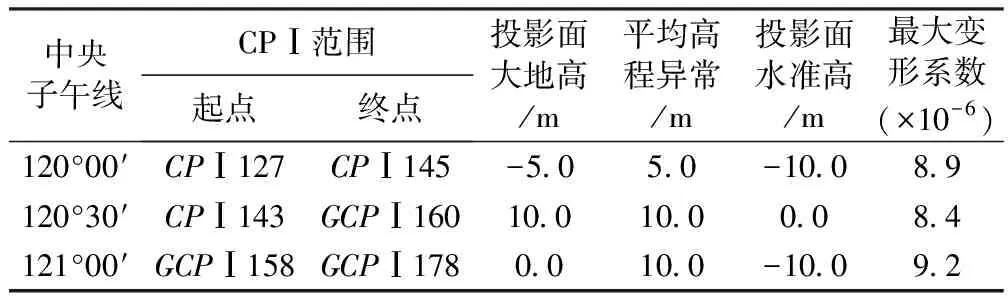
表2 投影带划分、投影面高程选择统计

取沿线路分布较为均匀,且大地高与线路平均高程面较为接近的点CPⅠ133、CPⅠ145、GCPⅠ160、GCPⅠ175作为参考圆球的拟合点,以点CPⅠ127至GCPⅠ178作为线路中心线的走向，进行斜轴墨卡托投影处理。

3.2 计算结果分析

按照上述计算方案对数据进行计算,其计算结果分析如下：

对于线路GPS控制网,通过选择合适的中央子午线和投影面高程,采用高斯分带投影处理方法,可以达到投影长度变形不大于10 mm/km的要求；但存在高斯投影坐标带宽较窄,投影带的数量过多,投影带边缘变形较大等问题,见图3。

图3 高斯投影变形系数统计

通过球面拟合使参考圆球与测区地面达到最佳吻合,采用线路中心线与投影圆柱面相切,从而使投影长度变形控制在较小的范围内；对于该段线路GPS控制网,可使投影长度变形小于2 mm/km,见图4。

图4 斜轴墨卡托投影变形系数统计

将高斯投影处理与斜轴墨卡托投影处理得到的平面边长进行比较,其比较结果均小于10×10-6,除了高斯投影带边缘,其他地区的均小于3×10-6,说明两种投影处理方法得到的平面边长是基本吻合的,差异较大的边长产生的原因主要是由于高斯投影变形引起的,其分布规律与高斯投影变形相关。

4 结 论

斜轴墨卡托投影的参考圆球是通过沿线路分布较为均匀且大地高与线路平均高程面较为接近的点最佳拟合出来的,其参考圆球面与测区地面达到最佳吻合,缓解了由高程归化引起的变形；投影圆柱面沿线路中心线相切,使得各GPS点离投影中心线较近,缓解了由圆柱投影引起的投影变形。综上所述,对于线路GPS控制网,特别是高速铁路GPS控制网,在保持边长投影与地面网的边长尺度一致方面,斜轴墨卡托投影比高斯投影更加适用。

[1]中铁二院.TB10601—2009 高速铁路工程测量规范[S].北京:中国铁道出版社,2009

[2]董鸿闻,李国智,陈士银，等.地理空间定位基准及其应用[M]. 北京:测绘出版社,2004

[3]吴忠性,杨启和.数学制图学原理[M].北京:测绘出版社,1989

[4]李汝昌,王祖英.地图投影[M].武汉:中国地质大学出版社,1992

[5]沙月进,高洪兴,胡伍生.斜圆柱投影方法及其在交通工程中的应用研究[J].公路交通科技.2004,21(11):20-22

[6]谭祥林.斜轴等角切圆柱投影[J].测绘通报.1960(6):21-24