MIMO系统中基于平均PER 约束的跨层设计

周婷婷，刘晓帅，杨 颖，殷 馨

（南京航空航天大学电子信息工程学院，江苏南京 210016）

0 引言

在未来的移动通信网络中，无线链路在保证业务服务质量（quality of service，QoS）前提下，需要提供更高的传输速率;但无线链路的衰落特性限制了其传输能力［1］。为了提高无线数据通信系统的性能，利用多层相互协调的跨层设计已经成为当前的研究热点。文献［2］提出了单输入单输出（single input single output，SISO）瑞利衰落信道下，联合自适应编码调制和自动重传请求（automatic repeat request，ARQ）协议的跨层设计。文献［1，3-5］均提出结合空时分组编码（space time block coding，STBC）［6］的多输入多输出（multiple inputmultiple output，MIMO）系统的跨层设计。然而，在上述文献的跨层设计中，物理层自适应调制（adaptive modulation，AM）的门限选择都是基于瞬时误包率（packet error rate，PER）的约束条件，这样做虽可能会简化问题分析，但这种严格的约束条件将会导致系统频谱效率（spectral efficiency，SE）牺牲过多。为此，需要考虑采用基于平均PER约束条件的AM，以期实现满足目标PER要求的同时，大大提高系统SE。Torrance等［7］首先提出AM的门限优化算法，即通过最小化一定的代价方程（即平均误码率（bit error rate，BER）和平均频谱效率（average spectral efficiency，ASE）与目标值的差值）来搜索最优门限值。文献［8-9］提出了采用Lagrange优化方法以最大化ASE求得最优自适应门限，其解同样需要通过计算机数值搜索。此外，文献［10］给出了一种Two-mode方法来优化门限值，该方法实质上是Torrance方法的变型，仍然采用Torrance提出的代价方程，只是每次仅考虑相邻2种调制方式。在这些优化方法中，Torrance方法与Lagrange方法类似，只是在代价函数中以不同的形式来表示平均BER约束条件。文献［11］将Lagrange方法下的优化门限应用于单载波和多载波系统的性能分析中，以表明此门限的优越性，其结果表明可获得较高的SE。然而，上述文献仅针对物理层自适应调制的门限优化，没有考虑跨层的优势，使得SE提高有限。

基于上述分析，本文将在已有文献的基础上，给出平均PER约束下联合物理层AM和链路层ARQ的跨层优化设计，并利用Lagrange乘子法对平均PER约束条件下的门限优化问题进行建模。针对此优化问题，采用简化Newton法求解，可有效地避免原有文献需要通过大量的数值搜索来求解。在此基础上，利用获得的优化门限，分析MIMO系统结合STBC和跨层设计的性能，给出系统平均PER和ASE的理论计算。其结果表明，与瞬时PER约束下的系统跨层方案相比，基于平均PER约束的系统跨层方案可以在满足一定PER要求时获得较高的系统SE。

1 系统模型

这里考虑物理层是有Nt个发射天线和Nr个接收天线的无线MIMO通信系统，工作于平坦准静态瑞利衰落信道。该信道用Nr×Nt维矩阵 H=［hi，j］Nr，Nti，j=1来表示，其元素 hi，j为从第 j个发射天线到第i个接收天线的信道增益。由于信道是准静态的，hi，j在一帧（对应于K个时隙）内保持不变，但在不同的帧之间则独立变化。对于瑞利衰落，hi，j可建模为独立同分布均值为0，每维方差为0.5的复高斯随机变量，即 hi，j～ CN（0，1） 。由文献［12］可知，系统输入输出信号关系为

（1）式中，Y是Nr×K维接收信号矩阵;X是输入符号经过空时编码后的Nt×K维发送信号矩阵;N是Nr× K 维噪声矩阵，其元素 ni，j～ CN（0，σ2n） 。

假设来自Nt个发射天线的平均发射功率是Pt，则每接收天线下平均信噪比为STBC的编码矩阵G是由输入的L个符号映射成K个时隙的Nt维矢量组成的Nt×K维矩阵，其码率Rc为L/K。利用STBC的复正交性［6］，系统在译码后的L×1维信号矢量y可表示为［12］

（2）式中，c是与STBC有关的常数，x=［x1，…，xL］T表示输入符号序列，其每个元素的平均功率均为为Frobenius范数;v为L×1维噪声矢量，且其元素vi～从而，可以得到空时译码后的瞬时接收信噪比为由服从自由度为2κ（ κ =NtNr）的非中心卡方分布，利用随机变量的变换可以得到 γ 的概率密度函数（PDF）［3，12］为

（3）式中，Γ（·）为伽马函数。

假设MIMO系统接收端通过信道估计可以获得完全信道状态信息（channel state information，CSI），该CSI一方面用于信号检测，另一方面则通过反馈链路实时传给发送端进行AM，同时也反馈给链路层的ARQ控制器，控制器在保证系统QoS的情况下决定重传的次数，并将此反馈给发送端来调整重传。为了减少传输时延，链路层采用受限ARQ技术，即系统给定最大请求重传次数，当重传次数到达时，发送的数据包仍然不能正确接收则被丢弃。

2 系统性能

在进行跨层设计时，假定链路层允许的丢包率（packet loss rate，PLR）不高于Ploss。根据最大重传次数的限制，物理层的目标PER可表示为由文献［2］可知，调制方式n在加性高斯白噪声信道下近似PER为

（4）式中，参数 {an，gn，γpn} 由调制方式 n决定，其具体值可参见文献［2］中的表I。

系统平均 PER［2］可以表示为

（5）式中:N为调制方式总数;Rn=Rc·lb（Mn）;Mn为星座图大小;假设调制方式n的转换门限值为γn，则 其 对 应 的 平 均 PER 为是调制方式 n 的选取概率，其值可表示为

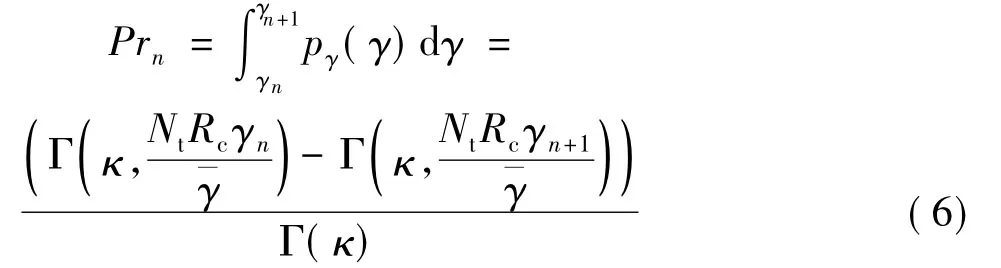
因此，使用受限ARQ后系统ASE为

3 自适应调制门限

利用PERn（γ）=Pobj可获得基于瞬时PER约束条件的自适应调制转换门限值［2］为

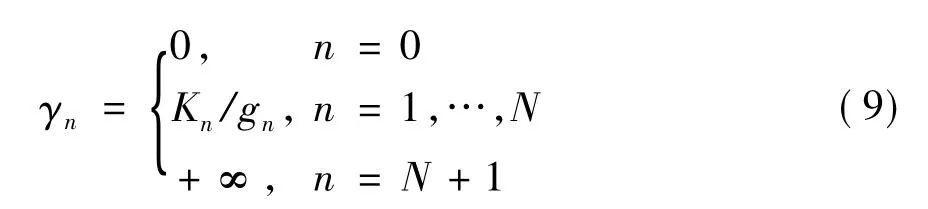
由（9）式获得的门限值可保证每时刻的PER都能满足目标要求，但这种严格的要求使得门限值不能根据信道信息进行自适应优化（即门限值是固定的），其结果将不可避免地带来系统SE的损失。为此，本文将考虑平均PER约束条件下的门限值优化，以期SE得到有效提高，具体为:在平均PER满足目标值Pobj的条件下，通过最大化系统ASE来优化自适应门限。相应的优化目标问题［8］可表示为

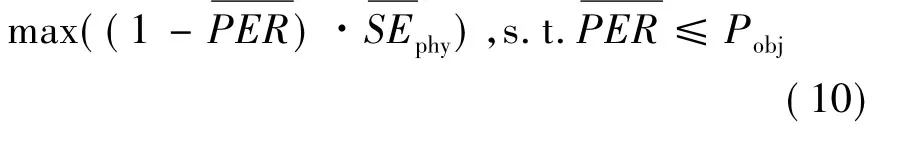
采用Lagrange乘子法构建此门限优化问题为

（11）式中，λ是Lagrange乘数因子。

通过对（11）式的γn（n=1，…，N）求偏导数并令其等于0，即，可得到反映γn之间关系的表达式

（12）式中，由（11）式和Pobj＜1可以看出λ≠1。

采用文献［13-14］的简化Newton算法对（12）式求解，可获得如下关系式

（13）式中:β（k）和 γ（k）= ［γ1，γ2，…，γN］T分别为第k次迭代时计算得到的中间矢量和门限值矢量;F（γ（k））和其Jacobi矩阵DF（γ（k））分别表示为

对（13）式进行求解时，选取有效初值γ（0）使得系数矩阵DF（γ（0））非奇异，且以后各次的迭代均用此系数阵，大大减少了求解次数。此外，也可以通过基于混沌初值的简化Newton法［14］求解出尽可能多的解，再根据条件筛选出有效解。

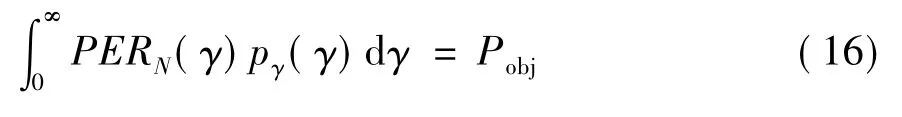
4 性能仿真分析

本节将利用所推导的理论公式和相应的仿真来评估平均PER约束条件下MIMO系统的跨层设计方案性能，并与基于瞬时PER约束条件的系统性能相比较。物理层中自适应调制采用常见的BPSK，QPSK，16QAM，64QAM 4种调制方式，调制速率分别为对应的选择门限假定链路层的目标PLR为10－3。不同的STBC应用于MIMO系统，如G2码、G3码等。在仿真图1－3中，“x T y R（z）”表示x个发射天线和y个接收天线的MIMO系统，并采用STBC中的z码来实现。

图1—图2给出了不同天线数下，系统ASE的理论分析和对应的仿真曲线，其相一致说明了理论公式的有效性。在图1中，假定为2，由图1可知在有效信噪比范围（¯γ≤¯γa）的大部分区域内，平均PER约束下的系统ASE相对于瞬时PER约束下的ASE均有所改善;而在信道条件较差和很好的情况下改善不明显，在低信噪比时，系统PER较高，只能采用低阶调制方式，进而导致2种约束条件下的系统传输速率均很低;而在高信噪比时，瞬时PER约束下的系统可采用高阶调制方式，使传输速率趋于最大，这类似于平均PER约束下最大化系统ASE。由于2发天线系统的高分集度，使2发1收的ASE要高于单天线系统;同时，由图2所示的平均PER约束下2发2收系统也好于非全速率的3发2收系统。由图2还可看出，在平均PER约束下的随着的增大逐渐减小，这与（14）式中与Pobj的关系相一致;当到达阈值时，系统将只采用最高阶调制方式进行调制，传输速率为Rn=6Rc，其中G2，H3和G3码的编码速率分别为Rc={1，0.75，0.5}。图3给出了Nmaxr为2时，2发1收和4发1收天线系统在，2种约束条件下系统平均PER和平均PLR的理论分析和相应的仿真曲线，可以看出，理论和仿真相一致，验证了理论分析的有效性;同时，在有效信噪比范围内，平均PER约束条件下各天线系统的PER和PLR均能满足系统要求的目标值。

图3 不同天线系统的平均误包率和平均丢包率Fig.3 Average PER and average PLR with different antenna systems

5 结束语

本文给出空时编码MIMO系统中一种基于平均PER约束的跨层设计方案，该方案以最大化系统ASE为目标，通过平均PER受限于目标PER进行自适应门限优化。基于Lagrange乘子法，对此门限优化问题建模，并采用简化Newton法进行求解，获得较为简单的数值计算，避免了已有自适应门限优化方案中需要大量的计算机搜索。基于获得的理论结果，利用推导出的平均PER和ASE闭式表达式对系统进行了性能分析。仿真结果表明，所提跨层设计方案可在满足目标PER的情况下获得SE的有效提高，避免了通常基于瞬时PER约束的跨层设计方案所带来的SE损失。而且所给出的理论分析也是有效的，与实际的仿真结果非常相近。

［1］MAAREFA，AISSA S.Combined adaptivemodulation and truncated ARQ for packet data transmission in MIMO systems［C］//IEEE.IEEE Global Telecommunications Conference.Dallas，USA:IEEE Press，2004:3818-3822.

［2］ LIU Qing-wen，ZHOU Sheng-li，GIANNAKISG B.Crosslayer combining of adaptive modulation and coding with truncated ARQ over wireless links［J］.IEEE Transactions Wireless Communications，2004，3（5）:1746-1755.

［3］ MAAREF A，AISSA S.A cross-layer design for MIMO rayleigh fading channels［C］//IEEE.IEEE Technology Driving Innovation-Canadian Conference on Electrical and Computer Engineering.Ontario，Canada:IEEE Press，2004:2247-2250.

［4］LU Xiao-feng，ZHU Guang-xi，LIU Gan，et al.A crosslayer design over MIMO rayleigh fading channels［C］//IEEE.International Conference on Wireless Communications，Networking and Mobile Computing.Wuhan，China:IEEE Press，2005:50-53.

［5］郭丽丽，岳殿武.时延反馈下的自适应STBC-Beamforming跨层设计［J］.北京邮电大学学报，2008，31（6）:85-89，108.

GUO Li-li，YUE Dian-wu.Adaptive STBC-Beam forming Cross-Layer Design under Outdated Feedback［J］.Journal of Beijing University of Posts and Telecommunications，2008，31（6）:85-89，108.

［6］ TAROKH V，JAFARKHANI H，CALDERBANK A R.Space-time block coding for wireless communica-tions:performance results［J］.IEEE Journal on Selected Areas in Communications，1999，17（3）:451-460.

［7］ TORRANCE JM，HANZO L.Optimisation of switching levels for adaptive modulation in slow rayleigh fading［J］.Electronics Letters，1996，32（13）:1167-1169.

［8］ CHUNG ST，GOLDSMITH A J.Degrees of freedom in adaptivemodulation:a unified view［J］.IEEE Transactions on Communications，2001，49（9）:1561-1571.

［9］CHOIB J，HANZO L.Optimum mode-switching assisted adaptive modulation［C］//IEEE.Global Telecommunications Conference.San Antonio，USA:IEEE Press，2001:3316-3320.

［10］ LAIL S，YEH C P，CHANGW T.Switching level optimization for adaptivemodulation［C］//IEEE.IEEE 59th Vehicular Technology Conference.Milan，Italy:IEEE Press，2004:1251-1255.

［11］ CHOIB J，HANZO L.Optimum mode-switching-assisted constant-power single-and multicarrier adaptive modulation［J］.IEEE Transactions on Vehicular Technology，2003，52（3）:536-560.

［12］MSSREF A，AISSA S.Rate-adaptive M-QAM in MIMO diversity systems using space time-block codes［C］//IEEE.IEEE 15th International Symposium on Personal，Indoor and Mobile Radio Communications.Barcelona，Spain:IEEE Press，2004:2294-2298.

［13］刘长安.数值分析教程［M］.西安:西北工业大学出版社，2005.

LIU Chang-an.Numerical Analysis Tutorial［J］.Xi'an:Northwestern Polytechnical University Press，2005:270-273.［14］刘健，袁建平.一种求解非线性方程组的混沌算法［J］.哈尔滨商业大学学报，2001，17（1）:31-34.

LIU Jian，YUAN Jian-ping.A kind of chaotic algorithm for solving nonlinear equations［J］.Journal of Harbin U-niversity of Commerce，2001，17（1）:31-34.