基于瞄准点排布模型的多发同时弹着射击诸元解算＊

2011-06-06石章松王航宇

舰船电子工程 2011年11期

程恭石章松王航宇

（海军装备部1）北京 100036）（海军工程大学2）武汉 430033）

1 引言

大口径舰炮武器系统是舰载攻防体系中重要的组成部分，承担着对岸火力支援、对海攻击、信息对抗和快速应对各种冲突的作战任务。为了弥补由于目标特性辨识复杂和我舰侦察定位系统精度不高等方面的不足，提高对目标的首群毁伤能力与射击效力，从上世纪80年代末提出了“单炮多发同时弹着”（MRSI：multiple rounds simultaneous impact）的新型舰炮作战样式。该作战样式能在不增加兵力的条件下，使最初炸点密度成倍增加，大大提高了舰炮的突然性、猛烈性和毁伤程度，扩大火力毁伤覆盖面，提高单位区域内毁伤火力密集度，被誉为“战斗力倍增法”［1～3］。

针对多发同时弹着射击的诸元计算问题，本文从单炮多发同时弹着的火控机理出发，建立瞄准点排布模型和射击诸元计算模型，并进行了仿真计算，得到相应的射击诸元序列。

2 单炮序列发射同时弹着的火控机理问题描述及计算模型

2.1 火控机理问题描述

确定目标散布及位置信息从而进行火控解算是火控机理问题研究的两个方面，而火控解算问题又是火控机理研究的核心。本文在目标散布及方位已知的前提下，重点研究火控解算问题。火控解算的目的是得到射击诸元参数序列，进而给舰炮武器系统输入射击参数。作为舰炮武器作战样式的一种，其整个作战流程都与舰艇的作战系统息息相关，作战系统实现单炮多发同时弹着工作过程如图1所示［1］。

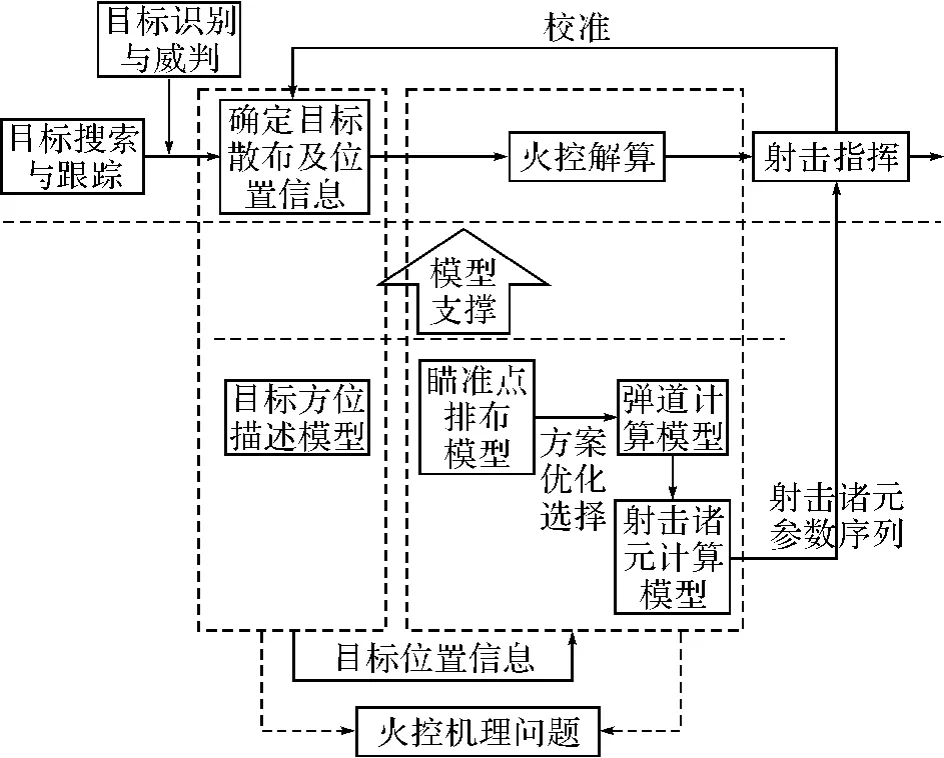
图1 单炮序列发射同时弹着工作流程

2.2 瞄准点排布模型

所谓瞄准点排布，就是指舰炮在基本明确目标所在位置后，采用的一种面积杀伤的落点作战样式，瞄准点以估计的目标方位点为中心，同时弹着的射弹数按照一定的排布规则均匀分布于目标方位点周围，造成对目标的面积杀伤，如图2所示。这种作战样式体现了多发同时弹着的打击特点，从而能够对机动性、隐蔽性比较强的目标，较大概率的打击。

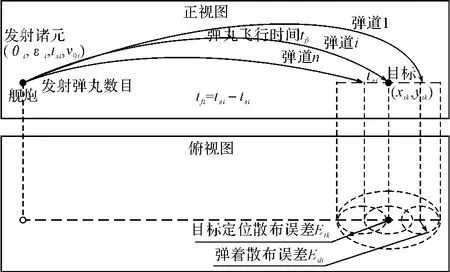
图2 多发同时弹着瞄准点排布模型示意图

为了今后应用于实际作战的方便，根据同时弹着射弹数量，本文给出该情况最简单的瞄准点的排布规则，建立多发同时弹着的瞄准点排布模型。

1）建立瞄准点的排布规则

为了体现其方便应用的特点，选取瞄准点的规则主要有以下3点：

（1）均匀分布原则，即各个瞄准点与目标散布中心的直线距离相等；

（2）求取各个弹丸射击诸元简单，使瞄准点尽量在正北（南）或正东（西）方向上；

（3）炮位点与目标散布中心均在同轴正方向上。

2）建立瞄准点排布模型

基于以上三条原则，给出一种最简单的瞄准点排布规则如图3。

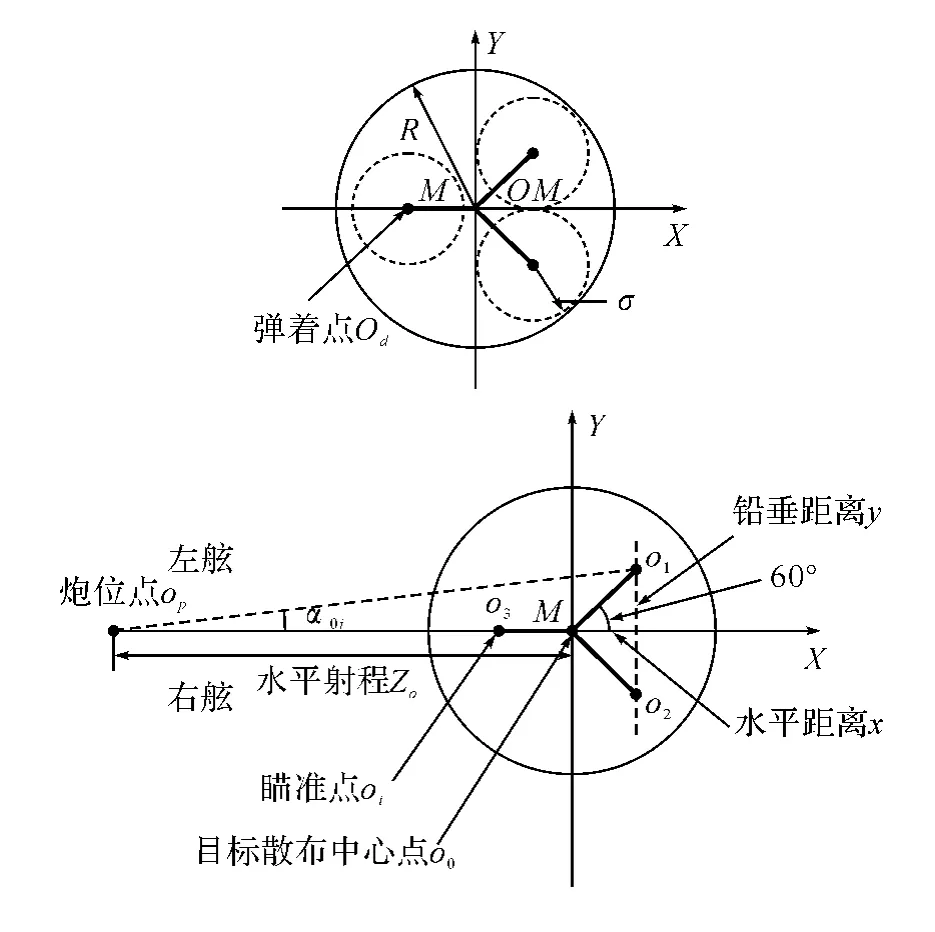
图3 弹着数分别为3发时的瞄准点排布规律

2.3 目标散布中心点与瞄准点的距离M的计算模型

目标散布中心点与瞄准点之间距离M的计算是在已知圆目标首群命中概率后，根据在一定圆目标首群命中概率下，求取瞄准点排布模型的打击目标系统误差m（即目标散布中心与瞄准点的距离M）。

当射击误差为圆目标，系统误差为m，均方差为σ时，圆目标中心O不再与散布中心O′重合，圆目标半径为R，如图3所示。根据概率论知识，瞄准点对目标中心的偏差量服从莱斯分布［6］，分布密度为：

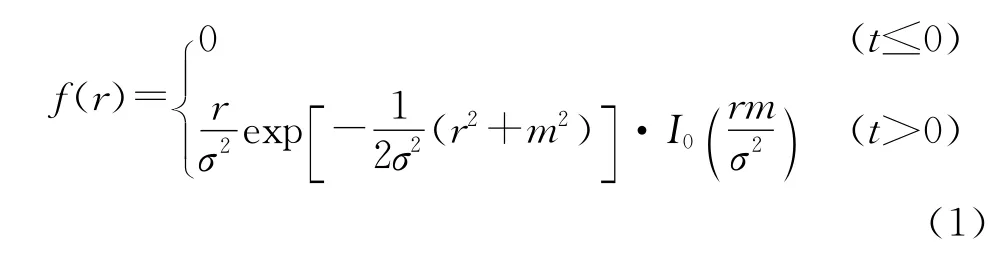
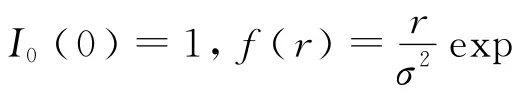
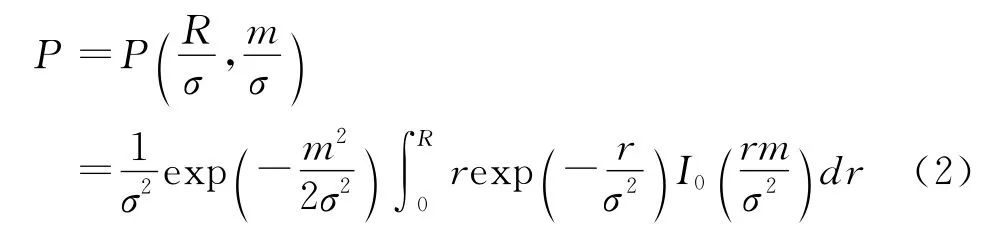
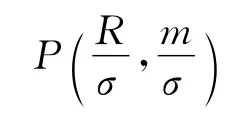
当P已知的情况下，就可以通过插值的方法，得到目标散布中心点与瞄准点距离M。

2.4 质点弹道微分方程组模型

在弹道解算过程中，综合考虑计算精度和计算时间因素，采用如下的弹道方程形式［7～8］：

式中：（Fx2，Fy2，Fz2）为作用在弹丸上的合力在弹道系中的投影；（Mξ，Mη，Mζ）为作用在弹丸质心上的合力矩在第一弹轴系中的投影；（ωξ，ωη，ωζ）为弹丸总的转动角速度→ω在第一弹轴系中的投影。

2.5 射击诸元解算流程

利用质点弹道微分方程组模型，计算得到在相应的装药等级和射角变化范围下射程集合。根据所得的射程集合以及数值分析方法，解算出的相应射击诸元序列，从而实现多发弹丸同时弹着。通过解算质点弹道微分方程组，嵌入线性插值算法，最终得到射击诸元序列（v0i，θ0i，α0i，t0i），相应的射击诸元计算流程如图4所示。

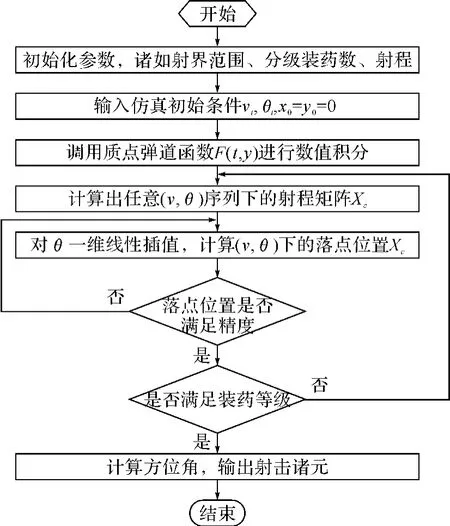
图4 射击诸元解算计算流程

3 计算结果及结论

基于瞄准点排布模型（目标散布中心点与瞄准点不重合），在不同的命中概率的情况下，计算相应的序列射击诸元参数序列表（v0i，θ0i，α0i，t0i），其初始条件为：初速v0i划分600m／s～900m／s，均匀分成7个等级；射角θ0i变化范围（或舰炮射界）：5°～85°，均匀分成50间隔；我舰炮位在二维平面上距离和高度方位x0＝y0＝0；炮口指向左舷为负，右舷为正［1，9～10］。

1）目标散布中心点与瞄准点的距离M的计算

在已知首群命中概率Pn且目标散布半径R＝150m，射弹散布半径σ＝75m的情况下，首先计算不同瞄准点排布规则的目标散布中心点与瞄准点的距离M，如表1所示。

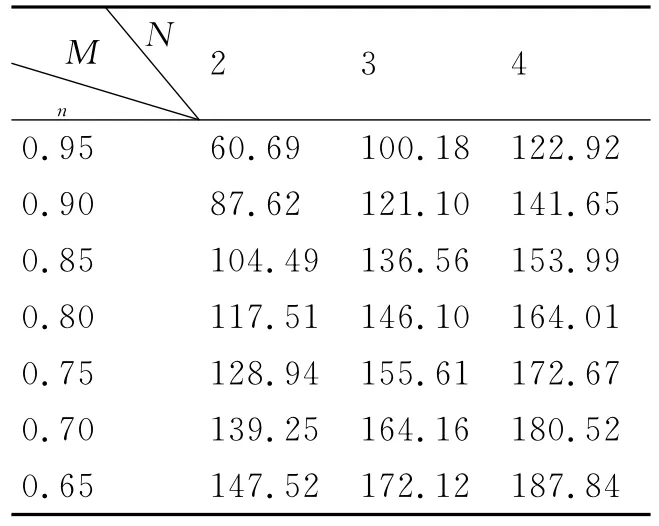
表1 不同瞄准点排布规则的目标散布中心点与瞄准点的距离

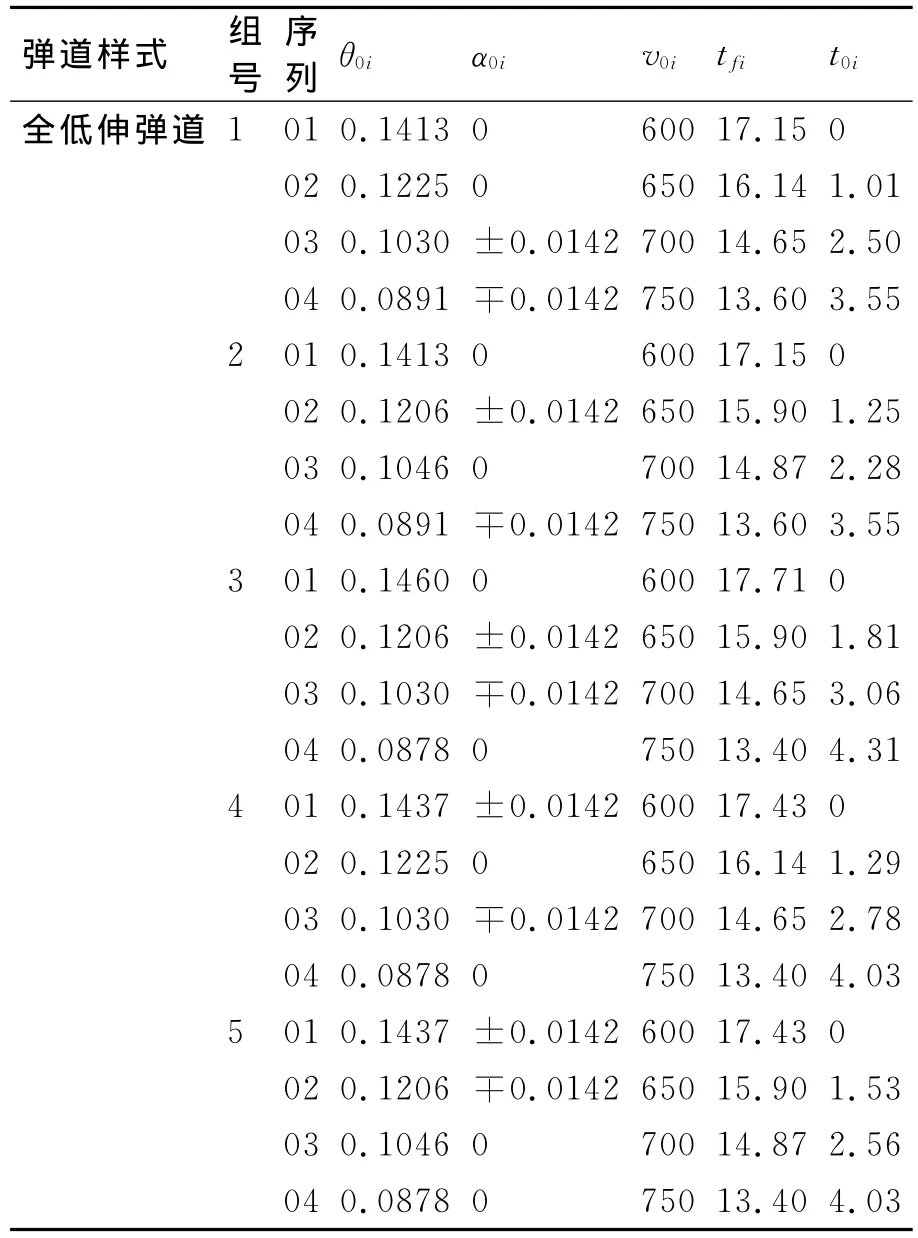
表2 N＝4时瞄准点排布射击诸元参数序列（Pn＝0.90，M＝141.65）

从表1可知，当同时弹着数相同时，随着命中概率的增大，目标散布中心点与瞄准点的距离M越小，打击目标的准确度就会越高、对于武器系统整体性能的要求也就越高；当同时弹着数不同时，射弹数量越多，在相同命中概率条件下，目标散布中心点与瞄准点的距离M就会越大，即对于打击目标的准确性要求就会相应降低。因此，在实际作战中，如果采用瞄准点排布的同时弹着作战样式，同时弹着数是与舰炮本身性能有很大关系，指挥员应该选择合理的同时弹着数，以实现最优的作战效果。

2）瞄准点排布模型射击诸元参数序列计算

根据表1计算的不同瞄准点排布规则的目标散布中心点与瞄准点的距离M和关于射击诸元参数序列的计算方法，在初始条件下，计算射程Z0＝10000m、目标指示精度σ＝75m、目标散布半径R＝150m时的瞄准点排布模型的射击诸元参数序列表（Pn＝0.90），火控解算精度δ≤5m、飞行时间间隔ΔT飞min＞1s，如表2所示，其中α0i为方位角。