某库岸滑坡在水库运行条件下稳定性的动态变化

贾 逸,任光明

(成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)

0 前 言

水库蓄水及水位涨落会改变库区环境工程地质条件,对库岸边坡稳定性的影响主要表现在两个方面[1]:①水库蓄水后抬升岸坡地下水位,导致滑坡体浸水体积增加,弱化部分滑带物理力学性质,降低其抗剪强度,减小阻滑力;②库水位消落时,岸坡岩土体内孔隙水压力消散速度滞后于库水位降低速度,形成朝向坡外的水压力导致下滑力增加。库水位的升降影响水库区涉水边坡的稳定性,如三峡水库自蓄水至135 m以来,库区2000余处涉水滑坡中有300余处发生不同程度的变形破坏,其中60%以上发生在库水位消落期[2]。

库岸边坡是一类常见的非饱和边坡,滑坡体浸润线以上和以下分别处于非饱和与饱和状态。由于水库调度运营,坡外库水位在涨落时波动较大,导致其孔隙水压力场的动态变化,进而影响到岸坡的稳定。部分坡体的饱和与非饱和状态的转变,非饱和区及饱和区水的运动相互联系,将两者统一起来,即所谓饱和与非饱和问题。水位变化触发边坡失稳的现象已经引起国内外岩工程地质和土工程界的重视和兴趣。已有大量文献资料对库水位上升对滑坡稳定性的影响[3-6]、库水位下降对滑坡稳定性影响[7-12]以及库水位的波动对滑坡稳定性的影响[13-17]进行了深入的研究。

某滑坡位于甘肃省白龙江某水电站库区,蓄水前河水位为628.4 m,正常蓄水位为704.0 m,汛期水位为694.0 m。水库运行后,水位在694.0 m～704.0 m之间变动,使其前缘坡体淹没于库水中。水对滑体、滑带的软化作用以及水位变动时产生的孔隙水压力场变化,均对滑坡的稳定性产生一定的影响。本文基于非饱和渗流理论[18],采用近年来广泛使用的限元法[19-20],根据水库调度时可能采用的水位升降速率控制范围,对岸坡在库水位上升和下降情况下进行非稳态渗流和稳定性的耦合分析,以评价滑坡在水库运行期间的稳定性。

1 滑坡基本条件

1.1 地形地貌

滑坡位于某水电站大坝上游5 km的白龙江左岸,形态呈弧形凸向白龙江。该库岸段为侵蚀堆积河谷地貌,地形坡度 20°～35°,两侧为大冲沟切割,后缘为基岩陡壁,远望为典型的滑坡地貌。滑坡前缘高程约为640 m,后缘高程约为1240m,前后缘高差约为600 m。滑坡体纵向长约1400 m,其后缘窄,从中部开始变宽,前缘最宽,自上而下纵观呈一“喇叭状”,见图1,平面面积约0.8 km2,总方量约 3250×104m3,属特大型滑坡。

图1 滑坡工程地质平面图

1.2 构造及地层岩性

该滑坡处于扬子准地台的次级构造单元摩天岭台隆区范围内,毗邻北东—南西走向的姚渡断裂及碧口—太平川复背斜。基岩的顺层逆断层较发育,可见张性裂隙、剪切裂隙以及不同走向的缓倾角裂隙。基岩岩性主要为长城系碧口群的灰白色薄层状绢英千枚岩与变质凝灰岩,产状为NW274°～NE71°/SW69°～SE77°。岩层走向与河流近于平行且有倾向河流的缓倾角裂隙存在。覆盖物以第四系坡积碎石土及冲积砂卵砾石为主。现今库区基本已达到冲淤平衡,在滑坡体前缘形成了60 m～70 m厚的水库淤积泥沙。

1.3 水文地质条件

滑坡区地下水较为丰富,地下水位较高。第四系孔隙水主要赋存于坡表覆盖层中,基岩裂隙水主要赋存于绢英千枚岩的裂隙中。坡体以大气降水补给为主,通过两种途径排泄:一是直接在岸坡前缘排入白龙江,二是先汇入地表冲沟再以地表径流的形式顺沟流入白龙江。根据钻孔资料,一般地下水埋深为15 m～20 m,个别为40 m。除冲沟中有常年流水外,在斜坡的前缘和中部多处出现沼泽地,泉水出露也很常见。

1.4 滑坡形成机理

该滑坡为一典型的陡倾顺层岩质斜坡。滑床基岩陡倾坡外,倾向为SW,倾角约 70°,而上部倾倒体倾向SE,倾角20°～60°。在河谷的下切发育过程中斜坡岩体向临空面卸荷回弹,坡体内应力调整。然后岩体向临空面发生初始倾倒变形,坡表沿着岩层层面出现较多的张裂缝。斜坡变形不断地发展,坡脚附近岩体向临空面的倾倒变形加剧,层状岩体沿层理面发生滑移,并开始从坡脚自下至上作悬臂梁弯曲。其后又因下部受阻而发生弯曲折断,形成倾倒体。当各层最大弯曲、弯折带部位相互贯通、并形成倾向坡外的断续的拉裂面时,坡体将沿该折断面发生蠕滑变形,最终形成蠕滑—拉裂型滑坡。其演化阶段可分为斜坡岩体内应力调整、斜坡岩体初始变形、斜坡岩体初始滑移—倾倒变形、斜坡岩体破坏四个阶段[21]。

2 滑坡体渗流分析

2.1 模型的建立及天然渗流场的模拟

根据滑坡最具代表性的Ⅱ-Ⅱ工程地质剖面图(见图2),建立渗流计算模型示意图如图3所示,右边界截取至河床中心,左边界截取至坡顶上部,即取水平方向和垂直方向上的长度分别为1550 m和980 m。计算模型的边界条件:选取底面以及左右两侧为不透水边界;坡表底部至库水位之间为蓄水高度随时间变化的变水头边界,蓄水位以上至模型顶部为降水边界。

图2 滑坡Ⅱ-Ⅱ剖面工程地质剖面

图3 渗透计算模型示意

在边坡渗流计算中涉及到饱和渗流和非饱和渗流的共同作用,在饱和区介质渗透系数为常数,而在非饱和区介质的渗透系数与非饱和部分介质的基质吸力和含水率都密切相关。根据已有资料、模拟反分析以及工程经验等综合手段确定基岩饱和渗透系数为6.5×10-8m/s,倾倒体和滑体为1.6×10-6和3.0×10-6m/s、前缘冲积砂卵砾石为 6.0×10-6m/s。模拟过程中使用的土-水特征曲线及渗透函数曲线通过已有文献资料,采用类比法确定[22-23]。

降雨入渗导致坡体土中基质吸力的丧失会对坡体稳定性造成重要的影响。根据当地气象站的统计资料,近坝地段的年降雨量为854.8mm,因此在滑坡体表面的降雨边界上施加此降雨强度,把年降雨量均匀分配。

在对库水位升降条件下的渗流场进行模拟时,需首先确定坡体内的初始地下水位,它是边坡渗流场模拟的基础。初始地下水位的获得通常有三种方法:一是根据钻孔中地下水位的埋深资料,利用插值方法或趋势面分析得到;二是先利用类比方法确定该地区的水力坡度,利用该水力坡度和现今的库水位推算出各单元的地下水位埋深;三是对模型进行稳定流模拟,利用模拟结果作为平稳阶段的地下水位[6]。本次模拟采用了后两种方法,首先利用水力坡度和稳定水位(628.4 m)推算出各单元地下水位埋深,利用该埋深作为初始水头赋给计算模型的各个单元,进行稳定流模拟,然后以此为基础用瞬态法(非稳定流)模拟库岸边坡内的地下水位随库水位的变化。

2.2 库水位上升和下降过程中渗流场模拟

库水位动态调控与水库的出入库流量直接相关。由于河床呈“v”字形形态,水位上升和下降时库容不断变化。蓄水初期的库容较小,水位上升较快;达到高水位时,库容增大使水位上升变慢。库水位下降过程中的水位变动规律与上升过程恰好相反。库水位升降这一特点使其调控曲线非常接近正弦半波曲线。因此,以正弦半波曲线表示库水位升降值与调控时间的关系[24]:

水位上升:

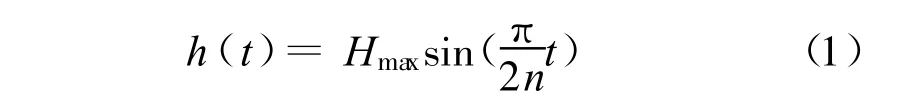
水位下降:

式中:h(t)为库水位升降值;n为库水位调控设计上升(下降)到最高(最低)点的天数;Hmax为最大上升或下降高度;t为水位上升(下降)的时间。

该水库从1975年底开始蓄水,库水位从628.4 m上升到704.0 m的正常蓄水位;水库在汛期运行时,需将水库水位降低到694.0 m,以便洪水到来时拦蓄洪水,洪峰过后库水位又迅速降低。因此,水库运行后,水位将在694.0 m～704.0 m之间变动,库水位骤降的情况是存在的。结合水库调度时可能采用的水位升降速率控制范围,考虑0.5 m/d、1.0 m/d、2.0 m/d三种库水位变化速率,按照式(1)、式(2)的正弦半波曲线模型对库水位升降阶段不同时刻的坡体内的渗流场进行模拟。

2.2.1 库水位上升过程中渗流场模拟

图4表明,随着库水位升高,滑坡渗流场的改变主要集中在滑坡体前缘,影响深度较为有限;而深部基岩渗透系数较小,故其水位线变动较小。滑坡体前缘随着库水位升高,含水率呈现逐渐增加的趋势;随着时间的推移,其饱和程度越来越大,最终部分区域达到完全饱和。

图4 库水位以不同的速率由628.4 m上升至704 m滑坡地下水位线特征(前缘局部)

从水位线的形态可以看出,在滑坡体前缘地下水位线都呈现出下凹的形态,水位变动速率越大这种形态就越明显。这是因为水位快速上升阶段,水由水库向坡体内渗透需要一个过程,距离水库越远的坡体其渗透所需要的时间就越长,因而出现地下水位线右高左低的情况。如果水位缓慢上升则应该出现平缓的变动。

2.2.2 库水位下降过程中渗流场模拟

图5表明,水位消落过程中滑坡渗流场的改变也主要集中在滑坡前缘,且影响深度较为有限。库水位以不同速率消落,滑动体前缘地下水位线都呈现出向上凸的形态,正好和库水位上升时的水位线形态相反,且库水位消落速率越快,水位线上凸越明显。当库水位以2.0 m/d的速率骤降时,滑坡体前缘较深部的地下水位甚至都来不及改变,出现几乎竖直的水位线。同时,滑动体前缘水位线的变化明显滞后于库水位下降幅度,滑坡体内地下水流速矢量指向坡外。

图5 库水位以不同的速率由704m下降至694 m滑坡地下水位线特征(前缘局部)

3 库水位升降期间滑坡稳定性

将使用有限元法计算出的各个水位下的坡体渗流场与基于极限平衡的稳定性计算方法(Ordinary、Bishop、Janbu、M-P)耦合 ,计算出Ⅱ-Ⅱ剖面和Ⅱ-2剖面在库水位升降过程中的稳定性。为了简单起见,不再列出各次稳定性计算的详细结果,只将其汇总成图。

3.1 库水位上升时滑坡的稳定性

由图6、图7可知,在水位上升过程中滑坡稳定性总体为先降低再升高,两剖面的稳定性系数均在以0.5 m/d的速率上升时在约650 m的水位时降到最低,Ⅱ-Ⅱ剖面和Ⅱ-2剖面的稳定性系数较628.4 m的初始水位时分别降低了0.0043、0.0103。然后它们的稳定性系数又迅速增高,两者均以2.0 m/d的速率上升时在约700.0 m的水位时达到最大值,前者较原河水位状态增高了0.0215,后者增高了0.0525。水位继续上升到704.0 m的正常蓄水位时稳定性又有所降低。

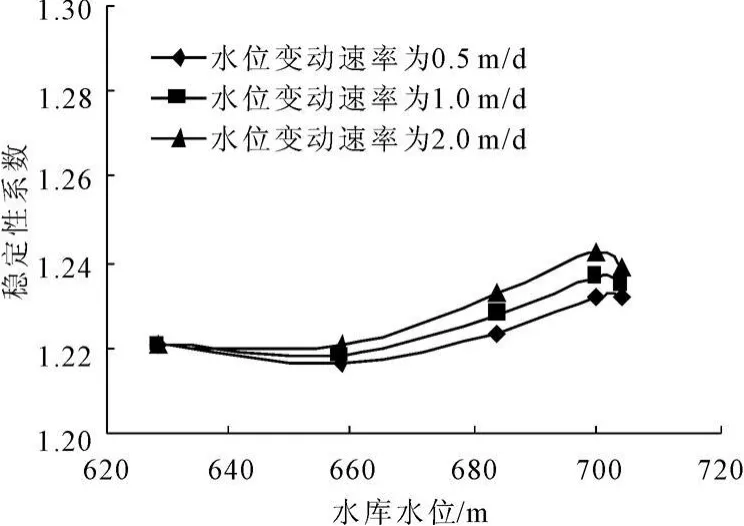
图6 Ⅱ-Ⅱ剖面在以不同上升速率上升过程中滑坡的稳定性变化

图7 Ⅱ-2剖面在以不同上升速率上升过程中滑坡的稳定性变化

库水位在快速上升过程中,滑坡体内地下水位的变化总是要滞后于库水位的变化。库水不断渗入滑坡体内,水的重力荷载也会增大,产生对滑坡体向内的推力。在库水位从628.4 m的原河水位上升到约650 m的过程中,前缘因滑坡体的渗透性较大而水渗入较多,加之本来该滑坡地下水位就较高,水入渗前缘滑带造成的岩土体物理力学参数的降低对滑坡的影响超过了水位上升过程中水的重力荷载对滑坡稳定性的贡献,因而这段时间内滑坡的稳定性降低。同时可以看出,库水位上升速率越慢对滑坡的稳定性越不利,Ⅱ-2区滑动体因有一半会受到水位波动的影响,稳定性降低得较多。

当库水位上升超过约650 m后,滑坡体的稳定性系数迅速增大。Ⅱ-Ⅱ剖面代表的整块坡体本身体积较大,骤升过程中水并没有渗入滑坡体深部对岩土体造成软化等不良作用,水位的变化影响范围仅为坡体浅表部分,对滑坡稳定性增大的主要原因是水的重力荷载作用。Ⅱ-2区滑动体体积较小,虽然骤升过程中水渗入弱化滑带土的性质,但水的重力荷载对其影响更为显著,稳定性系数增大也更多。

3.2 库水位消落时滑坡的稳定性

3.2.1 水库淤积前

由图8、图9可知,在水库淤积前水位骤降过程中稳定性总体降低。库水位突然降低时滑坡体内地下水水位下降较滞后,较大的水力梯度形成较大的动水压力,加大了沿渗流方向的滑动力。水位降低速率越快,稳定性降低越多。Ⅱ-Ⅱ剖面以0.5 m/d、1.0 m/d、2.0 m/d降低时稳定性系数分别降低0.0115、0.0123、0.0155,而 Ⅱ -2 剖面为 0.0333、0.0348、0.0435。前者只在前缘局部受到库水位快速消落的影响,重力荷载的变化是主导因素,因而基本上呈直线趋势下降;后者对水位消落时坡体内动、静水压力的不断变化更敏感,稳定性在约700.0 m有突然降低现象后又趋于平稳。水位的骤降对Ⅱ-2区滑坡体的稳定性有很大的影响,如果在水位骤降的同时出现暴雨或者地震等不利的工况,该区将有可能失稳。

图8 水库淤积前Ⅱ-Ⅱ剖面在以不同下降速率下降过程中滑坡的稳定性变化

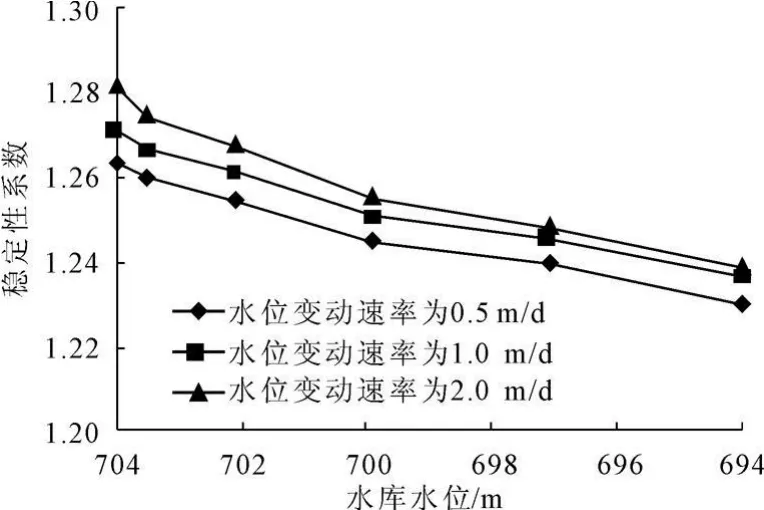
图9 水库淤积前Ⅱ-2剖面在以不同下降速率下降过程中滑坡的稳定性变化

3.2.2 水库淤积后

由图10、图11可知,在水库达到冲淤平衡后水位骤降过程中稳定性降低趋势和淤积前相似。Ⅱ-Ⅱ剖面以0.5 m/d、1.0 m/d、2.0 m/d降低时稳定性系数分别降低0.0090、0.0095、0.0133,而Ⅱ -2剖面为0.0228、0.0240、0.0323。水库淤积后水位的骤降水对滑坡体的稳定性依然有很大的影响,但水库淤积泥砂覆于滑坡体前缘,对滑坡体起到“压脚”的作用,增加了滑坡的稳定性,从而降低了失稳的可能。

图10 水库淤积后Ⅱ-Ⅱ剖面以不同下降速率下降过程中滑坡的稳定性变化

图11 水库淤积后Ⅱ-2剖面以不同下降速率下降过程中滑坡的稳定性变化

4 结 论

本文运用非饱和渗流理论对某库岸滑坡在水库运行时的渗流场和相应库水位时的稳定性进行了计算分析,得到以下认识和结论:

(1)该滑坡在水库蓄水时,水位在约650 m之前稳定性降低,然后再上升;在过了约700 m后稳定性又有所下降。库水位上升速率越大,地下水位变化越具有明显的滞后特点。

(2)在库水位消落过程中,虽然渗流场的改变主要集中在滑坡前缘,且影响深度较为有限,但稳定性却明显降低。不同消落速度造成滑坡稳定系数降低程度不同,但地下水位均滞后于库水位的下降,滑坡体内地下水流速矢量指向坡外。水位消落速度越快,地下水位线也越陡。

(3)对于该滑坡,在库水位消落过程中,水位在700 m左右时滑坡的稳定性较低。并且在同一特征水位下,库水位上升时的稳定性系数比下降时的稳定性系数大。因此在库水位降到700 m时是水库调度时的危险水位,应减慢水位消落的速度。

(4)水库淤积后水库运行过程中稳定性变化趋势总体与淤积前相似,但淤积泥沙对滑坡体起到“压脚”的作用,增加了滑坡的稳定性,降低了失稳的可能。

[1]朱冬林,任光明,聂德新,等.库水位变化下对水库滑坡稳定性影响的预测[J].水文地质工程地质,2002,29(3):6-9.

[2]林仕祥,张奇华,黄振伟.三峡水库蓄水运行对猴子石滑坡稳定性影响分析[J].资源环境与工程,2009,23(S2):95-99.

[3]刘才华,陈从新,冯夏庭.库水位上升诱发边坡失稳机理研究[J].岩土力学,2005,26(5):769-773.

[4]黄波林,许模.三峡水库水位上升对香溪河流域典型滑坡的影响分析[J].防灾减灾工程学报,2006,26(3):290-295.

[5]王德咏,李科.库水位上升对千将坪滑坡的影响研究[J].灾害与防治工程,2007,(2):15-19.

[6]刘红岩,秦四清.库水位上升条件下边坡渗流场模拟[J].工程地质学报,2007,15(6):799-801.

[7]Desai C S.Drawdown analysis of slopes by numerical methods[J].Journal of Geotechnical Engineering,ASCE,1977,103(7):667-676.

[8]Mehmet M.Berilgen.Investigationof stability of slopes under drawdown conditions[J].Computers andGeotechnics.2007,34:81-91.

[9]时卫民,郑颖人.库水位下降情况下滑坡的稳定性分析[J].水利学报,2004,(3):76-80.

[10]唐辉明,章广成.库水位下降条件下斜坡稳定性研究[J].岩土力学,2005,26(S2):11-15.

[11]廖红建,盛 谦,高石夯,等.库水位下降对滑坡体稳定性的影响[J].岩石力学与工程学报,2005,24(19):3454-3458.

[12]刘新喜,夏元友,练操,等.库水位骤降时的滑坡稳定性评价方法研究[J].岩土力学,2005,26(9):1427-1431.

[13]Qun Chen,Limin Zhang,M.ASCE.Stability of a gravel soil slope under reservoir water level fluctuations[A].Proc.ASCE Geo-Frontiers[C]//Austin,Texas,Jan.ASCE Geotechnical Special Publication No.140,M.Gabr,J.J.Bowders,D.Elton,and J.G.Zomberg,eds.,2005:2951-2960.

[14]丁秀丽,付敬,张奇华.三峡水库水位涨落条件下奉节南桥头滑坡稳定性分析[J].岩石力学与工程学报,2004,23(17):2913-2919.

[15]莫伟伟,徐平,丁秀丽.库水位涨落对滑坡稳定性影响研究进展[J].地下空间与工程学报,2006,2(6):997-1002.

[16]胡新丽,David M.Potts,Lidija Zdravkovic,等.三峡水库运行条件下金乐滑坡稳定性评价[J].地球科学(中国地质大学学报),2007,32(3):403-408.

[17]罗红明,唐辉明,章广成,等.库水位涨落对库岸滑坡稳定性的影响[J].地球科学(中国地质大学学报),2008,33(5):687-692.

[18]Fredlund D G,Rahardjo H.非饱和土力学[M].陈仲颐(译).北京:中国建筑工业出版社,1997.

[19]Griffiths DV,Lane PA.Slope stability analysis by finite elements[J].Geotechnique,1999;49(3):387-403.

[20]Lane PA,Griffiths DV.Assessment of stability of slopes under drawdown conditions[J].Geotech Geoenviron Eng,2000,126(5):443-450.

[21]任光明,夏 敏,李 果,等.陡倾顺层岩质斜坡倾倒变形破坏特征研究[J].岩石力学与工程学报,2009,28(S1):3193-3200.

[22]Fredlund D G,Xing Anqing.Equations for the soil-water characteristic curve[J].Canadian Geotechnical Journal,1994,31(3):521-532.

[23]Fredlund D G,Xing Anqing,Huang Shangyan.Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J].Canadian Geotechnical Journal,1994,31(3):533-546.

[24]李 晓,张年学,廖秋林,等.库水位涨落与降雨联合作用下滑坡地下水动力场分析[J].岩石力学与工程学报,2004,23(21):3714-3720.