水工全级配与湿筛混凝土强度关系的研究
2011-06-05韩巍巍
郑 丹,韩巍巍,张 寅
(1.重庆交通大学河海学院,重庆 400074;2.北京中交水运规划设计院有限公司,北京 100007)
1 研究背景
水工混凝土通常采用最大骨料粒径为80mm或150mm的三、四级配混凝土,由于全级配混凝土试件尺寸大,试验工作量大、难度高。因此常采用湿筛法剔除拌合物中超过40mm的大骨料,成型150mm大小的试件进行强度试验,并以此结果进行大坝的设计和安全评价[1]。由于全级配和湿筛混凝土实际配合比并不相同,两者的力学特性差异较大,能否用湿筛后小试件的强度试验结果来推测大坝全级配混凝土的强度,一直是工程界和学术界所普遍关心的问题。国内外有关研究人员进行了大量的试验研究,并取得了一定的研究成果[2-4],但由于试验条件的差异且各自的试验数据有限,二者强度之间的关系问题仍然未得到较好的解决。因此,有必要研究全级配与湿筛混凝土强度差异的物理机理,更为准确地分析大坝混凝土的强度,为高坝等大型混凝土结构设计和安全性评价提供参考。
2 现有研究成果回顾
2.1 试验结果
由于近年来研究人员开展了大量的全级配混凝土试验[2,5-6],本文统计了现有文献中的试验结果,得出了四级配、三级配和湿筛混凝土的强度关系,如图1和图2所示。

图1 四级配混凝土与湿筛小试件强度比值
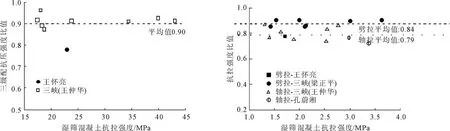
图2 三级配混凝土与湿筛小试件强度比值
从图1和图2可以看出,随着最大骨料粒径的增加,混凝土强度随之降低,四级配和三级配混凝土强度均小于湿筛混凝土的强度;同时可以看出轴拉强度降低最大,劈拉强度次之,抗压强度降低最小。
2.2 理论分析
固体的强度随试件尺寸增加而减小,这被称之为“尺寸效应(Size effect)”。现有混凝土强度尺寸效应的模型主要有以下3种。
(1)Weibull统计理论[7]。Weibull假设:①材料的某一个单元达到强度极限时,结构就失效;②每个单元的失效是独立的;③材料的极限强度是随机的,并在此基础上采用统计方法导出了混凝土的尺寸效应律:

式中:σN为混凝土的强度;D为试件尺寸,k0为常数。
(2)基于能量释放理论的Bazant尺寸律[8]。由于Weibull统计理论忽略了由于宏观裂纹发展而引起的结构能量释放的影响,因此不能很好地反应混凝土等准脆性材料的尺寸效应。Bazant从预制裂纹梁的断裂试验结果出发,认为混凝土的裂纹尖端存在着一定长度的断裂过程区,在发生破坏的过程中,断裂过程区中的微裂纹也会消耗能量,并采用能量理论导出了尺寸效应律:
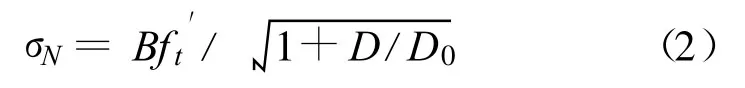
式中:σN为混凝土的强度为无尺寸效应的混凝土抗拉强度;D为宏观裂缝的尺寸;B和D0为与尺寸无关的常数,可以认为D0为断裂过程区的长度。
(3)基于分形的Carpinteri尺寸律[9]。Carpinteri等认为混凝土的尺寸效应主要是由裂纹表面的侵入式分形特性理论(即表面粗糙度的分形属性)和间隙分形特性理论(代表着微裂纹的分形分布)所引起的,因此其尺寸律可以表示为:
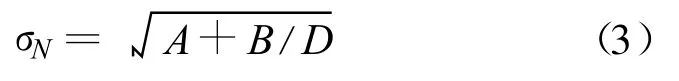
式中:σN为混凝土的强度;D表示试件的尺寸;A和B为常数,可由试验数据拟合得到。
从现有研究成果来看,混凝土材料尺寸效应产生的根本原因是裂纹附近产生了应力集中,使得裂纹前沿的微裂纹发生开裂,从而在裂纹尖端形成非奇异的应力分布,使得线弹性断裂力学不能直接应用于混凝土的断裂分析[10],在宏观上即表现为测量得到的混凝土强度具有尺寸效应。由于Weibull的尺寸律假设单元破坏及对应于材料破坏,因此更适用于完全脆性材料;Bazant的尺寸律是从混凝土非线性断裂过程出发,物理意义清楚,与具有初始预置裂纹长度的三点弯曲或四点弯曲梁试验结果吻合较好,但与无预置裂纹的拉压试验结果相比误差较大,需进行修正;Carpinteri尺寸律和试验结果吻合较好,但由于分形理论发展时间较短,其中的很多参数物理意义并不明确,较难应用推广。
由于现有尺寸律并未考虑混凝土骨料级配的影响,不能直接应用于分析全级配与湿筛混凝土强度比值,研究人员采用其它方法针对这一问题开展了研究。李嘉进[11]采用统计分析的方法,研究了骨料粒径、级配和试件尺寸对混凝土强度的影响规律。宋玉普[12]通过内时损伤模型建立了全级配和湿筛混凝土的本构关系,分析了二者之间力学特性的差异。虽然已经进行了很多全级配混凝土的试验和理论研究,但全级配和湿筛混凝土的力学特性尤其是强度差异的物理机理并不清楚。现有研究多数是对试验结果的简单拟合,从而得出强度比值的经验公式,缺乏理论依据。因此,本文从混凝土的细观破坏机理出发,分析了全级配和湿筛混凝土强度的关系。
3 理论模型
从细观机理分析,混凝土的破坏由微裂纹的产生、扩展以及串接最后形成宏观裂纹而引起的[13]。因此,从断裂力学的角度分析,混凝土强度大小主要由骨料和砂浆界面的强度以及混凝土破坏时控制性裂纹的大小决定的。对于全级配混凝土和湿筛混凝土而言,由于拌合物性能基本一致,因此可以认为全级配混凝土与湿筛混凝土强度的差异主要体现在发生破坏时控制性裂纹的大小不同。对于预制裂纹长度的三点弯曲或四点弯曲混凝土试件而言,其控制性裂纹长度即为预置裂纹长度;而对于混凝土的抗拉抗压破坏试验,其控制性裂纹长度与其混凝土内微裂纹分布情况和破坏模式有关。
本文通过分析混凝土在轴拉、劈拉以及抗压破坏下的裂纹扩展过程,得到了混凝土破坏时控制性裂纹的大小,并在一定简化的基础上,通过对Bazant的断裂力学尺寸律的修正来分析全级配和湿筛强度之间的关系。
3.1 抗拉强度
混凝土受拉破坏时裂纹扩展过程如图3所示[14-15]。当混凝土未承受荷载时,内部微裂纹主要分布在骨料和砂浆的界面上;当混凝土承受拉伸荷载时,界面上的裂纹首先扩展,然后被具有更高强度的水泥砂浆所束缚而停止扩展。当外加荷载继续增加,裂纹发生失稳扩展,混凝土材料发生破坏。
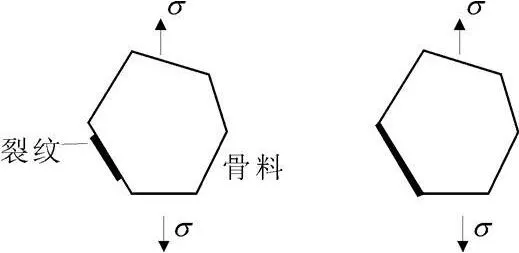
图3 混凝土受拉破坏裂纹扩展过程
由于混凝土在承受轴向拉伸荷载时,其内部应力分布基本均匀,同时骨料与水泥基体间界面强度最低,是材料中最弱的一环,由以上分析可以认为混凝土破坏时的控制性币状裂纹存在于骨料与基体界面上,其大小与混凝土的最大骨料粒径相等。由于全级配混凝土的最大骨料粒径远远大于湿筛混凝土,这就使得全级配混凝土的强度低于湿筛混凝土的强度。根据Bazant的尺寸效应律(式2),全级配和湿筛混凝土轴拉强度的比值可以表示为:
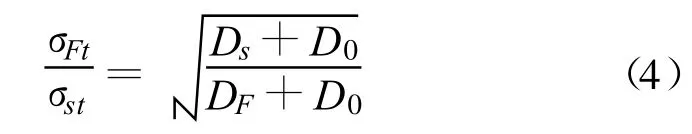
式中:σFt和σst分别为全级配和湿筛混凝土的轴拉强度;DF和Ds分别为全级配和湿筛混凝土的最大骨料粒径;D0表示混凝土断裂过程区的长度。
3.2 劈拉强度
混凝土劈拉强度试验装置及试件的应力分布如图4所示。由图4可知,在混凝土劈拉试验中,拉应力区主要集中在轴线附近,试件在此区域(如图4阴影所示)发生劈拉破坏。虽然混凝土的劈拉破坏与直轴拉破坏形式类似,但由于其破坏面固定于一定区域,因此其发生破坏的裂纹并不一定位于最大粒径骨料的界面上。
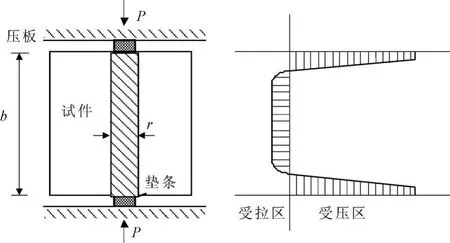
图4 混凝土试验装置及试件应力分布
本节从统计学的角度出发,计算分析混凝土在劈拉破坏下控制性裂纹的平均期望值。如图4所示,混凝土劈拉试验试件尺寸为b×b×l,假设混凝土劈拉破坏时拉应力区厚度为r,则拉应力区的体积为Vs=rbl,混凝土试件的总体积为 V=b2l。可认为混凝土中裂纹长度分布满足Weibull统计律,因此混凝土劈拉破坏时,混凝土和拉伸断裂区内最大裂纹尺寸的关系可表示为:
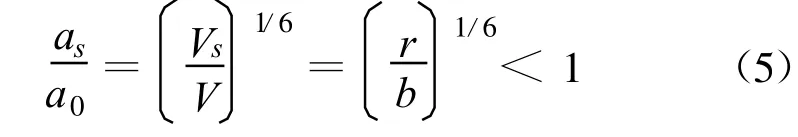
式中:as为拉伸断裂区内最大裂纹尺寸;a0为混凝土内最大裂纹尺寸。
由前面分析可知,混凝土受拉破坏时内最大裂纹尺寸a0即为骨料粒径D。因此,混凝土劈拉破坏时,其控制性裂纹的平均期望值为D(r/b)1/6。根据Bazant的尺寸效应律,全级配和湿筛混凝土劈拉强度的比值可以表示为:
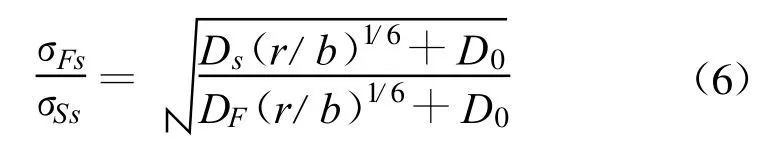
式中:σFs和σSs分别为全级配和湿筛混凝土的轴拉强度。
由式(6)可知,全级配和湿筛混凝土的劈拉强度比值可表示为:
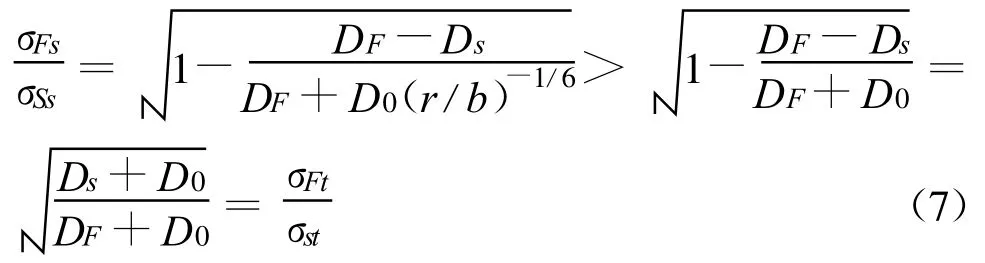
由式(7)可以看出,发生劈拉破坏时,混凝土内的控制性裂纹长度比轴拉破坏时小,因此全级配湿筛混凝土劈拉强度的比值要大于二者的轴拉强度比值。
3.3 抗压强度
混凝土受压破坏时裂纹扩展过程如图5所示[14-15]。当混凝土受轴向压缩荷载时,随着外荷载的逐渐增大,初始裂纹发生开裂并扩展至整个界面,然后被具有更高强度的水泥砂浆所束缚,如图5(b)所示;当外加荷载继续增加,裂纹会发生弯折扩展,扩展后的翼型裂纹沿着曲线的方式继续扩展,最终扩展至与外加压应力平行的方向,如图5(c)所示;由于弯折裂纹的扩展方向和外荷载方向平行,裂纹可以稳定扩展直至与相邻的微裂纹发生串接导致破坏[14]。
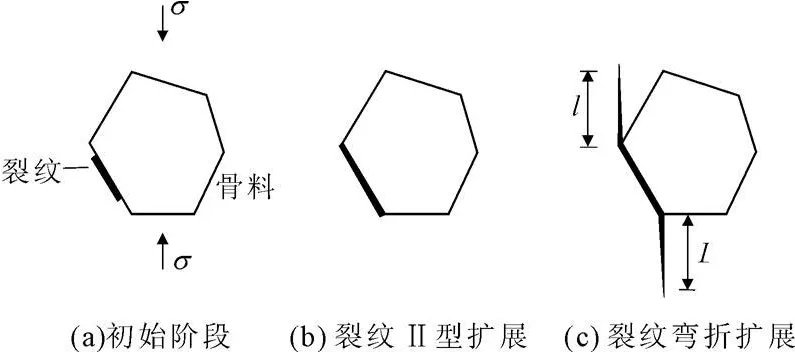
图5 混凝土受压破坏裂纹扩展过程
可以近似地用周期性分布裂纹模型来描述混凝土在受压破坏时的行为,如图6所示。图6中F为等效劈拉力,2w为裂纹间距,l为弯折裂纹的扩展长度。其中等效劈拉力F可以表示为:
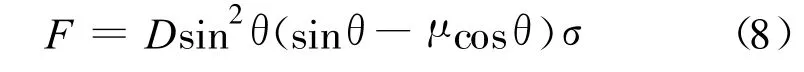
式中:σ为轴向压应力;D为初始裂纹长度;θ为裂纹与轴向荷载夹角;μ为断裂面的摩擦系数。
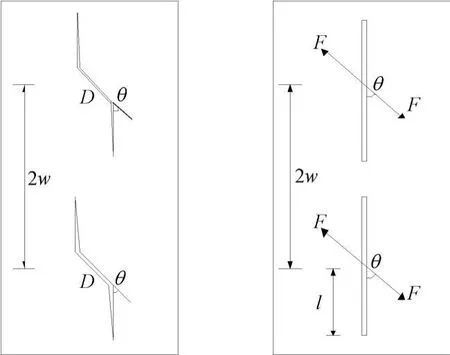
图6 混凝土单向压缩等效裂纹模型
因此,在如图6所示的周期性裂纹模型下,由应力强度因子表示的破坏控制方程为[14]:
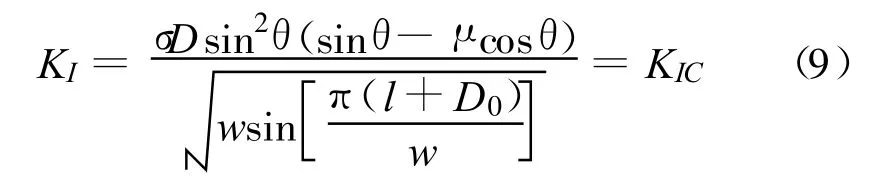
式中:KI为裂纹应力强度因子;KIC为临界应力强度因子(断裂韧度)。
由图6和式(9)可以看出,随着外荷载σ的逐渐增大,裂纹逐渐扩展,弯折裂纹长度 l也逐渐增加,当增加到(l+D0)/w=1/2时,图6中的裂纹等效应力强度因子达到极值,材料不能承受更高的荷载,混凝土发生破坏。因此根据式(9),可把全级配和湿筛混凝土抗压强度的关系表示为:

式中:w(D)表示直径为D的骨料间距。
由式(10)可知,混凝土受压破坏时的强度不仅与控制型裂纹尺寸(最大骨料粒径D)有关,同时也和骨料间距w有关;骨料间距越大,混凝土材料的强度越高。水工混凝土中骨料粒径的概率密度分布函数一般可以表示成:

式中:ρ(D)表示直径为D的骨料概率密度分布,k=Dmax/Dmin,Dmin和Dmax分别为混凝土中的最小和最大骨料直径,n=3和n=2.5分别表示等体积和Fuller级配。可以假设混凝土内骨料均匀分布。
因此由式(11)可得到骨料的间距和粒径满足以下关系:
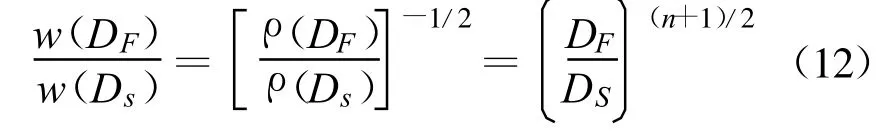
将式(12)代入式(10),可得到全级配和湿筛混凝土抗压强度的比值:
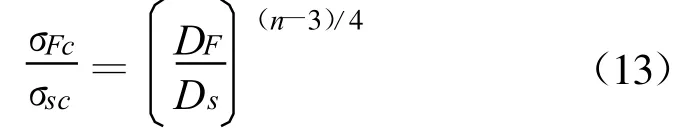
式中:σFc和σsc分别为全级配和湿筛混凝土的抗压强度。
4 模型与试验验证
根据上节提出的模型,可以求出全级配与湿筛混凝土的轴拉、劈拉强度和抗压强度比值与最大骨料粒径的关系,如图7所示。在本文计算中各参数取值如下:四级配混凝土最大骨料粒径为150mm,三级配混凝土最大骨料粒径为80mm,湿筛混凝土最大骨料粒径为40mm。断裂过程区尺寸D0为20mm,劈拉破坏下的断裂区宽度r/b=0.1,骨料粒径概率密度分布函数满足fuller分布(n=2.5)。
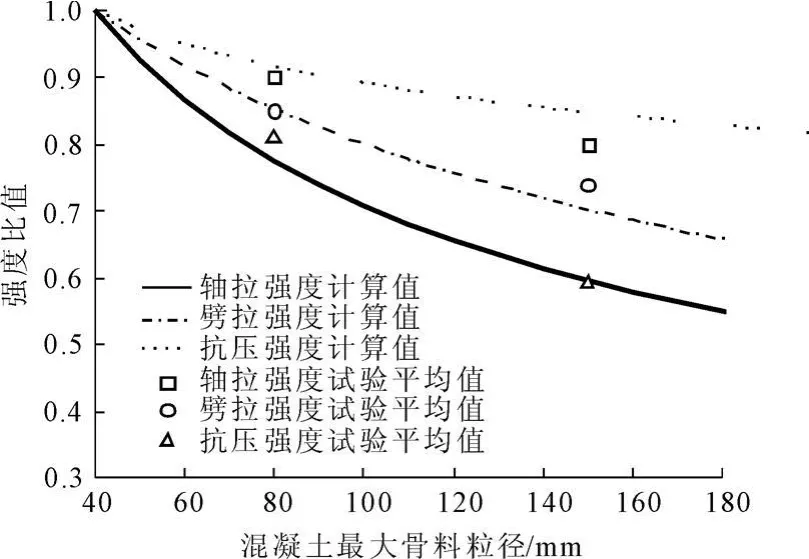
图7 不同最大骨料粒径的混凝土与湿筛混凝土的强度比值
由图7可以看出,本文提出的模型与试验吻合较好,说明本文提出的模型能较好地解释全级配混凝土与湿筛混凝土强度的关系。随着最大骨料粒径的增加,混凝土内控制性裂纹尺寸增大,因此强度也随之降低,因此四级配和三级配混凝土的强度小于湿筛混凝土的强度;同时可以看出对于不同骨料粒径的混凝土而言,全级配和湿筛混凝土的轴拉强度的比值最小,劈拉强度次之,抗压强度最大。
需要指出的是,本文在推导全级配和湿筛混凝土抗压强度比值的理论模型时,对混凝土的抗压破坏过程进行了简化,忽略了非控制性裂纹的影响,但实际上混凝土破坏时微裂纹的初始分布和扩展演化也会对强度产生影响,这也会给模型中全级配和湿筛混凝土抗压强度比值计算结果带来误差,造成与试验结果有一定差距。同时,由于粉煤灰掺量、掺气量和浇筑振捣方式等都会对混凝土内裂纹密度和间距产生较大影响,因此也有部分试验中出现混凝土全级配大试件和湿筛小试件的抗压强度相当的情况[2]。
5 结 论
由于混凝土材料是由骨料、砂浆、孔隙及界面过程区组成的不均质材料,其破坏是由微裂纹扩展、串接最后形成宏观裂纹的复杂过程,因此混凝土等准脆性材料的强度问题一直是世界级的难题。本文着重分析了影响全级配和湿筛混凝土强度最主要的因素,通过研究抗拉、劈拉和抗压强度试验中混凝土的细观破坏机理,确定了各种破坏形式下混凝土内控制裂纹的长度,并在Bazant断裂力学尺寸律和一定的理论假设基础上,建立了全级配和湿筛混凝土的尺寸效应模型,分析了二者强度之间的关系。
从本文的研究中可以得出:水工混凝土强度主要由骨料和砂浆界面的断裂韧度以及控制性裂纹的长度确定,全级配与湿筛混凝土强度的差异主要是因为发生破坏时控制性裂纹大小不同。同时,全级配和湿筛混凝土强度比值以轴拉最小,劈拉次之,轴压最大。这是由于混凝土受直接拉伸荷载时,控制性裂纹大小与最大骨料粒径相同;而在劈拉破坏时,混凝土的破坏发生在劈拉力轴线附近的拉应力区,因此控制性裂纹尺寸较小;混凝土受压破坏时存在裂纹稳定扩展的过程,因此控制性裂纹的大小不仅仅与骨料粒径有关,同时也和骨料间距有关。
[1]DL/T5150-2001.水工混凝土试验规程[S].北京:水利电力出版社,2001.
[2]邓宗才著.高性能大坝混凝土的强度和变形[M].北京:科学出版社.2006:52-54.
[3]杨成球,吴政.全级配混凝土基本力学特性试验研究[J].水利水电科技进展,2000,20(3):29-32.
[4]李光伟,杨代六.拱坝大体积混凝土力学特性的试验研究[J].水电站设计,2006,22(2):88-92.
[5]邓宗才,李庆斌,傅华.人工骨料全级配大坝混凝土的拉压力学性能[J].水利学报,2005,36(2):214-224.
[6]王怀亮.复杂应力状态下大骨料混凝土力学特性的试验研究和分析[D].大连:大连理工大学,2007.
[7]WeibullW.A statistical distribution function of wide applicability[J].J.Appl.Mech,1951,18(3):293-297.
[8]Bazant ZP.Scaling laws in mechanics of failure[J].J Engng Mech,1993,119(9):1828-1844.
[9]Carpinteri A,Chiaia B,Ferro G.A new explanation for size effects on the flexural strength of concrete[J].Magazine of Concrete Research,1997,49:45-53.
[10]Saouma V,Natekar D,Hansen E.Cohesive stresses and size effects in elasto-plastic and quasi-brittle materials[J].International Journal of Fracture,2003,119(3):287-298.
[11]李嘉进.试件尺寸和骨料粒径对混凝土强度的影响[J].水电站设计,1991,7(3):20-27.
[12]宋玉普,王怀亮.全级配大体积混凝土的内时损伤本构模型[J].水利学报,2006,37(7):769-777.
[13]Neville A.Properties of concrete[M].Pitman London,1973:570-572.
[14]Horii H,Nemat-Nasser S.Brittle Failure in Compression:Splitting,Faulting and Brittle-Ductile Transition[J].Philosophical Transactions for the Royal Society of London,1986,319:337-374.
[15]Ashby M,Hallam S.The failure of brittle solids containing small cracks under compressive stress rate[J].Acta Metall,1986,34:497-510.
