模糊数学存在的问题及解决方法
2011-06-05刘开第庞彦军周少玲
刘开第,庞彦军,周少玲
(河北工程大学不确定信息研究所,河北邯郸 056038)
上世纪60年代,随着模糊集合的出现,开启了对非随机不确定性的研究时代。模糊性是一种以“边界不清”为特征的非随机不确定性,模糊数学是描述和处理模糊性的理论与方法。
解决任何一种不确定性问题,都要在“不确定性定量表征”基础上实现“不确定性转换”。并且只有“定量表征”是合理的、符合实际的,不确定性转换才可能是正确的、有用的。因为只有实现不确定性转换才能解决要解决的不确定性问题,所以,“不确定性转换”是不确定性研究中最具实质性的内容。
在研究随机性时,“不确定性定量表征”和“不确定性转换”并没有引起人们的太多关注,因为在概率方法的公里体系下,“不确定性定量表征”就是假定当前随机性服从哪一种“已知分布”,而“不确定性转换”则归结为确定已知分布的“联合分布”。但是,对非随机不确定性则不然,它不具有随机性要求的“理想化”条件,因而没有公理化体系支撑;对于不同类型的不确定性要选择不同的“定量表征”方法,特别是,具有不同内涵的“不确定性转换”,对应不同的实现转换的计算方法。
实现“不确定性转换”要解决两个问题,一是揭示不确定性转换的非线性转换机理,二是给出实现不确定性转换基于机理的非线性计算方法。
对于非随机不确定性的研究虽然进行了数十年,但是鲜见从理论上研究“不确定性转换”为什么是非线性转换而不是线性转换的原因,由于对不确定性转换的非线性转换机理普遍缺乏足够认识,所以很难构建正确实现不确定性转换的非线性计算方法,使得像模糊数学、层次分析法等一些重要的非随机不确定性理论与方法,都把不确定性转换的非线性转换机理和实现不确定性转换的非线性计算方法作为遗留问题留了下来。
模糊数学用模糊集合描述模糊信息,用论域U上模糊集合到论域V上模糊集合转换来处理U上模糊信息。所以模糊集合转换是模糊数学中的“不确定性转换”。
模糊数学用“取大取小”模糊运算和“If…then”型模糊逻辑实现模糊集合的转换。
“取大取小”是针对模糊集合另行定义的、并不是通常集合的运算性质,“取大取小”以信息损失为代价所以不是通常的数值计算,也不能应用数值推理逻辑。
“If…then”型模糊逻辑是针对“取大取小”模糊运算规定的一种推理规则,并不是通常的数值计算逻辑,也不能用于数值计算推理。所以,基于“取大取小”和模糊逻辑实现模糊集合转换是一种专家系统,并不是数学计算。
因为支撑模糊集合转换的不是数学计算,所以模糊数学没有计算(指基于数值推理逻辑的数值计算)。因此,解决模糊数学的问题就是解决模糊数学没有计算的问题,具体讲是解决实现模糊集合转换的数学计算方法问题。
数十年来,人们一直把模糊数学不用数学计算来处理模糊信息的做法,理解为是模糊数学的“特殊性”。只是近年来当人们慢慢意识到处理任何不确定性信息都是“确定的数学计算”的时候,才对模糊数学不用数学计算来处理模糊信息的做法提出质疑。但是,却很少有人从正面研究:模糊集合转换为什么不是线性转换而是非线性转换的原因,更未见从模糊集合转换机理角度研究实现模糊集合转换的非线性计算方法。
所以,要解决模糊数学的问题,就必须揭示模糊集合转换的非线性转换机理,研究实现模糊集合转换的非线性计算方法。
1 解决模糊数学问题的途径
非随机不确定性和随机性的实质性区别是,“不确定性转换”呈现出显著的个性化特点,因而不同类型的“不确定性转换”对应不同的实现转换的数学计算方法。
因为用“取大取小”和“模糊逻辑”这种辅助性支持条件抽象研究实现模糊集合转换的做法使模糊数学偏离了数学计算的轨道,所以,解决模糊数学的问题必须抛开“取大取小”和“模糊逻辑”具体研究实现模糊集合转换的数学方法。
注意到模糊集合是由模糊隶属函数定义的,“模糊集合转换”是基于隶属函数的“不确定性转换”,所以要揭示模糊集合转换机理就不能停留在抽象的“有集不见集”的模糊集合上,而必须回到要求基于隶属函数“定量表征”和基于隶属函数“转换”的、具体不确定性问题中去。只有这样,才能检验基于隶属函数的“不确定性定量表征”是否合理和基于隶属函数的“转换”是怎样意义上的不确定性转换;进而才可能揭示“不确定性转换”的非线性转换机理并具体构建实现“不确定性转换”基于机理的非线性计算方法。这是解决模糊数学问题的惟一途径。
因为本文的重点是揭示“不确定性转换”的非线性转换机理和构建实现“不确定转换”基于机理的非线性计算方法。为此,不再详述基于隶属函数的“不确定性定量表征”,只做简单描述。
2 基于隶属函数的不确定性定量表征
2.1 基于隶属函数定量表征的不确定性
已知影响目标G状态的有m种指标,第j种指标的值域是Uj=[aj,bj],也称Uj为论域。若xj∈Uj,称xj是指标j的监测值。
当指标j取监测值xj时,我们想知道此时目标G属于 Ck(k=1,…,p)状态等级的程度μjk,由于状态的连续性,因而μjk不是只取0与1的二值数而是[0,1]区间上的实数,这样,确定μjk则有无法回避的不确定性(也称模糊性)。
在Uj=[aj,bj]上用构造隶属函数的方法来确定μjk的“不确定性”,那么一旦构造了隶属函数(t)(k=1,…,p,tj∈[aj,bj]),那么 μjk就是函数(t)在点t=xj的函数值,因而是已知的。这样就可用一个向量(μj1,…,μjp)来定量表征当指标j取值xj时,目标原本具有的不确定性状态。
2.2 隶属函数的可测空间结构与代数性质
称μjk=(t)(xj)为指标j取监测值xj时目标G属于Ck状态等级的隶属度,也称μjk指标j的k类隶属度。这样可用隶属度向量
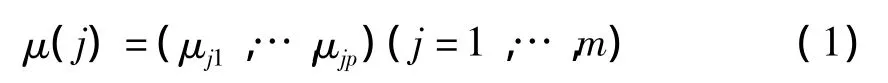
定量表征当j取xj时目标G原本具有的不确定性状态;由“非负性、可加性、归一性”知μjk满足
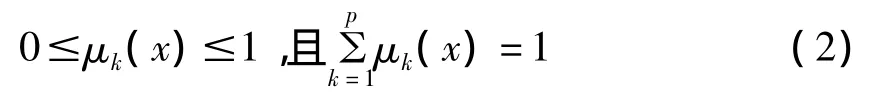
并且m种指标提供的、反映目标G状态的分类信息可表为一个m×p矩阵

称U(G)为目标G的状态转移矩阵。其中j行k列元素μjk意义如前。
显然,目标G的状态转移矩阵U(G)包含了m种指标提供的、反映目标G状态的全部分类信息。
决策目的是,确定目标G在m种指标综合影响下属于Ck状态等级的隶属度μk(G)。
由条件知,目标G的状态由m种指标决定,所以当m种指标提供的、反映目标G状态的分类信息确定后,目标G的状态也随之确定。所以客观上一定存在一种计算方法,可依据G的状态转移矩阵确定目标G属于Ck状态等级的隶属度μk(G)。因为算法是客观存在的,所以一定是机理的。
称确定μk(G)的过程为由指标隶属度到目标隶属度的转换,简称隶属度转换。
到获得目标状态转移矩阵为止,完成了基于隶属函数的不确定性定量表征,并把“不确定性转换”具体化为:从状态转移矩阵出发实现由指标隶属度到目标隶属度的转换。
余下的问题是,揭示隶属度转换的非线性转换机理,并由此构建实现隶属度转换的非线性计算方法。
注1 σ代数A是由状态空间C的一种划分{C1,…,Cp}生成的、对集合的“补运算、可列并运算”都封闭的集合,显然C⊆A。
注2 可测空间是指由状态空间C和C上的σ代数A构成的空间(C,A)。
注3 隶属函数的“非负性”是指,任意xj∈[aj,bj]和σ代数A中任意集合 A,则目标G属于类A的隶属度(xj)满足0≤(xj)≤1。
“可加性”是指,任意 xj∈[aj,bj]和任意 Ai∈A,当 A1∩A2=Ø 时,则
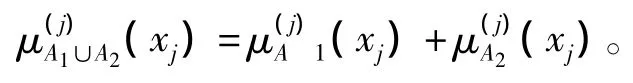
“归一性”是指,任意 xj∈[aj,bj]和任意 Aj∈A,若 Ai∩Ak=Ø(i≠k)且 ∪Ai=C 时,则
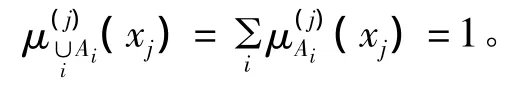
3 隶属度转换的难点分析
1)当m=1时
当只有一种指标j影响目标G的状态时,显然μk(G)=μjk。隶属度转换是直接转换的其合理性在于:指标j提供给目标G的分类信息是目标G所能获取到的惟一也是全部的分类信息。
2)当m≥2时
此时,目标G同时从m种指标那里获得分类信息,如使G属于Ck状态等级的隶属度就有m个不尽相同的数值:μ1k,μ2k,…,μmk,因为我们不知道在确定μk(G)的过程中这m个不同数值之间究竟会产生怎样的“耦合效应”,所以没有理由认为这些不同数值之间的运算一定是线性的,因此无法由μjk具体计算μk(G)。
实际上,我们之所以不知道如何用μjk来计算μk(G),是因为我们不知道在μjk中“是否包含”和“包含多少”对确定μk(G)来说是不起作用的冗余值。
事实上,不管选择怎样的一种算法由μjk来计算μk(G),都必须清除:μjk中可能存在对G分类来说是不起作用的冗余值,否则,计算将无法进行。
那么,怎样才能知道μjk中“是否包含”和“包含了多少”对于目标G分类来说是不起作用的冗余值呢?
为此,进行如下推理与计算。
4 区分权概念及相关定理
4.1 区分权概念
从目标G的状态转移矩阵U(G)出发,进行如下计算。
计算

其中Hj(G)是熵,称ωj(G)是j指标关于目标G的区分权。
显然区分权ωj(G)满足
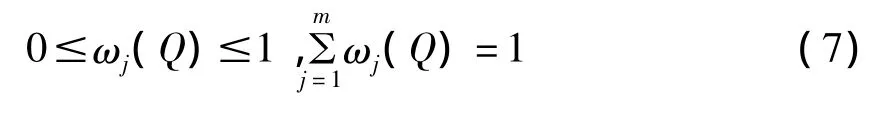
4.2 区分权的意义与作用
区分权的直观意义是,指标j提供给目标G的分类信息能把G所属类别“区分开”的程度。
比如,ωj(G)越大则熵越小,熵Hj(G)越小则μjk对k而言取值越集中,对k取值越集中时说明j提供给G的分类信息越有倾向性,因而对G的分类做出的贡献越大。极端情况是,若ωj(G)取最大值时则熵Hj(G)=0,由熵的性质知此时必有一个μjk=1,其余的全为0;所以j提供给G的分类信息是:单从j看,目标G确定地属于Ck状态等级。显然,此时j对G分类做出最大贡献。
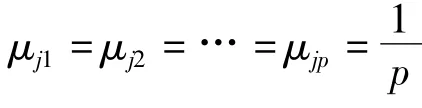
因为当ωj(G)=0时,j提供给目标G的隶属度是对G分类不起作用的冗余隶属度,因而不能参与计算μk(G)。
由此发现一个重要的事实:参与计算目标隶属度μk(G)的并不如直观想象的那样是各j指标的 k 类隶属度 μjk,而是 ωj(G)·μjk。
4.3 基于区分权的相关定理
定理1 如果指标j的区分权ωj(G)=0,则j指标是对目标G分类不起作用的冗余指标。
证明 当ωj(G)=0时,熵Hj(G)=lgp,由熵的性质知此时必有

因为j提供给G的分类信息没有倾向性,所以是对j分类不起作用的冗余信息,因而j是对G分类不起作用的冗余指标。
定理2 (冗余性定理)在目标G的状态转移矩阵中,如果至少有两个行向量对应的区分权不为0,则每种指标提供给G的分类信息中必包含对G分类的冗余值μjk(1-ωj(G))。
证明 因为至少有两种指标的区分权不为0,说明向目标G提供有效分类信息的指标数m≥2。当m≥2时,则区分权ωj(G)<1,所以任一j指标的冗余值μjk(1-ωj(G))都不恒为0。
推论1 指标j提供给目标G的分类信息中不含对目标分类冗余值的充要条件是指标数m=1。
上述论证表明,区分权ωj(G)的实质性作用是滤波,它可滤掉指标隶属度中对目标分类不起作用的冗余值并提取有效值用于计算目标隶属度。
定理3 (非线性转换定理)如果在目标G的状态转移矩阵U(G)中,至少有一个行向量没有取值为1的分量并且至少有两个行向量对应的区分权不为0,那么,由指标隶属度到目标隶属度的转换必是非线性转换。
证明 因为状态转移矩阵U(G)中至少有一个行向量没有取值为1的分量,说明不会因为每个行向量都有一个分量为1其余分量均为0而使确定区分权的计算都退化为线性计算;又因为至少有两个行向量对应的区分权不为0,说明在m种指标中至少有两种向目标G提供有效的分类信息,说明影响目标状态的指标数不会退化为m=1而使隶属度转换简化为直接转换。所以,在定理条件下,由指标隶属度到目标隶属度的转换是非线性转换。
推论 如果状态转移矩阵U(G)中,每一个行向量都是表示“确定状态”的向量(即每个行向量都有一个分量μjk=1而其余分量均为0),则由指标隶属度到目标隶属度的转换是线性转换。
该推论的价值在于它揭示了一个基本事实:隶属度转换的非线性源于单指标下目标状态的不确定性。它揭示了在非随机不确定性理论中,不确定性转换与非线性之间的联系。
5 隶属度非线性转换算法与转换模型
从目标G的状态转移矩阵出发,计算目标隶属度的步骤如下:
步骤1 由公式(4)、(5)、(6)计算指标区分权ωj(G)。
步骤2 计算
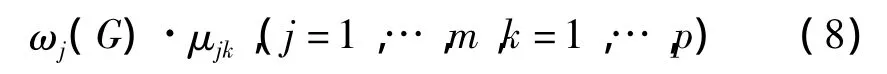
称ωj(G)·μjk是j的k类有效值。
步骤3 计算

称λj(G)·ωj(G)·μjk是j的k类可比值,其中λj(G)是j指标关于目标G影响的重要性权重,并满足:

之所以用j的重要性权重压缩j的k类有效值ωj(G)·μjk,是为了保证压缩后得到的“λj(G)·ωj(G)·μjk”对不同的j指标具有可比性和直接可加性。
步骤4 计算
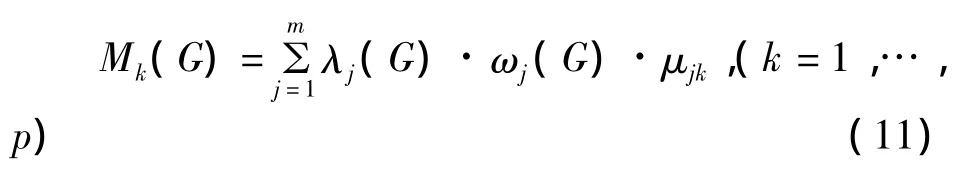
称Mk(G)是目标G的k类可比和。
显然,Mk(G)越大时说明目标G属于Ck类的可能性越大。
步骤5 计算并定义
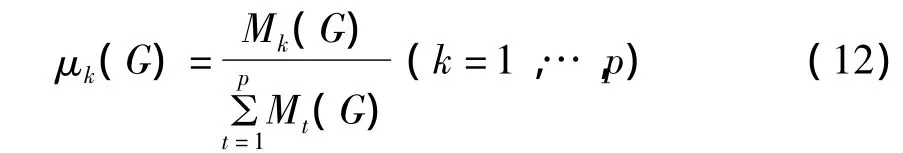
显然由(11)式定义的μk(G)满足:
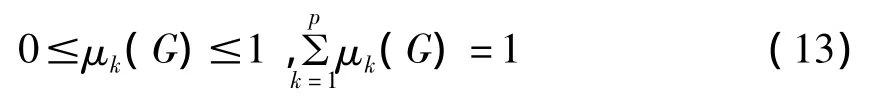
所以μk(G)是目标G属于Ck类的隶属度。
至此,从目标G的状态转移矩阵出发,经过5个步骤确定了目标隶属度μk(G),实现了由指标隶属度到目标隶属度的转换。转换模型记为M(1,2,3);其中“1”表示区分权滤波,“2”表示将有效值转换为可比值,“3”表示由可比值实现隶属度转换。
上述从状态转移矩阵出发实现隶属度转换过程,不需要增加任何先验知识和辅助性支撑条件,也不造成已知的分类信息损失或信息失真,用的工具是基于数值推理逻辑的数值计算。显然这与通过增加“取大取小”运算与“If…then”型模糊推理逻辑等辅助支撑条件实现模糊集合转换的做法是本质不同的。
推论 如果状态转移矩阵U(G)中每个行向量都表示确定状态(即每个行向量中都有一个分量 μjk=1其余分量均为 0),则 M(1,2,3)模型将退化为“加权平均”模型M(·,+)。
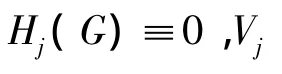
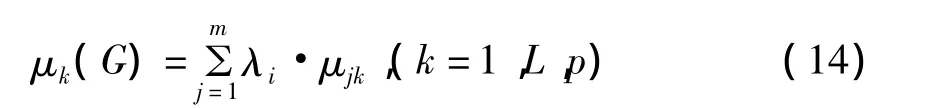
这就是熟知的“加权平均”模型M(·,+)。
推论的价值在于,从计算机理上证明,“加权平均”线性模型正确性的条件是:单指标下表征目标状态的“归一化”向量都是表示“确定状态”的向量(即向量中有一个分量为1其余分量均为0)。
实际上,由于诸多不确定因素的影响,目标在单指标下的状态通常都是“不确定的”,表现在:当用一个“归一化”向量定量表征这种“不确定性”状态时,向量中没有取值为1的分量。
但是,实际应用中,绝大多数都是把线性的“加权平均”模型用于实现“不确定性”状态转换[1-5]。
6 应用例
某惯性导航系统仿真可靠性评价指标体系,构成一个如表1所示的三层递阶层次结构。由于确定底层指标所属评价等级的程度具有无法回避的内在不确定性,所以基于层次分析法的多级模糊模型,成为优势评价模型。
文献[1]用层次分析法确定二、三层指标的重要性权重,见表1中各项指标后括号中的数字;评价分为“高、较高、一般、低”4个评价等级,分别用C1,…,C4表示;统计专家评分,并根据评分构造规范隶属函数的方法,确定各项底层指标关于4个评价等级的隶属度向量,见表1中最后一列的4维向量。在表1中所示条件下,试确定该惯性导航系统仿真可靠性的评价等级。
易见,由结构下层被支配指标隶属度确定结构上层支配指标隶属度,都是M(1,2,3)模型的一次实现。基于M(1,2,3)模型的评价步骤如下:
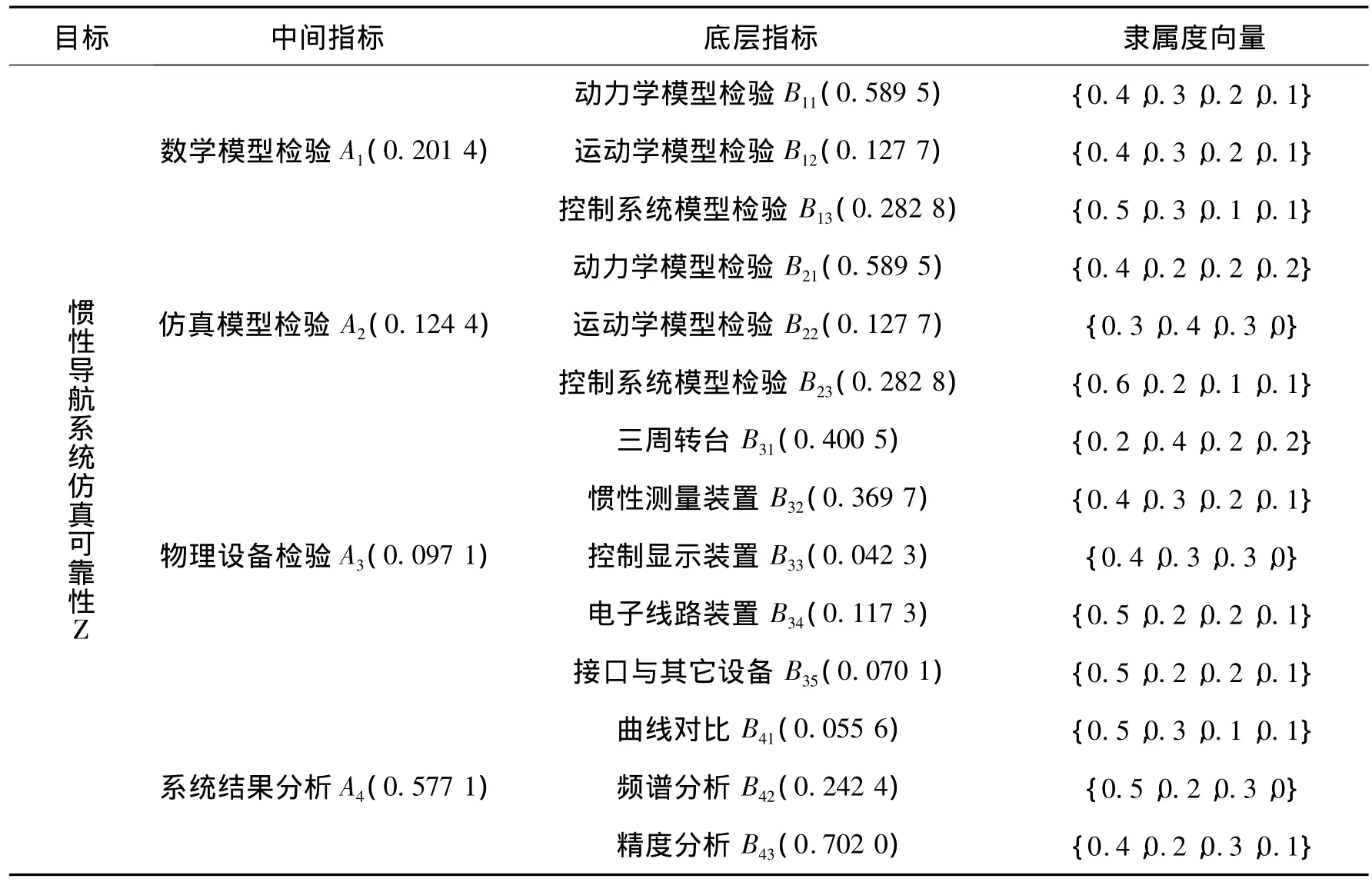
表1 惯性导航系统仿真可靠性评价指标体系[1]Tab.1 Reliability evaluation hierarchical structural of simulation for INS
步骤1计算中间指标的隶属度向量。以计算A1(数学模型检验)的隶属度向量为例。
A1的状态转移矩阵为

由 U(A1)经 M(1,2,3)的计算得,A1的隶属度向量为 μ(A1)=(0.444 7,0.300 0,0.155 3,0.100 0)。同理可得 A2、A3、A4的隶属度向量 μ(A2)、μ(A3)、μ(A4),连同 μ(A1)一并构成系统仿真可靠性Z的状态转移矩阵U(Z)

步骤2计算顶层总目标Z的隶属度向量。依据矩阵U(Z),按照与(1)同样步骤可得的隶属度向量为
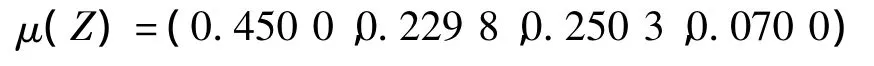
步骤3识别。因为可靠性等级划分有序,如Ck类优于Ck+1类,所以适用于无序划分的最大隶属度识别准则不适用,改用置信度识别准则[6]。
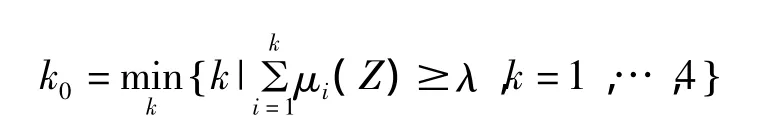
设 λ(0.5<λ <1)为置信度,计算则判 Z属于 Ck0评价等级,且有不低于 λ的置信度。
本例中判Z属于C2等级并且有不低于67%(0.45+0.229 8 >0.67)的置信度。
7 结论
1)当用构造规范化隶属函数的方法确定目标在单指标监测值下属于Ck状态等级程度的不确定性,进而用隶属度向量定量表征目标在单指标下的不确定性状态,则可把模糊数学中通过模糊集合转换来确定目标在多指标下的不确定状态具体化为实现由指标隶属度到目标隶属度的转换。
2)隶属度转换是非线性转换,通过揭示隶属度转换的非线性转换机理构建实现隶属度转换的非线性数学计算方法,不但处理了模糊信息,也展现了模糊数学本应具有的数学计算。
3)如果只是表征和处理模糊信息,则未必需要采用隶属函数去定义一种“有集不见集”的模糊集合概念,至少不用为了实现模糊集合转换去人为规定一种“取大取小”模糊运算和“If…then”型模糊逻辑,因为后者正是导致模糊数学失去计算的原因。
[1]要瑞璞,沈惠璋,刘铎.多层次系统的综合评价方法研究[J].系统工程与电子技术,2005,27(4):656-658.
[2]郑贤斌,陈国明.基于FTA油气长输管道失效的模糊综合评价方法研究[J].系统工程理论与实践,2005,25(2):139-144.
[3]马国忠,米文勇,刘晓东.民航系统安全的多级模糊评价模型[J].西南交通大学学报,2005,42(1):104-109.
[4]冀红娟,杨春和,张超,等.尾矿库环境影响指标体系及评价方法及其应用[J].岩土力学,2008,29(8):2087-2091.
[5]王大伟,冯英俊.模糊多级综合评价模型与应用[J].系统工程与电子技术,2006,28(6):867-868,910.
[6]程乾生.属性识别理论模型及应用[J].北京大学学报:自然科学版,1997,33(1):12-20.
