直觉模糊层次分析法

2011-06-05高红云哈明虎

河北工程大学学报(自然科学版) 2011年4期

高红云，王超，哈明虎，3

（1.河北大学管理学院，河北保定 071002;2.河北大学物理科学与技术学院，河北保定 071002;3.河北工程大学经管学院，河北邯郸 056038）

层次分析法是Saaty［1］提出的一种定性和定量分析相结合的多准则系统分析决策方法。层次分析法通过明确问题，建立层次结构模型，构造判断矩阵，层次单排序和层次总排序五个步骤计算各层次构成要素对于总目标的组合权重，从而得出不同可行方案的综合评价值，为选择最优方案提供依据［2］。在综合评判各因素权重分配时，层次分析法仅凭经验根据因素的重要性直接给出权重值，或仅考虑专家判断的两种极端情况，而没有考虑专家判断的模糊性，难以做到客观准确［3］。基于此，一些学者在Zadeh［4］建立的模糊集理论基础上将模糊思想和方法引入层次分析法中，提出了模糊层次分析法［2］，并已成功应用于投资决策等领域［5］。然而，模糊层次分析法在一些现实决策问题中存在一定的局限性。例如，模糊层次分析法中的模糊集能在一定程度上表示决策者对研究对象的主观判断，但不能精确表达弃权或犹豫不决的情况。为了解决此类问题，Atanassov［6－7］在Zadeh的模糊集的“亦此亦彼”的模糊概念基础上增加了一个新的参数—非隶属函数建立了直觉模糊集，在处理上述不确定性方面更具灵活性和实用性。本文将直觉模糊集思想应用于层次分析法中，建立了直觉模糊层次分析法，扩充和发展了模糊层次分析法。

1 直觉模糊集相关知识

定义1［6－7］假设 X 是一个非空经典集合，A={＜ x，μA（x），vA（x）＞ |x∈X}，X={x1，x2，…，xn}的三重组称为直觉模糊集，其中 μA（x），vA（x）分别表示X中的元素x属于X的隶属度和非隶属度。且 μA∶X→［0，1］，vA∶X→［0，1］，0≤μA（x）+vA（x）≤1，x∈X。在X的每一个直觉模糊集中称 πA（x）=1－μA（x）－vA（x）为x属于X的犹豫度即不确定程度，且0≤πA（x）≤1，x∈X。

定义 2［6－7］设 a1，a2是一个给定的论域上的两个直觉模糊数，其中 a1=（μ1，v1），μ1∈［0，1］v1∈［0，1］并且 μ1+v1∈［0，1］;a2=（μ2，v2），μ2∈［0，1］，v2= ∈［0，1］并且 μ2+v2∈［0，1］，并设 λ为实数且λ≥0，定义直觉模糊数的运算如下:

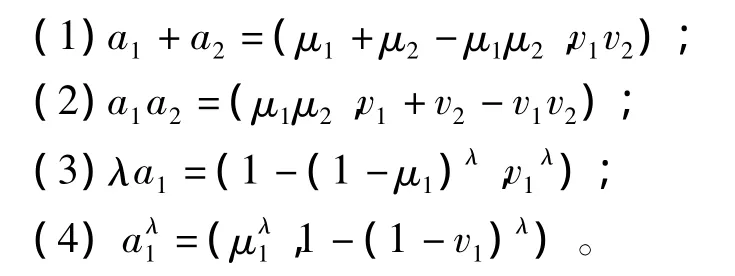
定义3为了得到权重大小比较，我们定义了新的得分函数为

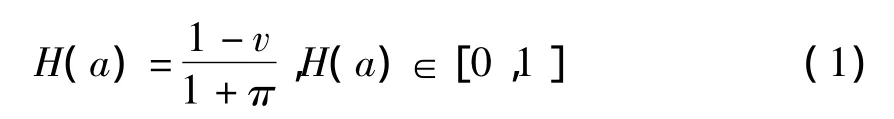
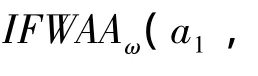
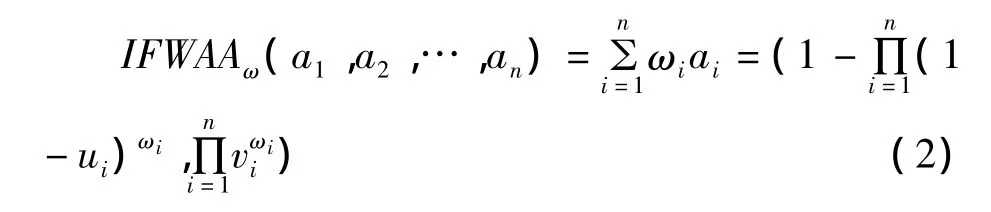
2 直觉模糊层次法模型

2.1 建立层次结构体系

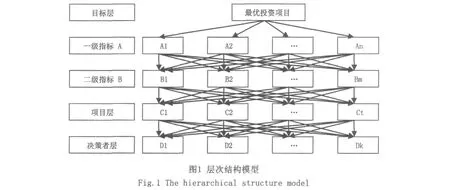
对于项目的决策需要考虑很多因素，将其影响因素进行分层得到层次结构模型，如图1所示。

2.2 建立直觉模糊互补判断矩阵

定义5直觉模糊层次分析中，对属性之间进行两两比较其重要程度得到直觉模糊判断矩阵A=（aijm×n，aij=（μij，vij，（i，j=1，2，…，n），称为直觉模糊互补判断矩阵，若满足如下性质:

1）μii=0.5，i=1，2，…，n。

2）若 aij=（μij，vij），aij=（μji，vji），i，j=1，2，…，n;则必有 μij+μji=1。

为了对属性之间的重要程度进行定量的描述，我们可以定义标度，如表1所示。

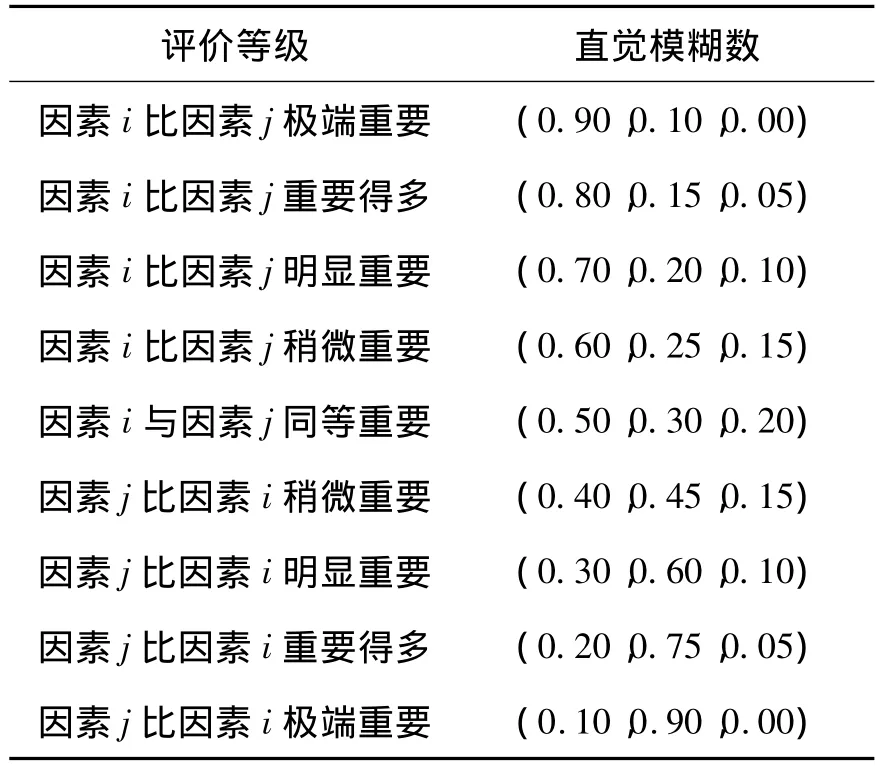
表1 属性重要程度定义的标度表Tab.1 Table of scale the importance of the attribute

2.3 直觉模糊互补判断矩阵的一致性检验

直觉模糊互补判断矩阵的一致性检验直接根据隶属度构成的判断矩阵的一致性检验得到。根据徐泽水［9］推导出的求解模糊互补判断矩阵权重的公式来求解权重

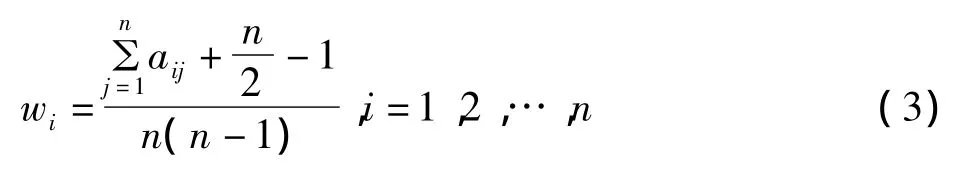
并利用文献［10］推导出的相容性来检验权重公式的合理性。

定义 6 设矩阵 A=（aij）m×n，B=（bij）n×n均为模糊判断矩阵，则称A和B的相容性指标为

当相容性指标I（A，A*）≤0.1时，认为判断矩阵A为满意一致的。进而，我们近似地认为相应的直觉模糊判断矩阵也是一致的。

2.4 直觉模糊判断矩阵权重确定

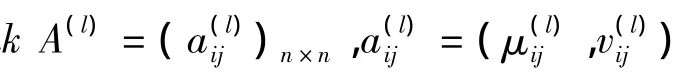
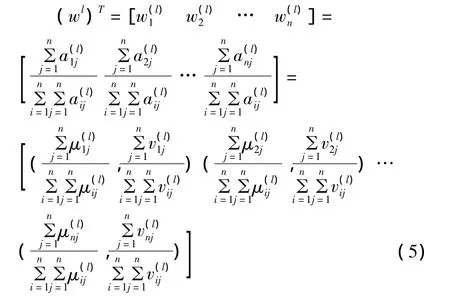
根据式（2）进行直觉模糊加权计算得

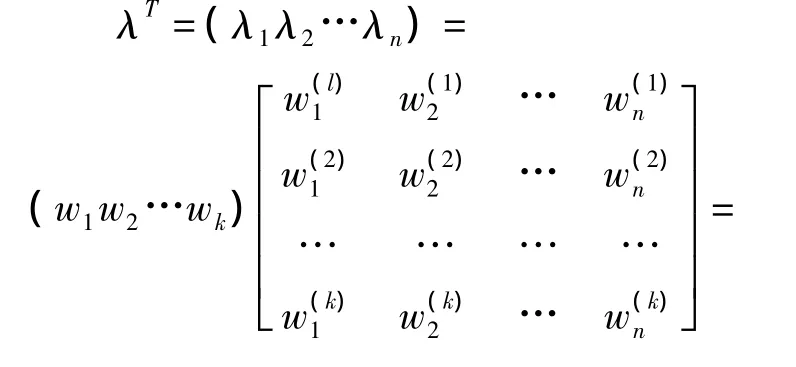
2）二级属性综合权重确定。设k个专家对二级指标属性i与j对于一级属性指标r（r=1，2，…，n）的重要程度的直觉模糊判断矩阵为=（）m×m，=）i，j=1，2，…，m，（l=1，2，…，k;r=1，2，…，n），其中、分别表示决策者l对二级属性i与j相比较的重要和不重要程度。

由（4）求出二级属性对一级属性的加权相对权重为 σ =（σij）t×m，σij=（μij，vij，l=1，2，…，t;j=1，2，…，m。

根据（5）一级属性权重对二级属性综合加权到二级属性的综合属性值为σ（2）=（σ（1））Tσ。

由公式（6）、式（7）求得二级指标的综合权重为（σ（2））T=（σ1，σ2，…，σm）。

2.5 最终评价计算

假设有t个可供选择的项目方案，有k个专家根据二级属性对这些方案进行决策得到k个直觉模糊判断矩阵=（）m×k，=，），i=1，2，…，m，j=1，2，…，k，l=1，2，…，t。

3 算例

假设有3个专家对三个经济开发区的风险投资项目的风险大小进行评价，假设专家的评价权重为（0.5，0.3，0.2）。

第一步:建立风险层次结构图。假设一级属性指标包括三个:技术风险、市场风险、管理风险;二级指标包括四个:资源环境、设计施工、政策风险、管理组织。

第二步:一级属性权重确定。三个专家对一级属性指标两两重要程度评价矩阵如下:

二级指标相对于一级指标A1相互比较的重要程度评价矩阵为

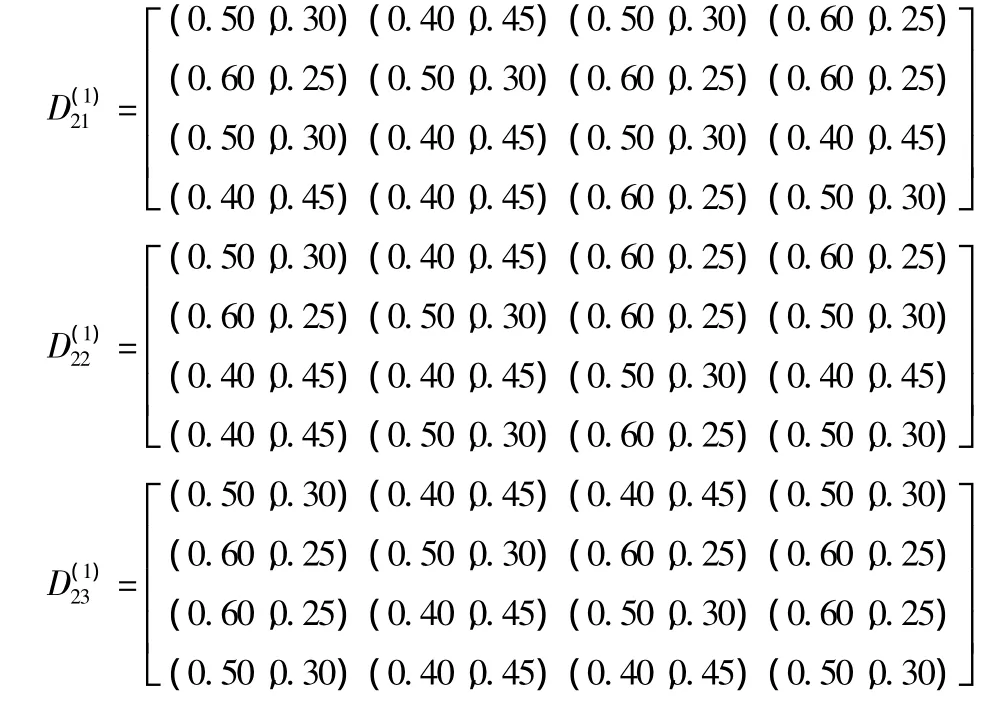
二级属性相对于一级属性A2两两比较评价矩阵为

二级属性相对于一级属性A3两两比较评价矩阵为

各决策者对项目关于二级属性满足程度评价矩阵为

属性加权计算得

第三步:利用上述直觉模糊层次分析步骤进行决策。

首先，一级指标的重要程度的语言变量转化为直觉模糊数并计算得到一级属性单因素直觉模糊权重为（σ（1））T= ［（0.340 1，0.319 6）（0.373 5，0.271 8）（0.286 8，0.406 2）］，计算得分并归一化得到以及属性权重为（σ（1））T=（0.338 5，0.358 5，0.303 0）。

然后根据上述评价判断矩阵通过计算得到二级属性的单因素决策加权后权重向量矩阵: