智能桁架作动器数目与位置的多目标优化
2011-06-05张世君张京军何丽丽高瑞贞
张世君,张京军,何丽丽,高瑞贞
(1.河北工程大学 土木学院,邯郸 056038;2.河北工程大学机电学院,邯郸 05603)
桁架结构在太空中运行时,受空间环境等因素的影响,不可避免的产生结构变形,影响航天结构的精度。近年来出现的层叠型压电作动器由于体积小、工作电压低、位移量大等特点在智能桁架中得到广泛应用。然而,在智能桁架中如何布置合适的作动器数目与位置是多目标优化问题,任建亭[1]、咸奎成[2]采用固定加权系数方法优化此类多目标问题。但由于各个目标的权重系数由人为确定,所以优化的结果存在着主观性。基于遗传算法的随机权重方法[3]通过遗传算法随机的确定各目标的权重系数,可以在一定程度上避免人为因素影响产生的优化偏差,王晓晴[4]等将随机权重应用于生产系统多目标决策问题,李瑞敏[5]等将随机权重方法运用在交通多目标控制方面。本文基于随机权重的方法优化智能桁架作动器的数目和位置,以减少固定加权系数方法存在的人为主观性,并对遗传算法进行改进,以加快遗传算法的收敛速度。
1 模型建立
层叠型压电作动器由多个几何物理参数相同的压电陶瓷片组成(图1),作动器中的各个压电陶瓷片采用并联电路(图2),既有一定位移输出量,又可以承受一定的荷载。设作动器中的压电陶瓷片共有s个,则在理想情况下总的位移输出Δ为

基于式(1)可以推出压电作动器内部轴向力为


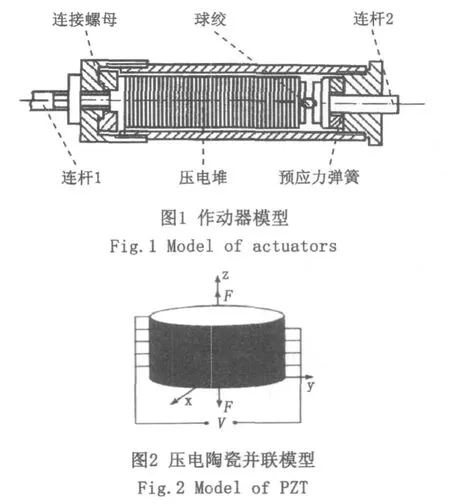
压电桁架中各个杆件在外荷载和电压下的承受的力为

式中 Fi,u—杆件 i的总轴力;Fi,0—杆件 i仅在外荷载作用时的轴力;a—作动器的位置变量,当a=1或ai=0时分别表示杆件i处布置和不布置作动器,∑ai(i=1,2,…,n)表示配置的作动器数目。
普通桁架节点位移公式[6]为

基于式(3)得压电桁架节点位移公式为

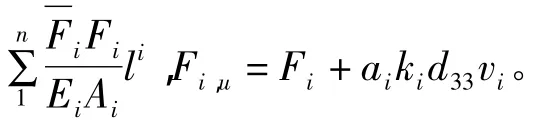
将式(3)带入式(5)得:
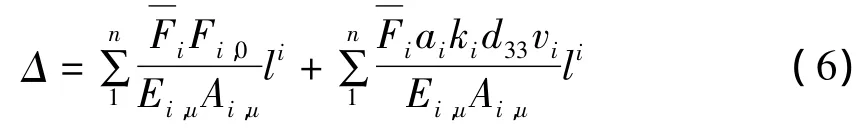
桁架节点偏离平衡点越小则桁架的变形越小,因此位移的目标函数应为位移的模,即abs(Δ)。作动器优化配置的数学模型可表示为
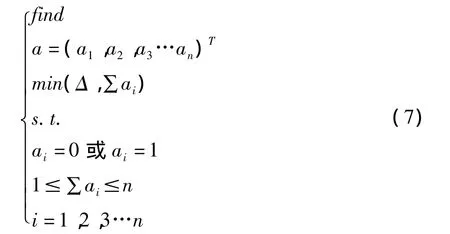
2 多目标求解
压电桁架作动器数目和位置优化的理想结果是,作动器配置数目和节点位移最小,且作动器在桁架中布置的位置最优。然而桁架中配置的作动器数目和位置影响结构节点位移,相应的结构位移的大小又影响配置的作动器数目和位置,因此桁架作动器的数目和位置优化是多目标优化问题。传统的固定权重方法由人为确定各个目标的权重系数,存在很大的主观性。随机权重的方法通过随机的方法生成各个目标函数的权重系数,并且每计算一次目标函数f(x)便随机的产生新的一组权重系数,从而在很大程度上避免了主观性。计算公式如下

式中ri、rj—非负随机数;P—多目标的数目。将多目标转化为单目标后目标函数为

3 遗传算法应用与改进
遗传算法是依据达尔文的生物进化论为启发,基于优胜劣汰、适者生存的一种优化方式,包括编码、适应度计算、选择、交叉、变异等过程。遗传算法具有对问题依赖小,依据概率来指导搜索方向等特点,但也存在收敛过程慢和早熟等诸多问题[7-8],本文针对遗传算法早熟和收敛迟钝的问题对选择算子进行改进。
3.1 编码与解码
编码是遗传算法首先要解决的问题,也是遗传算法设计的关键步骤。本文根据优化问题的特点采用二进制编码,按桁架的杆件编号从左到右排列染色体基因码,编码的长度为桁架中杆件的数目。以12杆桁架(如图3)为例,个体的染色体长度为杆件的数目12,如果经过编码得某个个体的染色体为100001011000,则表示智能桁架共布置4个作动器,位置分别为1、6、8、9杆件处。
3.2 适应度
遗传算法的适用度表示群体中各个个体在优化计算中能达到或有助于找到最优解的优良程度。适应度较高的个体遗传到下一代的概率较大,而适应度较低的个体遗传到下一代的概率相对较小。
本文将适应度函数定义为:

3.3 遗传算子改进
遗传算法中有选择、交叉和变异3个算子。其中,选择算子通常是根据适应度大小采用轮盘选择的方式进行选择,但容易引起早熟和搜索迟钝等问题。本文在轮盘选择的基础上对选择算子进行改进,当判断各个染色体过于近似时增大变异概率,从而产生不同数目的大量后代,增加基因的多样性。
交叉操作是遗传算法中主要的遗传操作之一,通过交叉可以得到新一代个体,而新个体中组合了父代的个体特征。交叉操作的过程是以群体内的各个个体为父代随机搭配成对,并对搭配成对的父代个体之间以一定的概率交换部分染色体,形成的新个体为子代,具体如下:
父代A:10010|0101|101
父代B:00110|1001|001
子代 A':10010|1001|101
子代 B':00110|0101|001
变异是对群体中的每一个个体,以一定变异概率改变一个或某一些基因座上的基因值为其他的等位基因,形成的新的个体为子代,具体如下:
父代C:110011011101
子代 C':111010011101
4 算例
12杆的平面桁架,左端铰接,右端自由(图3)。杆件材料弹性模量为70 GPa,允许应力为±20 MPa,各杆件横截面积均为1 cm2。作动器材料弹性模量为72 GPa,采用40片压电陶瓷组成压电陶瓷堆,允许轴力为2 kN,作动因子为6×10-10m/V,允许电压为150 V,外荷载100 N作用在节点5,方向向下。

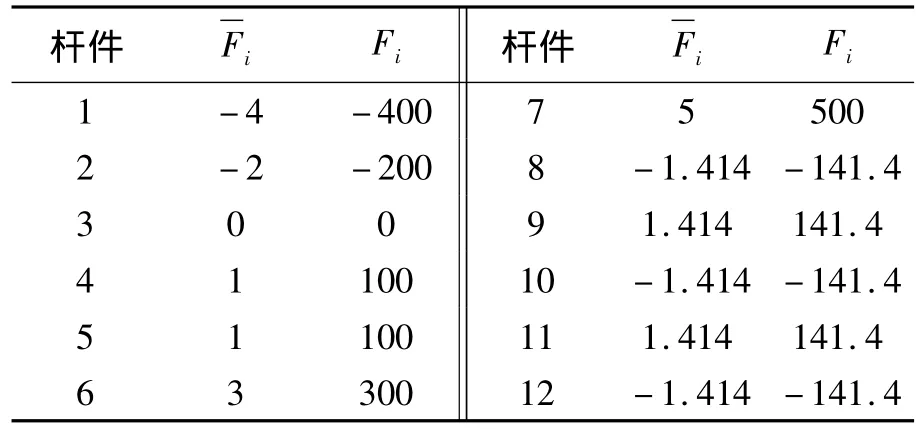
表1 杆件轴力Tab.1 Axial force of every bar N

5 结论
1)运用随机权重的方法将智能桁架作动器数目与位置的多目标优化问题转化为单目标优化问题,避免了固定权重系数方法存在的人为因素影响。
2)在轮盘选择的基础上对遗传算法的选择算子进行改进,当判断各个染色体过于近似时增大变异概率,从而产生不同数目的大量后代,增加基因的多样性。应用改进后的遗传算法对智能桁架作动器数目与位置的多目标优化问题进行求解,收敛速度快,繁殖代数少,有较好的计算效率。
[1]任建亭,闫云聚,姜节胜.振动控制传感器/作动器的数目和位置优化[J].振动工程学报,2001,14(2):237-241.
[2]咸奎成,黄 海.自适应压电桁架形状控制中作动器优化配置[J].北京航空航天大学学报,2007,33(5):527-530.
[3]CHENG R,M GEN.A survey of genetic multi-objective optimizations[R].Ashikaga:Ashikaga Institute of Technology,1998.
[4]王晓晴,唐加福,宫俊,等.基于随机权重多目标遗传算法的多目标动态单元构建方法[J].管理学报,2008,5(4):16-52.
[5]李瑞敏,陆化普.基于遗传算法的交通信号控制多目标优化[J].长安大学学报:自然科学版,2009,29(3):85-88.
[6]龙驭球,包世华.结构力学Ⅰ[M].3版.北京:高等教育出版社,2006.
[7]李京涛,何丽丽,高瑞贞,等.改进遗传算法在桁架拓扑优化中的应用[J].河北工程大学学报:自然科学版,2009,26(3):19-21.
[8]陈焕,范志红,高瑞贞,等.基于不动点算法和K2(m)剖分的遗传算法的改进[J].河北工程大学学报:自然科学版,2011,28(2):56-59.
