基于熵权法和灰色关联度分析的轴承故障诊断
2011-06-05林巨广严军富
林巨广, 严军富, 关 鹏
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
据统计,变速器故障的30%是由轴承故障引起的,而轴承故障中90%的故障主要来自内外圈的故障[1-2]。轴承发生故障时其振动信号的特征参数(如时域峭度系数、裕度指标和频域功率谱重心等)都会产生相应的突变,可以将这些参数构成模式向量,通过灰色关联度分析方法识别轴承的故障状态[3]。
多参数诊断中不同参数对不同故障反映出的效果不一样,本文在传统的灰色关联度基础上,引入熵权理论确定轴承各种故障状态下各参数指标的权重系数,获得了满意的诊断结果。
1 轴承信号的时频无量纲参数
利用振动信号的时域和频域无量纲特征参数的监测可以识别轴承的内、外圈和滚动体故障。
1.1 时域特征参数
时域中应用较多的特征参数有峰值指标、峭度系数、裕度指标和波形指标等。峰值指标反映了信号的峰值变化程度,正常信号的峰值指标为3~5,峰值过大时往往对应着某一局部缺陷。峭度系数反映了信号偏离正态分布的程度,正常轴承信号其幅值呈现正态分布,峭度系数值为3,峭度系数过高反映了局部缺陷。峭度系数、裕度指标对于冲击脉冲类故障比较敏感,特别是当故障早期发生时,有明显增加;但上升到一定程度后,随故障的逐渐发展,反而会下降,表明它们对早期故障有较高的敏感性,但稳定性不好。而峰值系数的稳定较好,但对早期故障信号不是很敏感。
1.2 频域特征参数
功率谱反映了信号中的频率成份以及各频率成份的能量大小情况,当信号中各频率成份的能量比发生变化时,功率谱主能量的谱峰位置也将发生变化,另一方面,当信号的频率成份增多时,功率谱上能量分布将表现为分散;当信号中频率成份减少时,功率谱上能量分布将表现为集中。通过描述功率谱中主频带位置的变化以及能量的分散程度,可以较好地描述信号频域特征的变化[4]。频域中用于描述这些变化的特征参数有功率谱重心、功率谱方差和谐波因子等。功率谱重心指标反映了功率谱重心位置的变化程度,正常状态下功率谱重心位于低频区。当出现局部故障时,冲击振动激起系统的固有振动,使得功率谱重心位置向右偏移。功率谱方差反映了谱能量分布的分散程度,功率谱各幅值越靠近谱重心分布方差值越小。谐波因子综合反映了谱分布状态和谱宽情况。将时域与频域参数互相配合弥补各自的优缺点,可以有效地监测轴承的故障信息[5]。
2 灰色关联度分析
将滚动轴承的状态看作一灰色系统,其关联度分析的基本思想是依关联度的大小进行故障判别,若待检轴承与某一典型故障的关联度最大,则将待检轴承归入该类故障。轴承关联度分析步骤[6]如下。
(1)分别从正常和故障轴承的振动信号中提取特征参数Xi,构成特征向量矩阵作为标准,故模式Di为:
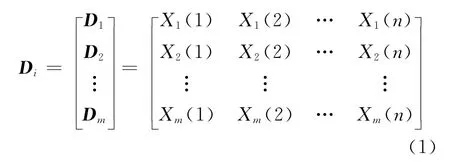
其中,m为选取的故障类型数;n为特征参数。
(2)测取待检轴承的故障特征参数XT构建待检模式DT为:
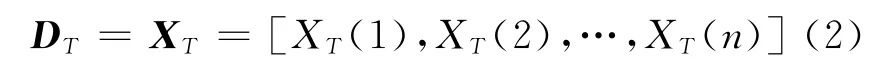
(3)计算待检模式与标准模式中各种故障类型的关联度ri,定义:
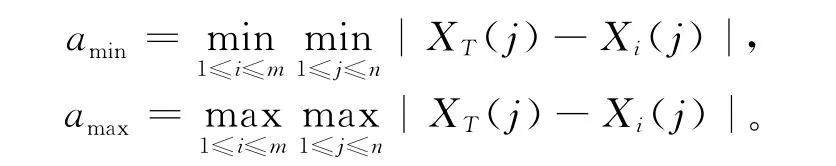
DT与Di的关联度系数Ci为:
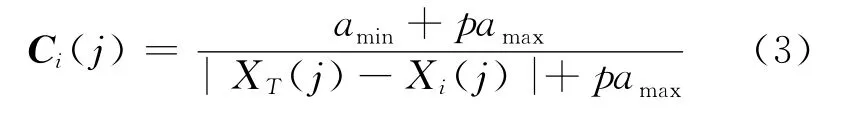
其中,p为分辨率系数,p∈[0,1],p取值反映了特征参数整体上对关联度的影响程度,本文按照文献[4]的规则选取p。
由此可得出,到待检模式DT与标准模式Di的加权关联度ri为:
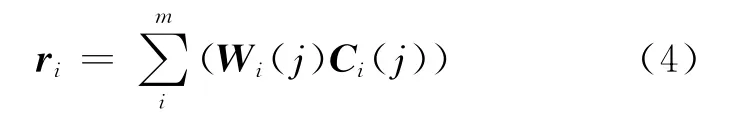
其中,Wi(j)为故障类型i的特征参数的权重,目前常用的权系数确定方法有AHP法、Deplhi法、专家评分法[7]等,但这些主要是通过人们对指标的重要性判断来定权,重要性越高,权数越大,受主观因素的影响较大,客观性较差。因而本文采用熵权法,从实际试验数据中提取各指标的权重系数。
3 熵权法
熵权法的基本思想是依据指标变异性的大小来确定客观权重[8-9]。一般来说,某个指标的信息熵Ei越小,表明指标值的变异程度越大,所能提供的信息量越多,在诊断分析中所起的作用越大,其权重也越大。相反,某个指标的信息熵Ei越大,表明指标值的变异程度越小,提供的信息量越少,在综合评价中所起的作用越小,其权重也越小。假设有m个评价指标、n个评价对象的实际数据,将其归一化后转变为标准化数据{dij},定义其第i个指标的熵为:
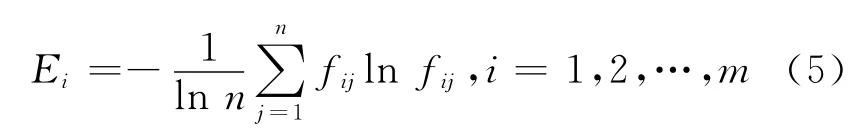

将(6)式代入(4)式中得到基于熵权的灰色关联度模型。
4 实例分析
本文引用美国Case Western Reserve提供的6205轴承振动信号,该轴承的滚动体平均直径7.94mm,轴承节圆直径39mm,滚动体数为9,试验中轴承输入转速1 797r/min,采样频率48kHz。通过电火花加工(EDM)方法在轴承内外圈及滚动体上加工出0.18、0.36、0.54mm 3种尺寸的故障孔,用以模拟轴承的局部故障信息。正常和内圈、外圈及滚动体处各存在0.18mm故障尺寸的时域振动信号如图1所示。
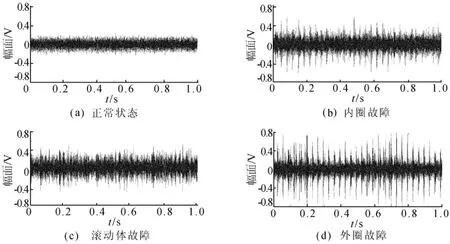
图1 轴承的4种故障状态振动信号
试验中先对原始信号进行小波降噪后,选取峰值指标、峭度系数、裕度指标、波形指标、功率谱重心、功率谱方差和谐波因子这7项参数作为灰色关联度的诊断指标。
先取一组包含正常、内圈(故障尺寸0.18mm)、滚动体(故障尺寸0.18mm)和外圈(故障尺寸0.18mm)4个轴承数据作为标准模式,再取另一组包含正常、内圈(故障尺寸0.36mm)、内圈(故 障 尺 寸 0.54mm)、滚 动 体 (故 障 尺 寸0.36mm)、滚动体(故障尺寸0.54mm)、外圈(故障尺寸0.36mm)和外圈(故障尺寸0.54mm)7个待检轴承组成待检模式。从振动信号中提取这2组信号的时频无量纲特征参数,按文献[10]中的0-1归一化方法处理,结果见表1和表2所列。

表1 标准模式的特征参数
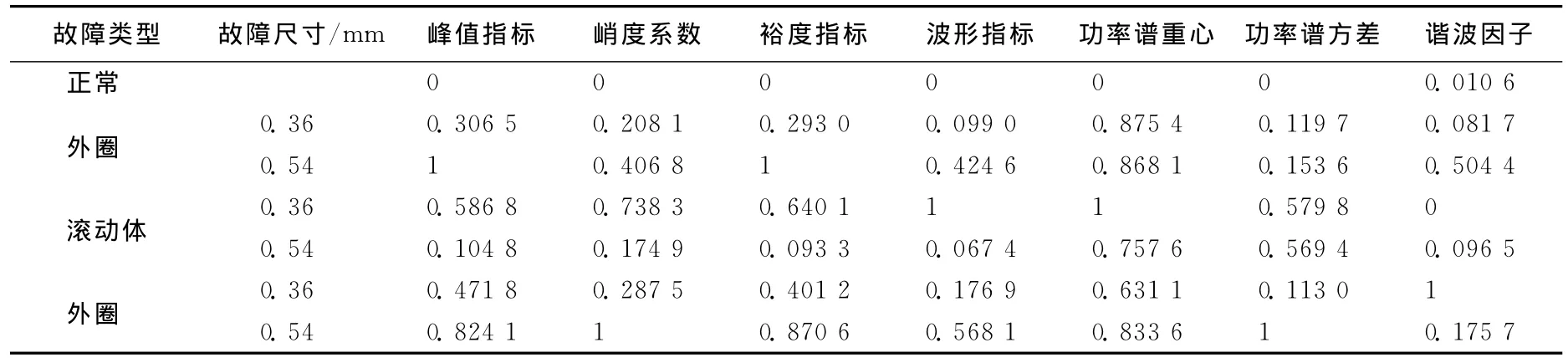
表2 待检模式的特征参数
正常状态下各参数都很小,熵值变化较小,各指标的熵权接近平均值,为简化计算步骤,将正常状态的权系数按照均值化处理。针对轴承的3种故障状态,共需设置3组熵权重系数,限于篇幅,本文给出内圈故障状态的熵权重系数确定方法(滚动体故障和外圈故障状态的熵权重系数都是按照相同的方式确定)。熵权法依赖于对试验样本的客观性分析。
本文抽取了7组内圈故障的轴承试验数据记为内圈故障1~7,其中内圈故障1~3为3组内圈(故障尺寸0.18mm)的数据,内圈故障4~5为2组内圈(故障尺寸0.36mm)的数据,内圈故障6~7为2组内圈(故障尺寸0.54mm)的数据,对数据归一化处理构建特征向量见表3所列,按(5)式计算各指标的熵值E为 {0.987 2,0.985 0,0.983 2,0.985 7,0.984 2,0.987 4,0.988 9},按熵值理论,指标的熵值越大,代表该指标对内圈故障程度识别的灵敏度越小。将上述计算熵值代入(6)式得到内圈故障的权重系数W为{0.130 1,0.152 7,0.170 6,0.144 9,0.161 0,0.128 2,0.112 5},同样的方法得到滚动体和外圈故障的熵权重,见表4所列。
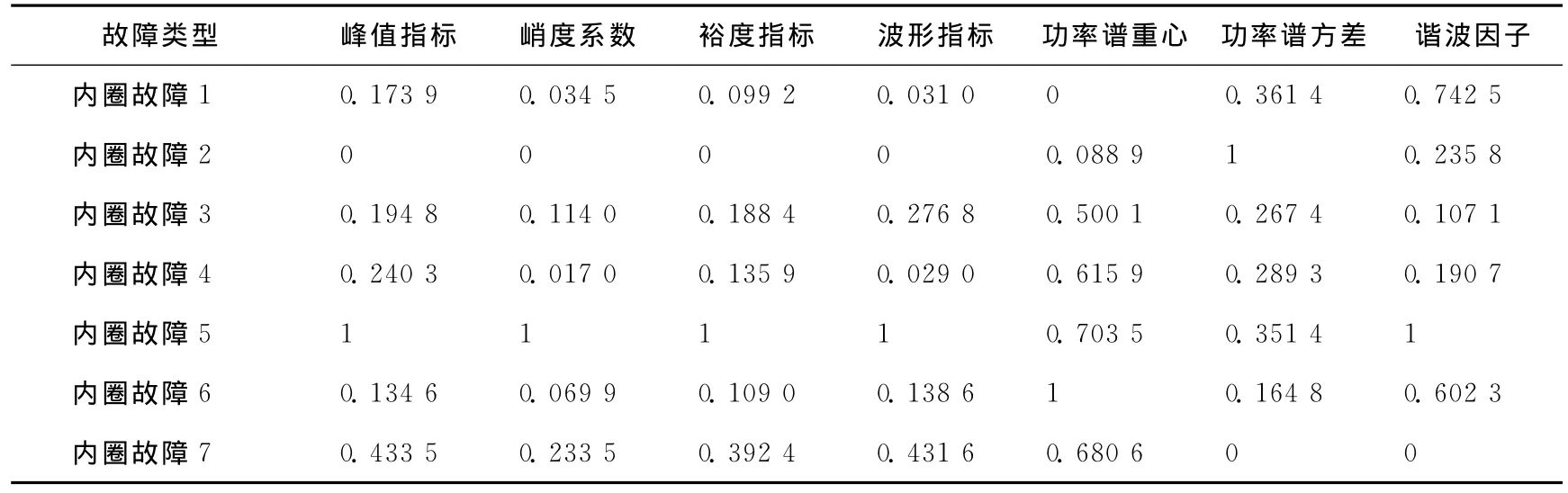
表3 轴承内圈故障的数据样本

表4 轴承故障模式的熵权重
将求得的权系数代入(4)式中,参照文献[2]设置的分辨率系数,按照灰色关联度理论计算选取的7种待检状态与标准故障的关联度,见表5所列。未采用权系数修正的传统A型关联度分析结果见表6所列,从表6可以看出,滚动体故障尺寸0.54mm的诊断结果存在误判,究其原因可能是随着滚动体故障程度的扩大,部分特征参数如峭度系数、裕度指标下降,这些指标的作用被弱化而造成误判。表6通过添加熵权修正了这些指标的权重,提高了故障识别率。
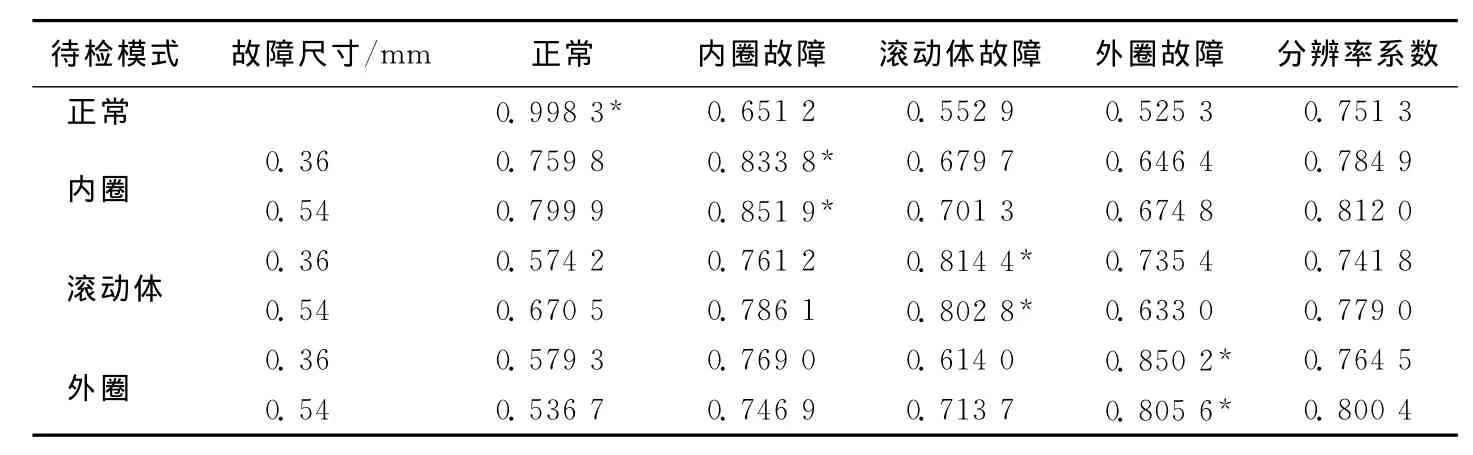
表5 待检模式与标准模式的熵权关联度
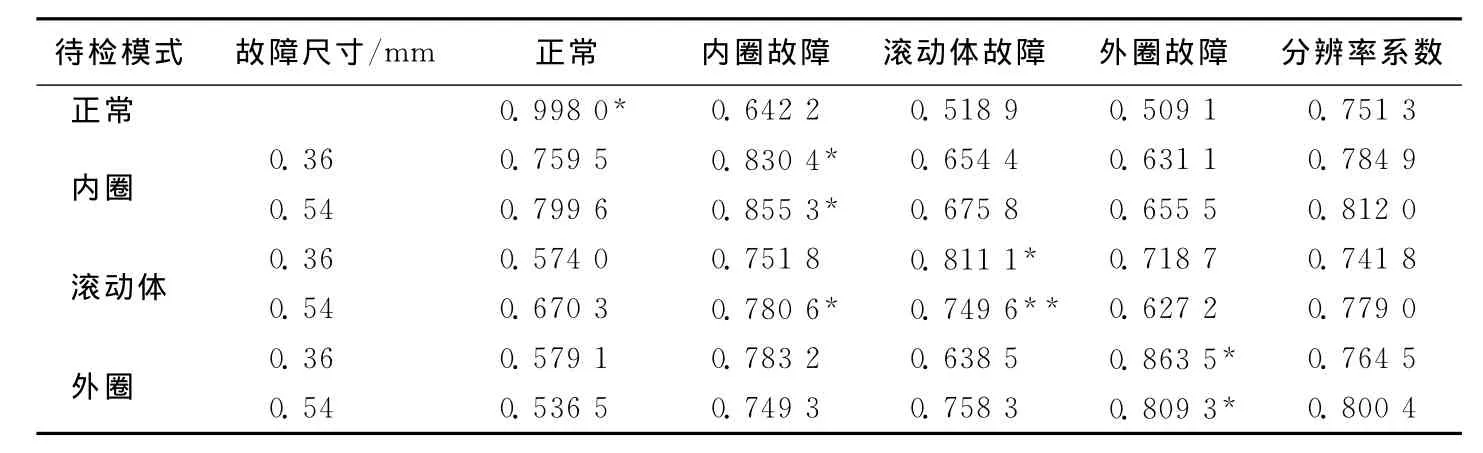
表6 待检模式与标准模式的传统A型关联度
将该方法应用到实际轴承的故障诊断中,本文选取国内某齿轮厂的70B变速器上输入轴端的一滚动轴承,制造了内圈表面剥落、滚动体表面剥落和外圈表面剥落3种故障类型,再加上正常状态,共采集这4种状态的轴承振动信号,按照灰色关联度计算方法和熵权法权重计算公式计算待检轴承与标准故障的灰色关联度,限于篇幅,本文 给出最后计算结果,见表7所列。

表7 某型号变速器轴承的灰色关联度诊断
由表7可知,该方法应用于实际轴承的故障诊断,对同种故障有较高的识别。通过对一批次轴承的噪声样本统计,该方法对正常类型的轴承有90%以上的识别率,对于各种故障类型有80%以上的识别率。
5 结束语
时频域无量纲参数可以敏感地捕捉到轴承故障出现时产生的振动信号非平稳或不规则变化信息。通过灰色关联度分析,将这些无量纲值作为评价指标,以熵权法为这些指标附加权系数提高对故障识别的灵敏度,这种方法可以简单有效地实现对轴承故障的诊断。生产现场的实际轴承故障特征需要在线不断累积,尤其是当多种故障类型并存时的相互调制,使得振动信号更为复杂,这些都对故障特征库提出更高的要求,这也是进一步工作的重点。
[1]张思扬,匡芳君,徐蔚鸿.基于WPD和模糊神经网络的轴承故障诊断[J].湖南科技大学学报:自然科学版,2010,25(2):28-31.
[2]James B.How to track rolling element bearing health with vibration signature analysis[J].Sound and Vibration,1991(11):17-22.
[3]孙 林,杨世元.基于SVM“一对一”聚类结构的滚动轴承状态诊断[J].合肥工业大学学报:自然科学版,2009,32(1):4-8.
[4]王 清.基于模糊聚类和灰色理论的齿轮箱故障诊断研究[D].太原:中北大学,2006.
[5]平 鹏,张万斌,徐泽宁.时域及功率谱特征因子诊断轴承故障的实验研究[J].振动、测试与诊断,1991,11(4):34-48.
[6]袁 幸,段志善,孙颖宏.基于EMD-AR模型和灰色关联度的滚动轴承故障诊断[J].轴承,2008(1):30-32.
[7]王 晖,陈 丽,陈 垦,等.多指标综合评价方法及权重系数的选择[J].广东药学院学报,2007,23(5):583-588.
[8]Prakash P,Yellaboina S,Ranjan A,et al.Computational prediction and experimental verification of novel IdeR binding sites in the upstream sequences of Mycobacterium tuberculosis open reading frames[J].Bioinformatics,2005,21(10):2161-2166.
[9]李国良,付 强,孙 勇,等.基于熵权的灰色关联分析模型及其应用[J].水资源与水工程学报,2006,17(6):15-18.
[10]孟浩东.基于神经网络和灰色理论的传动箱故障诊断研究[D].太原:中北大学,2005.
