基于颜色和圆形度的交通禁令标志提取

白兵乾

（河北工业大学 信息工程学院，天津 300401）

随着智能交通系统的发展，作为其重要组成部分的交通标志自动识别系统也逐渐成为研究热点。目前主要研究方向集中在识别部分，对于前期的预处理部分研究较少，而图像预处理结果直接影响识别的正确率。交通标志一般包含信息量很大，干扰较多，所以导致算法运算量较大，影响整个系统的实时性。

因此，本文提出一种基于系统实时性要求的交通禁令标志提取方法。以RGB空间代替HSI空间分割图像，以Freeman链码代替HOUGH变换求取圆形信息，避免了大量的浮点运算，提高了算法的实时性。

1 基于RGB空间的图像分割[1]

彩色图像空间最常见的是RGB空间，RGB色彩空间使用红、绿、蓝3种基色来表现彩色。三分量各自量化取值为0～255，0对应最暗，255对应最亮。在交通标志分类中，交通禁令标志以红色和黑色为主，在RGB空间中红色表示为：R=255，G=255，B=255，黑色表示为：R=0，G=0，B=0。

由它可推导出其他色彩空间，分为线性变换空间和非线性变换空间。线性变换空间有YIQ、YUV等空间。由于是有RGB空间线性变换得到，因此具有较小的计算量；典型的非线性空间有HSI、归一化RGB空间等，非线性空间能较好的消除各彩色分量的相关性，适用于图像处理。但由于变换中有大量的非线性计算过程，使得计算量巨大。

为了提高交通标志提取的速度，满足实时性要求，本文直接使用RGB彩色空间进行图像分割，这种方法不需要空间转换，减少了不必要的线性或非线性计算，极大的提高算法速度。本文通过提取交通禁令标志中的红色信息，将标志的主体轮廓提取出来。

在RGB空间中R、G、B分量易受光照影响，产生色彩失真。但通过实验发现，红色在不同光照情况下三分量的差值在一定范围内保持不变，所以通过经验选取合适的分量差阈值可将图像中的红色信息提取出来。

基于RGB空间模型的交通禁令标志分割算法如下：

对于图像中的所有点：

若满足（R－G）＞50 且（R－B）＞50，则该点为红色。

该算法结构简单，没有涉及乘法运算，极大地减少了计算量。

实验用图及分割效果如图1所示。

2 图形的边缘检测

2.1 边缘提取[2]

图像边缘是指图像中灰度变化剧烈的区域，边缘包含了图像的几何形状信息，在某些过程中对边缘的分析可取代对整幅图像的分析，这就能极大地缩短处理时间，因此对图形边缘的提取极具意义。

图像的边缘分为阶跃式和屋顶式，对于阶跃式边缘的灰度曲线其一阶导数在边缘点位置达到极大值，其二阶导数在该点处与零交叉，屋顶式边缘的特征与阶跃式正相反。这里介绍两种常用的边缘提取算子：Canny算子、log算子。

Canny算子的基本思路是首先使用高斯函数进行平滑滤波，再由灰度函数一阶微分的极大值确定边缘点。由于二阶导数的零交点即可表示极大值也可表示极小值，也就是说图像中灰度变化剧烈和缓慢的点都对应为二阶导数的零点。所以Canny算子可能引入伪边缘点。

Log算子即高斯-拉普拉斯算子，首先使用高斯函数进行平滑滤波，再由二阶的拉普拉斯算子提取边界点。拉普拉斯算子具有各向同性的特点，可以检测绝大部分边缘，并且没有出现伪边缘，可以精确定位边缘。两种算子提取边缘效果如图2所示。

本文采用log算子提取的边缘来进行处理。

2.2 图形细化

细化是图像预处理中重要的一环，其本质是在保持图形几何拓扑结构不变的前提下，尽可能地获得单像素图像骨架的过程。图像细化必须保持原图形的连通性并尽可能的获得单像素宽的边缘，细化算法速度越快越好。

细化算法种类很多，常见的有两种：查表细化法和形态学细化算法[3]。

查表细化算法的思想就是首先做出一张表，从0到255共256个元素，元素值为0或1。然后依据某点的8个相邻点的情况查表，可得到该点是否保留的信息。

形态学细化算法的细化过程就是对图像逐层剥离的过程，它利用模板对要处理的点进行邻域逻辑计算，综合判断该点是否保留。该算法能输出单像素边缘图形且不破坏原图形的连通性，具有很好的稳定性。

本文使用3×3模板的形态学细化算法进行图像的细化处理。细化效果如图3所示。

3 基于链码的圆形特征提取[4]

对于简单的直、曲线段，可用Hough变换识别形状。Hough变换是图像处理中几何形状识别的基本方法之一。

Hough变换原理是将笛卡尔坐标空间的线变换成极坐标空间中的点，从而实现了从图像空间到参数空间的映射。原始坐标系下呈现直线的所有点，它们的斜率和截距是相同的，它们在参数坐标系下对应于同一点。

Hough变换是曲线检测中较有效的方法，其优点是对于图像中噪声不敏感，其所得结果可有效滤除噪声影响。虽然常规Hough变换具有显著优势，但也有不可忽视的不足，具体表现如下：

1）当参数变为3个或3个以上时，如圆形的圆心坐标和半径，每个点映射成参数空间的一个曲面，是一到多的映射，因而计算量急剧增加。

2）Hough变换计算过程需要占用大量的内存空间，计算时间长，实时性差。

根据系统的实时性要求，本文采用基于链码计算的圆形度信息来识别目标性状。

3.1 基于链码的目标面积计算方法

Freeman码又称链码，是对图形边界点的一种编码方式，其特点是利用一系列具有固定长度和方向的直线，链接起来表示图形的边界。其表示方式为起始坐标与方向码的组合。

常用的8-方向链码定义如图4所示。

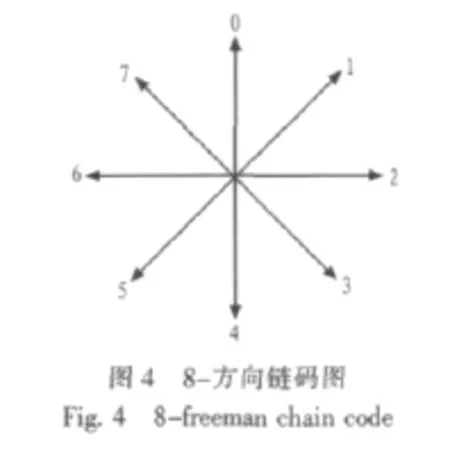
Freeman链码充分考虑了数字图像中像素的特点，将边界的变化方向编码为8个方向，大大简化了对边界的编码描述。如图5所示红点连接的边界，以边界左上角为起始点，顺时针方向寻找，其8-链码边界表示为：（3，3）222222244456666667888。

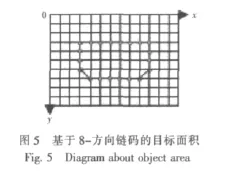
文献[5]提出了一种基于8-链码的目标面积计算方法，指出沿着8-链码轮廓对x轴积分[3]，可以得到区域的面积。

以图5中边界所围区域为例，其面积即用图6中灰色部分减去黑色部分得到目标区域面积，计算公式如下：

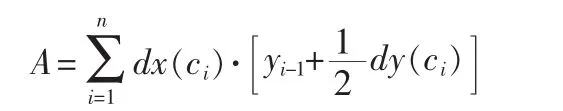
式中，yi=yi-1+dy（ci），y0；是初始点坐标；dx（ci）和 dy（ci）分别表示横坐标和纵坐标相对上一位置的偏移量。

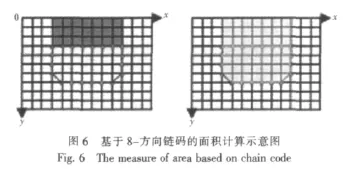
图5中目标所围区域面积为27。该方法忽略了边界部分的大小，当所求面积较小时，误差会很大，所以目标区域面积实际值应为所求值加上边界点个数。

3.2 圆形特征提取

在形状分析中，圆形度是图形几何特征中较常用的一种特征之一，其通常定义如下：

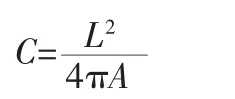
其中，L为目标的周长，A为目标的面积。

圆形度，C表示图形与圆形的接近程度，C越接近于1，形状越接近于圆形。

获取目标区域的链码以后，可根据链码直接计算目标图形的周长。常规方法为将目标周长表示为链码个数之和。

当获取目标的面积和周长后，就可以计算圆形度。当目标区域为圆形时，圆形度为1，圆形度越远离1，说明目标区域的形状越复杂。

4 圆形目标提取算法实现

该算法计算图像中闭合区域的圆形度，若圆形度在区间[0.75，1]内，则认定该区域为圆形区域，输出该区域的坐标范围，并显示提取后的图像，提取结果如图7所示。

算法基本思路是：以图像左上角为初始点历遍整个图像，遇到非零点后按8-方向链码0-8的方向依次寻找相邻点，若各相邻点连接为闭合图形，即按搜寻方向可回到初始点。则计算该图形面积及圆形度，并与所设阈值比较，若满足条件，则认定为圆形区域。保存整个闭合圆形的横纵坐标的极值，并输出提取到圆形区域。算法流程如下：

1）初始化。将横、纵坐标极大值、极小值、面积、周长、圆形度的初始值设置为0，按照从上到下，从左至右的顺序依次扫描图象。若遇到非零点则保存初始点坐标并转到第2步，若到达图象右下坐标，则转到第4步。

2）按顺时针方向搜寻相邻点，若没有相邻点或达到图象右下坐标则跳转到第4步，若有则依照面积计算公式更新面积值，周长自加1，比较该点坐标及横纵坐标极值并更新极值，跳转到第3步。

3）判断是否回到初始点，是则跳转第4步，否则将目标点值零（变为背景色），跳转第2步继续执行。

4）若程序在初始点位置且周长大于2，则计算目标圆形度，否则圆形度值零。若圆形度满足[0.75，1]输出横、纵坐标极值坐标，并显示提取到的目标图形，退出程序。

当圆形目标畸变过大时，本方法将无法正确提取目标。取样本20个，所得的实验结果如表1所示。

表1 实验结果Tab.1 Result of experiment

5 结论

基于圆形度的目标形状分析是形状分析中的重要内容，可应用于计算机视觉、工业自动化、智能导航系统等领域。本文提出的交通禁令标志提取算法，处理速度快，检测效果好，能够满足系统实时性和有效性的要求，可应用于智能交通网络及智能汽车系统，应用前景较为广泛。

[1]黄志勇，孙光民，李芳.基于RGB视觉模型的交通标志分割[J].微电子学与计算机，2004，21（10）：147-148.HUANG Zhi-yong， SUN Guang-min， LI Fang.Traffic sign segment based on RGB vision model[J].Microelectronics&Computer， 2004， 21（10）：147-148.

[2]段瑞玲，李庆祥，李玉和.图像边缘检测方法研究综述[J].光学技术，2005，31（3）：415-419.DUAN Rui-ling， LI Qing-xiang， LI Yu-he.Summary of image edge detection[J].Optical Technique， 2005， 31（3）：415-419.

[3]李迎，段汕.基于数学形态学的二值图像细化算法研究[J].中南民族大学学报，2005，24（4）：96-99.LI Ying，DUAN Shan.Study of binary image thinning based on mathematicalmorphology[J].JournalofSouth-Central Univercity for National-Ities， 2005， 24（4）：96-99.

[4]韩殿元.基于链码的圆形目标分析 [J].潍坊学院学报，2008，8（2）：29-31.HAN Dian-yuan.An analysis on circle object based on chain code[J].Journal of Weifang University， 2008， 8（2）：29-31.

[5]杨万扣，任明武，杨静宇.数字图像中基于链码的目标面积计算方法[J].计算机工程，2008，34（1）：30-33.YANG Wang-kou， REN Ming-wu， YANG Jing-yu.Object area algorithms based on chain code in digital image[J].Computer Engineering， 2008， 34（1）：30-33.

[6]陆宗骐，童韬.链码和在边界形状分析中的应用[J].中国图象图形学报，2002，7（12）：1323-1328.LU Zong-qi，TONG Tao.The application of chain code sum in the edge form analysis[J].Journal of Image and Graphics，2002， 7（12）：1323-1328.