大跨多塔悬索桥纵向地震碰撞反应参数研究

邓育林，彭天波，李建中

(1.武汉理工大学 交通学院，武汉 430063;2.同济大学 桥梁工程系，上海 200092)

最近30余年，地球上发生的多次地震灾害对桥梁抗震设计理论产生了巨大的影响。美国、日本等国，对于传统的抗震设计、分析方法有了重新的认识，并且开展了一系列深入的研究。其中在地震作用下，相邻桥跨的非同向运动及碰撞问题被认为是影响结构地震反应和抗震性能的一个重要因素。许多桥梁结构的地震震害表明:相邻桥跨的非同向运动及碰撞是引起结构破坏的主要原因。

目前，国内外有很多学者针对地震作用下连续梁桥碰撞效应进行过研究(Malhotra［1］、Hong［2］、Jankowski［3，4］、Kawashima［5，6］、王军文［7，8］等)，研究表明:相邻桥跨的周期比、伸缩缝间隙大小、质量比以及墩柱的弹塑性等对连续梁桥地震碰撞反应都有影响，其中相邻桥跨的周期比被认为是影响连续梁桥地震碰撞反应的主要因素，而且相邻联的振动周期相差越大，碰撞效应越明显。而对大跨桥梁主、引桥伸缩缝处相邻梁体的碰撞效应研究很少。为揭示大跨桥梁主、引桥伸缩缝处相邻梁体的碰撞对桥梁结构地震反应的影响规律，本文以一座大跨三塔悬索桥为工程背景，建立复杂的空间非线性碰撞计算模型，研究碰撞刚度、碰撞初始间隙等因素对碰撞效应的影响，探讨各个参数对碰撞效应的影响规律。

1 计算模型

泰州长江公路大桥为一座大跨度三塔悬索桥，总体布置图见图1所示，两个主跨跨度均为1080 m，主缆的分跨为390 m+1080 m+1080 m+390 m，桥面设6车道，主缆在设计成桥状态矢跨比为1/9，两根主缆横向间距为35.8 m，加劲梁采用封闭式流线型扁平钢箱梁。边塔为混凝土塔，索塔总高178.0 m;中塔为变截面钢塔，索塔总高192.0 m，横桥向为门式框架结构，纵向为人字型。中塔下横梁上不设竖向支座，也不设0号吊索，在索塔内侧壁与加劲梁间安装横向抗风支座，纵向设弹性索;在边塔下横梁上设置竖向和侧向支座。边塔采用46根D3.1/D2.8 m变截面钻孔桩群桩基础，中塔采用倒圆角的矩形沉井基础。

图1 三塔悬索桥布置图Fig.1 Aarrangement of triple-tower suspension bridge

大跨桥梁的引桥一般为多联多跨连续梁桥，单跨跨径大多在50 m～100 m之间，且一般为混凝土结构。本文分析时只考虑北侧单边碰撞效应，为具代表性，北引桥取为4 m×70 m连续梁桥，中间墩为固定墩，其余为活动墩，墩高从20 m～50 m变化，墩身为等截面，外围尺寸为6.5 m×4.2 m，纵筋配筋率取2%。

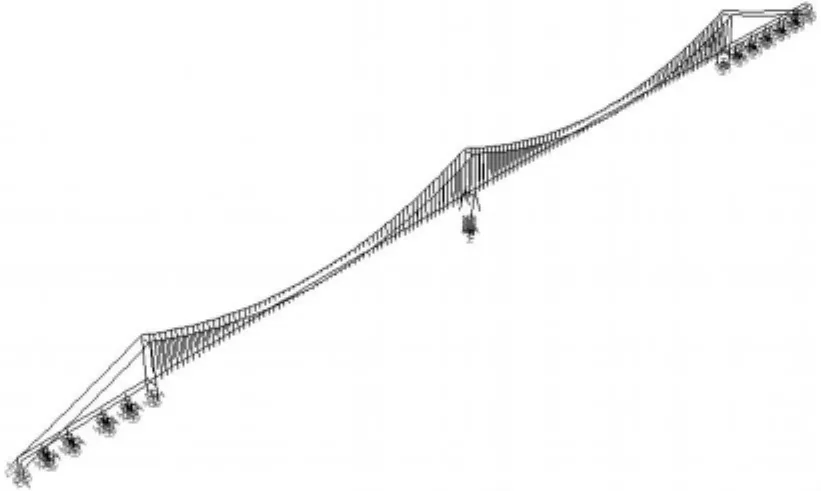
图2 动力计算模型Fig.2 Dynamic analysis model

三维有限元模型如图2所示，利用空间梁单元模拟主梁、主塔和墩柱，用空间杆单元模拟主缆、吊杆;主缆、主塔和吊杆均考虑恒载引起的几何刚度的影响。对于边塔，由于一般冲刷层位尚在承台底面以上，属于低桩承台基础，采用在承台底中心加6×6的土弹簧来模拟桩土相互作用，而对于中塔，不考虑沉井－土相互作用，在一般冲刷线处将沉井固结。

为模拟伸缩缝处主、引桥相邻梁体的碰撞效应，在伸缩缝处添加接触碰撞单元，如图3所示(引桥一般为双幅并联)。

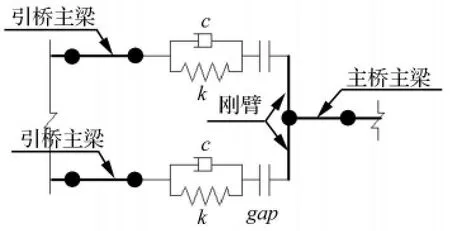
图3 接触碰撞单元Fig.3 Pounding element model

接触碰撞单元采用 Kelvin碰撞模型［9，10］由一个刚度为kk的线性弹簧与阻尼器(ck)并联来模拟相邻刚体之间的碰撞，在碰撞期间的接触力如下:

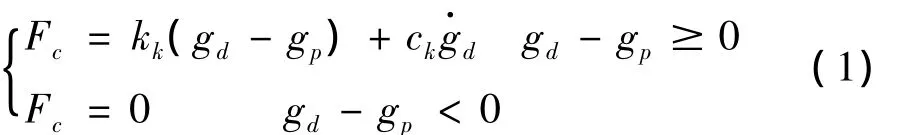
式中，gp为伸缩缝初始间隙，gd为地震作用下伸缩缝处相邻梁体的相对位移，kk为接触刚度，取碰撞较短梁体的轴向刚度。

碰撞过程中的能量损失采用阻尼比表示，阻尼的大小与碰撞过程的恢复系数e有关，根据能量守恒定律，可以建立阻尼系数ck与恢复系数e之间的关系如下:

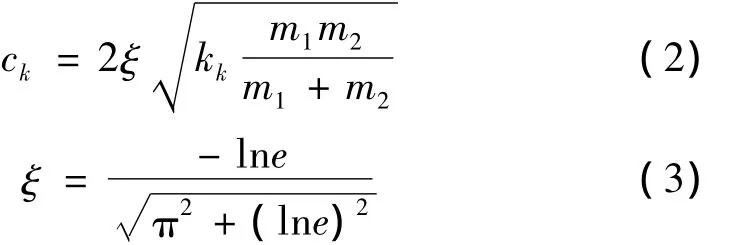
式中，m1和m2分别为两碰撞刚体的质量。

2 地震动输入

由于地震动的随机性，本文分析时根据不同的地震动参数(特征周期)选取表1所示的9条地震波，并将加速度峰值调整到0.4 g，沿结构纵向输入。所选地震波的特征周期覆盖范围较大，在0.26 s～0.88 s之间变化，这样分析结果具有一定的普遍性和代表性。

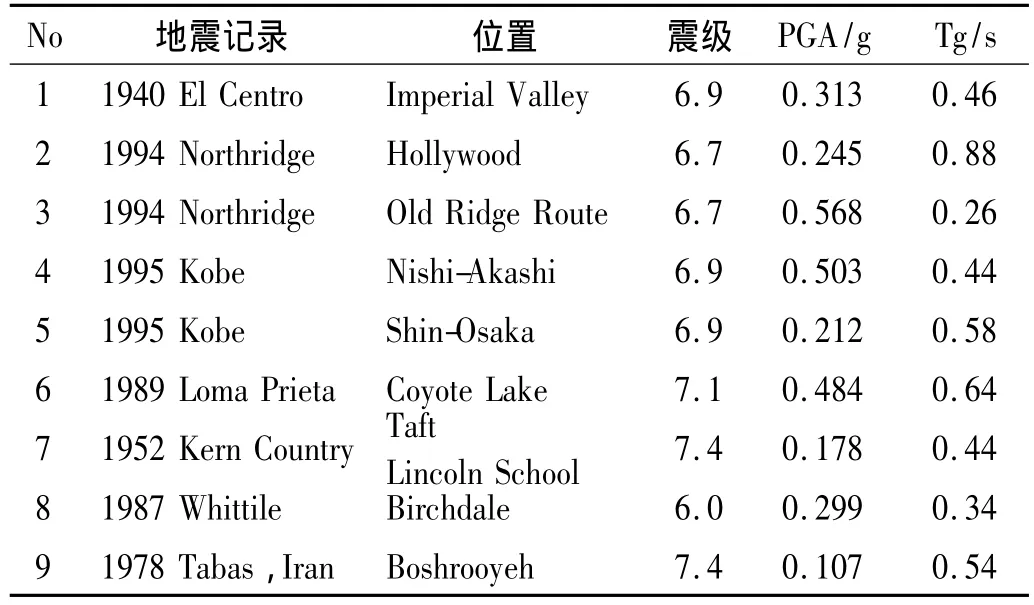
表1 选取的地震波Tab.1 Selected free-field ground motions

3 主引桥动力特性比较

伸缩缝处相对位移的大小与两端结构的振型周期有关，对于引桥，其梁端位移主要由纵桥向第一阶振型贡献;而对于主桥，分析表明，其梁端位移也是由某一阶振型起主要贡献，该阶振型周期的大小和中塔与主梁之间的弹性索刚度有关。

表2列出了不同墩高引桥第一阶振型周期，记为T1;表3列出了主桥梁端位移控制振型周期(以下简称周期)，记为T0。从表2、表3可以看出，当引桥墩高为35 m时，主、引桥梁端位移控制振型的周期比较接近。

表2 引桥周期(桥墩保持弹性)Tab.2 Period ofapproach span(piers keep in el－ asticity)

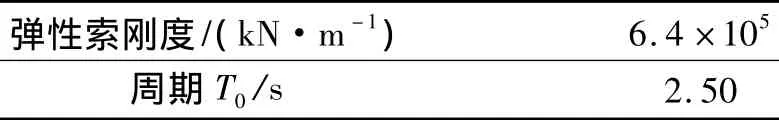
表3 主桥周期Tab.3 Period of main span

由于在强震作用下，引桥固定墩有可能屈服，而主桥主体结构要求基本保持弹性，因此，分析强震作用下主、引桥相对位移的变化规律，引桥考虑两种情况:一假定桥墩保持弹性，二考虑桥墩弹塑性的影响。

有限元模型的模拟采用美国加州大学伯克利分校开发的有限元分析软件OpenSees［11］来实现，其中桥墩分别采用弹性梁单元或Fiber梁单元［12－15］模拟。输入表1中9条地震波，地震波峰值加速度统一调到0.4 g，不考虑碰撞效应。

图4给出了两种情形下，主、引桥间相对位移的随引桥墩高的变化曲线，取9条波的均值加1倍标准差。从图4及表2、表3可以看出:当中塔与主梁之间设置弹性索时，对于模型Ⅰ，引桥墩高为35 m时T1与T0最接近，伸缩缝处主、引桥相对位移达到最小;考虑桥墩弹塑性的影响后，由于桥墩屈服，刚度下降，伸缩缝处主、引桥相对位移在引桥墩高25 m时达到最小。为后面叙述方便，将引桥弹塑性体系等效成周期为Teq的弹性体系，使得主、引桥相对位移最大值相等。对于模型Ⅱ，引桥墩高为25 m时Teq与T0最为接近。

4 参数影响分析

由于碰撞问题非常复杂，其影响因素较多。相邻桥跨的周期比、伸缩缝间隙大小、质量比以及碰撞单元刚度的取值对碰撞反应都有影响，其中相邻桥跨的周期比被认为是影响地震碰撞反应的主要因素，而且相邻联的振动周期相差越大，碰撞效应越明显。限于篇幅，本文不考虑地震动的空间效应，主要研究一致激励下碰撞刚度、伸缩缝间隙对不同墩高引桥地震反应的影响，分析时为考虑在强震作用下，引桥固定墩有可能屈服，采用Fiber梁单元模拟桥墩，即上节的模型Ⅱ。

4.1 碰撞刚度的影响

研究碰撞效应时，碰撞刚度是一个非常重要的参数，许多学者［3，7］研究表明，碰撞效应与碰撞刚度的选取大小非常敏感，一般认为，随着碰撞刚度取值越大，不仅计算得到的局部碰撞力越大，而且结构的地震需求也越大。

由于碰撞问题的高度复杂性，精确确定碰撞刚度的大小是非常困难，有时也是不必要的。目前大多数学者都建议碰撞刚度值应与碰撞梁体轴向刚度为同一数量级，其中王东升等［16，17］利用基于直杆共轴碰撞理论的碰撞分析模型，采用解析解与数值解结合的方法研究发现碰撞弹簧刚度约为0.5倍较短主梁轴向刚度。根据王东升等研究结果，本次分析模型的碰撞刚度为6.5×105kN/m。但碰撞刚度也不宜取值太小，避免相邻梁体过多的重叠。为进一步探明碰撞刚度选取大小对碰撞效应的影响，下面对碰撞刚度进行参数分析，刚度选取范围为1.0×105kN/m ～2.0×107kN/m，共分1.0×105kN/m、2.5×105kN/m、5.0×105kN/m、1.0 ×106kN/m、2.5 ×106kN/m、5.0 ×106kN/m、1.0 ×107kN/m、2.0 ×107kN/m 八个等级。

图4 主、引桥相对位移Fig.4 Relative displacement between main span and approach span

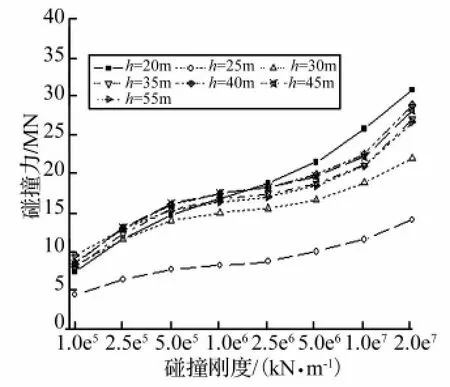
图5 碰撞力峰值Fig.5 Peak pounding force

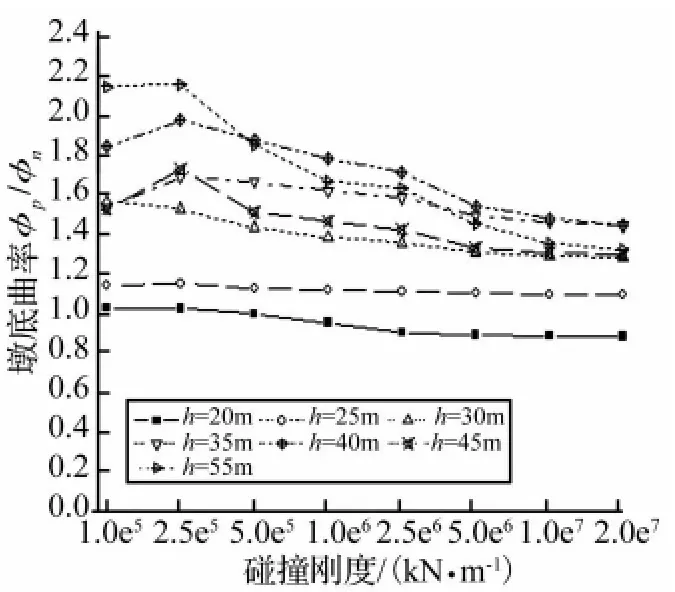
图6 墩底曲率峰值比Fig.6 Amplification of peak curvature of pier

图5分别给出了碰撞力峰值随碰撞刚度大小的变化曲线，取9条波的平均值。从图5可以看出:碰撞力峰值随碰撞刚度的增大均单调上升，但当碰撞刚度在5.0×105kN/m ～5.0 ×106kN/m 范围变化时，碰撞力峰值增大并不显著;对于中塔与主梁之间设置纵向弹性索，碰撞刚度分别取5.0 ×105kN/m、1.0 ×106kN/m和5.0×106kN/m时分析得到的碰撞力峰值分别比碰撞刚度取2.5×106kN/m时平均大(或小)12.8%、4.1%和9.9%。从以上比较数据可以看出，在碰撞刚度可能范围内取值，分析得到的碰撞力峰值相差并不大。

图6给出了引桥墩底曲率(φp/φn)需求峰值比随碰撞刚度大小的变化曲线，取9条波的平均值，其中下标p和n分别表示考虑碰撞效应和不考虑碰撞效应时的反应。特别指出，本文出现的引桥墩底曲率均指固定墩墩底曲率。

从图6可以看出，当碰撞刚度在1.0×105kN/m～2.5×106kN/m范围内变化时，引桥墩底曲率需求会产生小幅变化，并且随着引桥墩高的增大，变化幅度越大;而当碰撞刚度大于2.5×106kN/m后，碰撞刚度的变化对引桥的墩底曲率需求影响甚微。

图7～图9分别给出了主桥梁端位移、引桥梁端位移(Dp/Dn)以及主引桥间相对位移(ΔDp/ΔDn)需求峰值比随碰撞刚度大小的变化曲线，取9条波的平均值，其中下标p和n分别表示考虑碰撞效应和不考虑碰撞效应时的反应。

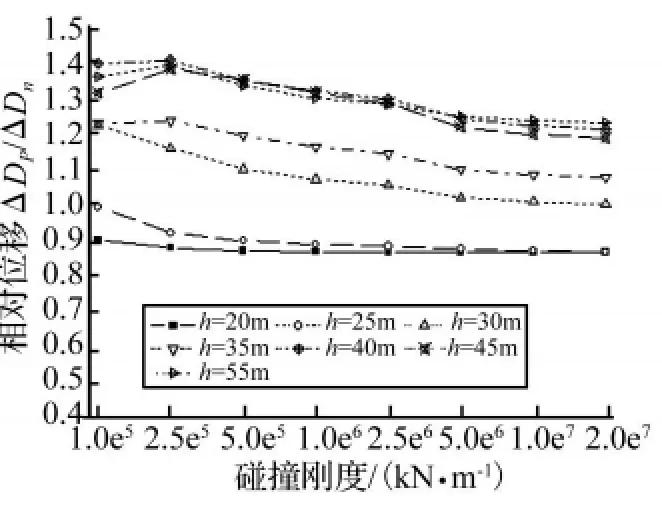
图7 主引桥相对位移峰值比Fig.7 Amplification of peak relative displacement

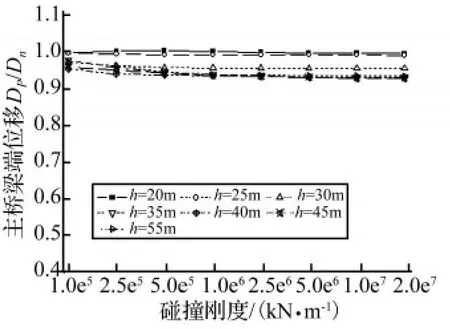
图8 主桥梁端位移峰值比Fig.8 Amplification of peak displacement of main girder

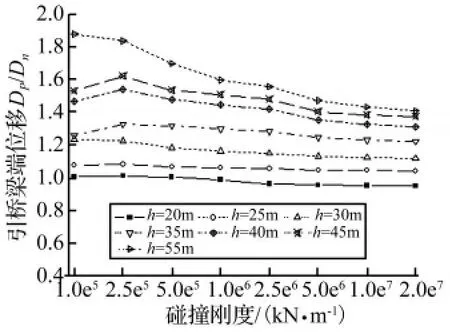
图9 引桥梁端位移峰值比Fig.9 Amplification of peak displacement of approach beam

从图7～图9可以看出:碰撞刚度的变化对引桥梁端位移以及主、引桥间相对位移需求有一定影响，但对主桥梁端位移影响甚微;当碰撞刚度在1.0×105kN/m～5.0×106kN/m范围内变化时，引桥梁端位移以及主、引桥间相对位移变化略大，并且当引桥墩高较高时，变化幅度较明显，当碰撞刚度大于5.0×106kN/m后，碰撞刚度的变化对引桥梁端位移以及主、引桥间相对位移需求的影响不大。

从以上分析可以看出，碰撞刚度在一定范围内取值，碰撞效应的变化并不明显，特别是当碰撞刚度取值大于2.5×106kN/m后，碰撞效应对主、引桥的影响很小，因此，对于本桥碰撞刚度可取为5×106kN/m左右。

4.2 碰撞间隙的影响

为了分析伸缩缝间隙对碰撞效应的影响，本文引入一个无量纲参数—间隙比rG，rG由下式定义:

其中Δmax为不考虑碰撞时伸缩缝处两相邻梁体的最大相对位移。如果 rG＞1.0，不发生碰撞;如果 rG＜1.0，将发生碰撞。

在分析间隙比对碰撞效应的影响时，输入表1的9条地震波，对间隙比 rG=0.1，0.2，…，0.9 时结构的地震反应分别进行计算，碰撞刚度取值为5×106kN/m。

图10给出了碰撞力峰值随初始间隙比大小的变化曲线，取9条波的平均值。从图10可以看出，不管引桥墩高多少，碰撞力峰值随初始间隙比的增大均单调减小;当初始间隙比rG＜0.5，碰撞力峰值下降速度略缓，而当初始间隙比rG＞0.5后，碰撞力峰值下降略快。

图11给出了引桥墩底曲率(φp/φn)需求峰值比随初始间隙比大小的变化曲线，取9条波的平均值，其中下标p和n分别表示考虑碰撞效应和不考虑碰撞效应时的反应。

从图11可以看出:当主桥T0大于引桥Teq(引桥墩高为20 m)时，引桥墩底曲率(φp/φn)需求峰值比随初始间隙比的增大而略有增大，且趋向于1，即碰撞对引桥的影响随初始间隙比的增大而减小;当主桥T0小于引桥 Teq(引桥墩高大于 25 m)时，引桥墩底曲率(φp/φn)需求峰值比总体上随初始间隙比的增大而减小，且同样趋向于1，即碰撞对引桥墩底曲率随初始间隙比的增大而减小。

图12～图14分别给出了主桥梁端位移、引桥梁端位移(Dp/Dn)以及主引桥相对位移(ΔDp/ΔDn)需求峰值比随初始间隙比大小的变化曲线，取9条波的平均值，其中下标p和n分别表示考虑碰撞效应和不考虑碰撞效应时的反应。

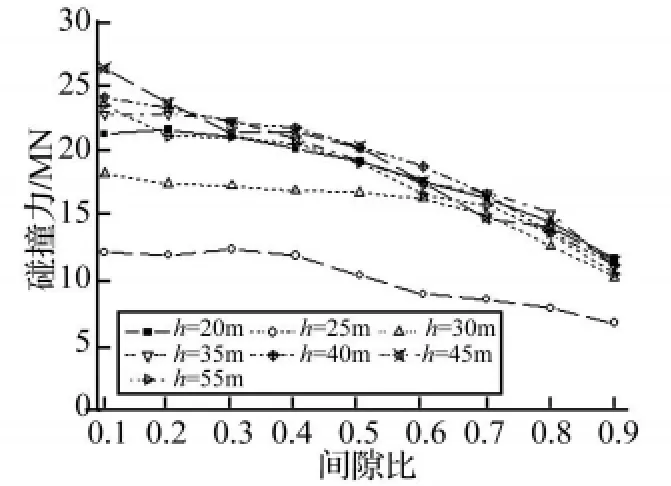
图10 碰撞力峰值Fig.10 Peak pounding force

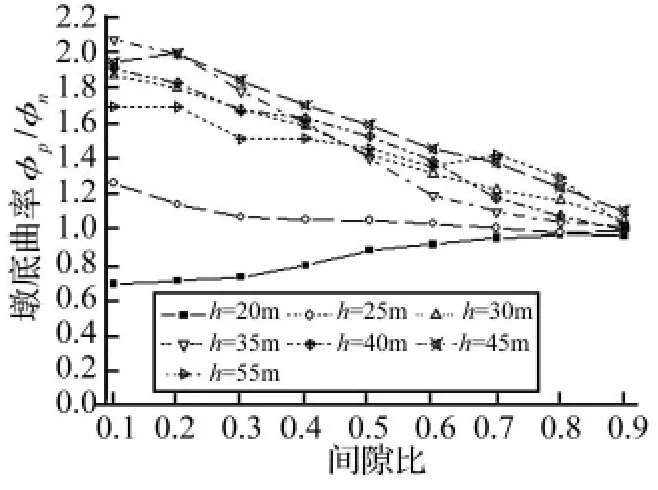
图11 墩底曲率峰值比Fig.11 Amplification of peak curvature of pier

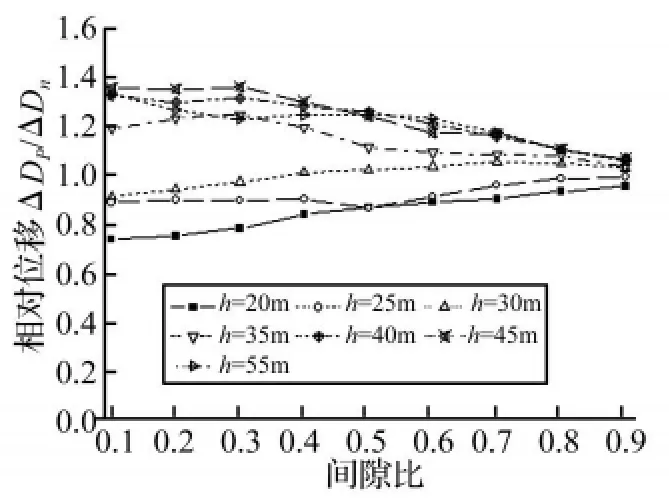
图12 主引桥相对位移峰值比Fig.12 Amplification of peak relative displacement

从图12～图14可以看出:当主桥T0与引桥Teq(引桥墩高为20 m～30 m)接近时，主引桥相对位移需求峰值比(ΔDp/ΔDn)随初始间隙比的增大而增大，而当引桥Teq大于主桥T0(引桥墩高大于30 m)时，主引桥相对位移需求峰值比(ΔDp/ΔDn)随初始间隙比的增大而减小，但两者变化均趋向于1，即碰撞对主引桥相对位移的影响随初始间隙比的增大而减小;当主桥T0与引桥Teq(引桥墩高为20 m～30 m)接近时，初始间隙比的变化对主桥梁端位移影响很小，而当引桥Teq大于主桥T0(引桥墩高大于30 m)时，主桥梁端位移需求峰值比(Dp/Dn)随初始间隙比的增大而增大，且趋向于1，即碰撞对主桥梁端位移的影响随初始间隙比的增大而减小;当主桥T0大于引桥Teq(引桥墩高为20 m)时，初始间隙比的变化对引桥梁端位移影响很小，而当引桥Teq大于主桥T0(引桥墩高大于25 m)时，引桥梁端位移需求峰值比(Dp/Dn)随初始间隙比的增大而减小，且随着引桥墩高的增大下降更为明显。

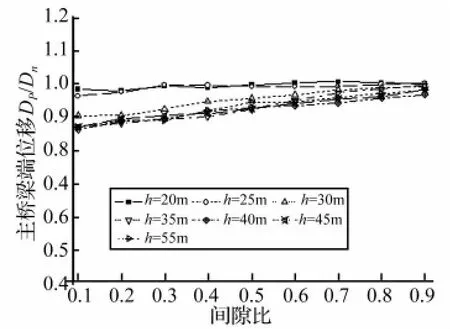
图13 主桥梁端位移峰值比Fig.13 Amplification of peak displacement of main girder

从以上分析可以看出，对于本次分析模型，碰撞初始间隙是一个敏感参数，其大小对于碰撞效应有一定的影响，特别是对引桥位移以及主引桥相对位移影响比较显著。尽管如此，碰撞初始间隙的变化并不会从根本上改变碰撞效应的影响趋势。

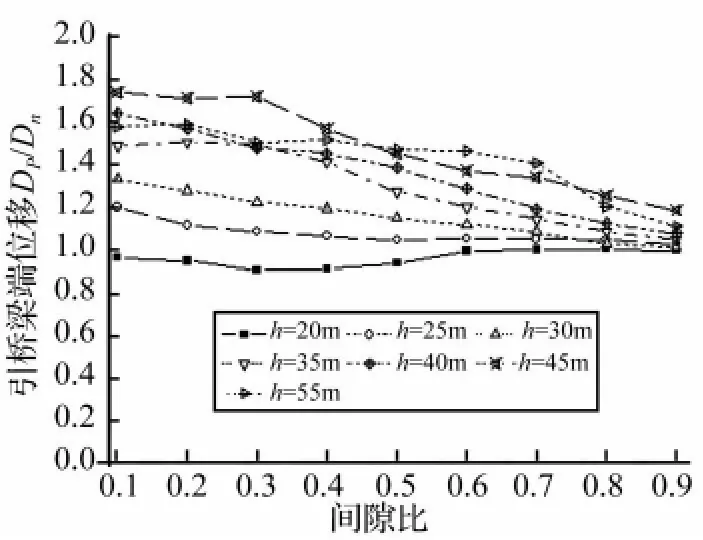
图14 引桥梁端位移峰值比Fig.14 Amplification of peak displacement of approach beam

5 结论

本文以一座大跨三塔悬索桥为工程背景，建立了复杂的空间非线性碰撞计算模型，详细分析了碰撞刚度、碰撞初始间隙等因素对碰撞效应的影响，得出了各个参数对碰撞效应的影响规律。通过分析可以得出以下结论:

(1) 就本桥而言，碰撞力峰值随碰撞刚度的增大单调上升，但当碰撞刚度在5.0×105kN/m～5.0×106kN/m范围变化时，碰撞力峰值增大比较平缓;

(2)就本桥而言，当碰撞刚度取值大于2.5×106kN/m后，碰撞效应对主、引桥地震需求的影响很小，对引桥梁端位移以及主引桥相对位移需求的影响也不大。

(3)就本桥而言，碰撞初始间隙对于碰撞效应有一定的影响，特别是对引桥位移以及主引桥相对位移影响比较显著;总体上碰撞效应随初始间隙比的增大而减小。

［1］Malhotra P K.Dynamics of seismic pounding at expansion joints of concrete bridges［J］.Journal of Engineering Mechanics/July，1998:794 －802.

［2］Chouw N，Hao H.Study of SSI and non-uniform ground motion effect on pounding between bridge girders［J］.Soil Dynamics and Earthquake Engineering， 2005， 25:717－728.

［3］Jankowski R，Wilde K，Fujino Y.Reduction of pounding effects in elevated bridges during earthquakes ［J］.Earthquake Engineering and Structural Dynamics.2000，29:195－212.

［4］Jankowski R，Wilde K，Fujino Y.Pounding of superstructure segments in isolated elevated bridge during earthquakes［J］.Earthquake Engineering and Structural Dynamics.1998，27:487－502.

［5］Ruangrassamee A，KawashimaK.Relativedisplacement response spectra with pounding effect.12wcee(2000)，paper No.1957.

［6］Ruangrassamee A， Kawashima K. Relative displacement response spectra with pounding effect［J］.Earthquake Engineering and Structural Dynamics，2001，30:1511 －1538.

［7］王军文，李建中，范立础.非规则梁桥伸缩缝处的碰撞对地震反应的影响［J］.土木工程学报，2006，30(1):54－59.

［8］王军文，李建中，范立础.连续梁桥纵向地震碰撞反应参数研究［J］.中国公路学报，2005，18(4):42－47.

［9］Maison B F，kasai K.Analysis for type of structural pounding［J］.J.Struct.Eng.ASCE，1990，116(4):957 －977.

［10］Muthukumar S.A contact element approach with hysteresisdamping for the analysis and design of pounding in bridges［D］.2003，11.

［11］OpenSeesCommand Language Manual［M］. Pacific EarthquakeEngineering Research Center，University of California，Berkeley，OpenSees version 1.7.3.2007.

［12］Taucer F F，Enrico S.Fiber beam-column model for seismic response analysis of reinforced concrete structures［R］.EERC 91－17，1991.

［13］Kent D C，Park R.Flexural members with confined concrete［J］.Journal of The Structural Division，ASCE，1971，97(7):1969－1990.

［14］Filippou.A simple model for reinforcing bar anchorages under cyclic excitations［J］.Journal of The Structural Division，ASCE，1986，112(7):1639 －1659.

［15］Menegotto M，Pinto P E.Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending［C］.Proceedings，IABSE Symposium on Resistance and Ultimate Deformability of Structures，Lisbon，1973.15 －22.

［16］王东升，冯启民，王国新.基于直杆共轴碰撞理论的桥梁地震反应邻梁碰撞分析模型［J］.工程力学，2004，21(2):157－166.

［17］王东升，王国新，冯启民.桥梁结构地震反应邻梁碰撞分析等效刚体模型［J］.工程力学，2004，21(8):81－85.