一种多体系统冲击响应谱分析法
2011-06-05贺少华吴新跃
贺少华,吴新跃
(海军工程大学 船舶与动力学院,武汉 430033)
对于结构动力学,当然也包括运动学,响应特性的获得一般分为三个步骤,首先建立实际对象的数学模型由于实际对象理所当然是一个连续系统,所以对于简单结构对象,我们可以直接以偏微分方程的形式建立连续系统数学方程,但是我们对这种方程的求解能力十分有限,一般仅限于弦、杆、轴、梁等简单结构。当对象结构变得复杂时,我们必须采用另外一种建模方法,那就是将连续系统离散化,即建立连续系统的“近似”—离散系统。目前建立离散系统的方法有很多,如我们熟悉的集中质量法、有限元方法、多体系统法等。建立完实际对象的抽象数学模型,之后就是要建立模型在特定物理环境中的动力学方程,目前动力学方程的建立主要基于两大力学理论——矢量力学和分析力学,基于这两大理论,出现了一大批风格各异各有所长的动力学方程建立方法,如牛顿-欧拉方程法、拉格朗日方程法、变分方法、凯恩方法、旋量方法、传递矩阵方法等,其中的很多方法是随着计算机技术的发展而建立的,其共同目标是要实现一种高度程式化,适应编制计算程序的动力学方程建立方法。最后,得到物理模型的动力学方程后,就是对这些方程的求解,从而得到动力学响应特性。对于线性系统方程而言,我们可以采用解析方法、模态叠加法等,对于非线性方程而言,我们则可以采用近似解析方法和数值积分方法,近似解析方法主要针对弱非线性系统的稳态响应的求解,如摄动法、谐波平衡法、多尺度方法、平均法等,而数值积分方法如显式算法中的中心差分法、Runge_Kutta法和隐式算法中的 Wilson-θ法、Houbolt法、Newmark法等,它们则适合强非线性问题的求解[1-4]。当然,上面的这些方法有些并没有严格的界限,有些方法的本质是一致的。另外,还有许多方法是在这些方法基础之上或者联合几种方法建立来的,在这就不一一列举。
舰用机械设备冲击响应仿真建模与计算是随着计算机软硬件水平和力学、计算数学等学科知识的发展而发展起来的,几十年来,已出现了数十种方法,均体现了当时相应各学科的发展水平,总的来说,这些方法均有特定适应的对象,各有优缺点,针对不同的分析对象必须采用不同的计算分析方法。显然,评价一个力学模型优劣的重要标准应该是该模型是否能够可靠和高速处理各种动力学现象,通常解的精确和计算所要付出的代价是一对矛盾。对于舰用设备特别是复杂动力机械设备,通常采用有限元法、有限元子结构法、多体系统法、集总质量法进行离散化建模。而冲击动力学方程的建立则主要采用经典矢量力学的方法,方程响应的求解则主要采用模态叠加法、数值积分法。针对线性系统,主要采用基于模态叠加原理的谱分析法[5-7],如著名的 DDAM 法就是其中的一种;针对非线性系统,则主要出现了增量模态叠加法、伪力法和几种数值积分方法[8,9]。
随着有限元和计算机技术水平的飞速发展,目前借助商业化的有限元软件进行舰用机械设备的冲击响应计算分析成为了国内的主流。但是,必须指出的是,绝大部分有限元商业软件的知识产权属于国外,过分依赖这些商业软件将使我国本已滞后的舰船及设备抗冲研究特别是理论研究更加落后于国外。实际上,在上面文字中已经提到,除有限元方法外,另外一种建模和计算方法即多体系统法在舰用复杂机械冲击动力学研究上更具应用潜质,因为该方法相对有限元法具有更加节省计算资源和易于理论创新的优势。近几年来,国内相关学者开始将多体系统动力学方法运用到舰船及设备抗冲研究上面。我们知道,目前的冲击响应谱分析方法一般采用的还是有限元建模,而本文的目的就是要建立一种基于多体系统建模方法的冲击响应谱分析方法。
1 方法理论基础
我们知道,冲击响应谱分析方法的基础是模态叠加理论,系统特征矢量(特征函数)的正交性是系统动力响应可以用有限几阶模态就可快速收敛到所需工程精度要求的前提条件,但是,由于多体系统中刚体与弹性体之间的动力耦合作用,使得多刚柔系统的特征值问题非自共轭,振型函数不具有通常意义下的正交性,难以用模态方法精确分析系统的动力响应。为解决多刚柔系统特征矢量正交性,文献[10,11]引入了多体系统增广特征矢量和增广算子的概念,通过建立满足对称性的增广公式,证明了增广特征矢量自动满足正交性,为实现多刚柔系统动力响应的精确分析创造了条件,也为本文的多体系统冲击响应谱分析法的创立提供了可能性。增广特征矢量同时含有体元件线位移和角位移的模态坐标,但又不是两者的简单结合,同时含有离散变量和连续变量,它的变量个数等于系统体动力学方程的个数,这些都是增广特征矢量不同于一般特征矢量的特点。增广特征矢量的构造过程简单而程式化,只需按序列写出描述体元件运动状态的位移参量即可得到增广特征矢量。
下面我们以一个基础受冲击简单多刚柔系统为例来阐述本文提出的多体系统冲击响应谱分析法的一般原理。
如图1所示平面振动刚柔系统,由弹性系数为k的弹簧1、质量为m的集中质量(刚体)2和长度为l、线质量密度为、抗弯刚度为EI等截面Euler-Bernoulli梁3组成。集中质量2受光滑导槽的约束做往复运动,梁3左端与刚体2固接于点Q,右端自由。初始时刻梁3未变形,基础的y向加速度冲击激励时间历程为ü,无外力和阻尼作用,求系统任意点冲击响应时间历程。
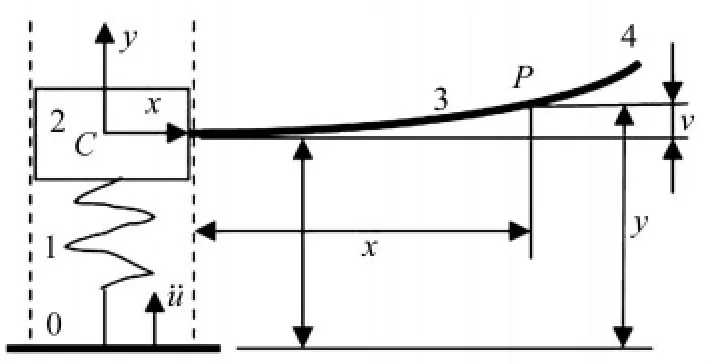
图1 由弹簧、集中质量和梁组成的刚柔混合系统Fig.1 A multi-rigid-f lexible-body system composed of spring,centralized mass and beam
有限元法是结构分析中应用最广泛和强有力的工具,但对复杂结构使用大量节点导致必须处理和管理非常大的矩阵,计算工作量大,大刚度梯度系统往往伴随计算“病态”,导致计算困难,而多体系统结合传递矩阵法就能较好地克服这一问题。
以弹簧1与地面(基础)0的联结点为输入端,梁的自由端 4 为输出端,定义状态矢量 Z0,Z1,2,Z2,3,Zx(0 < x≤l)为 Z=[Y,Θz,Mz,Qy]T,其中 Y,Θz,Mz,Qy分别为沿y轴向的位移,绕z轴的角位移,z向力矩和y向剪切力。各个元件的传递方程为:
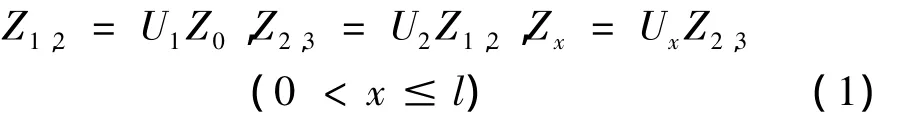
各个元件的传递矩阵为:
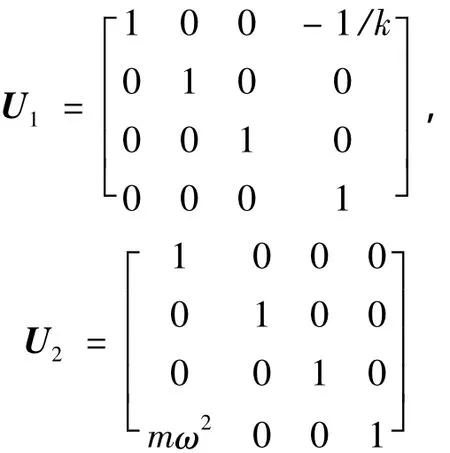
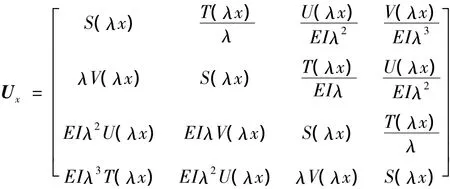
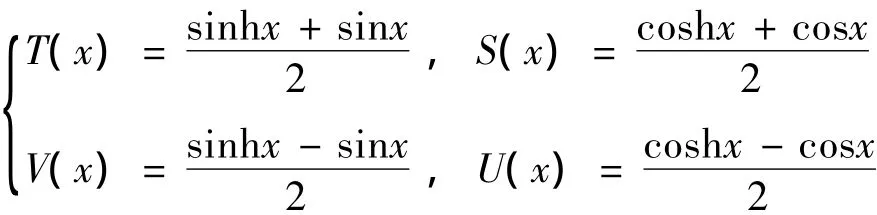
系统的总传递方程为:
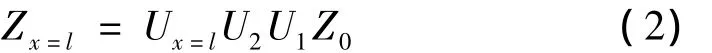
将边界条件:
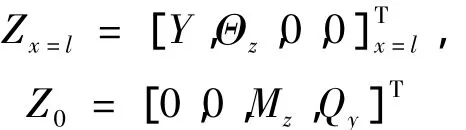
代入总传递方程,得特征方程:

数值求解上式可得系统固有频率 ωk(k=1,2,…)。对每一阶ωk,求解总传递方程可得状态矢量Z0,再由各个元件之间的传递方程可得系统任意点的状态矢量和系统振型。
建立多刚柔系统的运动微分方程:用y3(x,t)(0<x≤l)表示梁上P点的位移,y2,1(t)表示集中质量2的位移,则系统的运动微分方程为:
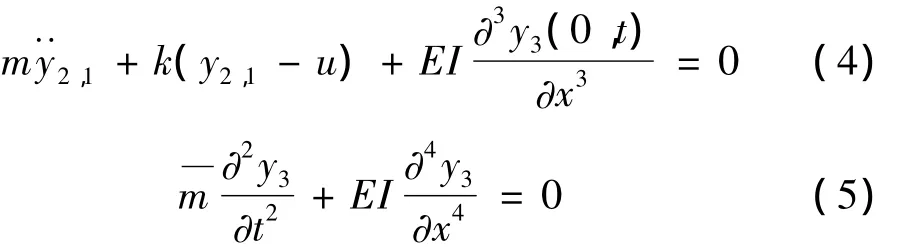
将上述方程组转化为相对基础坐标系中的方程组:
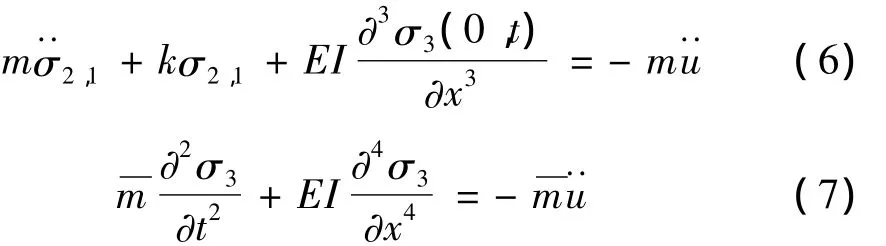
从上两式可以发现,基础加速度冲击激励已很巧妙地引入到了系统动力学方程中。
将上面动力学方程组写成体动力学方程的形式:
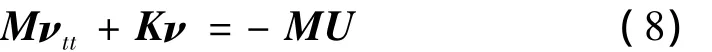
式中:
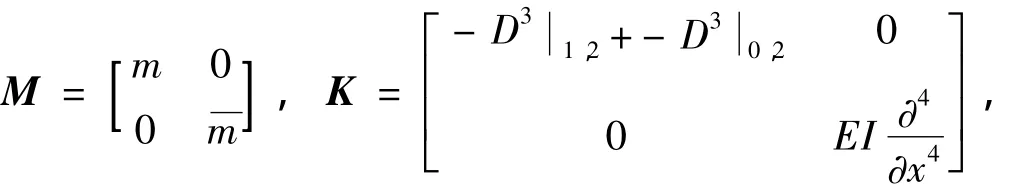
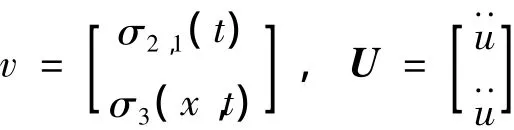
算子D3的物理意义是:当D3作用于系统中某联接点的位移时,表示体元件在该联接点处受到的除阻尼力外的所有内力,“I”表示输入端受到的内力,“O”表示输出端受到的内力。
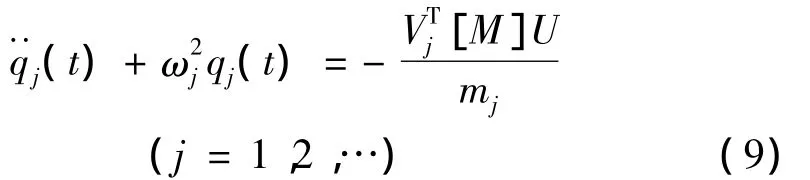
定义模态参与因子pj为:

对于零初始条件,其模态位移的解(模态系数或广义坐标)为:
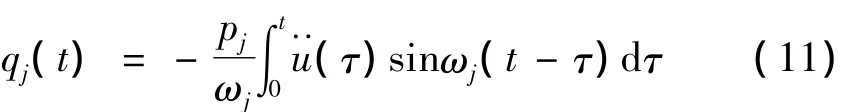
冲击速度谱由如下卷积定义[5]:
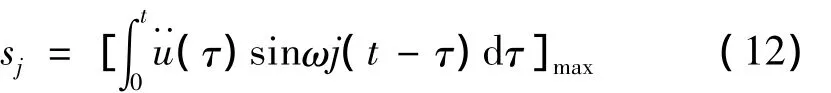
于是,最大可能的模态位移的解(模态系数或广义坐标)为:

因此,模态j的最大可能位移为:

求得冲击激励下每个振动模态最大响应后,需要对模态进行组合。在时域内,各模态贡献的代数和导致诸质量点的物理位移,可考虑相位和符号。然而,可使用各种方法来组合最大模态挠度,通常可使用下列三种方法之一:
① 绝对值求和(ABS):
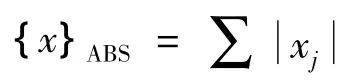
② 平方和的均方根(SRSS):
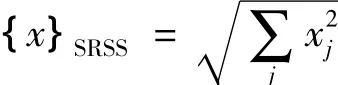
③ 美国海军研究实验室求和(NRL):
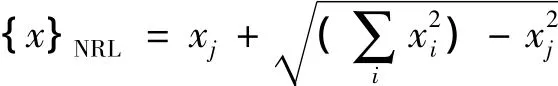
2 工程应用实例
以图1所示系统为例,取 K=615.86 N/m,m=15.6kg,l=5 m=6.24kg/m,EI=213.33 N·m2,用三种方法计算得出的固有频率如表1所示。显然,用本文中的多体系统结合传递矩阵方法得到的系统的振动特性是精确解,有限元方法的解是近似解。
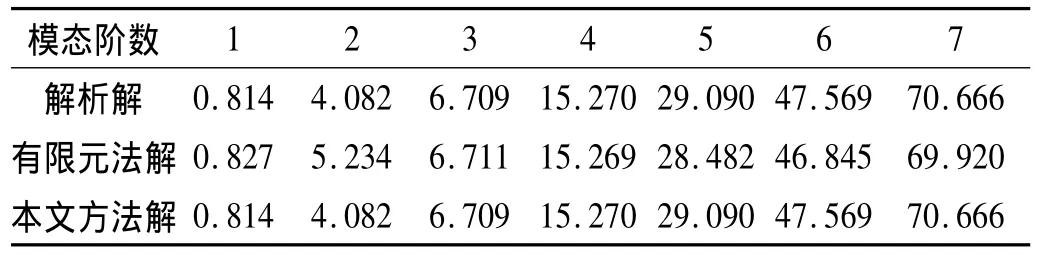
表1 固有频率计算结果/(rad·s-1)Tab.1 Natural frequencies/(rad·s-1)
系统所受冲击速度谱如图2所示,用上述参数,三种方法(解析方法、有限元法和本文方法)计算出的点4的位移响应时间历程如图3所示,取前7阶模态响应进行NRL方法合成。其他参数不变,取K=10000 N/m,计算结果如图4所示。可见,无论哪一种情况,本文方法得出的解(图3、图4中“△”表示)始终与解析解基本重合(图3、图4中粗实线),而有限元方法在第一种情况时与解析解重合较好(图3细实线),当m减小或是k增大时,有限元法的误差变大(图4细实线)。必须说明的是,这里所谓的解析解指的是按一般振动力学方法建立振动方程,然后根据响应谱分析法(模态叠加法)得到系统的响应,叠加的时候同样选用NRL合成方法。对于该工程实例来说,由于结构简单,所以可以计算得到解析解(当然,这里的“解析”也是一种近似解,因为截取的模态数有限),在计算中,我们发现,即使是如此简单的结构,解析解的表达式还是很复杂的,而本文方法只需程式化地进行元件的传递矩阵拼装,即可方便地计算出系统的固有振动特性,且固有振动特性对应于精确解析解,所以求解的动力响应精度高,这就出现了在该工程实例中解析解和本文方法计算得到的解几乎重合的情况。我们知道,对于一般的复杂系统,找到解析解是不可能的,这时候,本文方法的优越性更能得以体现。
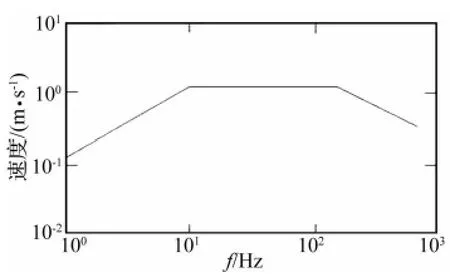
图2 冲击输入谱Fig.2 Shock input spectrum
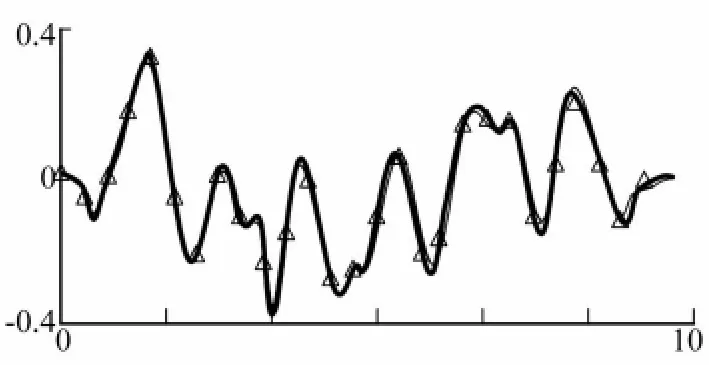
图3 梁自由端的位移时间历程Fig.3 Time-varying displacement of free end of beam
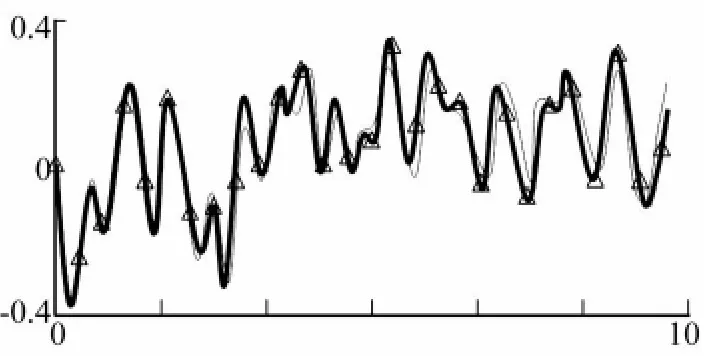
图4 k=10000 N/m时梁自由端位移时间历程Fig.4 Time-varying displacement of free end of beam when k=10000 N/m
3 结论
综合全文内容,我们可以发现,结合传递矩阵法的多体系统冲击响应谱分析法具有以下特点:
(1)涉及的矩阵阶次不取决于系统的自由度数,所以计算量比通常方法要小得多,如果对本文实例一类的链式系统,涉及的矩阵阶次仅取决于元件的矩阵阶次,这对工程计算至关重要;
(2)对于连续系统,其运动微分方程为偏微分方程,但本文方法只需求解常微分方程即可得到系统的冲击响应;
(3)本文方法可较准确地获得多体系统的真实振型和冲击响应时间历程。
[1]刘延柱,洪嘉振,杨海兴.多刚体系统动力学[M].上海:高等教育出版社,1989.
[2]Kim S J,Cho J Y,Kim W D.From the trapezoidal rule to higher-order accurate and unconditionally stable time-integration method for structural dynamics[J].Computer Methods in Applied Mechanics and Engineering,1997,149:73 -88.
[3]Fung T C.Unconditionally stable higher-order accurate collocation time-step integration algorithms for first-orderequations[J].Computer Methods in Applied Mechanics and Engineering,2000,190:1651 -1662.
[4]Lee A S,Kim B O,Kim Y C.A finite element transient response analysis method of a rotor-bearing system to base shock excitations using the state-space Newmark scheme and comparisons with experiments[J].Journal of Sound and Vibration,2006,297:595 -615.
[5]沙云东,闻邦椿,屈 伸.薄壁板在随机声载荷作用下的振动响应谱估算[J].振动与冲击,2007,26(6):63 -66.
[6]聂旭涛,熊飞峤.运用统计能量分析法预示空空导弹舱内动力学环境[J].振动与冲击,2007,26(4):140 -143.
[7]刘洪英,冯雪梅,马爱军.冲击响应谱控制系统的开发[J].振动与冲击,2006,25(6):132 -134.
[8]刘建湖.舰船非接触水下爆炸动力学的理论与应用[D].江苏无锡:中国舰船科学研究中心,2002.
[9]江国和.带限位器的舰船设备隔离系统冲击响应研究[D].上海:上海交通大学,2005.
[10]Lu Y Q,Rui X T.Eigenvalue problem,orthogonal and response of multibody system[A].Proceedings of the International Conference on Advanced Problems in Vibration Theory and Applications,Beijing:Science Press,2000:711 -714.
[11]Rui X T,Wang G P,Lu Y Q,et al.Transfer matrix method for linear multibody system dynamics[J].Multibody System Dynamics,2008,19:179 -207.
