动力模型拟静力修正方法及误差分析
2011-06-05李兆霞韩晓林
郭 力,李兆霞,韩晓林
(1.东南大学 土木工程学院,南京 210096;2.江苏省工程力学分析重点实验室(东南大学),南京 210096)
自20世纪60年代以来,国内外广大的工程师一直在追求建立精确的有限元模型来研究结构的动力响应问题。但是,由于在有限元建模过程中对结构的材料特性、构件联结形式以及外部作用进行了理想化,使得依据设计图纸而建立的有限元模型与实际结构在构件尺寸甚至结构形态上存在一定的偏差。为了提高模型的计算精度,必须对初始模型进行修正[1]。
模型修正研究工作始于1965年Guyan[2]发表的模型缩聚方面的文章,经过几十年的发展,现有的模型修正理论包括参考基准法、混合矩阵法、特征结构匹配法、特征值取逆法、误差矩阵法,贝叶斯估计等。由于修正目标的不同,各种模型修正方法间差异显著,但就具体的模型修正过程来看,模型修正方法总体上可以分为矩阵型和参数型两类。关于这些经典的模型修正方法,文献[3]中有详细的评述。
根据修正过程中依据的基本测量信息,模型修正又可分为动力模型修正和静力模型修正[4]。动力模型主要依据结构的速度、加速度、频率和振型等动态测试信息进行修正,由于这些信息能较好地反映结构的整体力学行为,因此修正大型工程结构模型时较多采用动态测量信息。但是,动态测量信息在数据采集、传输和储存过程中容易受到噪声污染,修正结果的精度需要进一步考证。静力模型修正采用的基础数据为结构在静力载荷下的位移、应力等信息。由于结构静力响应测量简单,且精度很高,因此,一般认为静力模型修正过程比动力模型修正过程精度高。
为了实现基于动态测量信息的结构模型修正,同时保持静力模型修正过程精度高的优点,本文研究如何把动力模型等效为静力模型进行修正。同时考察有限测量信息的扩展问题,分析测量误差对模型修正精度的影响程度,以建立依据动态测量信息和静力模型修正技术的拟静力模型修正方法。下面先介绍静力模型修正过程及基于复变量求导法的参数灵敏度分析方法,再研究动力模型的拟静力修正过程,进一步对修正结果的可靠性进行统计分析,最后对本文提出的方法进行数值验证,并对实际桥塔的模型进行修正。
1 静力模型修正及灵敏度分析
结构的静力响应是结构或材料参数的函数,即:

这里g为结构的静力响应,如位移、应力或应变等;x为计算模型中的参数,如材料的弹性模量、泊松比、密度和外载荷等。关于计算模型中单元间联结条件的影响,这里暂不考虑。
给定设计参数x0后,利用有限元模型由式(1)可以计算出结构的响应g0=f(x0)。另一方面,结构响应可以通过测试得到,记响应的测试值为g*。一般情况下,由于初始有限元模型存在一些待修正的误差,结构响应的计算值和测量值间有一定的偏差,记为:

依据设计图纸建立的初始有限元模型,其中的计算参数x0可以看作是结构真实参数x*的近似,由式(1)将f(x)在x0处泰勒展开,可得:
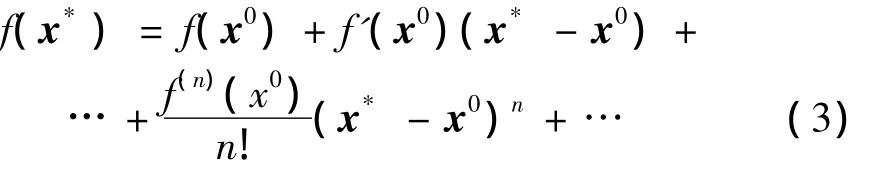
由于g*=f(x*),在上式中取一阶近似展开,则式(2)可变为:

式中 Δx=x*-x0。
令 x={x1,x2,…,xm}T,其中 xi为待修正的参数,设测量点共有n个,由式(4)可得:
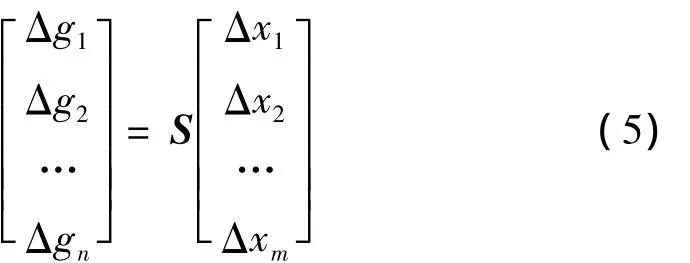
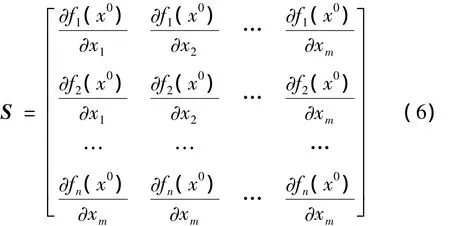
将式(5)简记为:

由于测点处的计算值和测量值已知,即Δg已知,利用式(6)求得灵敏度矩阵S后,由最小二乘法可得:
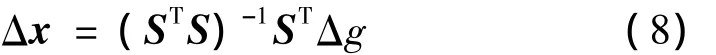
进一步可得:
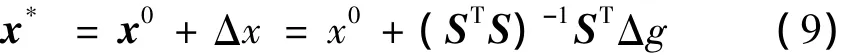
如果采用叠代求解,则相应的叠代模式为:
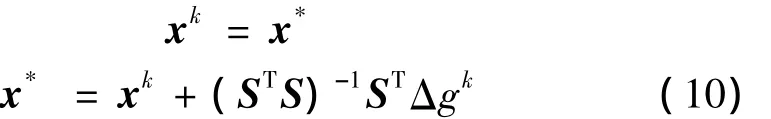
利用式(10)即可实现结构模型的参数修正。
在叠代过程中,通过残差比来判断计算过程是否收敛,残差比定义为:
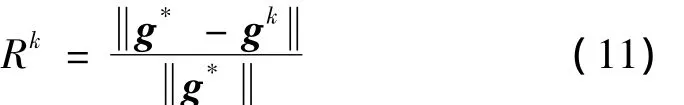
式(5)~式(11)的求解过程即为经典的基于灵敏度分析的静力模型修正过程,其中的关键是如何计算灵敏度矩阵S。由式(6)可知,灵敏度矩阵中的元素为结构响应对待修正参数的一阶偏导数。常规的基于差分法的灵敏度计算方法精度较低,且计算量较大,当结构响应对修正参数不敏感时,采用差分法将难以计算灵敏度。为了解决高精度快速计算灵敏度的问题,文献[5,6]利用复变量求导法,建立了复域灵敏度分析方法,并成功地用于结构非线性参数反演。因此,这里也采用该方法进行灵敏度分析,下面简要地给出分析过程。
对复变量函数f(x+ih),当h很小时将其泰勒展开可得[7]:
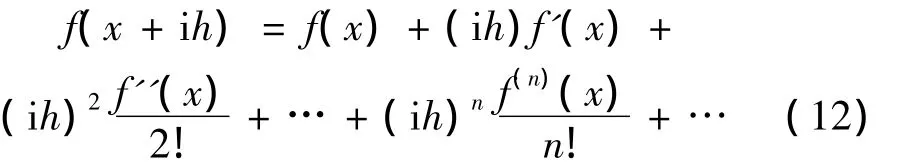
比较上式两边的虚部,可得:
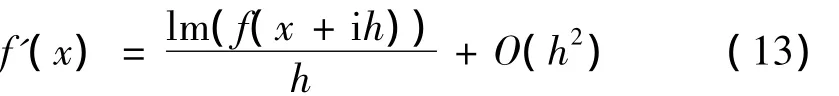
当h很小时(如10-20),由上式计算得到的函数一阶偏导数的精度为10-40,远高于计算机的机器精度,计算量是常规差分法的一半以下。
综合式(13)和式(6),可得灵敏度矩阵为:
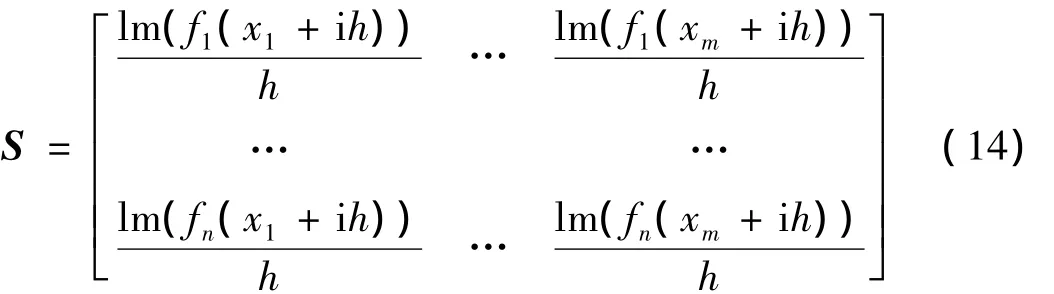
利用式(14)进行灵敏度分析时,只要把结构计算的有限元程序通过变量声明(IMPLICIT)的办法很方便地改为复变量的程序,将待计算灵敏度的参数加上很小的虚部h,提取计算的结构响应的虚部,除以h即得到结构响应对该参数的灵敏度。因此,复域灵敏度分析过程可以在结构响应计算时同时进行,对结构响应计算的程序改动量小,分析过程容易实现,在下面的模型修正过程中采用复变量求导法进行参数灵敏度分析。
2 拟静力模型修正过程
从上面的分析可以看出,静力模型修正过程简单,且精度较高。因此,如果可以得到结构的静力响应信息,尽可能采用静力模型修正方法来修正模型。但是,当结构的尺寸较大时,难以施加静载荷,且进行静力响应测量很困难,一般对大型工程结构多采用动力响应(如结构的频率和模态)测量来了解结构的力学特性。常规基于动力测量信息的模型修正过程需要构造关于结构频率或模态的目标函数,修正过程中必须计算结构的频率和模态。计算频率或模态将涉及到特征值计算问题,对大型矩阵的特征值求解过程较复杂,且存在一些固有的误差,因此,编写动力模型修正过程的程序较烦琐。如果能把测量的结构动力响应信息经过一定的转换,使得可以利用静力模型修正过程来修正模型,将显著降低模型修正过程的复杂程度,这正是本文提出拟静力模型修正方法的宗旨。下面给出转换过程。
结构自由振动时,有如下方程[8]:

其中ωi为结构的第i阶频率,K为结构整体刚度矩阵,M为结构整体质量矩阵,Φi为结构的第i阶模态。
如果在结构上施加一组载荷为:

这里Pi称为第i阶振型的特征载荷。
设Pi引起的结构位移为δi,则有:
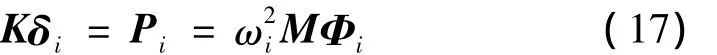
比较式(15)和式(17)可得δi=Φi,即在特征载荷作用下,结构产生的位移等于该振型的特征向量(模态)。这样,模型的特征值计算过程可以等效为在特征载荷作用下的结构静力响应计算。
在建立结构的初始有限元模型时,结构和材料参数的误差往往引起刚度矩阵K有较大的误差,对质量矩阵M的影响较小。因此,在模型修正过程中,认为系统的质量矩阵没有误差,只对刚度矩阵K进行修正。
当结构的频率和模态通过测量得到后,可以求得相应的特征载荷,即式(17)的右边已知,进一步可计算出结构的静位移δi。由于初始模型的刚度矩阵K有一定的误差,计算得到的位移一般不等于测量的模态Φi,令:

利用式(5)~式(11)的修正过程,借助上述的复域灵敏度分析过程,实现结构参数的修正。
上述模型修正的目标是实现计算模态与测试模态的高度相关,即δi=Φi。当该目标实现后,由式(17)可知,依据修正后模型计算的频率值一定高精度逼近其测量值。因此,上述修正过程最终可以实现模态和频率的双重修正目标。这样,基于动力测量信息的结构模型修正可以通过拟静力模型修正过程来实现。
采用式(16)计算特征载荷时一般需要完备的测量信息,但是,实际测量时结构的某些自由度(如转动自由度)信息很难测量。为了避免转动自由度缺失对结果的影响,在式(16)中采用集中质量矩阵进行计算。这样,在计算特征载荷时转动自由度的影响自动消除。
对于测量信息与计算信息间不匹配的问题,可以通过模态扩展的方法进行解决,文献[1]中关于此问题有详细地讨论,本文采用样条插值的办法进行模态扩展,模型修正过程中不需要进行特征值和特征向量的求解,有效降低了修正过程中的计算量。
3 误差分析
模型修正过程中依据的测量信息在测量和存储过程中往往会受到噪声污染,同时由于测量系统自身的缺陷以及外界偶然因素的影响,难免存在一定的测量误差。因此,分析测量误差对修正结果的影响是必要的。
由式(18)和式(7)可得:

假设测量中的误差是均值为0的随机误差,记为X,把式(19)两边关于X求偏导,可得:
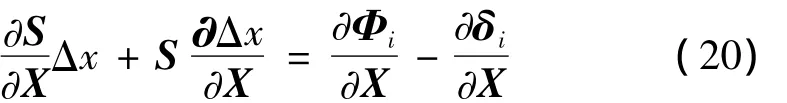
由于随机误差来源于测量过程,而δi及S由计算得到,因此有:
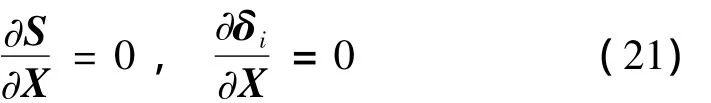
将上式代入式(20)可得:

由最小二乘法可得:
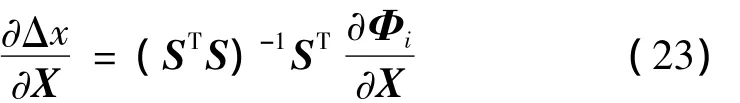
依据此式可以采用统计分析的方法来考察测量误差对修正结果的影响[9-10]。
由于这里假设测量误差的均值为0,对式(8)两边取数学期望,有:
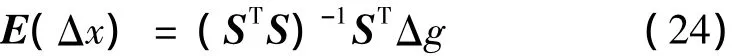
进一步可得叠代过程中修正参数的期望为:
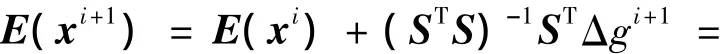
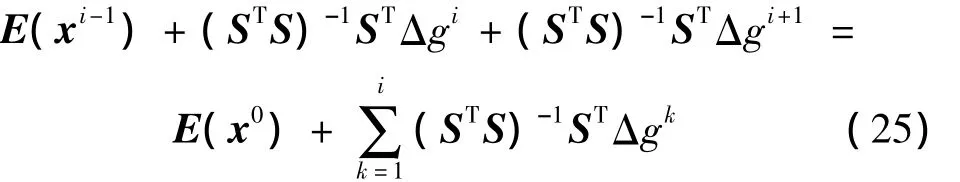
叠代过程中修正参数的方差为:
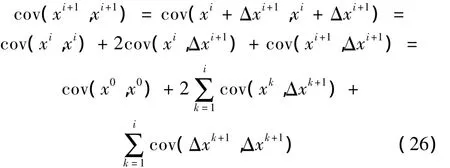
由文献[11],可知:
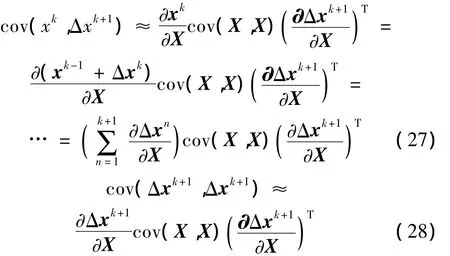
在结构测量过程中,频率的测量精度很高,这里认为频率的测量值是精确的,仅考虑模态具有测量误差的情形,因此有:
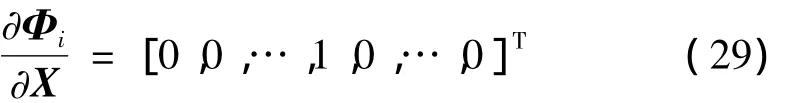
将上式结合式(23)代入式(27)和(28),进一步再代入式(26),即可求得叠代修正过程中修正参数的方差。
4 算例
为了考察上面提出的拟静力模型修正过程是否有效,考察如图1所示悬臂梁,其长度为10 m,横截面为0.1 m×0.1 m。假设梁只发生平面内弯曲,采用两节点平面梁单元进行划分,各节点的自由度为3,待修正的模型包括10个单元(图中用①,②,…,⑩表示),节点数为11个(图中用1,2,…,11表示)。悬臂粱的材料为非均匀的,其中5~7节点间材料的弹性模量为E2=180 GPa,其余部分的弹性模量为 E1=240 GPa,泊松比均为0.3,质量密度为 2.8 ×103kg/m3。
首先检验基于样条插值的模态扩展方法是否可靠。取测量自由度远低于模型的完备自由度,缺失自由度信息通过样条插值的方法产生。插值的结果如图2所示,图中的振幅为归一化振幅,将悬臂粱均匀划分为100个单元后计算的模态近似地看作真实模态(“exact curve”)。图2(a)中的测量值为一阶振型中4、7、11三个节点处的横向振动信息,图2(b)中的测量值为二阶振型中3、6、9、11四个节点处的横向振动信息。可以看出,插值得到的模态与真实模态吻合很好,因此可以认为基于样条插值的模态扩展方法是可行的。

图1 悬臂梁及其有限元模型Fig.1 Cantilever and its FE model
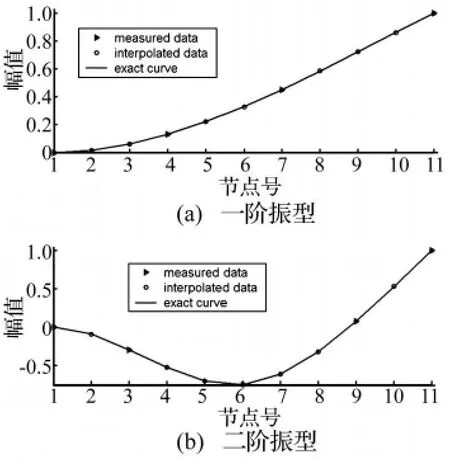
图2 样条插值模态与测量模态Fig.2 Spline interpolated modals and measured ones
利用样条插值扩展得到模态后,可进一步利用式(16)计算特征载荷。但是,这里的模态为归一化模态,必须转化为正则化模态后才可用于特征载荷计算。转化过程中质量矩阵取为有限元模型的集中质量阵,由于过程简单,这里不再具体列出。
初始有限元模型中,取E1=E2=200 GPa,其余参数取为真实值,利用上述的拟静力模型修正过程对该模型进行修正,修正时仅依据一阶模态中测点处的信息进行修正,修正过程中弹性模量的变化情况如图3中“E1”和“E2”所示,可以看出,相应参数均收敛于真实值。
为了考察测量噪声对修正结果的影响,把测量信息中加入强度为2%的白噪声,相应的弹性模量的修正结果如图3所示,其中的“ER1”和“ER2”即为包含测量噪声的弹性模量E1和E2修正值。由于测量噪声的影响,弹性模量无法精确修正到真实值,但总体来说,修正结果仍然很好地逼近真实值。E1和E2修正后与真实值的相对误差分别为0.37%和3.8%,其中E2的相对误差相对高一些的原因是模型中仅有两个单元的弹性模量为E2,结构响应对参数E2的变化不敏感,因此测量噪声对E2修正结果的影响更大些。
修正过程中参数E1和E2的方差由式(26)计算可得,其变化情况如图4所示,其中“cov1”和“cov2”分别代表弹性模量E1和E2的方差,可以看出它们的方差均很低,因此,可以认为修正结果的可靠度很高。
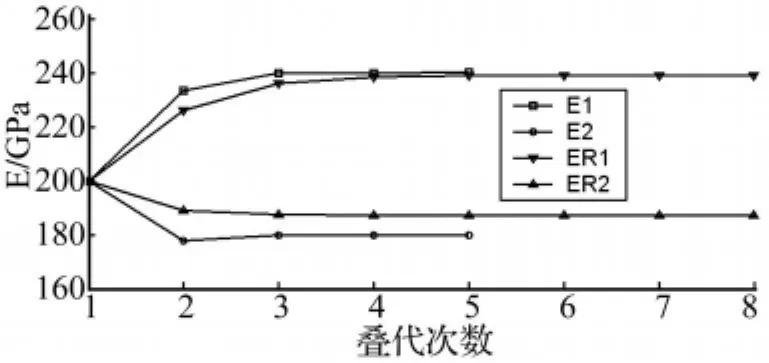
图3 修正过程中参数变化情况Fig.3 Model parameters history in updating process
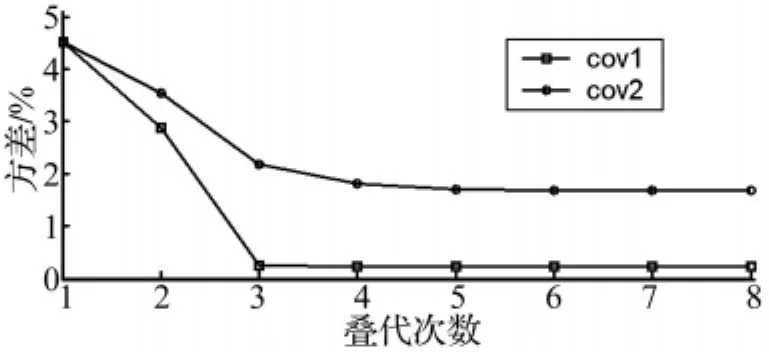
图4 修正过程中参数方差Fig.4 Parameters variance in updating process
从上面的算例可以看出,提出的拟静力模型修正方法能有效地实现基于动力测量数据的结构模型参数修正。用该方法来修正润扬长江大桥北汊斜拉桥的桥塔有限元模型。润扬大桥斜拉桥桥塔净高143 m[图5(a)],对于高耸的大型结构无法用常规的人工激励振动的方法进行测试,而采用环境激励振动测试的方法。测试系统选用13只941B型伺服式超低频加速度传感器,其中一只传感器作为参考点,其余12只传感器按图5b所示方式布置,测量方向为水平方向,测试过程按测量方向分为顺桥向和横桥向两个部分进行。信号采集与分析采用AZ-Cras振动与动态信号采集系统,采用环境激励下的模态识别方法进行参数识别。
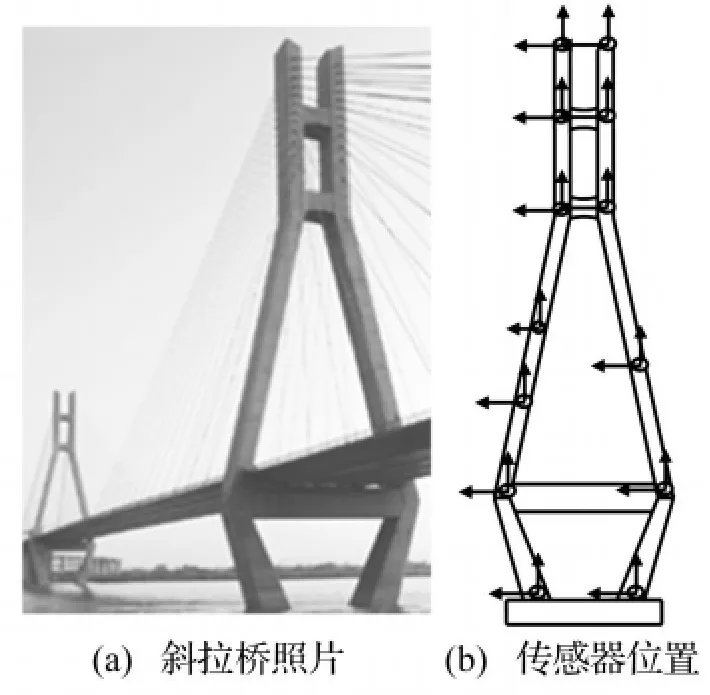
图5 润扬大桥斜拉桥及桥塔传感器位置Fig.5 Runyang cable-stayed bridge tower and its sensors location
在各测点信号与参考点信号之间互谱分析的基础上识别桥塔结构的固有频率和振型,模态振型(前4阶)如图6所示。
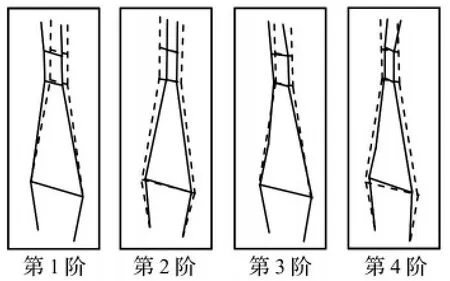
图6 识别的桥塔振动模态Fig.6 Identified modals of bridge tower
在建立润扬斜拉桥桥塔有限元模型时,考虑到桥塔属于高耸结构,截面尺寸相对于自身纵、横向尺寸较小,因此采用了空间二节点等参梁单元,共86个单元。
由于桥塔是钢筋混凝土结构,各部位的钢筋配比率以及施工过程中的养护条件有所差异,因此各部位相应的材料参数可能差别较大。在建立有限元模型时,对上、中、下塔柱以及三个横梁采用不同的材料参数,因此待修正的参数共有6组。由于施工过程中钢筋的配比量及混凝土的标号已知,相应区段的平均质量密度可以较准确地确定,这样,在建模过程中各区段的材料密度按计算的平均密度给定,模型修正过程中不考虑密度参数的误差,仅修正各区段的抗弯刚度,共12个参数。
在样条插值扩展模态时,为了降低插值运算量,对塔柱的上、中、下三段分别进行插值,这样,由于插值点与测量点在一条直线上,插值计算量得以降低。横梁上的点插值时,由于各个横梁的两个端点均为测点,容易进行插值。
由于桥墩墩台处的测量信号较弱,修正时没有采用墩台上2个测点处的信息,其余11个测点处的信息均作为响应的测量值来修正模型。由于待修正的参数共12个,任一阶模态的11个测点共有22个测量值,完全可以满足参数的修正需要。为提高修正模型的精度,这里采用了前两阶的模态测量值进行修正,修正后各区段的参数如表1所示。表中的“EI11”和“EI22”分别为构件横截面绕形心主惯性轴的抗弯刚度。
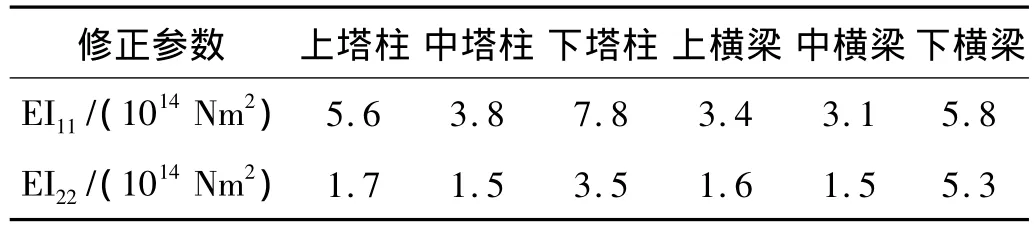
表1 模型参数的修正结果Tab.1 Results of updated model parameters
为了检验修正结果的精度,根据修正得到的模型参数,利用ABAQUS软件选取工程粱单元建立了桥塔结构的有限元模型,网格划分与修正模型的一致,计算的频率值及模态如表2所示,表中“MAC”表示计算模态与测量模态的相关程度[4],可以看出修正后模型的计算值与测试值吻合良好,其中第1、2阶模态的计算值和测试值相关性很高,这主要是因为修正过程中直接采用了该两阶模态的测量值进行修正。虽然第3、4阶模态的测量值在模型修正过程中没有直接采用,但可以看出计算值与测量值仍然很接近,这从另一方面也证明了修正结果的正确性。
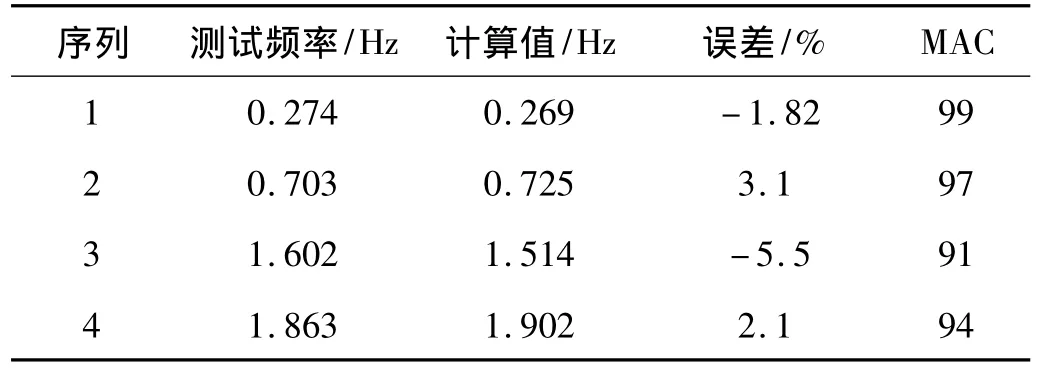
表2 修正模型的计算结果和测量值Tab.2 Computed results with updated model and the measured ones
对于修正结果的统计分析,由于测量过程中的误差信息无法得到,这里假设测量过程中有方差强度为2%均值为0的白噪声。利用式(26)计算参数修正过程中的方差情况,方差较大的为下塔柱的抗弯刚度EI11,叠代修正结束时其方差为5.7%,表明在修正后的下塔柱参数中尚有部分未确定因素没有消除。下塔柱实际上是变截面构件,而有限元模型中近似处理为等截面构件,这一近似过程使得修正结果具有一定的未确定性。要进一步降低相关的未确定因素,可以把下塔柱细分为结构参数不同的几段,通过进一步地修正来降低其未确定性,这样处理会增加待修正参数的数目,造成修正过程的计算量较大,在工程精度允许的前提下,可以适当损失一定的精度而采用简单模型。关于参数细分问题的研究这里不做进一步展开。
5 结论
本文提出了拟静力模型修正方法,借助特征载荷概念,将基于动力特性测量信息的较为复杂的动力模型修正转化为静力模型修正,避免了模型修正过程中特征值和特征向量的计算问题,降低了修正过程的复杂程度。对修正过程中测量信息和计算信息间的匹配问题,通过样条插值的办法加以实现。采用复域灵敏度分析法,解决了修正过程中参数灵敏度高效计算问题。对参数修正过程中的误差进行了统计分析,为评估修正结果的可靠性提供了基础。数值算例表明,拟静力模型修正方法进行参数修正时需要的测量信息有限,利于实际工程结构模型的修正。对润扬大桥北汊斜拉桥桥塔模型进行了修正,与测量值对比表明修正结果较为精确可靠。
[1]Mottershead J E,Friswell M I.Model updating in structural dynamics:a survey[J].Journal of Sound and Vibration,1993,167(2):347-375.
[2]Guyan R J.Reduction of stiffness and mass matrices[J].American Institute of Aeronautics and Astronautics Journal,1965,3(2):380.
[3]朱安文,曲广吉,高耀南,等.结构动力模型修正技术的发展[J].力学进展,2002,32(3):337-348.
[4]郭 力,李兆霞,陈鸿天.基于子结构分析的多重子步模型修正方法[J].中国工程科学,2006,8(9):42-48.
[5]Gao X W,Liu D D,Chen P C.Internal stresses in inelastic BEM using complex-variable differentiation [J].Computational Mechanics,2002,28(1):40 -46.
[6]郭 力,高效伟.复变量求导法灵敏度分析及弹塑性参数反演[J].东南大学学报,2008,38(1):141-145.
[7]Lyness J N,Moler C B.Numerical differentiation of analytic functions[J].SIAM Journal of Numerical Analysis,1967,4(2):202-210.
[8]朱伯芳.有限单元法原理与应用,第二版[M].北京:中国水利水电出版社,1998.
[9]Li X Y,Law S S.Damage identification of structures including system uncertainties and measurement noise[J].AIAA Journal,2008,46(1):263 -276.
[10]Law S S,Li X Y,Lu Z R.Structural damage detection from wavelet coefficient sensitivity with model errors[J].Journal of Engineering Mechanics,2006,132(10):1077-1087.
[11]Papadopoulas L,Garcia E.Structural damage identification:a probabilistic approach[J].AIAA Journal,1998,36(11):2137-2145.
