硅片传输机器人的分析设计

马喜宝

(上海微高精密机械工程有限公司，上海 201203)

随着科学技术的发展和社会的进步，机器人的应用越来越普及，它不仅广泛应用于工业生产、航天、海洋探测、危险或条件恶劣的特殊环境中，且已逐渐渗透到日常生活及教育娱乐等各个领域，特别是近十几年随着IT产业的飞速发展，高速度、高定位精度、高可靠性和高洁净度的机器人广泛应用于光刻、清洗、划片、测试等电子专用设备上，进行硅片、基板、掩模版等物料的传输。本文重点介绍型硅片传输机器人的结构设计，并对其进行运动学和动力学的分析。

1 硅片传输机器人机械结构分析与设计

R-θ型硅片传输机器人具有二自由度运动功能：R向径向运动；θ向旋转运动。其中，最主要的是R向径向运动，是由电机通过带传动驱动前、后臂的关节同时回转，实现末端沿径向做直线运动；而θ向旋转运动是由电机通过带传动进行旋转运动。下面利用机器人学的基本理论重点对径向直线运动进行分析，并根据分析结果进行相应的结构设计。

1.1 机器人操作臂的运动学与动力学分析

要实现硅片传输机器人末端执行器径向直线伸缩运动的高精度和高可靠性，就必须对操作臂进行相关的动力学分析，以确定前后操作臂的长度和旋转角度的大小和方向。首先建立串联三连杆机构的数学模型，如图1所示。

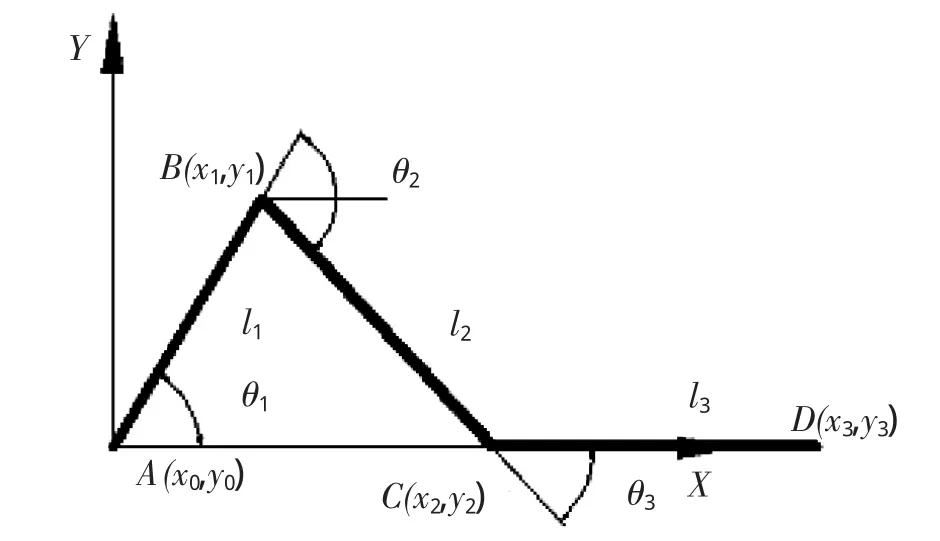
图1 串联三连杆机构数学模型

根据图1中对三连杆机构的简化模型（角度为矢量角），C(x2，y2)、D(x3，y3)两点的坐标可以表示成：

已知末端操作手即杆作往复直线运动，故可知：y2=y3。于是有：sin(θ1+θ2+θ3)=0，

即：

又因为点A、C、D共线可得：

将方程组(1)代入式(4)展开化简得：

至此式(2)及(5)是末段杆CD沿图1坐标系X轴做往复直线运动的约束关系式。

不妨令 θ2=aθ1,θ3=bθ1，代入式(5)有：

其中l1，l2均为杆长，是常数。

为确定以上比例式中的a，b的值，不妨令前后臂长相等l1=l2，于是得到a=-2b。

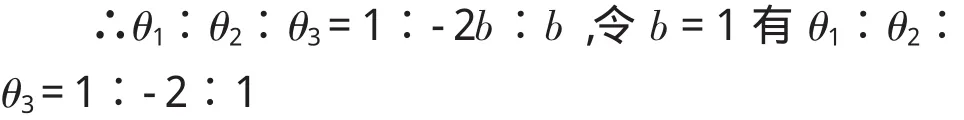
最后推倒出完成径向运动的三连杆机构末段杆做往复直线运动的必要条件：

从式(6)可以看出，要想实现径向直线往复运动，前臂和后臂的臂长应相等；三个转角之间的比值为1∶-2∶1。也就是说从运动输入后臂至末端执行器输出，两套带传动的传动比依次为1∶2及2∶1，其中负号所代表的是前臂l1与后臂l2转动方向相反，与末端执行器l3转向一致。

1.2 硅片传输机器人径向机构的运动学分析

综合前面的分析，使用三连杆和两套同步齿型带传动方可实现该径向直线运动，如图2所示。其中，带轮5和7设置在后臂杆4上，带轮5固定不动，带轮7除绕其转轴自转外，还随后臂的转动作为行星轮转动；带轮9和带轮11设置在前臂杆8上，带轮9的转轴和后臂4通过轴承连接，同时和前臂8固连，带轮9、转轴和前臂8可一起绕转轴中心转动。带轮11和其转轴以及末端执行器12固连。根据前面的推导，设置带轮5与7间的传动比为1∶2，带轮9与11间的传动比为2∶1，两套同步带传动的传动中心距l1=l2=L。

下面利用微分几何理论中关于坐标变换的基本方法来分析末端执行器12的运动学特性，如图2所示，静止的参考坐标系(X,O,Y)固定在带轮5上；动系(X1,O1,Y1)固定在后臂4上，由于后臂4是原动件，设其绕O点转速为ω，方向逆时针，即动系(X1,O1,Y1)相对参考坐标系(X,O,Y)以角速度ω转动，转角 θ1=ωt，得到动系(X1,O1,Y1)相对参考坐标系(X,O,Y)的坐标转换矩阵：

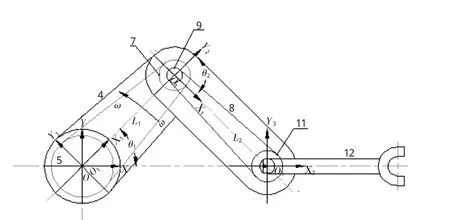
图2 硅片传输机器人径向直线运动机构图

动系(X2,O2,Y2)固定在带轮9（前臂8）上，因此动系(X2,O2,Y2)相对于动系(X1,O1,Y1)只有绕点O2的转动，带轮5与7间的传动比为1∶2，显然带轮7自传转速为2ω，方向顺时针，转角θ2=2ωt，得到动系(X2,O2,Y2)相对动系(X1,O1,Y1)的坐标转换矩阵：

动系(X3,O3,Y3)固定在带轮11（末端执行器12）上，因此动系(X3,O3,Y3)相对于动系(X2,O2,Y2)只有绕点O3的转动，带轮9与11间的传动比为2∶1，显然带轮7(带轮9)自传转速为ω，方向逆时针，转角 θ3=ωt，得到动系(X3,O3,Y3)相对动系(X2,O2,Y2)的坐标转换矩阵：

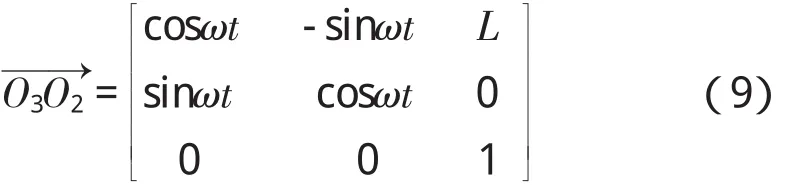
通过上面推导的三组坐标转换矩阵(7)(8)(9)，可以得到动系(X3,O3,Y3)相对于参考坐标系(X,O,Y)的坐标转换矩阵：

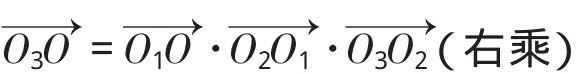
从与末端执行器12固连的动系(X3,O3,Y3)相对于参考坐标系(X,O,Y)的坐标转换距阵(10)可以看出，姿态阵是一个单位阵，说明末端执行器12相对静止参考坐标系没有转动，并且位置阵[2Lcosωt,0,1]T反映出，末端执行器12只有沿X轴的位移，沿Y轴没有位移，这充分证明了机构的设计方式完全实现了末端执行器沿径向（X轴）作直线传输运动。并且位移S=2Lcosωt，求导得到速度表达式：

由上述运动学分析，要实现径向直线伸缩运动，结构设计中必须满足式(6)的条件：

（1）l1=l2=L，需保证前后臂体转轴孔距相等。

（2）θ1∶θ2∶θ3=1∶-2∶1，需使用同步带传动。

1.3 硅片传输机器人径向机构的动力学分析

首先建立硅片传输机器人手臂的动力学模型，如图3所示。图中m4为后臂4质量；m8为前臂8的质量；m12为末端执行器12的质量；l4为后臂4长度；l8为前臂8长度；l12为末端执行器12的长度；θ1为后臂4角位移；θ2为前臂 8的角位移；θ3为末端执行器12的角位移。

坐标系X0OY0为机器坐标系，与机械手基座固连，此时作为静止坐标系，坐标系XOY为手臂坐标系，其X轴始终指向机器人的手臂径向运动方位。在图示的运动瞬间，设机械手θ向角位移为a，R向角位移θ1。因此，坐标系XOY相对坐标系X0OY0应该有转角a，但θ向转动并不影响机θ1器人的R向运动，即手臂的动力学分析可以在假设坐标系XOY静止的情况下进行。

由于机器人的操作手臂将采用铝合金制作，质量较轻而且分布均匀。所以在动力学分析中，为了简化动力学分析的复杂程度，将前臂、后臂以及末端执行器都简化成形状简单、质心位于几何中心的直线杆件，如图3。

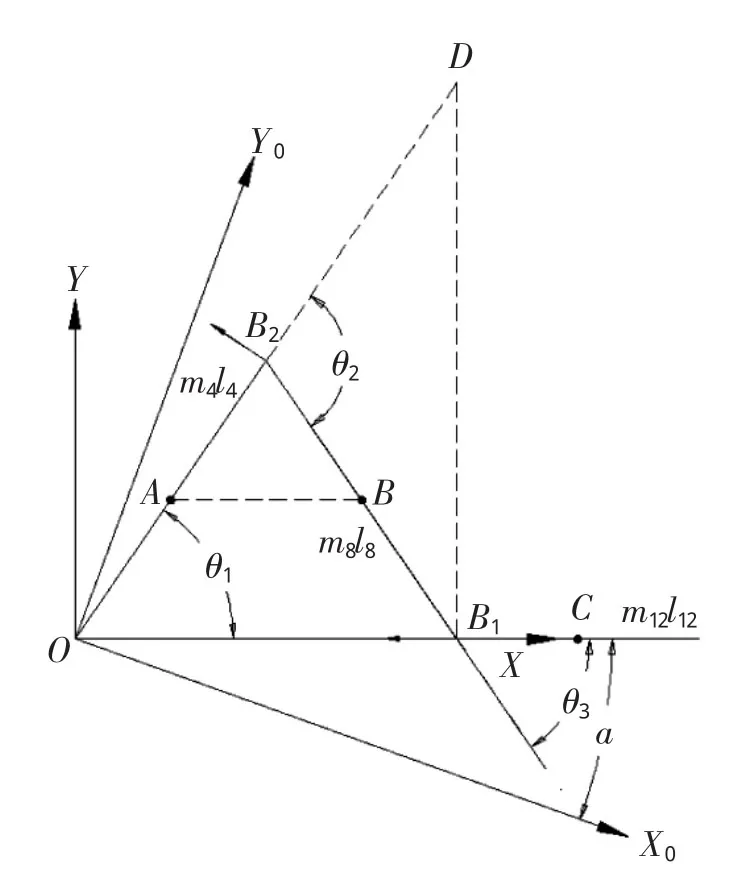
图3 机器人手臂动力学模型

为确定驱动机器人R向运动所需的电机力矩和控制系统设计的需要，下面采用分析动力学中的拉格朗日方程来推导手臂的动力学方程，从而建立机器人动力学模型。拉格朗日方程采用动能和广义力来表示，应用它可以方便的得到与系统自由度相同，相互独立的运动微分方程。

式中：T为刚体系统的总动能，qj为系统中的广义坐标，Qj为广义力。

（1）判断系统的自由度并选取广义坐标。从图3可以看到，在手臂的运动中，变化的是三杆及坐标轴X间的3个夹角，但是由于要满足径向直线运动的必要条件，3个夹角间有比例约束关系θ1∶θ2∶θ3=1∶-2∶1。把手臂看成是单自由度刚体系统，选取θ1作为广义坐标。

（2）系统的动能方程。后臂4绕O点定轴转动，其动能为：

计算前臂8的动能，由于前臂8运动复杂，取其几何中心B为质心，因此前臂8的动能可以看成是刚体绕质心B旋转的动能与质心B平移动能之和。从图1～3中可知，D点是前臂8两端点B1和B2速度方向垂线的交点，因此D是前臂8的瞬心，不难证明DB2=B2B1=L，可以得到前臂8绕速度瞬心D的转动角速度就是ω=θ'1。对刚体平面运动而言，可以把转动基点设在质心B处，则前臂8绕质心B的转速也为ω=θ'1。

前臂8绕质心B的旋转动能记为：

如图3由于质心B位于等腰三角形OB2B1的中位线上，通过几何关系容易列出B点的位置方程为：

求导得B点速度，

杆8质心B的平移动能记为：

计算末端执行器即杆12的动能，显然杆12沿X轴平动。由于在前面运动学分析中已经知道杆8作径向直线运动，速度表达式：

V=2ωLsinωt，由于 ω=θ'1

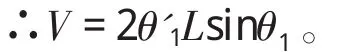
动能记为：

操作臂的总动能记为：

杆8的总动能记为：

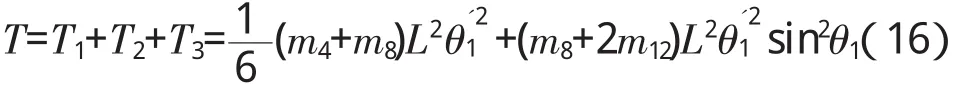
（3）带入拉格朗日方程：

在拉格朗日方程中，由于机器人手臂是单自由度刚体系统，根据虚功原理可以知道广义力Q1=N1，其中的N1就是径向直线运动需要的扭矩，即：

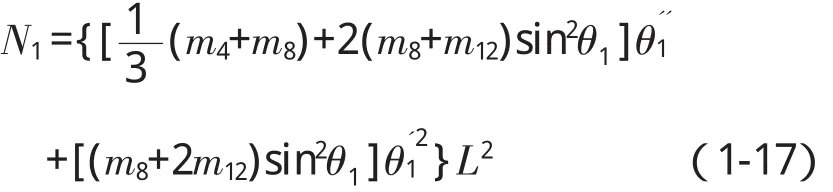
从上式中可以看出，只要知道后臂的角加速度和角速度，就可以得到硅片传输机器人径向直线运动部件运动所需要的扭矩。该动力学方程可以用来估计以一定角速度和角加速度驱动机器人手臂各个关节所需要的扭矩，对硅片传输机器人R向部件驱动器和电机选择具有指导作用。尤其对于控制和保证机器人优良的动态特性和静态特性，以及机器人的工作精度、稳定性具有重要的意义。

2 硅片传输机器人机械结构设计

2.1 机械结构设计的基本原则

硅片传输机器人的主要应用在超大规模集成电路生产线上，必需具备高精度、高速度、高效率、高洁净度和质量轻的特点，因此在结构设计方面必须考虑以下因素：

选用精密的驱动和传动元件、灵敏的检测传感器以提高其精度；合理设定机器人主要结构的固有频率，保证传输过程的平稳，提高机器人的运行速度；合理设计控制系统，进行最优路径规划，提高传输效率；选用阳极氧化的硬铝和不锈刚等对洁净室无污染的材料，整体采用包覆式机壳，防止摩擦产生的尘粒外泄，减少振动造成的尘粒对环境的影响，提高机器人的洁净度；在满足机器人运动功能的前提下，以重量最轻为原则对机械部分包括运动部件、传动部件和驱动元件等进行结构的优化设计。

2.2 R-θ机械人基本结构

R-θ机器人既可以沿旋转半径R方向进行直线运动，也可以绕轴线进行旋转运动，且互不干扰，使末端执行器能到达XY平面内的任意一点，其结构如图4所示，主要由R向电机、θ向电机、θ向带轮 1、齿型带 2、θ向带轮 3、后臂 4、带轮 5、齿型带6、带轮 7、前臂 8、带轮 9、齿型带 10、带轮 11、末端执行器12、转轴13、转轴14、顶部安装法兰15、转轴16、中心轴17、电机座18、保护罩19组成。

2.3 R-θ机器人运动原理

θ向电机的运动通过向带轮1、齿型带2和θ向带轮 3，传递到转轴 16，后臂 4、带轮 5、转轴16、中心轴17、电机座 18、R向电机等和转轴 16固定在一起，随θ向电机的转动，机器人机械臂和末端执行器12完成θ向的转动。

R向电机的运动通过中心轴17，驱动后臂4绕中心带轮5转动，此时带轮5相当于恒星带轮，和带轮7通过齿型带6连接在一起，带轮7和转轴14通过轴承和后臂4连接。后臂4的转动就形成带轮7和转轴14绕带轮5作行星转动，同时也绕转轴14作自传运动，转向和后臂4方向相反，转角是后臂4转角的二倍；前臂8和带轮9同转轴14固定在一起，形成一个整体。带轮11、末端执行器12和转轴13固定在一起，形成一个整体。这两个整体结构通过齿型带10连接。前臂8的转动就形成带轮11、转轴13和末端执行器12绕带轮9作行星转动，同时也绕转轴13作自传运动，转向和前臂8方向相反，转角是前臂8转角的二分子一倍。随R向电机的转动，机器人机械臂和末端执行器12完成R向的直线运动。

R和θ的所有运动部件固定在顶部安装法兰15上，安装法兰15设计有螺钉安装过孔，可用于机器人整体结构的安装固定；保护罩19将R向电机和θ向电机等其它零部件和电器接插件密封在一个整体腔体内；后臂4和前臂8上分别固定有盖板，将带轮、轴承和转轴进行密封，有利于机器人安全运行和防止颗粒、粉尘等污染物的产生。

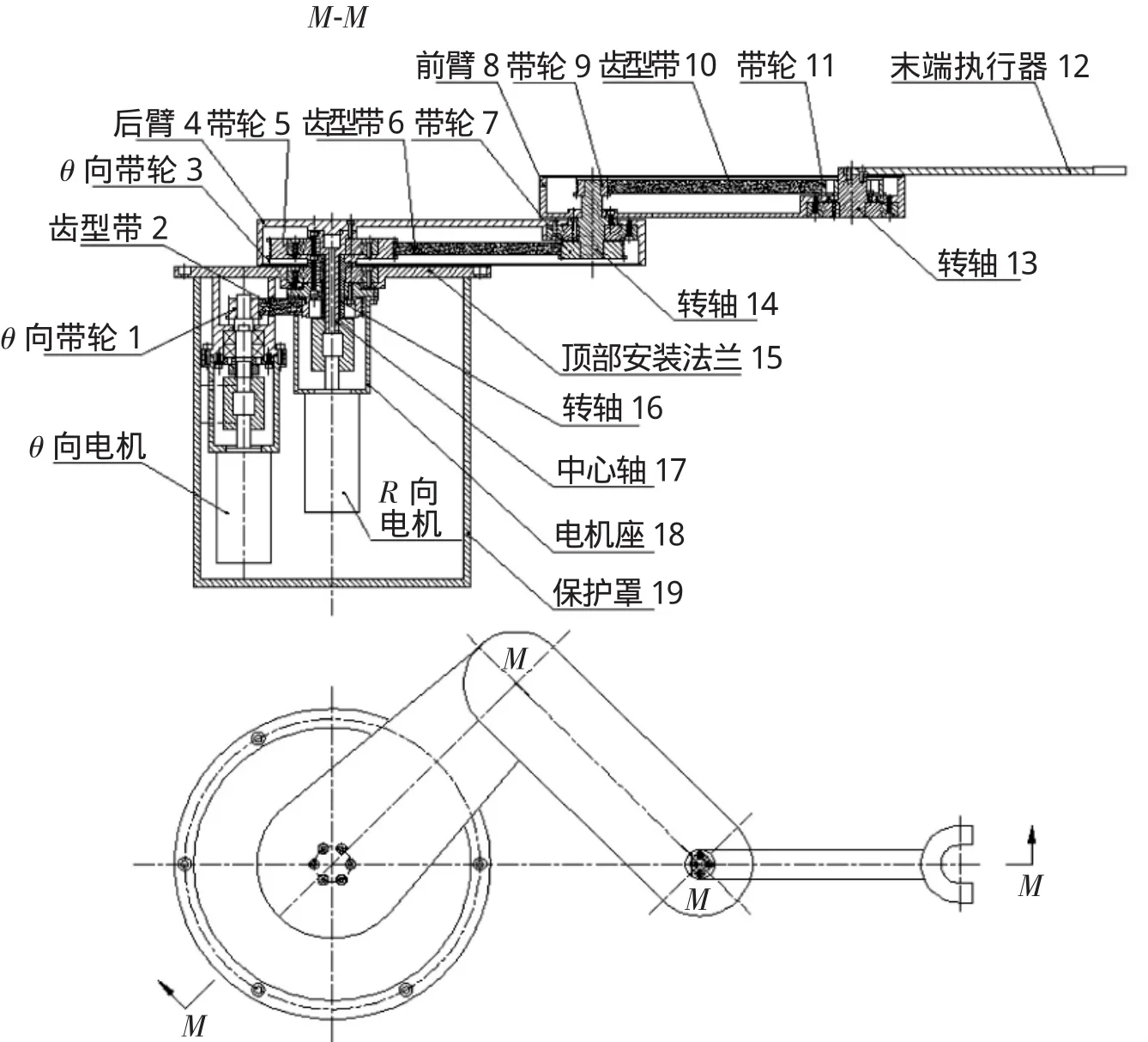
图4 机器人基本结构

3 结束语

本文主要针对硅片传输单臂二自由度机器人在XY平面内运动时的结构状况，在大多数情况下，硅片传输机器人还需具有三自由度的运动轨迹，即在垂直XY平面的Z向进行运动，以适应不同高度工位之间的硅片传输。为提高传输效率，还可以再增加传输臂，做成双臂机器人；为了增加工位减小运动所需空间，在单臂机器人的末端执行器上再增加驱动电机，就可以形成四个自由度的机器人。这些工位的增加都是在二自由度机器人结构的基础上进行，都必须满足二自由度机器人的运动学和动力学特性，总之，硅片传输单臂二自由度机器人是多自由度机器人的基础，对其进行结构设计和运动分析，为以后更深入的探索和研究多自由度的机器人，提供一些参考。