光刻设备中硅片预对准的算法模型分析

张鹏远，杨 林

(上海微高精密机械工程有限公司，上海 201203)

预对准为硅片传输分系统重要部件之一，负责完成硅片预对准功能，以确保传送到工件台的硅片偏心和偏向在预定的精度范围内。其主要功能包括硅片交接、预对准功能。本文详细描述了通过采集硅片边缘和缺口的形貌数据，计算硅片形心、缺口位置，进而修正硅片的偏心及偏向的算法。本方法预对准时间短、精度高。并在实际工程中已验证可行性。

1 预对准基本原理

通过采集硅片边缘和缺口的形貌数据，计算硅片形心、缺口位置，进而修正硅片的偏心及偏向。预对准算法示图如图表1所示。

图1 预对准算法示意图

流程如下：

（1）转台通过真空吸附硅片，并带着硅片旋转1周（转台角度θ从0到2π），装在硅片边缘附近的线阵CCD同步采集硅片边缘形貌数据，各采样点离转台中心距离为 Ri，(i=0~n，n=2000)，对应的转台角度θi。这n个数据绘制出的图形通常如图1右侧的边缘数据的黑色部分。白色缝隙对应硅片缺口；

（2）在硅片边缘形貌数据中进行图像匹配，找到缺口所在位置；

（3）将缺口数据用相邻形貌数据补偿后，计算硅片形心；

（4）将硅片形心转到定心台运动方向与转台中心的连线上；

（5）将硅片交接到定心台；

（6）通过定心台的运动补偿偏心；

（7）将硅片交接到旋转台；

（8）将硅片缺口转到CCD附近，采集硅片缺口数据；

（9）采集硅片缺口数据（类似步骤1，转角略比缺口大），计算缺口质心位置；

（10）将缺口质心转到最终位置（需考虑预对准坐标系、工件台坐标系的关系以及用户指定的附加角度）。

2 缺口检测

首先要确认硅片缺口的形状。通过对等腰三角形、圆弧形和抛物线形三种情况进行仿真分析。三种情况仿真结果略有差别，且抛物线形与实际情况最为接近，固以下仿真采用抛物线形，数据如图2所示，其他形状缺口仿真结果不再详述。

差分发：因为采集到的点是均匀分布的，相临两点到原点的距离相差不大，而缺口边缘的点与相邻点到原点的距离相差较大。所以设定合适的阈值就可以判定出缺口两端点，从而确定哪些是缺口中的点。

设 R（n）为采样点的半径值数组，D（n）为一阶差分数组，threshold为阈值。对采样点做一阶循环差分：

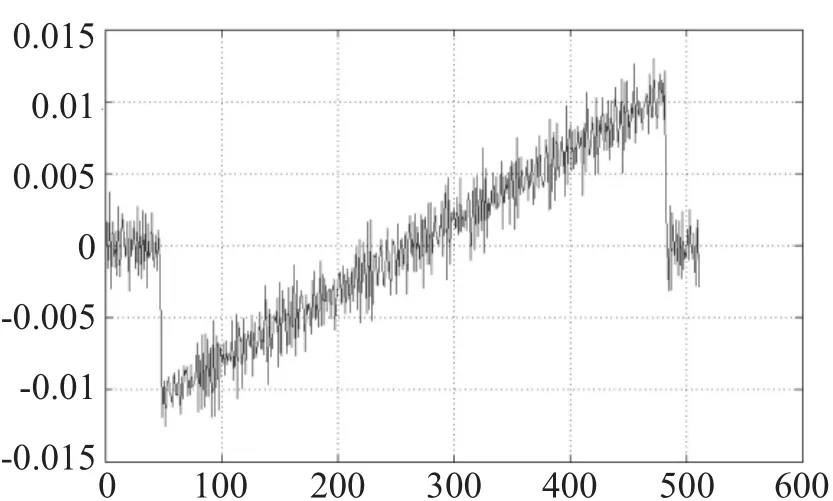
图2 差分法采集数据分析

边缘变化率法：因为采集到的点是均匀分步的，所以任意3点之间的夹角趋于一致，而缺口上点的夹角有较大变化。所以通过设定合适的阈值可判断出哪些是缺口上的点。边缘变化率最大的点即为缺口中心的初始估计值。

设 3 点分别为 A(x1，y2)，B(x2，y3)，C(x3，y3)。

则BA和BC之间的夹角为：

数据分析如图3所示。

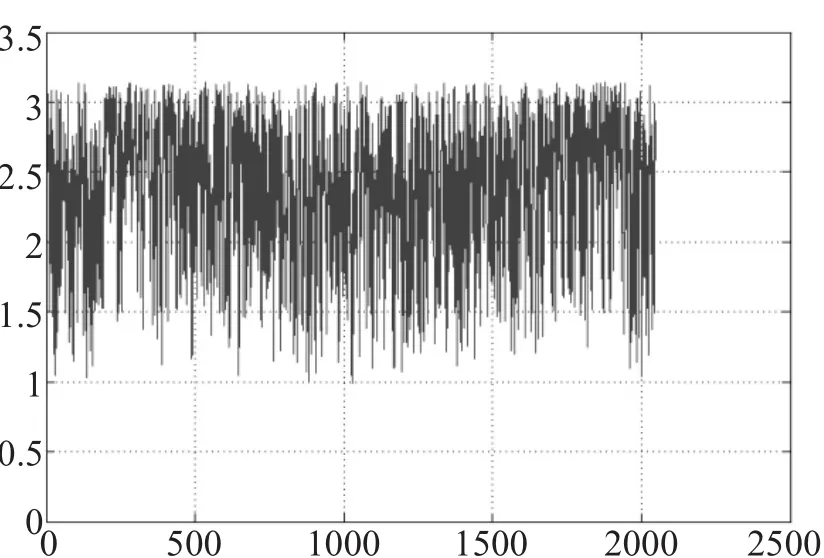
图3 边缘变化率法数据分析

从图中可已看出，很难找到端点位置，并且有时计算数据会得到复数。

3 硅片形心计算

硅片形心计算采用最小二乘法，算法如下：设x，y为采样点的坐标值，n为采样点数，则有：

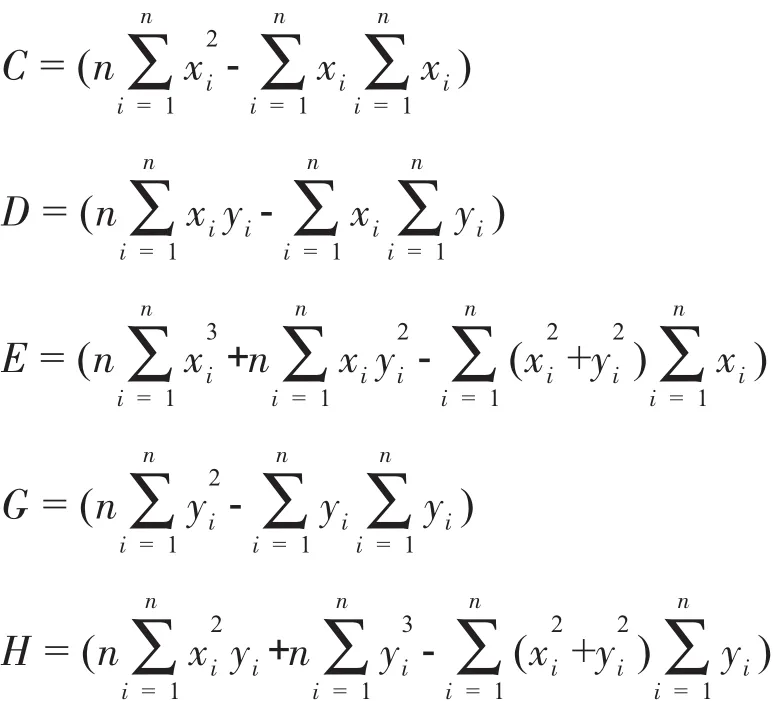
求解可得：

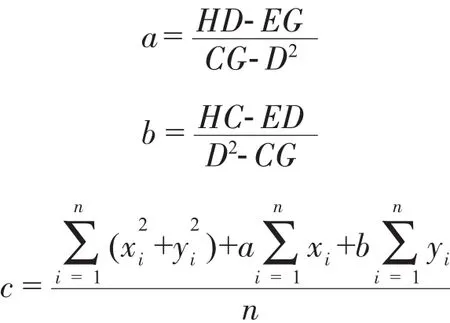
所以求得：

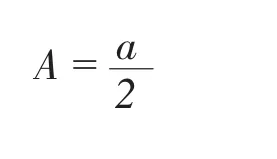
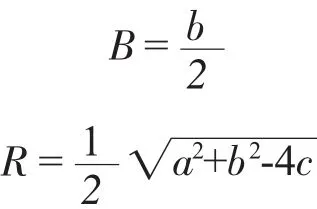
则圆心直角坐标(A，B)及圆心半径R既可求得。仿真1000次，偏心距数据如图4所示。

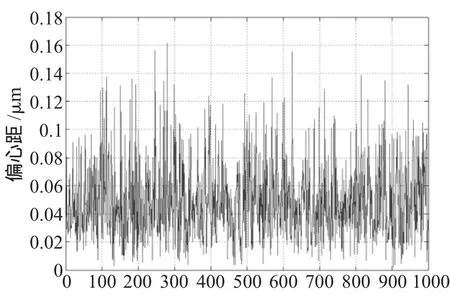
图4 偏心数据分析

从图中可以看出偏心距大部分在0.02μm到0.1μm之间变动，最大接近0.16μm，3σ值为0.15μm左右。

4 缺口偏向

质心法：公式为：

其中，N为有效采样计算点数，θi为第i次采样点的转台角度值，θi+1为第i+1个采样点的转台角度值，ri为第i次采样的硅片半径值，ri+1为第i+1次采样的硅片半径值，150为硅片实际半径。

仿真1000次，偏向数据如图5所示。

从图中可以看出偏向误差大部分在1μrad到25μrad之间变动，最大接近25μrad。

最小二乘法：

图5 质心法偏向数据分析

公式同形心计算的最小二乘法。仿真1000次，偏向数据如图6所示。

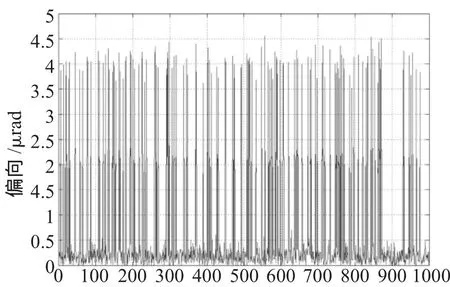
图6 最小二乘法偏向数据分析

从图中可以看出偏向误差大部分在0.05μrad到4.5μrad之间变动，最大接近4.5μrad。

比较两种方法最小二乘法精度最高。

平均最小二乘法：从图11中可以看出有一部分误差数据很小（小于1μrad），而另一部分误差数据相对较大（大于1μrad），由计算得知较大部分误差数据大约占总数据的15%左右，而且这些误差数据的精确范围在3.5μrad到4.5μrad之间。

经计算分析得知，在假设条件下，缺口端点查找准确（缺口数据严格对称时），偏向误差都在1μrad以下，而查找到的缺口端点与实际准确的缺口端点每相差一个点时，偏向误差就会偏差1μrad左右。由于检测缺口使用间隔差分法间隔4个点，缺口端点有时会相差4个点，所以偏向误差有时会偏差4μrad左右。

为消除这种影响，可连续采样几次到几十次，然后计算每次得到的偏向误差平均值，可以提高精度，但这样会增加算法的复杂性。

每次计算误差连续采样5次，然后计算偏向误差平均值，一共仿真1 000次，数据如图7所示。

图7 最小二乘法（采样5次取平均值），仿真1 000次

从图中可以看出缺口偏向误差大部分都在2μrad以下，3σ值为1.8μrad左右。每次计算误差连续采样7次，然后计算偏向误差平均值，一共仿真1 000次，数据如图8所示。

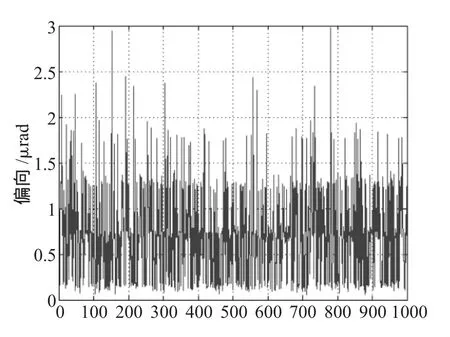
图8 最小二乘法（采样7次取平均值），仿真1 000次

从图中可以看出缺口偏向误差大部分都在2μrad以下，3σ值为1.5μrad左右。每次计算误差连续采样10次，然后计算偏向误差平均值，一共仿真1 000次，数据如图9所示。

从图中可以看出缺口偏向误差大部分都在1.5μrad以下，3σ值为1.2μrad左右。

由图7、8和9中可以看出随着平均次数的增加，偏向误差和3σ值都在减小，所以想要继续降低误差只要使平均次数增加即可，但是这样会增加时间复杂性。

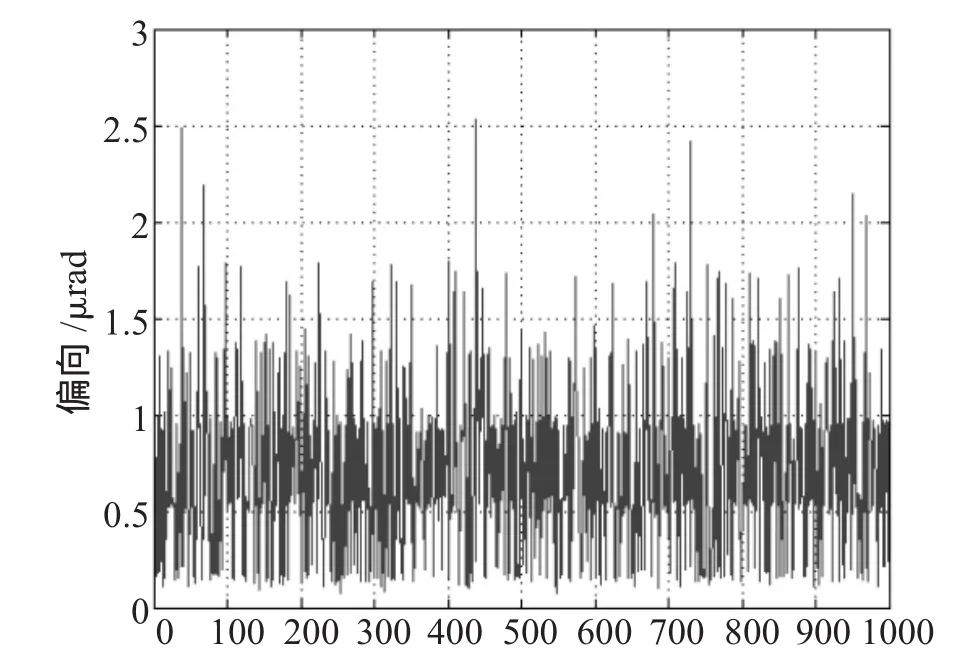
图9 最小二乘法（采样10次取平均值），仿真1 000次

5 结 论

因为预对准精度要求为：上片偏心：500μm；定心窗口：最小为±20μm；定向精度：±30μrad；完成预对准所需的时间：≤20 s。对比以上算法，缺口检测采用差分发、定向采用质心法最终可达到以上精度要求并且预对准时间≤15 s提高了产率。

[1](美)莱(Lay，D.C.)著，刘深泉译.线性代数及其应用[M].北京：机械工业出版社，2005.

[2]张韵华.数值计算方法与算法[M].北京：科学出版社，2006.

[3]周杰，韩龙.采用线阵光学传感器的晶圆预对准方法[J].黑龙江科技学院报，2009.6.