基于Mallat算法的动弹性模量测量研究*
2011-06-03刘瑞安
王 磊,刘瑞安
(天津师范大学 物理与电子信息学院,天津 300387)
动弹性模量 (Dynamic Young's Modulus)是建筑工程设计中混凝土等刚性材料的力学性能的一个重要参数,反映了某段时间内材料在外力作用下的细微形变,因此动弹性模量的测量在建筑工程的质量监控与评估中有着重要的意义。混凝土的弹性模量是频率的单值函数,该函数的关键变量是混凝土试件的共振频率,即由试件的谐振频率,可推算出其强度来。由此,混凝土的强度测量可以简化为先进行动弹谐振频率测量,再计算动弹性模量的过程[1]。
当前刚性材料的动弹性模量测量方法有扫频法、快速傅里叶变换法(FFT)等。在扫频法中,先由激振器从低频到高频依次发射振动波到待测试件表面,迫使其产生非平稳、瞬态的反馈振动波形,通过不同频率间反馈波形幅值的比较,扫描出谐振频率点。而FFT法是在数字电路快速发展的背景下,由数字处理器对反馈波形进行快速离散傅里叶变换,计算出功率谱中的峰值频率作为谐振频率。在FFT算法中,消除了扫频法中激振器在不同频率下激振波振幅的误差影响。而FFT算法在有限的采样点下,其低频精度较低(频谱范围为 20 kHz时,误差在±20 Hz以上)。为此,本文将小波变换中的多分辨分析方法引入到动弹性模量的测量中来,可在现有传感器硬件电路基础上,通过在DSP平台上的Mallat算法实现高精度的频谱计算,提高谐振频率测量精度,消除因传感器不一致所导致的误差影响,从而提高动弹性模量测量的准确度。
1 Mallat算法的频谱分析原理
1.1 Mallat算法原理及分解过程
Mallat算法是小波信号处理中最常用的小波快速算法。连续小波变换是指:把某一被称为基本小波(亦称母小波或基波)的函数Ψ(t)作位移τ后,在不同尺度α下再与待分析信号 x(t)作内积[2]。

Mallat算法主要是用基于多分辨分析的多采样滤波器组来分解信号,可以把信号分解为离散平滑分量和离散细节分量。这些离散分量间的关系可用滤波器组的形式表现。Mallat算法的小波分解公式:

其中k=0,1,2,…,N-1,N表示输入采样序列的个数;和分别是第j级小波分解后的低频平滑分量与高频细节分量;j的最大值为log2N,j=0时,是原始输入信号的离散序列;hk-2n是多分辨分析的尺度系数;gk-2n是多分辨分析的小波系数。从滤波器角度理解,尺度系数与小波系数可分别视作分解过程中的低通滤波器系数和高通滤波器系数[3]。

式(4)中,f(l)是滤波器系数,无论是低频系数Lo_D还是高频系数Hi_D,都需从其第1个数开始计算,即l从0开始,其范围是l=0,1,2,…,lmax。由此,离散小波分解过程可简化为:

1.2 Mallat算法的波形重构及频谱细化
重构算法是分解算法的反演,以得到特定频域段的低频系数,其利用相邻两级的低频与高频系数复原出上一级信号。离散小波算法的重构公式为:

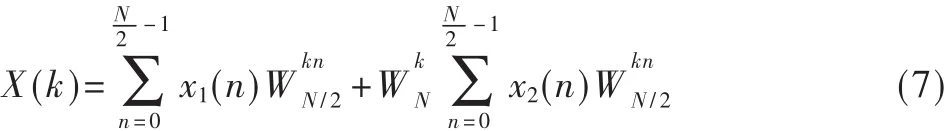
其中x1(n)和x2(n)分别为波形信号x(n)的偶数序列与奇数序列,WN=,k=0,1,2,…,N-1。
对不同尺度下的波形信号进行重采样和离散傅里叶变换后得到的频谱,再经过组合叠加即是所求的细化后的频谱。
2 动弹性模量测量原理
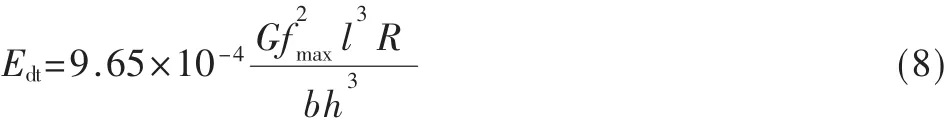
上式中,Edt为横向动弹性模量,单位为 Pa;G是试件质量,单位为 kg;fmax是在外力作用下试件谐振时的峰值频率;l、b、h分别对应试件的长、宽和高,单位为 mm;R是取决于试件边长及泊松比的修正系数,对于l/h=4、泊松比大约为1/6的混凝土试件,R取1.5。在混凝土等硬质材料的动弹性模量的测量中,当温度与湿度等外界环境因素稳定时,式(8)中其他变量的测量误差较小,难点是非平稳状态的测试波形的频谱计算。每个试件因为结构的差异及缝隙的存在,其共振频率都有若干个,称其为共振频率带,在力学测量中,建筑力学设计中的动弹性模量测试只研究其低频段(≤20 kHz)内的共振频率。
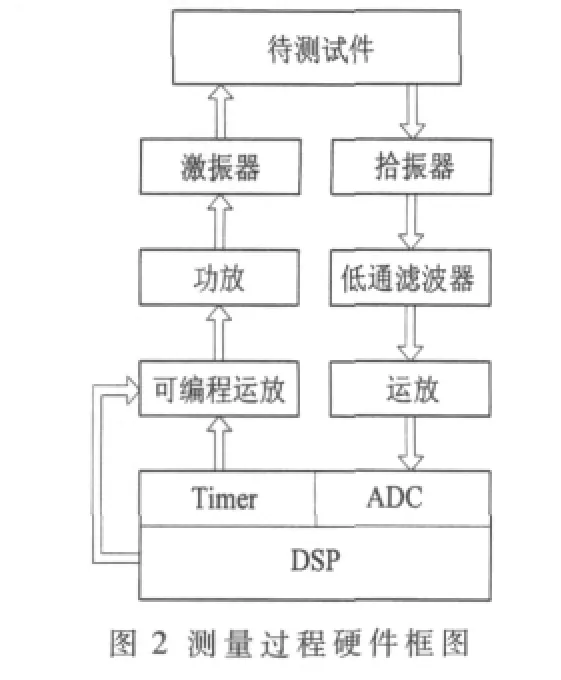
测量过程硬件框图如图2所示,激振器由密封在钢制圆柱体内腔的大功率动圈扬声器构成,垂直安装在扬声器锥盆上的铝制测杆伸出腔外3 mm。拾振器构造与激振器类似,但扬声器由灵敏度较高的压电陶瓷片替换。在测量前,首先将激振器正对混凝土试件侧面的中心位置,拾振器则放置在试件同一面的侧边沿,保持激振器和拾振器的测杆都轻轻地接触在混凝土试件表面上(测杆与试件的接触面涂抹一薄层耦合介质)。
测量过程中,首先由DSP调制出PWM信号,通过可编程运放(PGA)调整波形幅度后,再经功放电路功率放
根据胡克定律(Hooke's law)定义:材料在弹性形变范围内,力与形变成正比,其比例系数称为弹性模量,而根据测试方向分为横向动弹性模量和纵向动弹性模量。在建筑工程中,混凝土的弹性模量测试以横向外力作用测试为主,简称为横向动弹性模量,下面列出了横向动弹性模量计算式:大后连接到激振器的正负极。激振器的测杆将激励信号施加到混凝土试件中间点,试件在外力作用下振动。由于压电效应,拾振器中的压电陶瓷片将试件因受迫振动而产生的机械波转换为电压信号(Vp-p<1 mV),该非平稳电压信号经低通滤波器滤除高频干扰后送至由LM833构成的单端运放电路放大1 000倍,其滤波放大电路如图3所示。

放大的电压信号接入DSP的ADCINA0管脚,DSP以固定的采样频率对该电压信号进行模数转换,所得的数组x(n)作为Mallat算法的原始处理数据源(每次算法的采样点数N=1 024)。当激励源的激励频率接近于试件的固有频率时,产生共振效应,试件强迫振动的振幅及功率达到最大,通过算法计算出的峰值频率fmax作为试件的共振频率。
3 Mallat算法测量谐振频率过程分析
3.1 DSP中Mallat算法的程序设计方法
在动弹性模量测量中,Mallat算法是基于TMS320F2808型32位定点数字信号处理器(DSP)平台实现的。基于哈佛总线结构的F2808型DSP最高运算速度为100 MIPS,其内置的12位ADC模块最小转换时间为160 ns。针对刚性材料的共振频率低频段分布的特点,由Nyquist抽样定理可知模数转换单元的最小采样频率为40 kHz,但为了减小能量泄漏及幅值失真,采样频率fs设定为采样点数N的整数倍,即fs=40.96 kHz。
程序中设置16位的ePWM模块作为激振器的信号源:首先将来自系统的时钟信号通过PLL(锁相环)预分频到10 kHz,修改周期寄存器TyPR以改变输出PWM方波的频率。
在DSP程序设计中,为了提高系统运算效率,Mallat算法操作通过C语言嵌套汇编语言实现:在C函数的框架中,汇编语句通过动态参数传递的形式进行调用,并且对相应C语句进行优化,以减少函数的调用次数。DSP中,当RPT流水线启动后,通过循环寻址指令间接地在RAM空间构造的循环缓存区中调用采样序列x(n),DSP可在单指令周期内通过硬件乘法器实现快速乘加操作,以便迅速完成卷积、滤波等小波运算。
波形信号分解过程中,根据采样数组x(n),针对式(5)中的n,从尺度n=1开始循环计算,求出滤波器系数与剩余系数的加权和,分别得到和。当滤波器系数序列与x(n)作乘法运算时,各个系数依次相乘然后累加即为的值。依次循环,再将滤波器系数序列向右移两位,再与输入信号相乘。最后剩下两个值时再从第一个位置继续,从而构成循环,得到最后的与。最终获得不同尺度下的分解波形信号[5]。
对小波分解出的低频波形信号再重采样后,为减小系统程序开发难度,DSP调用TI提供的FFT库进行1 024点的FFT变换,以进行频谱计算操作。
3.2 频谱细化中频率混淆的改进
由于小波实际滤波器的非理想截止特征,信号卷积后各频带混入了相邻频带成分,且各尺度的隔点采样不满足采样定理,Mallat算法进行频谱计算过程易产生频率混淆。
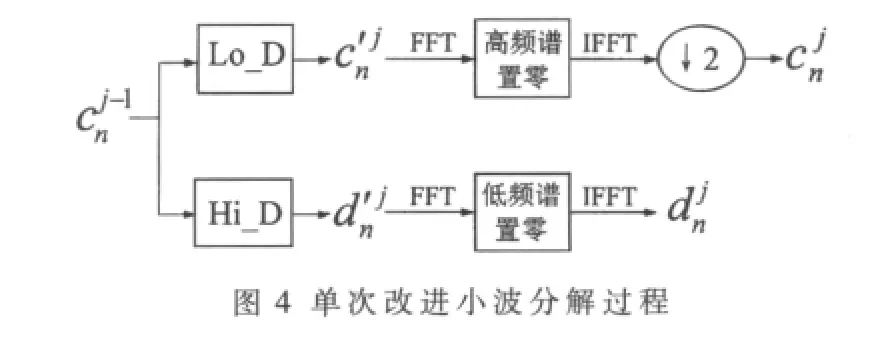
为此在重建过程中,DSP程序中引入了单子带重构改进算法,即利用FFT和 IFFT(快速傅里叶逆变换)消除各重构后的子带信号中多余的频率成分,以最终消除频率混淆。对于小波分解出的信号,在以fs/2j+1为对称中心,半径小于fs/2j+1的频率范围内,会因频谱折迭而造成虚假频率成分。以消除取得过程中的频率混淆为例进行说明:对与hk-2n卷积后的结果先 进 行 FFT,对FFT结果中频率大于fs/2j+1部分的谱值置零,再对置零后的结果进行IFFT,最后对IFFT的结果进行隔点采样,将采样后的结果作为真正的作进一步分解[6]。图 4为改进后的分解过程图。
4 试验分析及结果
为验证测试系统中算法的精确度,在试验电路中:DSP的 PWM周期定时器设定值 FT从 50 Hz~1 kHz范围内以 0.25 Hz/ms增加,当 FT达到 1 kHz后,以 1 Hz/ms增加到5 kHz为止;为了减小激振器中电磁线圈的温漂,将PWM的脉宽调制为0.3,激振器输出平均功率PT=5 W;功率谱计算时间平均为3.2 ms;图5是标准试件频谱图的打印输出结果。
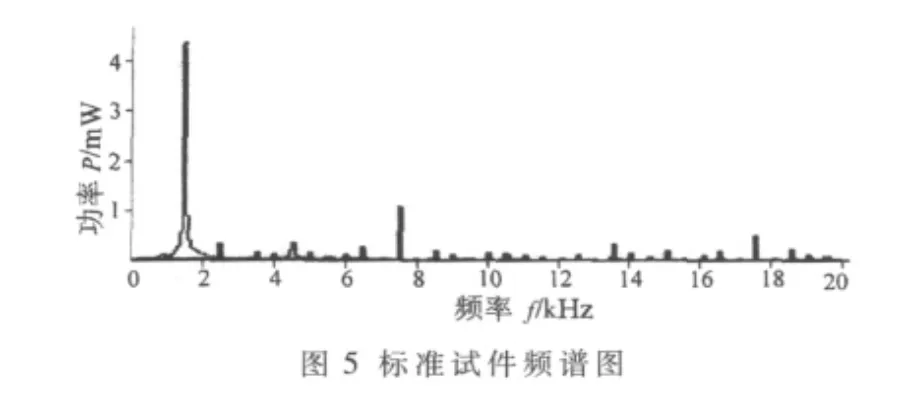
由图5可知,峰值频率fmax=1.502 kHz,即该试件的谐振频率为1.502 kHz,符合一般情况下混凝土的谐振频率分布。对于l=400 mm、b=h=100 mm的标准试件,当其质量G=10.0 kg时,由式(8)计算出动弹性模量Edt为 20.90 GPa。
由于通常制备的混凝土试件的共振频率分布不均匀且难以预测[7]。试验中,为了测试系统的计量准确度,使用了函数信号发生器来模拟激振波形:信号源输出不同中心频率下峰值为0.5 mV的sinx/x周期函数波形,利用DSP硬件平台测试FFT算法与Mallat算法在同样采样点数下的谐振频率测量的相对误差,结果如表1所示。
由表1可知,测试平台在20 kHz量程时,FFT算法的低频段相对误差较大,在高频段与Mallat算法相同,而Mallat算法测量频谱的相对误差始终小于0.3%。所以,两种算法相对于量程的精度相同,而由于Mallat算法的多尺度分析等特点,其在低频段内谐振频率测量值的可信度更高,相对于常规FFT算法有效提高了动弹性模量的测量精度。
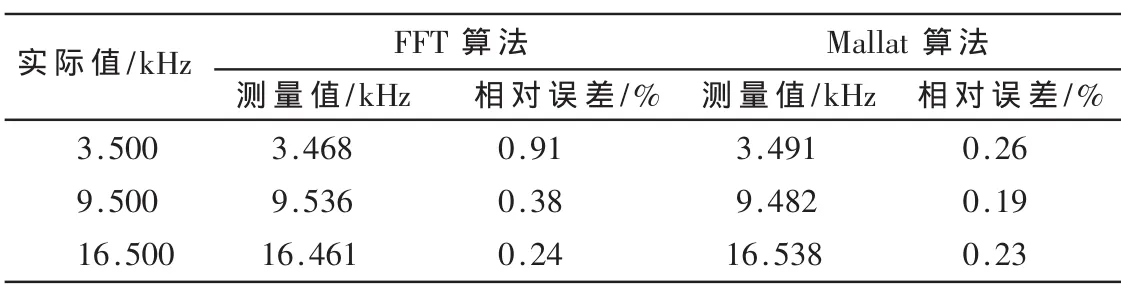
表1 20 kHz范围的FFT与Mallat算法比较
本文通过在DSP平台上实现Mallat算法,运用离散小波变换的多分辨率分析方法对非平稳的谐振波形进行频谱分析。利用其多尺度测量由粗至细提取出激振信号的局部频域特征,再通过小波改进算法去除频率混淆,可快速准确地扫描出其中的功率峰值点以作混凝土等刚性材料的动弹性模量计算。
通过Mallat算法的多分辨率分析方法,保证了测试系统在20 kHz量程内相对误差小于0.3%,重复性误差小于0.5%,满足了建筑工程设计中混凝土动弹性模量测量的精度需求。在利用Mallat算法研究声信号频谱的基础上,可通过超声波定位精度高、穿透能力强等特点来进行混凝土结构件的探伤定位等无损检测研究。
[1]刘飞,王海飚,翁丽娅,等.基于小波理论对混凝土损伤特性的试验研究[J].岩土力学与工程学报,2005,24(14):2581-2587.
[2]杨福生.小波变换的工程分析与应用[M].北京:科学出版社,2001:58-72.
[3]MALLAT S.信号处理的小波导引[M].北京:机械工业出版社,2002:388-397.
[4]侯正信,王成优,杨爱萍.有限长度信号 Mallat算法的边界延拓方法[J].数据采集与处理,2009,24(6):714-720.
[5]PATIL S,ABEL E W.Real time continuous wavelet transform implementation on a DSP processor[J].Journal of Medical Engineering&Technology,2009,33(3):223-231.
[6]封常生.小波分析在信号处理中的应用[D].上海:上海交通大学,2007.34-50.
[7]SUZUKI T,OHTSU M et al.Relative damage evaluation of concrete in a road bridge by AE rate-process analysis[J].Materials and Structures,2006,40(2):221-227.
