防空导弹可靠性增长试验加速方法的工程探索

张绍伟，史松伟，张昶，王晓枫

（上海机电工程研究所，上海 200233）

1 引言

可靠性是防空导弹的一项重要的性能指标，对武器装备的战备完好性起到非常关键的作用。在当前防空导弹型号研制过程中，通常都通过常规可靠性试验的方法对导弹全弹、弹上整机的可靠性进行摸底、增长和验证，这些工作对实现导弹可靠性要求起到了非常重要的作用，也取得了良好的效果。

防空导弹的可靠性指标一般以飞行可靠度为主。在实际型号的研制过程中，对弹上机电类整机，把飞行可靠度的要求按指数寿命分布模型转换为平均故障间隔时间（MTBF）形式的指标，以便于开展可靠性的设计和验证。对于空空导弹还有挂机飞行可靠性的要求，挂机飞行可靠性的指标通常是以挂机飞行MTBF的形式提出。因此，防空导弹的可靠性增长试验可以采用GJB1407《可靠性增长试验》规定的增长试验方案来开展试验。试验剖面一般是按GJB899《可靠性鉴定与验收试验》提供的剖面。

近年来，随着防空导弹设计水平的不断发展，使用方对防空导弹的可靠性提出了越来越高的要求。飞行可靠度的要求越来越高，而且作战距离的要求也越来越大，飞行任务时间的提高，使得飞行MTBF指标要求大幅度地提高。空空导弹可靠性指标要求的提高还体现在挂机飞行可靠性指标方面。弹上设备的MTBF指标往往可达数千小时。可靠性指标的提高对可靠性增长试验方法提出了新的课题，由于指标的提高，常规可靠性试验的效率又很低，使得可靠性增长试验时间不断延长，常常会影响研制的进度。可靠性发展趋势要求必须研究可靠性增长试验的工程方法来缩短试验总时间。

2 防空导弹可靠性增长试验工程方法分析

高可靠性产品的可靠性增长试验方法研究的目的是缩短试验时间，提高试验效率。一般来说，缩短可靠性增长试验时间可从3方面入手。一方面是增加受试产品的数量。防空导弹机电产品的工作状态的寿命分布模型通常认为是服从指数分布，所以试验总时间是所有受试产品试验时间的累积，增加受试产品数量就可以获得足够的试验总时间。但对于防空导弹全弹或者弹上整机来说，由于成本的限制，不可能投入多件产品进行试验，大多数情况下只能投入1～2件产品。所以依靠样机的投入来缩短试验时间工程上是不合适的。另一方面是更改可靠性增长试验的增长模型。按GJB1407的规定，可靠性增长试验的模型可选择杜安模型或者AMSAA模型。按这两种增长模型来开展试验，如果要达到比较好的试验效果，则试验总时间通常为产品MTBF目标值的5～25倍，所以，如果采用这种方法进行可靠性增长，试验总时间就是不可接受的。在航天行业标准QJ3127《航天产品可靠性增长试验指南》中，提供了一种指数寿命分布的截尾试验方法，按照指数模型，选择合适的置信度，以产品出现零故障为条件制定统计试验方案。这种方法的试验总时间很短，因此适合在工程上的应用。

采用加速应力的试验剖面是缩短可靠性试验时间的最好方法，可以极大地缩短试验时间，一般情况下可以使试验总时间缩短为原来的数十倍。但加速试验的关键是能够获得加速应力与正常应力下可靠性的定量关系。

3 防空导弹可靠性增长试验的加速方法

研究可靠性增长试验的加速试验方法，最关键的内容是选择加速的应力类型和加速模型。防空导弹可靠性试验一般采用3种环境应力（温度、湿度和振动）的综合条件。湿度应力一般不适合作为加速应力施加，所以在加速试验应力的选择上，应该考虑采用温度应力、振动应力，或者温度-振动的综合应力。

以温度作为加速应力可采用阿伦尼斯（Arrhenius） 模型：

式（1）中：ξ——某寿命特征，如中位寿命、平均寿命等；

A——常数，且A>0；

E——激活能，与材料有关，单位是电子伏特；

K——波尔兹曼常数，为8.617×10-5eV/℃；

T——绝对温度。

上述模型可以用对数形式表示：

其中a=1nA，b=E/K。

加速系数的计算模型如下：

设某产品在正常应力水平S0下的失效分布函数为F0（t），tp,0为其p分位寿命，即F0（tp,0）=P。又设加速应力水平Si下的失效分布函数为Fi（t），tp,i为其p分位寿命，即Fi（tp,i）=P，则两个p分位寿命之比：

被称为加速应力水平对正常应力水平的p分位寿命加速系数或加速因子。

从加速模型和加速系数的模型可以看出，进行加速试验的核心工作，是获得加速模型中的激活能E参数或者其变形量b的估计值。如果已知加速模型的参数，就可以利用某个高应力水平下的试验数据或可靠性评估值，直接推算在正常应力下的试验数据或者可靠性评估值。所以防空导弹全弹或弹上整机加速试验的核心是获得整机激活能的数值。整机激活能数值的获取，可通过两种途径：利用相似产品的工程经验数值，通过加速试验中多个应力下试验数据进行估计。这两种途径分别对应了两种加速试验的实施方法：预先给定激活能的试验方案，根据经验数据直接给定激活能的数值；预先不给定激活能的数值，通过加速试验中多个应力下的试验数据来进行估计。

根据可靠性增长试验的实施过程分析，如果在试验实施中通过多个应力下的故障数据来估计激活能，那么试验过程将会非常复杂，数据计算的方法统计分析方法也存在一定的困难。而预先给定激活能的数值，也必须有一定的工程基础，通过多个相似产品的试验结果才能给出。国内相似产品（防空导弹、飞航导弹）加速可靠性试验的工程研究情况表明，国内相关产品的试验数据非常少，因此预先给定激活能的方法也存在很大的困难，如果给定的激活能不准确，那么试验结果的可信度是比较低的。

以振动作为加速应力可采用的逆幂律模型：

式（2）中：ξ——某寿命特征，如中位寿命、平均寿命等；

A——常数，且A>0；

c——一个与激活能有关的正常数；

V——应力，常取电压。

上述模型可以用对数形式表示：

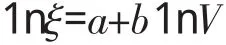
逆幂律模型表示产品的寿命特征是应力V的负数次幂函数。

加速系数的计算模型如下：

设某产品在正常应力水平S0下的失效分布函数为F0（t），tp,0为其p分位寿命，即F0（tp,0）=P。又设加速应力水平Si下的失效分布函数为Fi（t），tp,i为其p分位寿命，即Fi（tp,i）=P，则两个p分位寿命之比：

按照逆幂律模型，可以推导出振动应力作为加速应力的加速系数的公式如下：

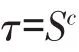
其中S为振动应力比，对于防空导弹可靠性试验中的随机振动应力，其值为加速应力的功率谱密度与非加速应力功率谱密度之比。

这个公式与MIL-STD-810G中给出的、基于疲劳损伤的经验公式一致。在该文献中，同时给出参数c的经验范围：2.5～4。另外，在GJB1032《电子产品环境应力筛选》中，也给出了不同功率谱密度下同样的换算公式，并且参数c取3。由此可知，与温度应力加速的情况相同，使用振动应力作为加速应力的关键问题也是获得激活能的数值，但是，使用振动应力作为加速应力的方法与用温度作为加速应力的方法相比，更成熟，其激活能的数值取值范围也比较确定。国内相似产品也有类似的应用实例。另外防空导弹对振动环境应力比较敏感，所以振动应力加速对导弹弹上产品而言应该效果比较好。

前面分析了温度、振动分别作为加速应力的加速试验方案，在这两种方案下，其它应力以非加速应力的方式施加。在工程实际应用中，还可以考虑把温度和振动两种应力同时作为加速应力施加，这种方式的加速系数将会更高，能够大大提高试验效率。这种试验方案的关键问题也是加速模型。以温度和振动作为加速应力的数学模型主要有广义Eyring模型和温度-非热能（T-NT） 模型。

广义Eyring模型公式为：

用对数形式表示：

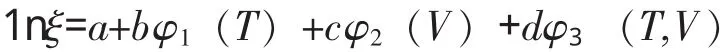
其中a、b、c、d是待定常数。

可以看到，该模型除了包含两种应力单独的函数项，还包含了两种应力共同作用的项，因此加速模型比较复杂，并非是两种应力加速系数的简单叠加。

温度-非热能（T-NT）模型的公式为：

该模型可以用对数形式表示：

其中a、b、c是待定常数。

可以看出，该模型中两种应力不相关，加速寿命为两应力因素的叠加。

对比以上两个模型，可以了解到，前一个模型考虑了两种应力共同作用下的影响，因此可能更接近于实际情况。但由于该模型复杂，在进行数据处理和可靠性评估的时候存在困难，因此在进行导弹加速试验时，可考虑使用T-NT模型，该模型的计算简单，计算加速系数时只需把两项加速系数相乘即可。另外，文献中对双应力加速模型的研究也有一些其它介绍，例如：Barker给出的、基于累积疲劳损伤的模型等。但由于这些模型还没有得到工程上的广泛认可，因此暂不适合在导弹工程研制中采用。

对于两种应力同时加速的方案，国内尚无整机级的试验，有资料显示，在器件级产品中曾开展过航天电连接器综合环境应力加速试验研究。该研究采用温度、振动作为加速应力，通过均匀正交试验设计理论，并用Weibull寿命分布进行了统计分析，采用的加速模型也是前述T-NT模型。

从上述3种加速试验的方法的分析可知，振动应力加速的方式容易实施，而双应力加速的方式效率更高。另一方面，从导弹弹上产品的失效机理方面分析，由于整机产品组成复杂，特别是导弹产品属于机电类产品，对温度和振动敏感的各类故障模式都存在。所以工程上采用双应力的加速试验方案是比较好的方法，不但能提高试验效率，还有利于更多地暴露潜在的故障。

4 工程应用分析

在某电子舱的可靠性增长试验中，对上述加速方法进行了初步的尝试。该产品的MTBF指标较高，在制定可靠性增长试验方案时，采用了加速应力，并借鉴了QJ3127中指数模型截尾试验方案来确定增长试验的总时间。可靠性加速试验剖面依导弹环境条件，同时参考了GJB899中相关规定制定温度、湿度、振动的综合环境试验条件。为模拟导弹可能遇到的冷天、热天、标准天气象环境，试验每个循环选择两个典型温度条件进行模拟，并在其中的冷天和热天阶段安排极冷和极热温度。在每个循环中安排2次热天、2次冷天、2次标准天。以冷天-热天-热天-冷天的顺序施加。

加速应力选取随机振动应力，温度和湿度作为非加速应力同时施加。振动应力的加速模型按逆幂律模型。试验仅选择一个应力水平进行试验。采取预先设定参数C的量值为3，振动量级为原量级的2倍。为提高试验效率，在试验中还把标准天温度条件适当地加严，改为热天的温度。

试验的可靠性评估使用指数模型的经典法方法进行评估：

式（3）中：C——置信度；

T——总试验时间；

r——责任故障数；

θL——MTBF置信下限；

产品按试验方案进行了试验，达到规定的总试验时间时截止。试验期间共发现两个故障，一个故障是电子部件失效，另一个故障是结构失效。对结果的评估表明该产品的可靠性达到了要求，但由于本试验是增长性质的试验，虽然产品通过了试验，但没有达到暴露较多潜在缺陷的目的。这表明仅以振动一种应力作为加速应力，实际上对在综合环境应力下使用的导弹效果不是特别明显，可能会过高地估计产品的实际可靠性水平。本次试验在一定程度上说明了导弹可靠性增长试验应该进一步研究采用温度-振动联合应力进行加速的方法。

5 结束语

加速可靠性试验是产品开展可靠性试验的一个重要方法，在加速可靠性试验方法的研究方面，国外起步较早，工程应用也很多，国内武器装备研制的工程中也开展了大量的研究，但对于整机级产品如何开展加速试验，还没有形成明确的结论，主要原因是整机的加速试验模型和统计评估方法上还存在难点，在整机和全弹产品级别开展的试验目前还没有非常成功的案例。本文所介绍的试验是对加速方法的一个探索性的尝试，为后期进一步开展研究积累了经验。

[1]茆诗松，冯银才，王玲玲，等.可靠性统计[J].北京：高等教育出版社，2008.