复合式路面层间剪应力分析

袁 明，凌天清，张睿卓，房 刚

（重庆交通大学土木建筑学院，重庆 400074）

复合式路面层间剪应力分析

袁 明，凌天清，张睿卓，房 刚

（重庆交通大学土木建筑学院，重庆 400074）

复合式路面的常见病害常表现为层间剪切滑移破坏。选取典型的水泥混凝土下面层、黏结层、沥青混凝土上面层为一整体，应用BISAR3.0程序，计算分析了复合式路面层间最大剪应力、剪切角及其对温度、结构层厚度、材料模量、行车荷载等参数的敏感性。结果表明:AC层厚度、黏结层模量、行车荷载对层间剪应力、剪切角影响显著，当黏结层厚度由6 mm变为16 mm时，层间最大剪应力降低48.85%，剪切角降低11.29%;同时，综合分析黏结层厚度对层间剪应力、层间抗拉拔性能的影响，确定黏结层的合理厚度约为3 mm。应用MATLAB软件surf、fminsearch工具绘出层间剪应力、剪切角分别与AC层厚度、黏结层模量的三维曲面图，并进行非线性优化拟合出3者之间的函数关系。

道路工程;复合式路面;剪应力;剪切角;非线性优化

在水泥混凝土路面上加铺沥青层，即修筑水泥混凝土与沥青混凝土（PCC-AC）复合式路面结构，不仅可减少沥青用量（与柔性路面相比），又可弥补刚性路面的不足［1］。但复合式路面本身也存在着薄弱环节，由于上面层沥青混凝土与下面层水泥混凝土分层铺筑、模量相差悬殊、变形协调性较差，尤其在高温、超载重载车辆作用下，复合式路面AC、PCC层间很容易发生剪切滑移破坏，因此黏结层材料的选择与设置对于改善复合式路面的抗剪性能、提高其使用寿命具有重要的意义。文献［1］详细阐述了复合式路面的结构设计理论、应力分析的方法和施工技术。徐勤武，等［2］通过三维有限元模型分析在行车荷载作用下，层间产生的剪切应力及张拉应力，结果表明:层间摩擦系数为0.5时，层间剪切强度较大同时剪切应力较小。王火明，等［3］分析了界面处理方式、防水黏结材料、界面层沥青用量对界面层强度的影响，斜剪试验角度一律采用45°。顾兴宇，等［4］采用25～65°变角度室内斜剪试验，研究了不同剪切角度下黏结层抗剪强度随温度变化的规律。A.C.Collop，等［5］应用 Leutner试验分析了沥青层间的抗剪特性。层间使用聚酯土工布作为黏结层，最佳的黏层油的用量为0.35～0.50 kg/m2，具体用量依赖于土工材料的类型［6］。国内很多学者对复合式路面的受力特点、黏结性能也进行了深入研究［7-9］。复合式路面层间最大剪应力，尤其是室内剪切试验的剪切角度一直没有明确的理论来确定，笔者基于弹性层状体系理论，应用BISAR3.0程序分析了AC、PCC层间最大剪应力、剪切角及其变化规律;采用MATLAB软件［10］进行非线性优化拟合出层间最大剪应力、剪切角度与其显著影响因素AC层厚度、黏结层模量的三维函数，应用此函数可方便快捷的计算剪应力、剪切角，为提高AC、PCC层间抗剪能力提供理论指导。

1 基本结构计算参数的确定

采用 AC/PCC三维计算模型（图 1），应用BISAR3.0程序进行计算分析荷载作用下复合式路面沥青混凝土层与水泥混凝土层之间的剪应力、剪切角。假设路面结构层间均完全连续，沥青面层和水泥混凝土底面层是均匀的、各向同性的完全弹性材料，路面结构各层四周水平位移为0，不计结构自重;行车荷载取标准轴载，即单轴双轮组100 kN垂直均布荷载，轮压半径δ为10.65 cm，水平荷载按紧急刹车状态计算，路面结构参数见表1。

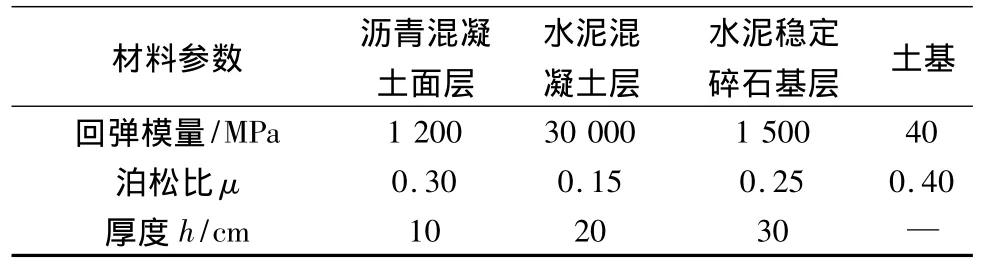
表1 结构层材料参数Table 1 Material parameters of structure layer

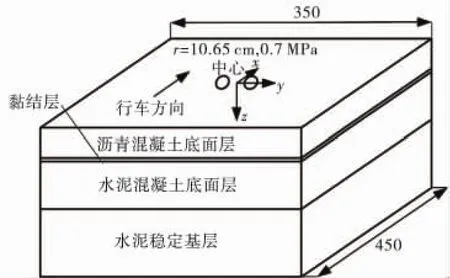
图1 计算模型示意图（单位:cm）Fig.1 Schematic diagram of calculation model

坐标原点设在双圆荷载中间，x轴向与汽车行驶方向一致，y方向为路面横向，z轴向竖直向下。经计算，完全结合状态下层间最大剪应力发生在x方向 9.585 cm，y方向15.975 cm 处，如图2、图3。

2 层间应力计算分析

基本约定:AC表示沥青混凝土层;PCC表示水泥混凝土层;M表示黏结层;AC-M表示沥青混凝土和黏结层层间;PCC-M表示水泥混凝土和黏结层层间;τmax表示最大剪应力;剪切角θ。

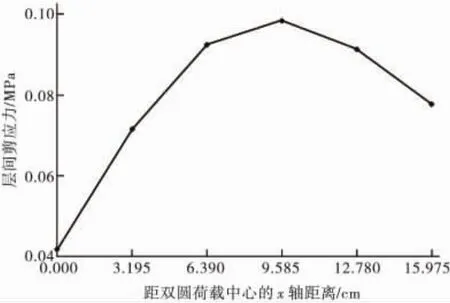
图2 层间最大剪应力的x位置Fig.2 The x position of interlayer maximum shear stress

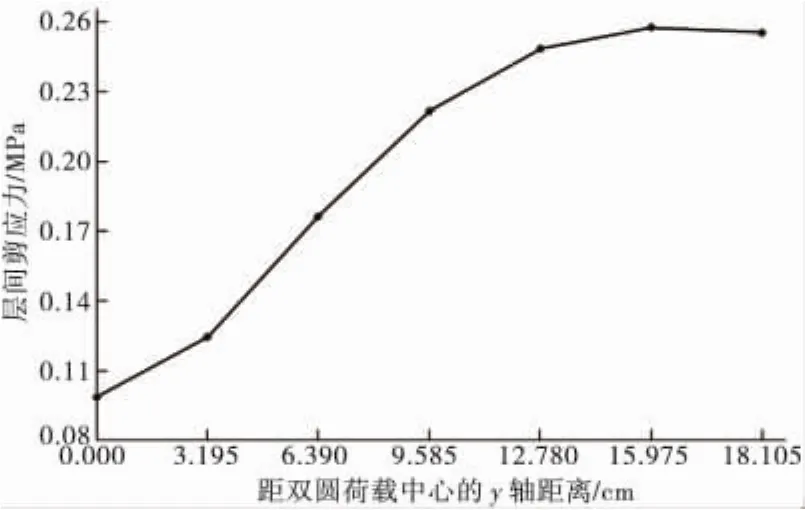
图3 层间最大剪应力的y位置Fig.3 The y position of interlayer maximum shear stress

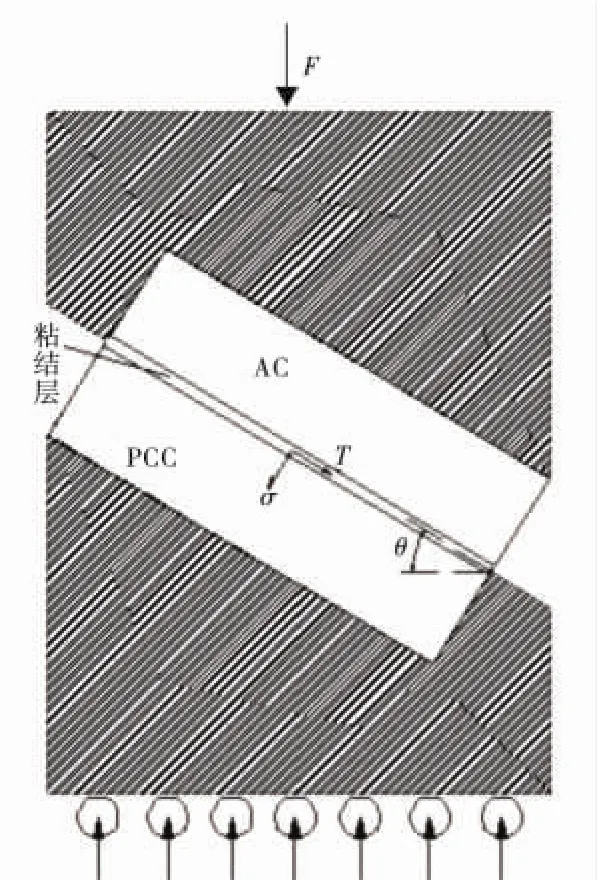
图4 斜剪试验Fig.4 The scheme of inclined shear test

2.1 沥青混凝土层模量的影响

外界气温和荷载作用时间的变化对沥青混凝土模量影响很大，温度愈高，沥青愈软，沥青混凝土模量愈低。控制点为（9.585，15.975），沥青混凝土层厚度取10 cm，沥青混凝土模量分别为 500，1 500，2 500，3 500，4 500 MPa，计算AC层底剪应力及剪切角，结果见表2。

表2 不同沥青混凝土模量对应层底剪应力与剪切角Table 2 Corresponding bottom shear stresses and shear angles of different asphalt concrete modulus

从表2计算知，随着沥青混凝土模量的增大，层间的最大剪应力及剪切角均有所减小，沥青混凝土模量由500MPa变到4 500 MPa，最大剪应力减小6.29%，剪切角几乎不变，沥青混凝土模量对计算结果的影响不大。

2.2 沥青混凝土层厚度的影响

控制点为（9.585，15.975），沥青混凝土层模量保持1 500 MPa不变，改变沥青混凝土层厚度6～16 cm，计算的沥青混凝土层底剪应力与剪切角如表3。

表3 不同沥青混凝土厚度对应层底剪应力与剪切角Table 3 Corresponding bottom shear stresses and shear angles of different asphalt concrete thickness

由表3计算结果可知，随着沥青混凝土层厚度的增大，沥青混凝土层底的最大剪应力和剪切角均有所减小，当厚度从6cm变到16 cm时，层间最大剪应力降低48.85%;剪切角降低11.29%。可见，沥青混凝土层厚度对层间最大剪应力与剪切角影响显著，因此适当提高沥青混凝土层厚度，可以有效降低层间剪应力，减少层间剪切滑移破坏。

2.3 黏结层模量的影响

沥青混凝土模量保持1 500 MPa、厚度保持10 cm不变，黏结层厚度取5 mm不变，首先分析ACM层间（Z=10 cm，取AC层厚度）最大剪应力作用位置是否随黏结层模量的变化而变化，计算结果如图5、图6，AC-M层间最大剪应力依然发生在x方向9.585 cm，y 方向 15.975 cm 处。经计算，PCCM层间层间最大剪应力作用位置亦是此点，此时Z=10.5 cm（AC层厚度+黏结层厚度），分析方法与上述类似，在此不再赘述。

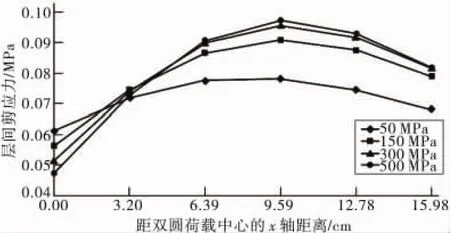
图5 不同黏结层模量下AC－M层间最大剪应力的x位置Fig.5 The x position of AC-M interlayer maximum shear with different modulus of bonding layer

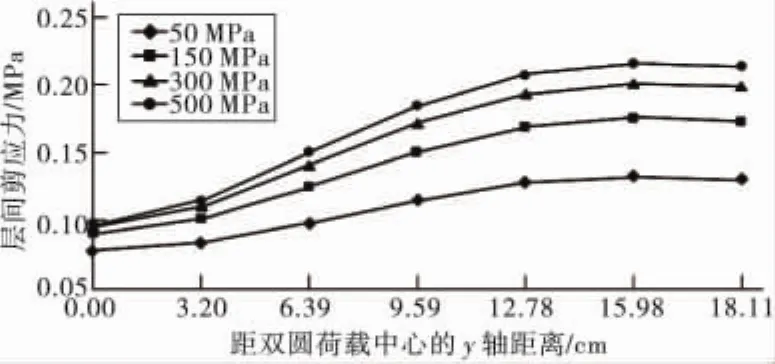
图6 不同黏结层模量下AC－M层间最大剪应力的y位置Fig.6 The y position of AC-M interlayer maximum shear with different modulus of bonding layer

取 x=9.585 cm，y=15.975 cm 为控制点，分析各接触面间最大剪应力、剪切角随着黏结层模量的变化规律。由表4可以看出，当黏结层模量在150，300，500 MPa时，AC-M的τmax相对50 MPa分别增大32.90%，51.97%，63.16%，剪切角相对 50 MPa 分别增大19.08%，31.15%，38.36%;PCC-M 的 τmax相对 50 MPa分别增大 33.24%，52.08%，63.04%，剪切角相对 50 MPa 分别增大19.62%，31.69%，38.90%。表明采用低模量的黏结层可以有效降低层间剪应力、剪切角。

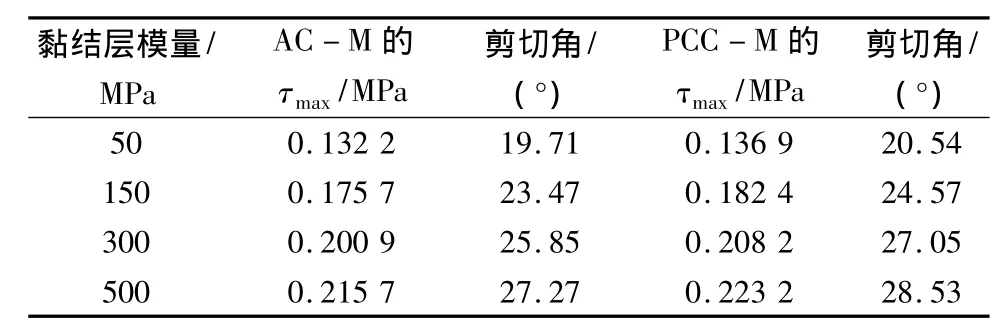
表4 不同黏结层模量对应接触面间最大剪应力与剪切角Table 4 Different bonding layer modulus corresponding with interface maximum shear stress and shear angle

2.4 黏结层厚度的影响

黏结层模量取50 MPa不变，依然首先分析不同的黏结层厚度对AC-M层间、PCC-M层间最大剪应力作用位置的影响规律。计算结果如图7、图8。

1）黏结层厚度为0～6 mm时，AC-M层间最大剪应力依然发生在x方向9.585 cm，y方向15.975 cm处;

2）黏结层厚度为6～12 mm时，AC-M层间最大剪应力发生在x方向6.39 cm，y方向15.975 cm处;

3）黏结层厚度为12～15 mm时，AC-M层间最大剪应力发生在x方向3.20 cm，y方向15.975 cm处。

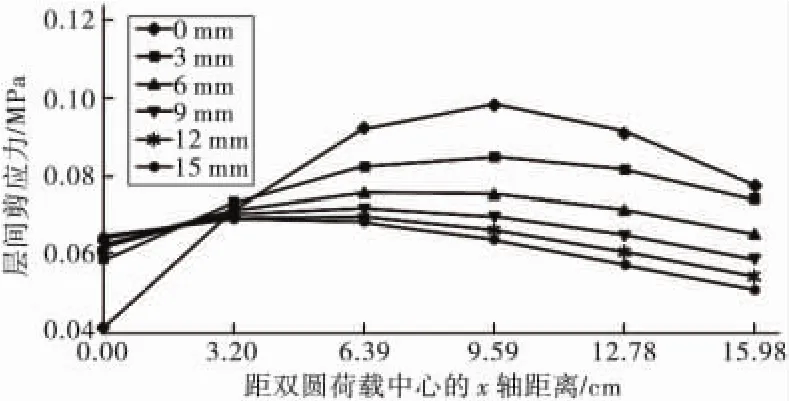
图7 不同黏结层厚度下AC－M层间最大剪应力的x位置Fig.7 The x position of AC-M interlayer maximum shear with different thickness of bonding layer

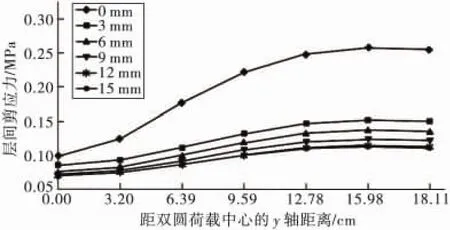
图8 不同黏结层厚度下AC－M层间最大剪应力的y位置Fig.8 The y position of AC-M interlayer maximum shear with different thickness of bonding layer

按黏结层厚度不同，取上述各最大剪应力作用点，分析各接触面间最大剪应力、剪切角随着黏结层厚度的变化规律。如图9，AC-M的τmax、PCC-M的τmax均随黏结层厚度的增大而减小，当黏结层厚度由0增加到3 mm时，层间剪应力减小显著，说明AC与PCC层间设置一定厚度的黏结层是非常必要的，当黏结层厚度继续增大，层间剪应力变化趋势渐缓。

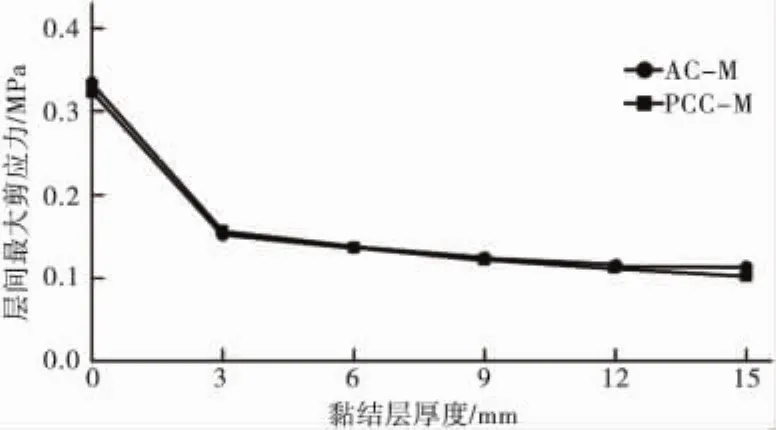
图9 AC－M，PCC－M层间最大剪应力随黏结层厚度变化关系Fig.9 The relationship of AC-M、PCC-M interlayer maximum shear change with thickness of bonding layer

另外，为确定黏结层的合理厚度，还需考虑黏结层厚度与复合式路面层间黏结性能的关系。采用纤维沥青应力吸收黏结层，选取不同的黏结层厚度:1，2，3，4 mm，用环氧树脂黏结胶将夹头黏在试件上，然后放置在温度为（30±2）℃标准试验条件下不少于6 h，使用智能黏结强度仪器进行室内拉拔试验，试验过程如图10，结果如表5。当黏结层厚度为3 mm时，层间抗拉拔能力最强。

图10 拉拔试验过程Fig.10 The process of pull-out test

表5 不同黏结层厚度对应层间黏结强度Table 5 Different thickness of bonding layer corresponding interlayer bond strength

综合分析黏结层厚度对层间剪应力、层间黏结强度的影响，最终选用黏结层的合理厚度为3 mm。

2.5 行车荷载与温度综合作用的影响

如图11、图12，行车荷载相对标准荷载BZZ-100分别超载20%，40%，60%，80%，100%，相应超载系数见表6;水平荷载考虑紧急刹车状态下，仍为垂直荷载的0.5倍。显然，层间最大剪应力与行车荷载成线性比例关系，然而剪切角随着行车荷载的增大，呈一条水平直线，几乎保持19.7°不变，这是由于超载车辆作用于路面上，层间剪应力增大的同时，竖向应力也在同比例增大，因此剪切角近乎为一常数。同时，如文中2.1节所述，外界气温对沥青混凝土模量影响很大，尽管沥青混凝土模量对复合式路面层间剪应力影响不大，但是夏季温度过高会导致层间的抗剪强度明显降低，加上超载重载车辆的作用，很容易发生剪切滑移破坏。

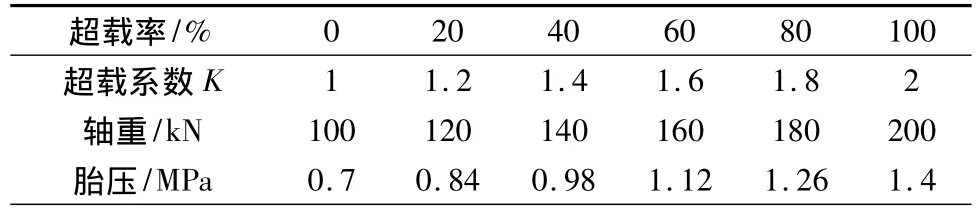
表6 超载参数Table 6 Overload parameters

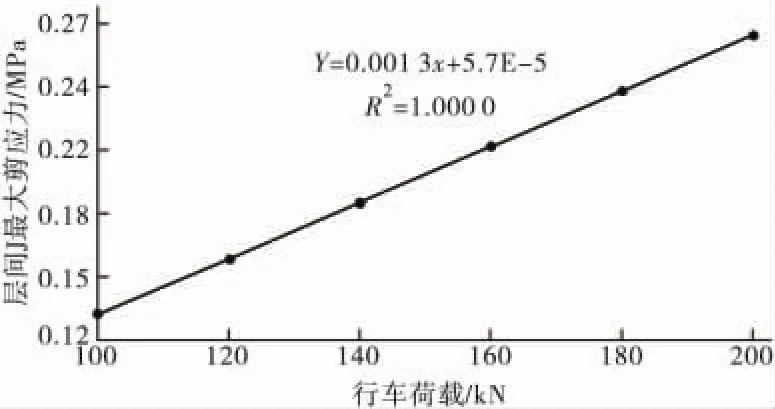
图11 层间最大剪应力随行车荷载变化关系Fig.11 The relationship between inter-laminar maximum shear stress and driving load

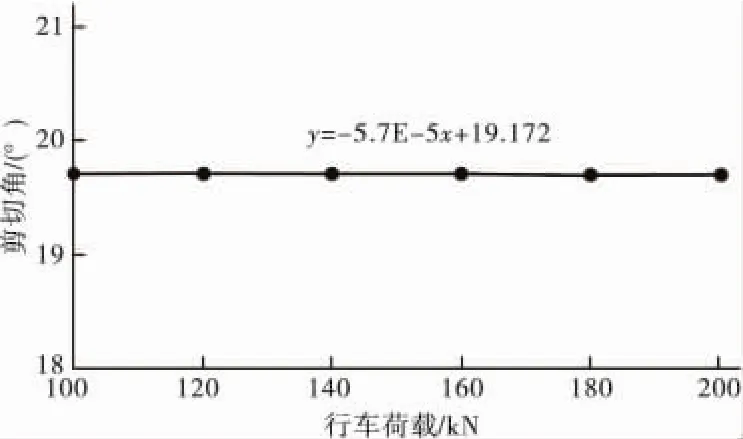
图12 剪切角随行车荷载变化关系Fig.12 The relationship between shear angle and driving load

3 剪切力与剪切角计算方法的提出

综合层间剪应力、剪切角对上述各影响因素（AC层模量、厚度、黏结层模量、厚度和行车荷载）的敏感性高低得知，AC层厚度、黏结层模量、行车荷载影响比较显著。行车荷载取BZZ-100，保持AC层模量为1 500 MPa，黏结层厚度采用合理厚度3 mm，AC层厚度取6～16 cm，黏结层模量分别取50，150，300，500 MPa，计算层间剪应力、剪切角如表 7。

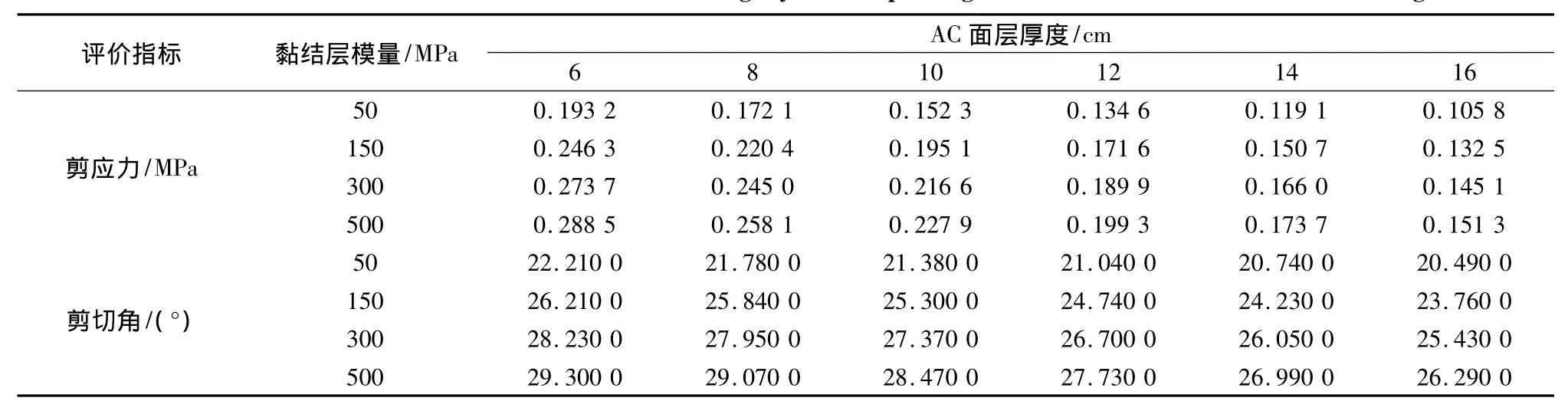
表7 不同AC层厚度、黏结层模量下层间剪应力、剪切角Table 7 Different AC thickness and modulus of bonding layer corresponding with interface shear stress and shear angle

分别提取表7中剪应力、剪切角数据进行整理，应用MATLAB软件中surf程序进行三维绘图，直观地表达出AC层厚度、黏结层模量的变化对层间剪应力、剪切角的影响，如图13、图14。

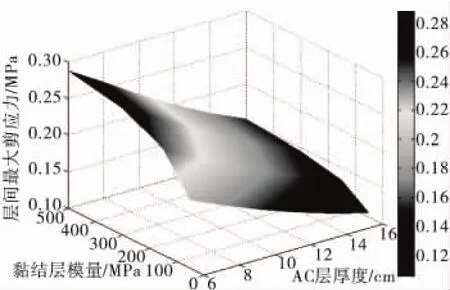
图13 AC层厚度、黏结层模量、剪应力三维曲面Fig.13 3-D surface graph about AC layer thickness，modulus of bonding layer and shear stress

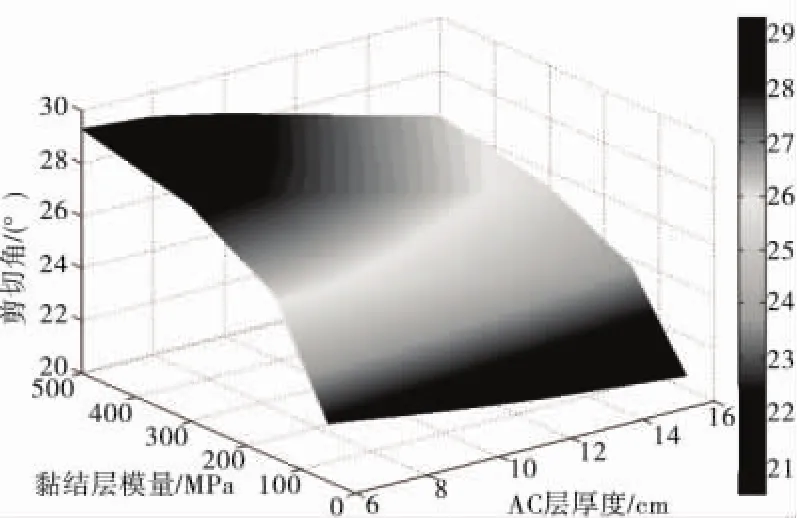
图14 AC层厚度、黏结层模量、剪切角三维曲面Fig.14 3-D surface graph about AC layer thickness，modulus of bonding layer and shear angle

依据表7中数据，应用MATLAB优化工具箱中的fminsearch程序进行无约束非线性最优化，拟合出层间最大剪应力、剪切角分别与AC层厚度、黏结层模量的函数关系:

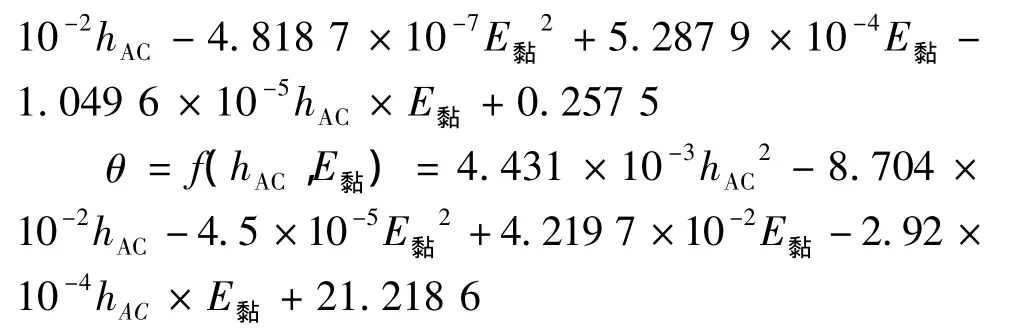
其中:τ为层间剪应力，MPa;θ为剪切角，（°）;hAC为AC层厚度，cm;E黏为黏结层模量，MPa。

误差分析:

1）以hAC=8 cm，E黏=150 MPa为例，查表7可知:此时，τ=0.220 4 MPa，θ=25.84°;经上述函数方程计算得:τ =0.211 9 MPa，θ=25.21°，相对误差分别为 3.86%、2.44%。

2）再以hAC=12 cm，E黏=300 MPa为例，查表7可知:此时，τ =0.018 99 MPa，θ=26.70°;经上述函数方程计算得:τ=0.194 9 MPa，θ=27.09°，相对误差分别为2.63%，1.46%。均满足精度要求小于等于5%。说明上述函数可很好的反映出层间剪应力、剪切角分别与AC层厚度、黏结层模量的关系。

上述公式仅是代表AC层厚度、黏结层模量的影响。由于行车荷载与其他影响因素之间是相互独立的，同时与层间产生的剪应力成线性比例关系（图11），但行车荷载不影响剪切角的大小（图12）。

因此综合上述所有因素，层间最大剪应力τmax综合计算公式如下:

其中:k为超载系数，见表6。

剪切角不随行车荷载变化，计算方法不变。

4 结语

1）笔者计算分析了复合式路面AC-PCC层间最大剪应力、剪切角及其对温度、结构层厚度、材料模量、行车荷载等参数的敏感性，其中，AC层厚度、黏结层模量、行车荷载对层间剪应力、剪切角影响显著。

2）AC层厚度对层间剪应力、剪切角影响明显。当厚度从6 cm变到16 cm时，层间最大剪应力降低48.85%;剪切角降低11.29%，适当提高沥青混凝土层厚度，可以有效降低层间剪应力。

3）当黏结层模量50 MPa增为300 MPa时，AC-M 的 τmax增大 51.97%，剪切角增大 31.15%;PCC-M的τmax增大52.08%，剪切角增大31.69%。因此选择较低模量的黏结层材料，是降低AC-PCC层间剪应力、剪切角的有效措施。

4）黏结层厚度由0 mm增为3 mm，层间剪应力减小明显，继续增大黏结层厚度，层间剪应力依然减小，但趋势明显变缓;同时，通过室内拉拔试验得出，黏结层厚度约为3 mm时，复合式路面层间抗拉拔能力达到最大。综合上述分析，确定黏结层的合理厚度为3 mm。

5）行车荷载对层间最大剪应力有很大的影响，呈线性比例关系，但剪切角几乎保持不变，近似为一水平直线，不受行车荷载影响。因此为减少复合式路面剪切滑移破坏，应加强管理与限制超载、重载车辆的运行。

6）综合上述各种显著影响因素（AC层厚度、黏结层材料模量、行车荷载），应用MATLAB软件优化拟合出复合式路面层间最大剪应力、剪切角的计算公式。

（References）:

［1］ 胡长顺，王秉纲.复合式路面设计原理与施工技术［M］.北京:人民交通出版社，1999.

［2］ XU Qin-wu，ZHOU Qing-hua，Medin C，et al.Experimental and numerical analysis of a waterproofing adhesive layer used on concrete-bridge decks［J］.International Journal of Adhesion＆ Adhesives，2009，29（5）:525-534.

［3］ 王火明，凌天清，肖友高，等.刚柔复合式路面界面层强度特性试验研究［J］.重庆交通大学学报:自然科学版，2009，28（6）:1033-1036.

WANG Huo-ming，LING Tian-qing，XIAO You-gao，et al.Experirnental study on interface loyer strength characteristics of rigidflexible composite pavement［J］.Journal of Chongqing Jiaotong university:Natural Science，2009，28（6）:1033-1036.

［4］ 顾兴宇，王文达.水泥混凝土桥面黏结层抗剪性能要求及简化计算［J］.交通运输工程学报，2010，10（2）:20-25.

GU Xing-yu，WANG Wen-da.Shear property demands of binding layer on concrete bridge pavement and simplified calculation ［J］.Journal of Traffic and Transportation Engineering，2010，10（2）:20-25.

［5］ Collop A C，Sutanto M H，Airey G D，et al.Shear bond strength between asphalt layers for laboratory prepared samples and field cores［J］.Construction and Building Materials，2009，23（6）:2251-2258.

［6］ Barraza D Z，Perez M C，Fresno D C，et al.New procedure for measuring adherence between a geosynthetic material and a bituminous mixture［J］.Geotextiles and Geomembranes，2010，28（5）:483-489.

［7］ 徐勤武，胡长顺，王虎.混凝土桥面复合式铺装层受力分析和设计［J］.长安大学学报:自然科学版，2007，27（4）:28-32.

XU Qin-wu，HU Chang-shun，WANG Hu.Mechanic analysis an design f composite type overlay on concrete bridge pavement［J］.Journal of Chang’an University:Natural Science，2007，27（4）:28-32.

［8］ 倪富健，卢杨，顾兴宇，等.沥青混凝土与连续配筋混凝土复合式路面承载力分析［J］.交通运输工程学报，2007，7（1）:43-48.

NI Fu-jian，LU Yang，GU Xing-yu，et al.Carrying capacity analysis of asphalt concrete and continuously reinforced concrete composite pavement［J］.Journal of Traffic and Transportation Engineering，2007，7（1）:43-48.

［9］ 王涓.水泥混凝土桥面沥青混凝土铺装防水黏结层的性能研究［D］.南京:东南大学，2004.

［10］苏金明，阮沈勇.MATLAB实用教程［M］.北京:电子工业出版社，1998.

Analysis on Inter-laminar Shear Stress of Composite Pavement

YUAN Ming，LING Tian-qing，ZHANG Rui-zhuo，FANG Gang
（School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China）

The common disease of composite pavement is often in the form of interfacial shear slip damage.Firstly，typical cement concrete level layers，bonding layer，asphalt concrete top layer are selected as a whole layer.And then the composite pavement interlayer maximum shear，shear angle and the sensitivity for temperature，structure layer thickness，material modulus，driving load and so on are calculated by using BISAR 3.0 program.Results show that:the thickness of AC layer，the modulus of bonding layer，the traffic load have a significant effect on interlayer shear and shear angle.When the thickness of bonding layer changes from 6mm to 16mm，the interlayer maximum shear reduces by 48.85%，and shear angle reduces by 11.29%.Meanwhile，the influence of the thickness of bonding layer on the inter-laminar shear stress and resistance pull force performance is analyzed compositely，which determines the reasonable thickness of adhesion is 3mm.Surf and fminsearch in MATLAB software are used as tools to draw 3D surface graph about interlayer shear，shear angle with the thickness of AC layer and the modulus of bonding layer;finally，non-linear optimization is carried out to fit out the function of the relationship among the above three.

road engineering;composite pavement;shear stress;shear angle;non-linear optimization

U 416.2

A

1674-0696（2011）06-1318-05

10.3969/j.issn.1674-0696.2011.06.14

2011-04-09;

2011-07-13

袁 明（1986-），男，黑龙江佳木斯人，硕士研究生，主要从事路面结构设计方面的研究。E-mail:yming0809@163.com。