圆形钢筋混凝土桥墩抗震性能（Ⅱ）:试验结果评估

李贵乾，郑 罡，王 军

（1.广西壮族自治区交通规划勘察设计研究院，广西南宁 530011;

2.招商局重庆交通科研设计院有限公司桥梁结构动力学国家重点实验室，重庆 400067;

3.重庆交通大学土木建筑学院，重庆 400074）

圆形钢筋混凝土桥墩抗震性能（Ⅱ）:试验结果评估

李贵乾1，2，郑 罡2，王 军3

（1.广西壮族自治区交通规划勘察设计研究院，广西南宁 530011;

2.招商局重庆交通科研设计院有限公司桥梁结构动力学国家重点实验室，重庆 400067;

3.重庆交通大学土木建筑学院，重庆 400074）

根据桥墩拟静力正交试验现象及数据结果，研究了圆形钢筋混凝土桥墩的变形特征及弯曲强度特性;并对低周反复荷载作用下桥墩的位移延性、等效刚度和刚度退化性能以及极限位移状态下累积耗能能力进行了评估，综合考察了剪跨比、轴压比、纵筋率、配箍率等因素对桥墩延性性能的影响。可为桥梁的延性抗震设计提供参考。

钢筋混凝土桥墩;拟静力正交试验;延性性能;抗震设计

在文献［1］中，笔者完成了圆形钢筋混凝土桥墩抗震性能拟静力正交试验研究工作，对低周反复荷载作用下桥墩试件的破坏过程、破坏形态、力—位移滞回曲线特性等进行了简要分析。为进一步认识桥墩的延性抗震性能，笔者针对试验数据，对桥墩的变形特征、强度特性、位移延性、等效刚度和刚度退化性能以及极限位移状态下累积耗能能力进行系统的研究，考察剪跨比、轴压比、纵筋率、配箍率等因素对满足 JTG/T B02-01—2008《公路桥梁抗震设计细则》［2］要求的钢筋混凝土桥墩抗震性能的影响。

1 桥墩变形特征［3-4］

1.1 截面平均曲率

截面平均曲率由曲率测试截面层间的5对竖向位移传感器（文献［1］中图1）的位移记录确定。将桥墩东、西两侧相同层间位移传感器记录的相对位移差dm除以对应的传感器测点水平距离Dm，得到相应的层间转角θ，再除以层间高度Hi，即可得到Hi高度范围内的截面平均曲率Φave:

1.2 弯曲变形分量

墩顶位移弯曲变形分量通过层间的弯曲变形和转角对位移的贡献沿墩高累积予以确定。任意层间的弯曲变形为层间转角θ与层间高度Hi乘积的0.5倍;在计算当前层间转角对墩顶位移的贡献时，假定该层间以上部分的弯曲变形是线性分布的，故其对墩顶位移的贡献值为当前层间转角的正弦值与当前层间以上部分墩高的乘积。

1.3 滑移变形分量

滑移变形分量通过墩身最底层10 cm高度处竖向位移传感器（文献［1］中图1）的位移记录计算。虽然该处的位移记录包含了墩底10 cm范围内的弯曲转动效应，但可认为位移变形主要是由纵筋对基座的应变渗透效应引起的。假定墩身绕墩底10 cm区段的中心转动，则滑移变形分量为墩底滑动转角θslip的正弦值与转动中心到墩顶距离的乘积。

1.4 剪切变形分量

剪切变形分量通过层间对角位移传感器确定。对角位移传感器记录的位移包含了截面弯曲转动变形和剪切变形。将由弯曲变形从总位移中扣除，即可得到相应的剪切变形值。然后将剪切变形与初始对角线长度值相加得到只考虑剪切变形后的对角线总长度。给定总对角线的变形长度以及层间初始高度和宽度之后，即可确定由于剪切引起的层间墩身水平位移Δshear（i），各层间剪切变形累积便可得到总的剪切变形分量Δshear。其中，假定墩身截面变形符合平截面假定;同时，假定竖向位移传感器仍然保持为竖向，与传感器安装层之间没有横向偏移，而最高层间以上部分的剪切变形贡献是极小的，可忽略不计。

图1和图2分别给出了部分桥墩的墩身曲率分布和墩顶位移分量变形。由图可知，墩身曲率分布并不总是对称的，在桥墩加载后期，墩底区域转角变形可能会重分布，在墩底10～30 cm左右区段形成所谓的“塑性铰”转动中心，且在同一位移水平的不同循环下，墩底区域的转角、曲率变形也会发生重分布;弯曲变形、滑移变形及剪切变形的总和与墩顶位移吻合良好，说明剥离式三分量墩顶位移测试方法是可靠的，基本上能反映塑性铰区域的变形特征。

图1 墩身曲率分布Fig.1 Curvature distribution of columns

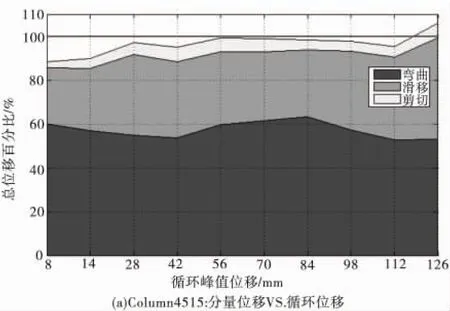
图2 墩顶位移分量变形Fig.2 Component deformations of displacement for column top

2 桥墩强度特性

许多抗震设计标准都指定了评估钢筋混凝土墩柱弯曲强度的方法，了解桥墩在地震荷载作用下的强度特性，对于把握桥梁结构的整体抗震性能是必要的。

为了比较桥墩的理论抗弯能力和实际抗弯强度，在进行桥墩拟静力试验前，先用XTRACT截面分析软件对各桥墩进行截面弯矩-曲率分析，以获取桥墩的理论抗弯能力。截面分析时，以桥墩的设计尺寸、纵筋率、箍筋率、配筋位置以及材料特性的试验值建立纤维截面模型。其中，约束混凝土和非约束混凝土模型采用Mander模型［5］，纵筋采用 XTRACT中的应变强化钢筋模型。表1给出了桥墩截面分析的极限弯矩Mu-XTRACT与试验的极限弯矩Mu-m（取为正、负向最大弯矩的平均值）的比较。Mu-XTRACT/Mu-m的均值及标准差分别为0.92和0.03，表明截面分析所得的极限弯矩是可信的，也从侧面反映所制定的试验方案合理，试验数据可靠。此外，亦可将比较桥墩极限弯矩的理论值与试验值作为检验以往拟静力试验数据可靠性的一种有效手段。

表1 极限弯矩试验值与XTRACT理论值比较Table 1 Comparison of experimental ultimate moment and theoretical value got by XTRACT

3 桥墩位移延性

位移延性是衡量桥墩抗震性能优劣的重要指标。桥墩屈服位移根据Park［6］方法估计（图3所示C点即为屈服点），极限位移状态对应于其力-位移骨架曲线上侧向承载能力降低到最大值的85%［7］（如侧向承载能力未降低到最大值的85%以下，则以纵筋首次断裂为极限位移状态［8］）。桥墩的试验屈服位移、极限位移及对应的位移延性系数如表2。可见，试验桥墩在各轴压水平下都表现了良好的延性性能（Column7024由于墩底区域混凝土未振捣密实，试验过程中过早破坏，位移延性相对较差），表明文献［2］的相关要求及规定是合理的;正交分析的结果表明，轴压比、纵筋率对位移延性系数的影响较大，且位移延性系数有随轴压比、纵筋率的增大而减小的趋势。同时，表2还给出了理论屈服位移 Δcy和试验屈服位移Δy的比较，Δcy/Δy的均值和标准差分别为1.01和0.25，从理论计算和试验结果两方面来看，所制定的位移加载历程是合理的，试验屈服位移的估计方法是可信的。

图3还给出了3个系列桥墩的正规化力-位移骨架曲线。可见，同一系列桥墩试件的骨架曲线形状相似，当桥墩发生明显屈服时，侧向承载力变化较为平缓，直至纵筋屈曲或断裂后，承载力才开始迅速下降，反映了桥墩的延性发展过程。

图3 屈服位移、等效刚度定义及正规化力－位移骨架曲线Fig.3 Definition of yield displacement and effective stiffness，andnormalized lateral load-displacement backbone curves

表2 桥墩位移延性系数Table 2 Displacement ductility coefficients of test bridge columns

4 桥墩等效刚度及刚度退化特性

4.1 等效刚度

为了体现弯曲效应、剪切效应和应变渗透效应对桥墩等效刚度的综合影响，桥墩整体等效刚度定义为其力-位移骨架曲线上屈服点C对应的割线刚度（取为正、负向的平均值，如图3），通过式（5）计算:

表3给出了桥墩整体等效刚度EIeff与其毛截面刚度EcIg的比值，9个桥墩的EIeff/EIg均值为0.3。应该注意的是，由于式（5）中的Δy包含了弯曲变形、剪切变形和黏结-滑移变形，故而式（5）计算的桥墩等效刚度要略小于其弯曲刚度。正交分析结果表明:桥墩整体等效刚度受剪跨比和轴压比的影响较大，而受纵筋率、箍筋率的影响较弱，且随剪跨比、轴压比的增大而增大，这与大多数现有等效刚度计算公式以剪跨比、轴压比作为主要因子是一致的。

表3 桥墩等效刚度Table 3 Effective stiffness of test bridge columns

4.2 刚度退化特性

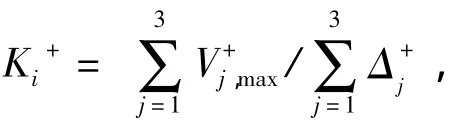
式中:Ki为试件在第i级循环加载时的平均割线刚度，Ki=（+）/2［、分别为3次循环加载的正、负向平均刚度，即（分别为第i级加载正、负峰值位移、分别为正负峰值位移对应的正负侧向荷载）］;Ky为试件等效屈服点的弹性刚度，通过图3中屈服点C的屈服荷载Vy和屈服位移Δy计算。

图4给出了各桥墩βi随位移延性系数的变化趋势。可以看出:3个系列桥墩试件的刚度退化特性相近，在经历等效屈服点后，试件刚度随循环位移的增加迅速下降，但达到极限荷载后，刚度的衰减趋于平缓。

图4 桥墩试件刚度退化特性Fig.4 Stiffness degradation characteristics of bridge column specimens

5 滞回耗能特性

桥墩滞回耗能特性反映了桥墩耗散外来能量以抵抗地震力的能力，这对于桥梁延性抗震较为重要。桥墩的滞回耗能定义为力-位移滞回曲线中封闭滞回环包围的面积，滞回环面积越大，桥墩的耗能能力越强。试验桥墩滞回耗能有如下特点:在相同的位移水平下，由于损伤的累积，后一循环耗散的能量较前一循环耗散的能量小，特别是加载后期，这一特点愈为明显;当纵筋发生屈曲时，桥墩耗散的能量有明显的降低，特别是纵筋断裂时，耗散的能量骤降，如图5。

表4给出了各桥墩极限位移状态下的累计耗散能量，图6则给出了累计耗散能量的正规化图示。从表4和图6中均可看出，极限位移状态下的累计耗散能量与纵筋率直接关联（Column7024除外，由于墩底区域振捣不密实导致提前破坏），而轴压比、配箍率等对其影响不明显。

表4 桥墩极限位移状态下的累计耗散能量Table 4 Accumulative dissipated energy to ultimate displacement of bridge columns

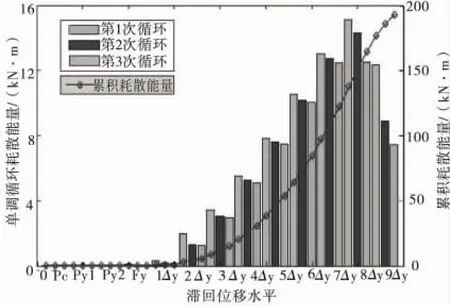
图5 Column 4515滞回耗能特性Fig.5 Dissipated cycle energy of Column 4515

图6 正规化累计耗散能量Fig.6 Normalized accumulative dissipated energy

6 结论

通过拟静力正交试验考察了剪跨比、纵筋率、轴压比、配箍率等对满足文献［2］基本要求的钢筋混凝土桥墩抗震性能的影响。结果表明:

1）剥离式弯曲变形、滑移变形及剪切变形三分量墩顶位移测试方法是可靠的，能基本反映塑性铰区域的变形特征。

2）理论计算的极限弯矩与试验的极限抗弯能力较为吻合。

3）文献［2］对桥墩延性设计的相关要求是合理的，桥墩位移延性受轴压比、纵筋率的影响较大，且随轴压比、纵筋率的增大而减小。

4）桥墩整体等效刚度受剪跨比和轴压比的影响较大，而受纵筋率、箍筋率的影响较弱，且随剪跨比、轴压比的增大而增大。

5）桥墩极限位移状态下的累计耗散能量主要与纵筋率有关，轴压比、配箍率等对其影响不明显。

6）Column7024由于墩底区域混凝土振捣不密实，导致位移延性及耗能能力相对较差，对桥墩的延性抗震能力有较为不利的影响。

（References）:

［1］ 李贵乾，郑罡，王军.圆形钢筋混凝土桥墩抗震性能试验评估（Ⅰ）:试验设计及初步结果［J］.重庆交通大学学报:自然科学版，2011，30（5）:889-894，1000.

LI Gui-qian，ZHENG Gang，WANG Jun.Experimental evaluation of the seismic performance of circular reinforced concrete bridge columns（Ⅰ）:Design and result of the experiment［J］.Journal of Chongqing Jiaotong University:Natural Science，2011，30（5）:889-894，1000.

［2］ JTG/T B 02-01—2008公路桥梁抗震设计细则［S］.北京:人民交通出版社，2008.

［3］ Lehman D E，Moehle J P.Seismic performance of well-confined concrete bridge columns［R］.California:PEER and University of California，Berkeley，1998.

［4］ Calderone A J，Lehman D E，Moehle J P.Behavior of reinforced concrete bridge columns having varying aspect ratios and varying lengths of confinement［R］.California:PEER and University of California，Berkeley，2001.

［5］ Mander J B，Priestley M J N，Park R.Theoretical stress-strain model for confined concrete［J］.Journal of the Structural Division ASCE，1988，114（8）:1804-1826.

［6］ Park R.Evaluation of ductility of structures and structural assemblages from laboratory testing［J］.Bulletin of the New Zealand National Society for Earthquake Engineering，1989，22（3）:155-166.

［7］ 范立础，卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001.

［8］ 李贵乾.钢筋混凝土桥墩抗震性能试验研究及数值分析［D］.重庆:重庆交通大学，2010.

［9］ 司炳君，李宏男，王东升，等.基于位移设计的钢筋混凝土桥墩抗震性能试验研究（I）:拟静力试验［J］.地震工程与工程振动，2008，28（1）:123-129.

SI Bing-jun，LI Hong-nan，WANG Dong-shen，et al.Experimental evaluation of the seismic performance of reinforced concrete bridge piers designed on the basis of displacement（I）:Quasi-static test［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（1）:123-129.

Seismic Performance of Circular Reinforced Concrete Bridge Columns（Ⅱ）:Evaluation of Experimental Results

LI Gui-qian1，2，ZHENG Gang2，WANG Jun3
（1.Communications Planning，Survey ＆ Designing Institute of Guangxi Zhuang Autonomous Region，Nanning 530011，Guangxi，China;2.State Key Laboratory of Bridge Structural Dynamics，Chongqing Communications Research ＆ Design Institute，Chongqing 400067，China;3.School of Civil Engineering＆ Architecture，Chongqing Jiaotong University，Chongqing 400074，China）

According to the failure phenomenon and test data in the orthogonal quasi-static test，the characteristics of deformation and flexural strength of circular reinforced concrete bridge columns are studied.And the displacement ductility，effective stiffness，stiffness degradation and capacity of accumulative energy dissipation to ultimate displacement state of bridge columns subjected to low-cyclic loading have been evaluated，so as to investigate the influence of factors such as shear-span ratio，axial-load ratio，and longitudinal reinforcement ratio and spiral reinforcement ratio on ductility performance of bridge columns.Finally，some useful conclusions are found out for the ductile anti-seismic design of highway bridges.

reinforced concrete bridge columns;pseudo-static orthogonal test;ductility capacity;seismic design

U445.7+5

A

1674-0696（2011）06-1270-05

10.3969/j.issn.1674-0696.2011.06.02

2011-05-31;

2011-06-13

交通运输部西部交通建设科技项目（2007 318 822 33）;重庆市杰出青年科技基金资助项目（CSTC，2008BA6039）

李贵乾（1984-），男，广西桂林人，硕士，主要从事桥梁抗震设计研究。E-mail:lgqmancan@163.com。