铁路客运列车悬架参数稳健性设计*
2011-06-02廖耘,杨岳,王婷
廖 耘,杨 岳,王 婷
(中南大学交通运输工程学院,湖南长沙 410075)
铁路客运列车悬架参数稳健性设计*
廖 耘,杨 岳,王 婷
(中南大学交通运输工程学院,湖南长沙 410075)
铁路车辆的悬架参数对车辆运行平稳性和舒适性具有重要的影响。为了保证车辆在动态变化的运行工况下具有良好的稳定性,对车辆悬架参数稳健性进行设计。综合考虑车辆一系悬挂和二系悬挂的车辆六自由度垂向动力学模型与悬架参数对运行平稳性的影响。采用田口方法稳健性设计原理,研究确定了车辆悬架参数稳健性设计流程及悬架设计参数中的可控因素和外界噪声因素。在此基础上,进行悬架参数内外正交表设计,并利用Matlab编程分析计算了在多种典型工况下的运行平稳性指标值。分析结果表明:通过对多种工况下车辆Sperling指标和信噪比的分析比较,得到了稳健性最优的悬架参数组合,较好地解决了变工况下车辆悬架刚度和阻尼的匹配问题。
稳健性设计;运行平稳性;悬挂参数
稳健性(robustness)指因素状况发生微小变差对因变量影响的不敏感性[5-6]。稳健设计就是通过调整设计变量及控制其容差使可控因素和不可控因素当与设计值发生变差时仍能保证产品质量的一种工程方法[7-8]。车辆悬架参数稳健性设计的目的在于寻找一组最佳的悬架设计参数,使车辆在运行工况变化情况下,仍能达到较优的运行平稳性。
本文利用车辆垂向动力学模型描述车辆悬架弹簧、减振器的性能参数对运行平稳性的影响,以田口方法作为悬架参数稳健性设计的基本工具,对铁路客车运行平稳性的悬架参数稳健性设计,以使得铁道车辆在不同的运行工况条件下,均能满足具有良好的运行平稳性要求。
1 车辆运行平稳性分析模型
为使车辆自振频率降低,铁路客车一般采用两系悬挂装置提高运行平稳性。车辆在运行过程中的振动是一个很复杂的问题,为了使车辆模型精确化,采用四轴串联的两系弹簧悬挂车辆模型来描述车辆的垂向振动[9],如图1所示,图中参数值如表1所示。

图1 铁路客车垂向振动模型Fig.1 Railway passenger vertical vibration model
图1中各参数的意义:Mc和Mb分别为车体及一个构架的质量;Ic为车体绕通过其重心的y轴的转动惯量;K1和K2分别为转向架一系垂向刚度和二系垂向刚度;C1和C2分别为转向架一系垂向阻尼和二系垂向阻尼;L,Lb和Lw分别为车体总长、转向架定距之半和轴距之半;Zc,Zb1和Zb2分别为车体及一、二位构架的沉浮振动位移;θ1,θ2和θ3分别为车体及一、二位构架的点头振动角位移。

表1 铁路客车垂向模型参数Table 1 Railway passenger vertical model parameters
2 车辆悬架参数稳健性设计
2.1 基于田口方法的车辆悬架参数稳健性设计原理
基于“田口方法”的稳健性设计是一种低成本、高效益的质量工程方法,由日本田口玄一博士提出。田口方法强调设计对质量的重要作用,将质量重点由制造阶段前移到设计阶段。田口稳健参数设计是基于损失模型的稳健设计,主要通过对信噪比(S/N)的正交试验等进行分析。田口稳健性参数设计有2个基本工具:一是正交实验设计;二是由平均损失函数演变而来的信噪比。通过信噪比可将损失模型转换为信噪比指标并作为衡量产品质量的特性值,信噪比越大稳健性越好。正交试验设计方法只需要完成少数试验就能较全面反映出试验条件完全组合的内在规律,以确定参数的最佳组合,以提高设计效率。
根据田口方法稳健性设计原理,车辆悬架参数的稳健性设计过程如图2所示。具体如下:在建立车辆运行平稳性垂向动力学模型基础上,选定悬架可控因子和噪声因子,设计内外正交试验表。然后,利用Matlab编程计算正交表内各工况下的运行平稳性Sperling指标值,得到各组合情况下的对应数据。在此基础上,采用质量管理软件Minitab中的田口试验设计工具,处理内外正交表试验数据,得到在噪声因素变动情况下的悬架可控因子各组合的Sperling均值和望小特性信噪比,经分析比较得到悬架稳健性设计最佳参数组合。
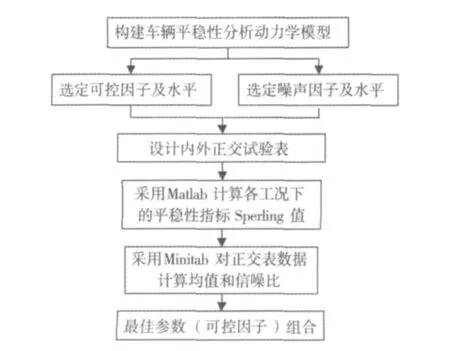
图2 车辆悬架参数稳健性设计流程Fig.2 Vehicle suspension parameters robustness design process
2.2 车辆悬架的可控因子和噪声因子
为进行车辆悬架参数稳健性设计,需确定悬架参数的可控因子与噪声因子。由于悬架一系和二系刚度和阻尼对运行平稳性和乘坐乘坐舒适性具有较大影响,且属于可调整的设计参数,故主要选择一系二系刚度和阻尼为可控因子。又由于车辆载荷和车速对运行平稳性也具有较大影响,且属于不能调整的设计条件,故将车速和载荷(载客量)设为噪声因子。
四是以宣传培训为抓手营造良好社会氛围。组织部门应把人大制度理论纳入领导干部特别是镇街党(工)委书记教育培训的重要内容,通过邀请人大专家授课、开展民主法治教育等形式,提高镇街党(工)委书记对人大工作重要性的认识,提高强化其把党委决策与人大依法行使职权相结合的意识;宣传部门和新闻单位应把宣传人大工作列入年度工作计划,开展常态化、有针对性的宣传,及时报道人大工作中涌现出的好典型、好经验,提高全社会对人大工作的认知度。人大常委会应重点抓好镇街人大干部和代表的学习培训,通过举办学习班、交流研讨会等,使其深刻理解人大工作的性质和特点,熟悉掌握履职的程序和方法。
为了详细分析车辆悬架可控因子和噪声因子对车辆运行稳定性的的影响,根据车辆实际运行工况,每个因子的水平选择如表2所示。

表2 车辆悬架因子水平表Table 2 Vehicle suspension parameters level table
2.3 内外正交试验表设计
根据田口方法用一个正交表对可控因子和水平进行安排,称为内表(Inter Array)设计,采用另外一个正交表对噪声因子和水平进行安排,称为外表(Outer Array)设计,一般情况下内表为横,外表为纵,纵横交错,这样做就相当于可控制表中的每个水平组合与噪声表中的每个组合相乘构成一个乘积表(Cross Array),这样就形成了一个田口式的试验设计。
根据田口方法设计内外正交试验表,一系悬挂的垂向刚度和阻尼(K1,C1)、二系悬挂的垂向刚度和阻尼(K2,C2)四个因素放置在内表,选择L25(54)标准正交表;载客量(M)和车速放置(V)在外表,选择L12(3'×6')标准正交表,如图3所示。
2.4 信噪比的确定
Sperling指标在国际上广泛用来评价车辆运行平稳性。Sperling平稳性指标计算公式为:

式中:j为振动加速度,cm/s2;f为振动频率,Hz;F(f)为频率修正系数。
对于垂向振动,F(f)计算公式为:

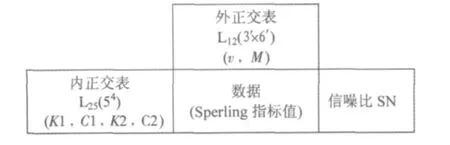
图3 田口试验表Fig.3 Taguchi test table
实际上车辆是随机振动的,振动的加速度和频率都随时间而变化,此时需要将振动波形按频率分组。实际评定时将所要分析的加速度波形按频率分组,根据每一组的加速度和频率计算该组的平稳性指标Wi,对每组进行合成,总的平稳性指标表达式为:

式中,N为整个波段的分组总数。表3为我国客车车辆运行平稳性评定等级。

表3 我国客车车辆平稳性评定等级Table 3 China's passenger vehicle ride quality rating
根据车辆运行平稳性指标可知,平稳性指标越小车辆运行越稳定,即函数的均值μ和方差σ2越小越好,考虑到信噪比越大越好,设信噪比RSN为:

对式(4)取常对数转化为分贝值,得:
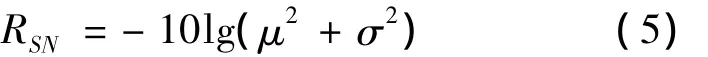
式中,μ2+σ2根据概率统计知识可用输出函数值的无偏估计代替,转化后的信噪比为:

式中,yi为相应目标函数输出值,即Sperling平稳性指标值。
3 悬架参数稳健性分析
根据2.3节所述正交试验表设计原理,得到如表4所示的悬架参数内外正交试验表的内表和外表。利用Matlab对车辆运行平稳性垂向动力学模型进行编程计算,得到正交试验表中各组合工况下的Sperling指标值。采用Minitab软件中的田口试验设计处理工具,在噪声因子变动情况下,得到表4中可控因子各组合情况下的Sperling均值和望小特性信噪比SNR值。

表4 基于内外正交表的Sperling指标值和信噪比Table 4 Sperling indexes and SNR of internal and external orthogonal table
从表4可以看出,试验10(K1=1 100 KN/m,C1=35 kN·s/m,K2=150 kN/m,C2=15 kN·s/m)的信噪比值在车辆各种不同的行驶工况下最大,根据信噪比越大越稳健的特性,该试验的悬架参数稳健性最好。
根据表4的内外正交表,得在望小特性下可控因子(K1,C1,K2和C2)在各水平下的信噪比,以及噪声因子(V和M)在各水平下的信噪比,结果如表5所示。

表5 望小特性各因子信噪比反应表Table 5 Each factor SNR reaction table of smaller-thebetter characteristic
根据表5所示因子反应可绘制出各因子的水平趋势图,图4是K1因子在各水平下的信噪比主效应图,图5是K2因子在各水平下的信噪比主效应图,图6是C1因子在各水平下的信噪比主效图应图,图7是C2因子在各水平下的信噪比主效图应图,图8是V因子在各水平下的信噪比主效应图,图9是M因子在各水平下的信噪比主效应图。

图4 K1因子各水平的信噪比主效应图Fig.4 K1 factor main effects of each level SNR

图5 K2因子各水平的信噪比主效应图Fig.5 K2 factor main effects of each level SNR
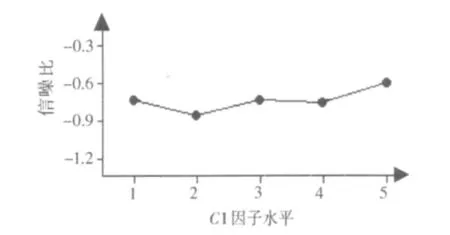
图6 C1因子个水平的信噪比主效应图Fig.6 C1 factor main effects of each level SNR
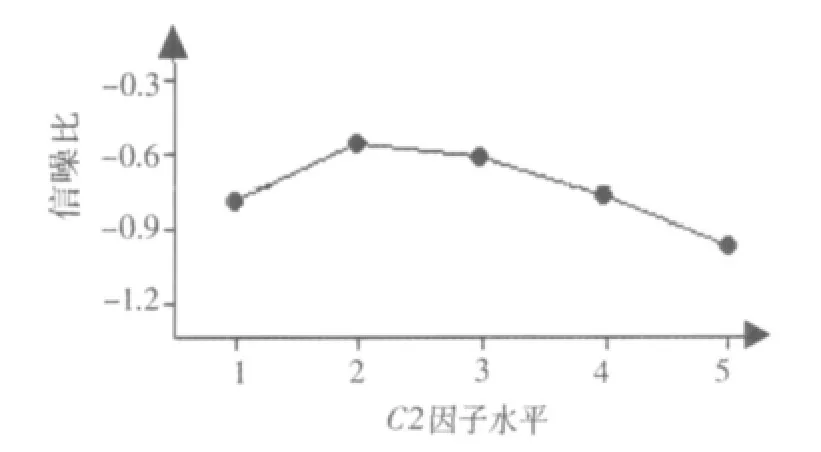
图7 C2因子各水平的信噪比主效应图Fig.7 C2 factor main effects of each level SNR

图8 V因子各水平的信噪比主效应图Fig.8 V factor main effects of each level SNR

图9 M因子各水平的信噪比主效应图Fig.9 M factor main effects of each level SNR
根据图4~图7的可控因子水平趋势可知,最优组合K1,C1,K2和C2的水平取1,5,1和2 。根据图8~图9可知,噪声因子的影响趋势是:随着车辆速度的增加,信噪比值呈下降趋势,随载荷的增加,信噪比值呈上升趋势。
稳健性设计前后的可控因子(K1,C1,K2和C2)在噪声因子(V和M)变化的影响情况下的Sperling平均值和信噪比如表6所示。
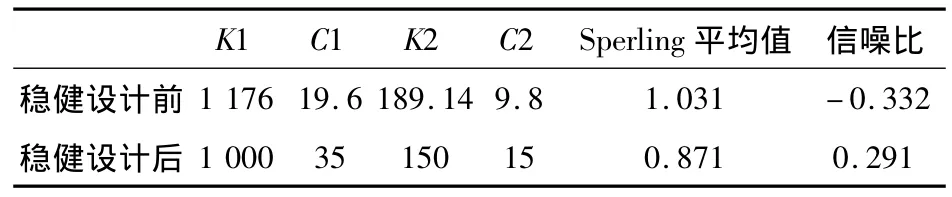
表6 稳健设计前后车辆Sperling平均值和信噪比Table 6 Vehicle Sperling averages and SNR of robust design before and after
从表6可以看出,稳健性设计后车辆运行平稳性值从1.031下降到0.871,根据表3可知车辆运行平稳性较好,但效果不是很明显。稳健性设计后信噪比(SNR)的值从初始值 -0.332上升到0.291,在车辆运行平稳的情况下稳健性得到较大的提高。因此通过稳健性设计,车辆在运行工况变化的情况下,车辆的运行平稳性良好,稳健性得到了显著提高。
4 结论
(1)通过引入车辆六自由度垂向动力学模型,为车辆悬架参数对平稳性的影响提供了理论分析依据。
(2)设计了基于田口方法的车辆悬架参数稳健性设计流程,并以一系和二系悬架垂向刚度和阻尼作为可控因子,车辆运行速度和载客量和噪声因子,确立了悬架参数稳健性设计基本方案。
(3)利用Taguchi方法设计内外正交表,根据正交表中车辆平稳性指标值计算出多种典型工况下的信噪比,根据信噪比越大越稳健的特点得到了稳健性最优的悬架参数组合,解决了变运行工况下车辆悬架刚度和阻尼不匹配问题,从而使车辆运行平稳性得到提高。所得结果对铁道车辆悬架参数设计和优选具有指导意义。
[1]郝建华,曾 京,邬平波.铁道客车垂向随机减振及悬挂参数优化[J].铁道学报,2006,28(6):36 -39.
HAO Jian-hua,ZENG Jing,WU Ping-bo.Optimization of vertical random vibration isolation and suspension parameters of railway passenger car systems[J].Journal of the China Railway Society,2006,28(6):36 -39 .
[2]郑仲浪,吕彭民.基于舒适性及道路友好性的拖挂车辆悬架参数优化方法[J].交通运输工程学报,2009,9(5):50-53.
ZHANG Zhong-lang,LU Peng-min.Optimization method of suspension parameters for articulated vehicle based on ride comfort and road-friendliness[J].Journal of Traffic and Transportation Engineering,2009,9(5):50-53.
[3]Sayyaadi H,Shokouhi N.New dynamics model for rail vehicles and optimizing air suspension parameters using GA[J].Mechanical Engineering,2009,16(6):496 -512.
[4]车华军,陈 南,殷国栋.基于操纵稳定性的车辆悬架性能参数稳健设计方法[J].汽车工程,2009,31(4):371-375.
CHE Hua-jun,CHEN Nan,YIN Guo-dong.Robust design of suspension performance parameters for vehicle handling and stability[J].Journal of Automotive Engineering,2009,31(4):371 -375.
[5]黄 滢.基于MATLAB的稳健性优化设计方法研究[D].北京:北京林业大学,2006.
HUANG Ying.Robust and optimization design with Matlab[D].Beijing:Beijing Forestry University,2006.
[6]Au F T K,Cheng Y S,Tham L G,et al.Robust design of structures using convex models[J].Computers and Structures ,2003:81,2611 -2619.
[7]陈立周.工程稳健性设计的发展现状与趋势[J].中国机械工程,1998,9(6):59 -62.
CHEN Li- zhou.Engineering design robustness the current situation of the development and trend[J].China Mechanical Engineering,1998,9(6):59 -62.
[8]Zang C,Friswell M I,Mottershead J E.A review of robust optimal design and its application in dynamics[J].Computers and Structures ,2005,83:315 -326.
[9]彭 波.铁道客车乘坐舒适性建模、仿真与虚拟试验研究[D].长沙:中南大学,2010.
PENG Bo.Research on modeling,simulation and virtual test of riding comfort of passenger railway vehicle[D].Changsha:Central South University,2010.
Robust design of suspension parameters for railway passenger train
LIAO Yun,YANG Yue,WANG Ting
(School of Traffic and Transportation Engineering,Central South University,Changsha 410075,China)
Suspension parameters of railway vehicles have an important influence on ride quality and ride comfort of vehicles.In order to guarantee a good ride quality under dynamic changes of running condition,robustness is designed to vehicle suspension parameters.A 6 freedom degree vertical dynamics model is introduced with comprehensive consideration of primary and secondary suspension,and suspension parameters on the effect of ride quality is described in the vertical dynamics model.Through Taguchi robust design theory,the robust design process of vehicle suspension parameters and the controllable factors and external noise factors of suspension design parameters are studied and determined.On this basis,internal and external orthogonal tables are designed about suspension parameters,and the evaluation indicators of vehicle ride quality are calculated under all kinds of typical working conditions by Matlab programming.Analysis results show that optimization and robust design of vehicle suspension parameters are achieved by comparing Sperling index with signal to noise ratio,and a good solution for reasonable matching between vehicle suspension stiffness and damping is provided under changing running conditions.
robust design;ride quality;suspension parameters
U270.2
A
1672-7029(2011)05-0090-06
2011-06-30
廖 耘(1963-),男,湖南益阳人,研究员,从事轨道交通设备设计、运用与维护研究
