用Matlab实践中成药配置的数据分析*
2011-06-02李晓伟王益民肖二钢张皓楠
李晓伟,王益民,肖二钢,张皓楠
矩阵实验室(Matlab)是一套高性能的数值计算和可视化软件,其中大量的工具箱可以方便地实现各种数据的分析算法,便于医学工作者掌握。下面针对Matlab数据分析功能在中成药配置中的应用作介绍。
1 Matlab中向量与矩阵运算
1.1 向量及矩阵的生成 在Matlab中,向量可视作是特殊的矩阵,n维行向量是1行n列的矩阵,n维列向量是n行1列的矩阵。因此,向量的输入方法与矩阵相同,但行向量要转置为列向量参加运算。
在Matlab中输入矩阵需要遵循以下基本规则:1)整个输入矩阵必须包含在方括号“[]”中。2)在矩阵中,采用分号或回车表明每一行的结束。3)矩阵每一行的元素必须用空格或逗号分开[1]。
1.2 向量和矩阵的运算

1.3 向量组的线性相关性 向量之间,除了运算关系外,还有向量组的线性相关和线性无关。
1.3.1 线性组合 对于向量 a,a1,a2,…,am,如果有一组数 k1,k2,…,km,使得

则称向量a是a1,a2,…,am的线性组合。
1.3.2 线性相关 设a1,a2,…,am为n维向量组,则这m个向量线性相关的充分必要条件是其中至少一个向量可以用其余向量线性表示。
1.3.3 极大线性无关组 设有一组n维向量,如果这一组向量中存在一组向量 a1,a2,…,ar满足:1)a1,a2,…,ar线性无关。2)在原来的那一组向量中任取一个向量 a 加进去,则 a1,a2,…,ar,a 线性相关;那么称a1,a2,…,ar是这一组向量的一个极大线性无关组,极大线性无关组所含的向量个数r称为向量组的秩。
1.4 Matlab的数组与矩阵
1.4.1 数组与矩阵的概念 Matlab是“Matrix Laboratory”之意,即矩阵实验室。Matlab最初是为了解答线性代数的问题而开发的,以矩阵作为基本的运算单元。
数组(Array)是由一组复数排成的长方形阵列。数组是进行数值计算的基本处理单元,一行多列的数组是行向量;一列多行的数组是列向量;数组可以是二维的,也可是三维,甚至是多维的。在Matlab中,大量数值计算是以数组形式进行的,数组的所有运算都是对被运算数组中的每个元素平等执行同样的操作,矩阵运算是把矩阵整体当做一个量进行运算的。
1.4.2 数组或矩阵元素的标识、访问与赋值 1)一维数组(行向量)是使用方括号以及在括号内列出以空格或逗号分隔其元素的表。元素是用数组名后方括号内的元素在数组中位置的顺序号来标识的,数组元素的访问与赋值就是根据数组元素的标识进行的。例如在Matlab命令窗口中输入:>>X=[1*pi 2*pi 3*pi 4*pi 5*pi],回车得到:X=3.14 6.28 9.42 12.56 15.70。2)多维数组或矩阵元素的标识,即多维数组元素定位地址。其元素标识通用双下标。例如:A(m,n)[2]。
2 Matlab与中成药生产的结合
中国的中药产业飞速发展,但在现阶段的中成药生产中对各组分相关度研究甚少。应用Matlab自身携带的数据分析功能,通过对实际中成药配置中的数据进行相关性分析,在已知矩阵基础上找到其中具有关联性的数组,对比实际生产确定参数,对中成药制药业的发展具有实际意义。
利用Matlab软件中的数据分析工具分析实际生产过程中的大量数据,从相关性、变异性等多个方面通过具体数据和图形方式显示分析结果,从而起到指导中药生产的作用。可以用Matlab对中成药复方配伍中的关联数据进行相关性分析,相关性分析是用来揭示事物之间的关联性,中成药是由多个单味药组成并受多种因素影响的过程,所以在配置新药的时候应多方考虑,这时就可借助相关性分析来得到客观合理的结果。
用相关性分析作定量的研究方法:1)Pearson积差相关系数,是计算两个变量线性相关的系数,用r或rxy示,其作用是考察的两个变量x与y组成的二维随机向量(X,Y)的样本相关系数。X与Y存在线性相关程度越小,r=0,可以认为X与Y不相关(不存在线性相关),但不等于X与Y相立,X与Y之间可能存在其他形式的相关关系。在-r-≠0时,若r>0,可认为X与Y正相关;若r<0可认为X与Y负相关。2)Kendall(肯德尔)和谐系数,是计算多个等级变量相关程度的一种相关量,适用于数据资料是多列相关的等级资料,既可以是k个评分者评n个对象,也可以是同一个人先后k次评n个对象。通过求得Kendall和谐系数,可以较为客观地选择好的产品。3)Spearman秩相关系数,又称等级相关系数,或顺序相关系数,是将两要素的样本值按数据的大小顺序排列位次,以各要素样本值的位次代替实际数据而求得的一种统计量。
Matlab以数组和矩阵为基础,具有丰富的库函数,是集通用科学计算、绘图及程序设计于一体的高效科学计算软件,在环境中集成了优化计算、数理统计等工具箱,其强大的功能和运用的灵活,适合中成药配置中的数据分析。
3 Matlab与中成药配制结合应用举例
某中药厂用8种中草药(A-H),根据不同的比例配制成了7种中成药,各用量成分见表1。
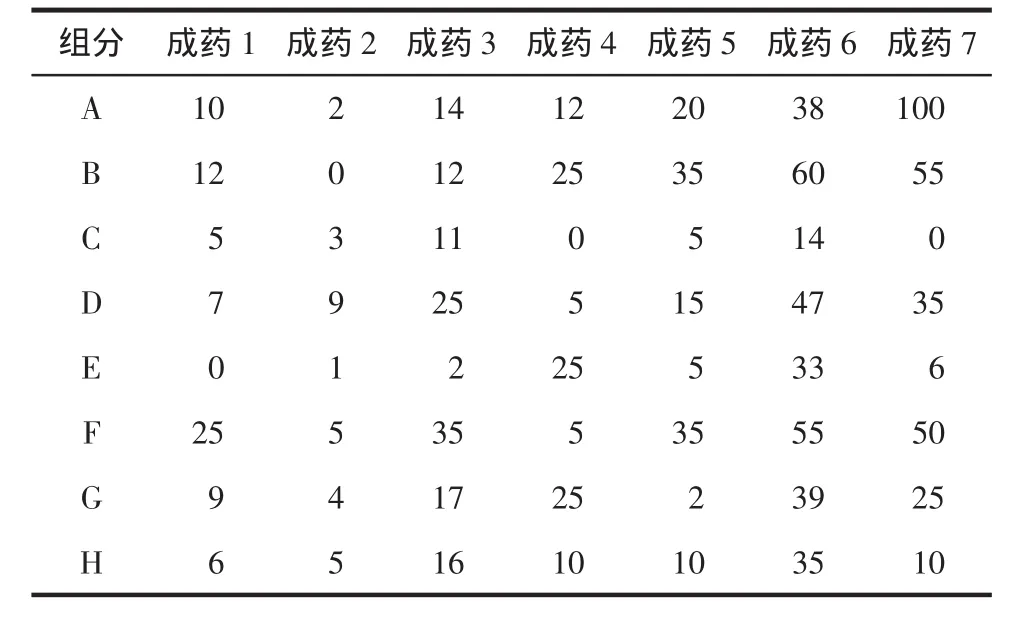
表1 中成药配置成分表g
某医院要购买这7种特效药,但药厂的第3号药和第6号药已经卖完,请问能否用其他特效药配制出这两种脱销的药品?
在Matlab窗口输入

计算结果为

因为初等行变换不改变列向量的线性相关性和线性表示的系数,所以从最简行阶矩阵U0中可以看出,向量组线性相关,一个最大无关组为u1,u2,u4,u5,u7,u3=u1+2u2,u6=3u2+u4+u5故可以配制新药。
现在该医院想用这8种草药配制2种新的特效药,表2给出了2种新的特效药的成分,请问能否配制?如何配制?

表2 特效药配置成分表g
两种新药用v1,v2表示,问题化为v1,v2能否由u1-u7线性表示,若能表示,则可配制;否则,不能配制。
在Matlab窗口输入


计算结果为

从最简行阶矩阵U0可以看出,向量组线性相关,一个最大无关组为 u1,u2,u4,u5,u7,v1=u1+3u2+2u4,v2=3u1+4u2+2u4+u7,故可以配制新药。
4 结语
应用计算机技术进行中药生产的数据分析,是目前计算机应用的重要领域。在中药生产的数据分析领域内,国内做的研究正处于起步阶段,Matlab的数据分析功能是十分强大的,将Matlab应用到中药生产数据分析领域将对生产起到重要的指导作用。
[1]张德丰.Matlab数值计算方法[M].北京:机械工业出版社,2010:1-37.
[2]周仁郁.线性代数[M].北京:中国中医药出版社,2006:58-66.
