基于遗传算法的连通式油气悬架平顺性与道路友好性参数优化

杜 恒，魏建华

(浙江大学 流体传动及控制国家重点实验室，杭州 310027)

连通式油气悬架以其良好的变刚度特性、参数易于调节、较大的储能比、较大的抗侧倾刚度和易于实现车身姿态控制等优点，在大型工程车辆上应用广泛，然而连通式油气悬架在设计时大多未能同时考虑车辆平顺性及道路友好性，而大型工程车辆自重很大且有时行驶路况较差，这不仅会造成车身的剧烈振动，而且车轮动载荷对路面的破坏也较大，所以优化选择连通式油气悬架的各参数使整车同时具有良好的平顺性和道路友好性具有重要意义［1－3］。

连通式油气悬架的机液模型具有多个非线性元件，通过列解数学模型或单一软件仿真很难简单有效的实现参数优化，故在分析连通式油气悬架结构、工作原理及相应数学模型基础上，结合ADAMS、AMESim及Simulink各自优点，建立系统联合仿真模型。同时，分析平顺性与道路友好性评价标准并建立归一化的多目标优化函数，采用遗传优化算法进行迭代计算，最终分析出综合性能最优的连通式油气悬架参数，使平顺性与道路友好性均有所改善，为大型工程车辆油气悬架的综合性能参数优化提供有效参考。

1 结构及工作原理

将大型工程车辆连通式油气悬架整车部分进行简化，可得如图1所示七自由度整车连通式油气悬架模型，模型主要由车身、前后桥、内置阻尼元件与单向阀的悬架缸、蓄能器、管路和轮胎组成，轮胎可简化为线性弹簧阻尼系统。悬架缸为主要承载元件，承受车身的重量，蓄能器为刚度元件，当车辆行驶时，蓄能器通过充放油来缓和由路面造成的冲击，阻尼孔、单向阀及管路共同构成系统的阻尼元件，当车辆行驶时，油液来回的通过阻尼元件衰减振动并吸收能量，各元件共同作用最终达到隔离振动、降低车轮动载荷的目的。

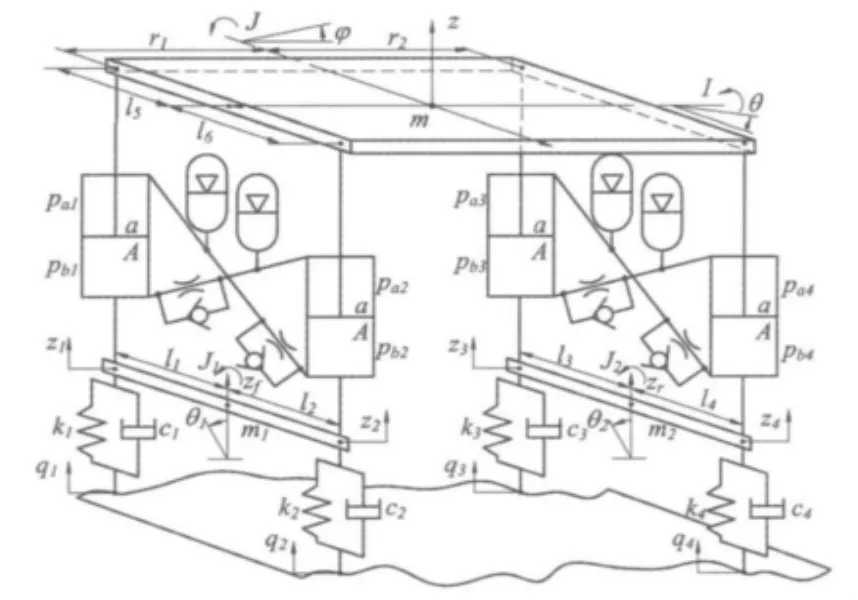
图1 七自由度整车连通式油气悬架模型Fig.1 7－ DOF whole vehicle interconnected hydro-pneumatic suspension model

工程车辆行使时，车身的加速度和车轮动载荷反映平顺性和道路友好性，这些参数与路面不平度、车辆行驶速度特别是车辆悬架系统的参数关系密切，调整悬架系统参数即可调整车辆的平顺性和道路友好性，所以合理优化配置悬架参数即可有效提高车辆的综合性能［4－6］。

2 模型建立

为了寻找最优的平顺性和道路友好性参数，首先需要建立相应模型进行分析，在明确相应数学模型基础上，建立ADAMS/Simulink/AMESim联合仿真模型，并采用相应算法进行优化分析得出优化结果，这样可发挥各自软件优点，使模型更加准确，优化结果也更加可靠。

2.1 整车七自由度质量－弹簧－阻尼系统振动模型

根据图1所示的七自由度整车连通式油气悬架模型，可得出整车系统振动微分方程式［5，7］:

车身具有垂向振动z、侧倾θ、俯仰φ三个自由度，前桥具有垂向振动zf、侧倾θ1两个自由度，后桥同样具有垂向振动zr、侧倾θ2两个自由度，故整车模型共有七个自由度。m为车身质量;I为车身侧倾转动惯量;J为车身俯仰转动惯量;l5、l6为车身质心到左右悬架缸支撑处的距离;r1、r2为车身质心到前后桥的距离;m1、m2为前后桥质量;J1、J2为前后桥侧倾转动惯量;l1、l2为前桥质心到左右悬架缸支撑处的距离;l3、l4为后桥质心到左右悬架缸支撑处的距离;z1～z4为四个车轮处垂向振动;k1～k4为四个车轮的等效刚度;c1～c4为四个车轮的等效阻尼;q1～q4为四个车轮处路面的随机激励;pa1～pa4为四个悬架缸有杆腔压力;pb1～pb4为四个悬架缸无杆腔压力;a，A为悬架缸有杆腔与无杆腔面积。

图2 七自由度整车连通式油气悬架ADAMS模型Fig.2 7-DOF whole vehicle interconnected hydropneumatic suspension model based on ADAMS

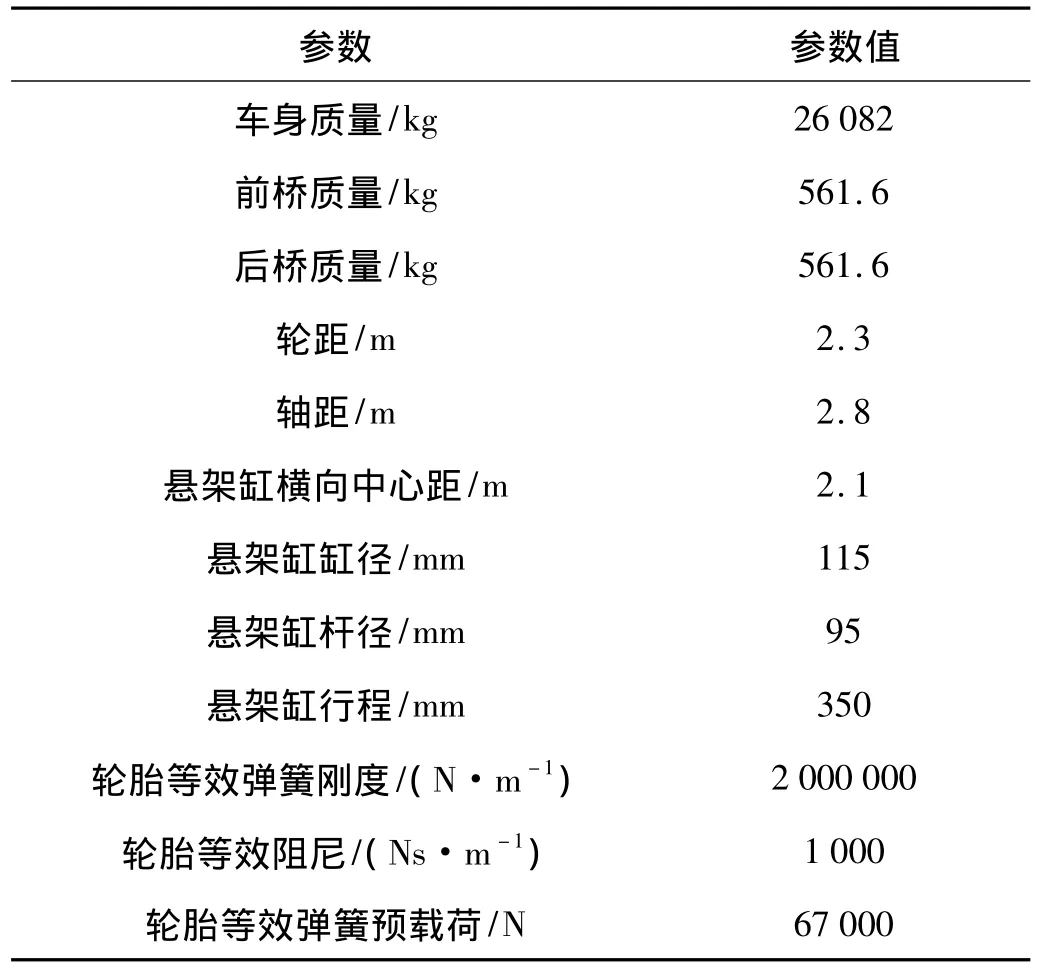
表1 整车系统振动模型主要参数Tab.1 Main parameters of the whole vehicle vibration model

在ADAMS/View中建立与式(1)相应的整车连通式油气悬架振动模型如图2所示，模型中所有零件均设置为刚体，建立各零件间运动副且各运动副内摩擦力、内部间隙忽略不计，采用ADAMS简单约束模块中的点面约束设置相应约束，使车身仅具有垂向振动、侧倾和俯仰三个自由度，使前桥仅具有垂向振动和侧倾两个自由度，使后桥仅具有垂向振动和侧倾两个自由度，模型各主要参数设置如表1。

2.2 路面模型

由于连通式油气悬架模型具有复杂非线性，联合仿真时需要重构一段时间域的路面信号，采用物理意义明确、计算方便的滤波白噪声法进行路面重构，依据路面谱数值和行驶速度确定路面模型参数。对于整车模型而言，必须考虑左右轮路面输入相关性和前后轮输入相关性，则建立四轮相关路面输入状态方程如下［8］:

式中:Sq(n0)为路面不平度系数;n0为标准空间频率，n0=0.1 m－1;W(t)为均值为零的高斯白噪声;v0车辆行驶速度;nc为路面空间下截止频率，nc=0.01 m－1;B为左右两侧轮距;L为前后轴距;x1、x2、x3、x4为中间状态变量。

根据四轮相关路面输入状态方程，在Simulink中建立路面仿真模型，选择常见C级路面进行分析，则路面不平度系数Sq(n0)取256×10－6m3/cycle，左右侧轮距B和前后轴距L与整车振动模型相同分别取2.3 m和2.8 m，车辆行驶速度 v0取 60 km/h，即 v0=16.67 m/s。由于模型中首先要产生均值为零的高斯白噪声，应用Matlab库函数WGN(2000，1，20)产生采样时间为0.01 s持续20 s且功率为20 DBW的高斯白噪声序列，由此序列来产生相应的路面谱时域模型，时域曲线如下图:

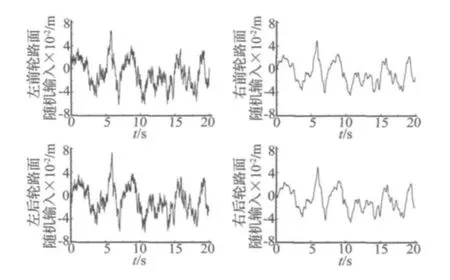
图3 四轮相关的C级路面时域曲线Fig.3 C-grade road roughness curve with four wheels correlated in time domain

2.3 液压系统模型

在油气悬架系统中，液压部分模型主要包括悬架缸、蓄能器、单向阀、液阻、管路，这些数学模型可参考文献［11］，但由于液压系统中液压油的压缩性、元件的非线性特性及泄漏、库仑力等因素对系统均有一定影响，为了使模型能够精确的反映实物，采用专用液压系统建模仿真平台AMEsim，该平台充分考虑液压系统特性并具有强大的解算能力。依据图1建立液压部分AMESim的仿真模型如图4所示，AMEsim模型中悬架缸的各结构尺寸参数同表1，重要液压元件参数设置如表2所示。

表2 重要液压元件参数Tab.2 Parameters of main hydraulic component

3 平顺性与道路友好性综合性能评价

3.1 评价指标及目标优化函数

车辆的平顺性和道路友好性都是评价车辆性能的重要指标，为了同时具有良好的平顺性和道路友好性，首先需对其评价方法进行分析:对于平顺性而言，依据ISO2631－1:1997(E)规定，可采用总加权加速度均方根值对车辆平顺性能进行评价。将加速度时间历程经过变换得到功率谱密度函数，然后再与频率加权函数进行加权积分处理，得到最终的加速度加权均方根值，由于图1所示模型仅分析Z轴方向，故忽略X和Y轴方向加速度值，故总加速度加权均方根值表述如下式:

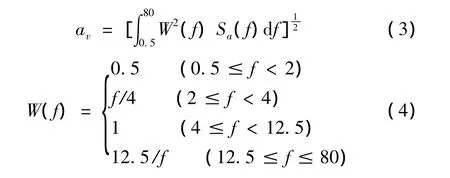
式中:W(f)为频率加权函数，Sa(f)为车身加速度时间历程经过频谱分析后得到的功率谱密度函数。式(3)建立的总加权加速度均方根值与路面条件、车辆结构及车速有关，油气悬架参数对平顺性能的影响关系可由此式进行分析。

汽车对道路破坏潜力的大小可描述为道路友好性，破坏潜力越大，道路友好性就越差。道路友好性评价指标主要包括动载荷系数、动态载荷应力因子及95百分位四次幂和力评价指标。由于95百分位四次幂和力评价指标考虑了动载荷的相关性和空间重复性，评价车辆对道路的破坏更为合理［9］。95百分位四次幂和力评价指标理论道路破坏系数J定义为:

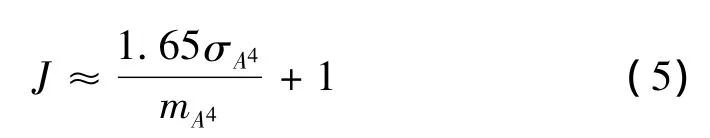
式中:σA4和mA4表示A4的标准偏差和均值，A4表示车辆各个轮胎动载荷的四次幂之和。

为了兼顾平顺性和道路友好性，需使总加权加速度均方根av和道路友好系数J均较小。由于目标有两个，可采用线性加权和法将多目标优化问题转化为单目标优化问题，由于各目标数值相差较大，先将各子目标函数进行无量纲归一化处理，再对各子目标函数进行线性加权处理，故综合性能指标表述如下:

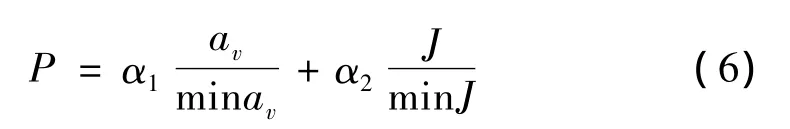
式中:α1与α2分别为平顺性与道路友好性目标函数的权重，满足归一性及非负条件，可根据各子目标函数的极小值信息应用 α 方法确定权重［10］，得 α1=0.52，α2=0.48。

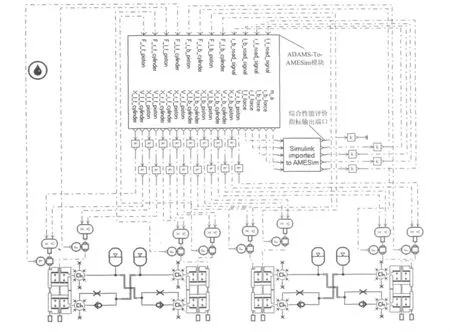
图4 基于AMESim/ADAMS/Simulink的整车连通式油气悬架联合仿真模型Fig.4 Co-simulation model of whole vehicle interconnected hydro-pneumatic suspension based on AMESim/ADAMS/Simulink

3.2 设计变量及约束条件

对于油气悬架系统而言，悬架缸为承载元件，蓄能器为刚度元件，阻尼、单向阀和管路为阻尼元件。由于车身重量确定，故悬架缸尺寸一般固定，加入单向阀是为了提高平安比，故参数无需调整，实际工程车辆中，管路布置安装位置确定，所需长度一般固定，变化不大，故参数也无需调整，综上分析，蓄能器的初始充气压力与总容积、阻尼孔径、管路通径可进行调整，即相应的调整了刚度系数和阻尼系数，进而调整了悬架的平顺性和道路友好性，故这四个参数为设计变量，依据工程实际，变量的初值及设计范围如表3所示。

表3 设计变量的优化初始值及变量范围Tab.3 Initial value and variable range of design variables

为了保证车辆行驶安全性，悬架的动行程是受悬架缸结构限制，由于车辆出厂设置时，悬架缸处于中位，故约束如下:

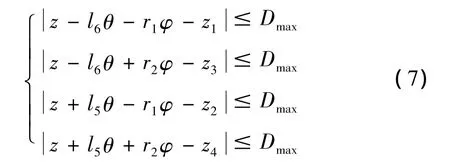
式中:Dmax为允许的最大动行程为175 mm。

4 联合仿真及遗传算法优化

4.1 Adams/Simulink/AMESim联合仿真

联合仿真方式采用以AMESim仿真平台为主，将Adams与Simulink模型经过编译后成为AMES-im识别的模块插入AMESim模型中如图4所示，联合仿真模型建立过程如下:第一，在AMESim中建立整车连通式油气悬架液压系统仿真模型，将悬架缸活塞杆和套筒的力信号导出输入到ADAMS-To-AMESim模块中;第二，在ADAMS中建立力驱动和取值函数将AMESim产生的力信号传输给ADA-MS构件即相应悬架缸活塞杆和套筒，同时，ADA-MS将经过计算得到各悬架缸活塞杆和套筒的位置和速度信号传输给AMESim中的悬架缸活塞杆和套筒如图4所示;第三，在Simulink中建立四轮相关路面输入的仿真模型得出路面时域信号，将其传输给ADAMS-To-AMESim模块中的路面信号，同时在ADAMS中设置直线驱动使相应轮胎以此时域信号上下运动，即仿真了轮胎通过C级路面的情况;第四，由于需要对平顺性和道路友好性评价指标进行计算分析，在ADAMS中建立了车身加速度和各轮胎受力信号输出，将此信号导入到Simulink中根据式(3)～式(6)建立好的计算模型，最终得出平顺性和道路友好性的综合性能评价指标，并在Simulink imported to AMESim的输出端口上输出［11］。

4.2 遗传算法优化

联合仿真平台设置好后，在AMESim/Design Exploration中建立蓄能器初始充气压力、蓄能器总容积、阻尼孔径、管路内径四个设计变量并设置变量范围，同时建立约束条件，取Simulink imported to AMESim模块的综合性能评价指标输出端口为优化目标，采用遗传算法进行全局优化分析。

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。遗传算法以决策变量的编码作为运算对象，直接以目标函数值作为搜索信息，可同时使用多个搜索点的搜索信息，且使用了概率搜索技术，以上这些特点使得遗传算法具有较强的鲁棒性，会使参数对搜索效果的影响尽可能的低。

对于连通式油气悬架平顺性和道路友好性的多目标优化问题，选择遗传算法各参数如下:种群规模为个体数50个，种群中个体被个体的复制率为80%，执行遗传算法的最大代数为20代，群体中离散型参数变异的概率为10%，变异幅值为0.8，产生初始种群后进行遗传迭代，计算出最优解［12，13］。

经过一段时间的联合仿真运算，最终计算出来的各参数优化值为:蓄能器初始充气压力为84.1 bar、蓄能器总容积为5.3 L、阻尼孔径为14.4 mm、管路内径为23.7 mm，各性能评价指标对比如表4所示。

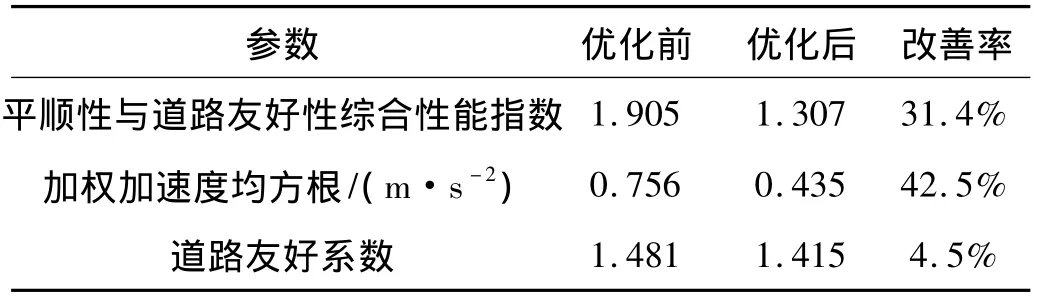
表4 优化前后性能指标对比Tab.4 Comparison of performance before and after optimization

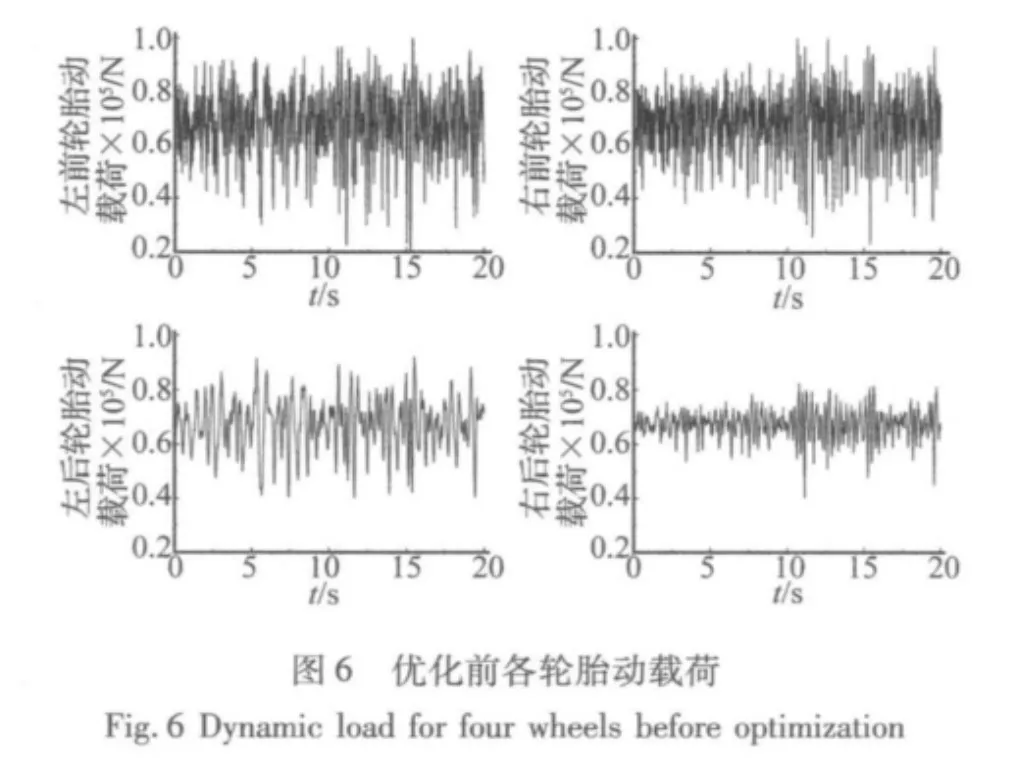
仿真得到的优化前后的车身加速度及各轮胎动载荷的时域信号对比如下:

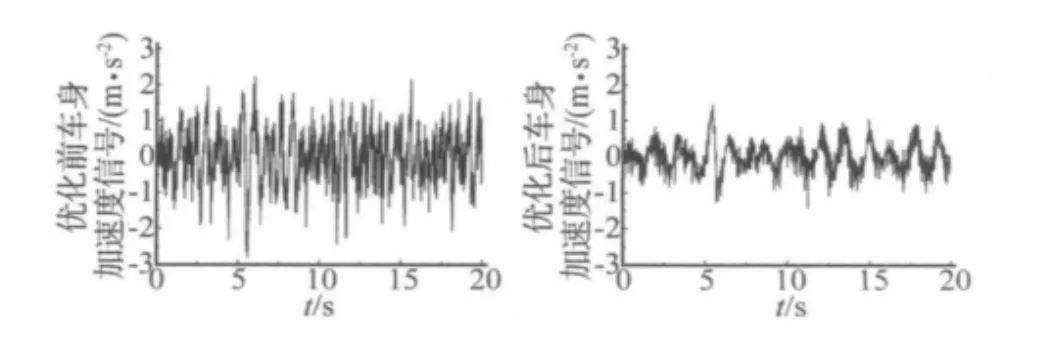
图5 优化前后车身加速度信号Fig.5 Acceleration of vehicle body before and after optimization

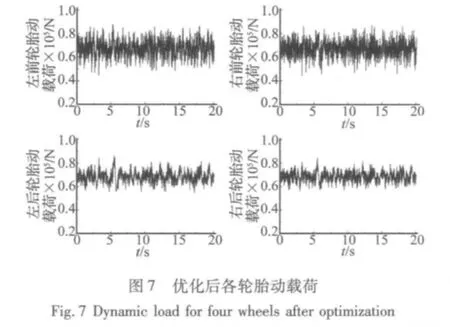
由于大型工程车辆最常行驶车速为60 km/h，故优化计算均以此速度为基础，但是为了分析所得优化参数在不同车速下的优化效果，可在不同车速下进行仿真计算分析平顺性和道路友好性的改善情况，整理如表5所示。

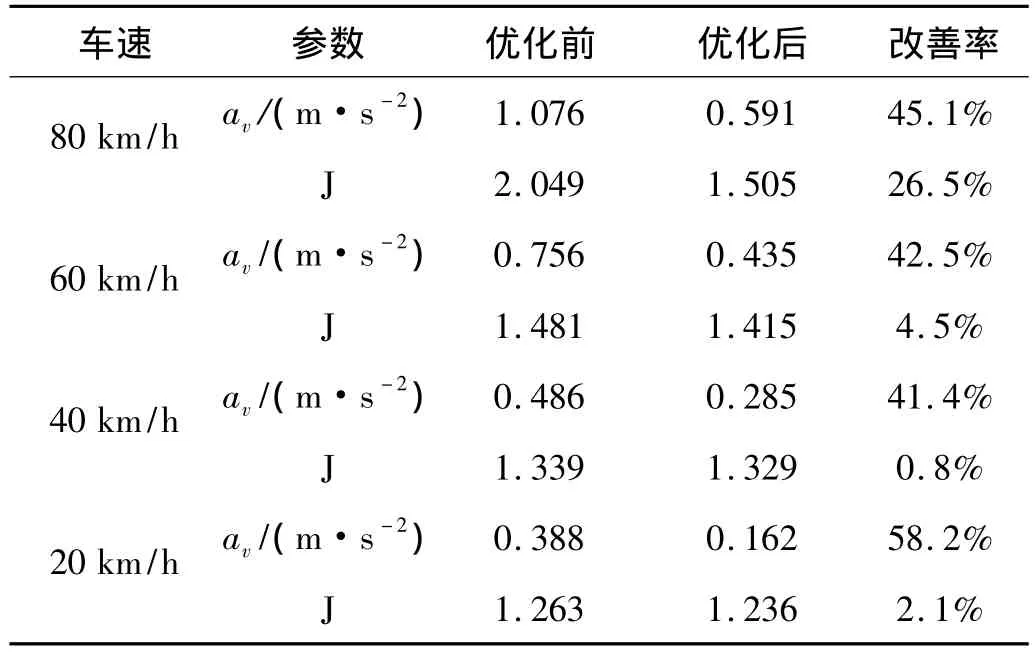
表5 不同车速下优化前后性能指标对比Tab.5 Comparison of performance before and after optimization at different speeds

由各图表可以看出，在车速为60 km/h情况下经过优化后车身加速度和各轮胎处的动载荷均有所减小，平顺性与道路友好性均有所改善，且在其他车速情况下平顺性与道路友好性也均有所改善，平顺性改善幅度均较大而道路友好性改善幅度均较小，可见经过优化后，能有效提高连通式油气悬架的性能，且悬架阻尼比经过仿真计算为1.2，也满足车辆设计的要求范围。

5 结论

(1)针对车辆平顺性和道路友好性，在深入分析整车连通式油气悬架数学模型基础上，建立了包括车辆结构、路面时域相关信号、液压系统在内的ADAMS/Simulink/AMESim联合仿真模型并进行多目标优化，采用AMESim遗传优化算法工具进行了优化分析。搭建的基于遗传算法的联合仿真平台不仅可以方便有效的找到最优参数，而且为今后五轴、七轴等多轴车辆的仿真提供了有效参考。

(2)在车速为60 km/h时，进行优化后的整车平顺性和道路友好性综合性能指数降低了31.4%，总加权加速度均方根值降低了42.5%，道路友好系数降低了4.5%，其它几种车速下平顺性均有大幅改善且道路友好性也均有小幅改善，对提高实际工程车辆的底盘性能有重要意义。

［1］邹 游，喻 凡，孙 涛.非线性油气悬架的平顺性仿真研究［J］.计算机仿真，2004，21(10):157 －159，110.

［2］Rideout G，Anderson R J.Experimental testing and mathematical modelling of the interconnected hydragassuspension system［C］.SAE Paper，2003 －01 －0312，2003.

［3］卢毅非.连接式油气悬架的特性分析［J］.工程机械，1995，26(4):11 －14.

［4］艾延廷，王 志，甘世俊，等.多自由度车辆模型半主动悬架模糊控制［J］.振动与冲击，2007，26(3):19－22.

［5］刘从臻，郭维俊，王芬娥，等.八自由度车辆模型传递函数研究［J］.甘肃农业大学学报，2006，41(3):113－117.

［6］刘 强，徐 斌，林 波.减小动载荷道路破坏的悬架参数研究［J］.哈尔滨工业大学学报，2002，34(6):832－837.

［7］吴明翔，陈 俐，张建武.路面检测车新型主动悬架LQG控制的研究［J］.振动与冲击，2009，28(9):125－129.

［8］张立军，张天侠.车辆四轮相关时域随机输入通用模型的研究［J］.农业机械学报，2005，36(12):29－31.

［9］Cole D J，Cebon D.Truck suspension design to mini-mize road damage［J］.Journal of Automobile Engineering，1996，210(2):95－107.

［10］吕彭民，和丽梅，尤晋闽.基于舒适性和轮胎动载的车辆悬架参数优化［J］.中国公路学报，2007，20(1):112－117.

［11］魏建华，杜 恒，方 向.基于ADAMS/Simulink/AMESim的连通式油气悬架道路友好性分析［J］.农业机械学报，2010，41(10):11 －17.

［12］王 涛.汽车悬架参数的多目标多标准决策优化［J］.农业机械学报，2009，40(4):27－32.

［13］王 涛，陶 薇.考虑随机因素的汽车悬架参数多目标稳健优化［J］.振动与冲击，2009，28(11):146－149.