大跨径铁路钢管混凝土系杆拱桥稳定性分析

季日臣，石明星

(兰州交通大学 土木工程学院，兰州 730070)

稳定问题是桥梁工程中经常遇到的问题，与强度问题有着同等重要的意义。随着桥梁跨径的不断增大，桥塔高耸化、箱梁薄壁化以及高强材料的应用，结构整体和局部的刚度下降，使得稳定问题显得比以往更为突出［1］。对于单线铁路钢管混凝土拱桥而言，由于桥梁宽度限制，采用大跨径必然导致宽跨比较小，稳定性在设计和施工中显得尤为突出，因此有必要对其进行深入研究［2］。本文以一孔跨度为136m的下承式钢管混凝土系杆拱桥为对象，对该桥进行了空间稳定性分析。

红柳林至神木西铁路专用线格丑沟特大桥位于红柳林至神木西新建铁路线上，为跨越格丑沟及204国道而设，主桥采用一孔136 m钢管混凝土系杆拱桥跨越。该桥为单线刚性系梁刚性拱桥，系梁与拱肋固接，整个结构为内部超静定外部静定。计算跨径L=136 m，全长139.6 m，拱轴线采用二次抛物线，矢跨比f/L=1∶5，矢高为27.2 m。拱肋采用外径110 cm壁厚18 mm的钢管混凝土截面，上下两拱肋中心距2.5 m，拱肋截面高3.6 m，上下拱肋之间采用厚14 mm的腹板连接。拱肋之间共设1组米字形横撑、6道K撑，每道横撑均为空钢管组成的桁式结构。全桥共设14对吊杆，吊点中心距8 m，每点吊杆为双根55－φ7平行钢丝束组成，冷铸镦头锚固，中心间距为50 cm。系梁采用预应力混凝土简支箱梁，横截面为单箱双室，高为2.8 m，端部加高至 3.3 m;梁顶宽11.2 m，底宽9.0 m.系梁两端设铸钢铰支座与桥墩相连，一端固定一端滑动。成桥效果图如图1，在全国在建的同类单线铁路系杆拱桥中跨度最大。

图1 成桥效果图Fig.1 Bridge effect figure

1 稳定分析方法

拱作为压弯结构，稳定问题是计算理论要研究的重要内容之一。对于系杆拱桥而言，拱是主要受压构件，稳定问题主要是针对拱的稳定。拱的稳定从失稳的性质上可以分为第一类稳定和第二类稳定。第一类稳定，即分支点失稳问题;第二类稳定，即极值点失稳问题［3］。

目前对拱桥的稳定分析以弹性理论(第一类稳定)为主，但在实际工程中，拱桥的稳定问题一般都表现为第二类失稳。本文首先对该桥进行第一类稳定分析，然后考虑非线性影响，对本桥进行第二类稳定分析，最后探讨拱桥稳定性影响因素。

本文用有限元平衡方程来表达第一类稳定问题的线弹性失稳的物理现象。在临界荷载下，结构线性屈曲平衡方程为:)

式中［K］为弹性刚度矩阵;［K］σ为几何刚度矩阵，它只与结构轴力有关;{Δu}为结构的位移，{ΔP}为结构的荷载增量。当结构在临界状态下，即使{ΔP}→0，{Δu}也有非零解，按线性代数理论，有:

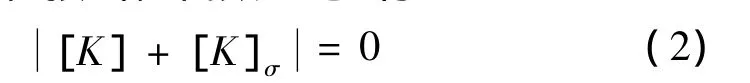
在小变形情况下，［K］σ与应力水平成正比。由于发生第一类失稳前满足线性假设，多数情况下应力与外荷载表现为线性关系，因此，若结构在某参考荷载对应的结构几何刚度阵为，临界荷载为{F}cr= λ，那么在临界荷载作用下结构的几何刚度矩阵为:

于是式(3)可写成:

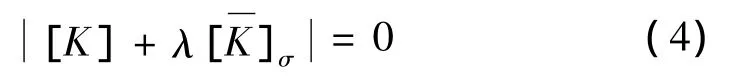
式(4)就是第一类稳定问题的控制方程，λ为荷载稳定系数，这样就将稳定问题转化为数学上求解特征值的问题，应用各种迭代方法，如逆矢量迭代法、子空间迭代法等都可以很方便地求解［4，5］。

从力学分析的角度看，第二类稳定问题分析桥梁结构极限承载能力的实质就是通过计入几何非线性和材料非线性对结构刚度矩阵的影响，求解平衡方程，寻找其极限荷载的过程。我们可以求出结构在受荷载全过程中荷载－位移(P－△)曲线。通常解决极值失稳问题采用荷载增量法［6，7］。整个结构的增量方程为:

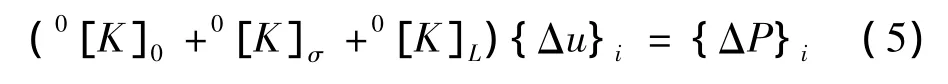
式中，0［K］0、0［K］σ和0［K］L分别为 t=0 时刻结构的弹性刚度矩阵、初应力刚度矩阵和初位移刚度矩阵;{Δu}i为第 i次加载{ΔP}i时产生的位移增量。

2 结构稳定分析

2.1 有限元模型

本文应用有限元分析软件MIDAS进行分析计算，该软件单元种类丰富，功能强大，基本上可以满足工程需要。因为本桥上部结构外部静定内部超静定，有限元分析时，只考虑上部结构。系梁、拱肋、横撑、K撑、横撑腹杆均采用梁单元模拟，其中，钢管混凝土拱肋哑铃型截面采用施工阶段联合截面，程序会根据各位置的刚度特性值以及材龄，计算联合后截面的特性值。系梁端部采用变截面梁单元模拟。吊杆用索单元进行模拟。计算模型节点总数为460个，梁单元为603个，索单元为28个，刚臂单元30个。有限元计算模型如图2所示。

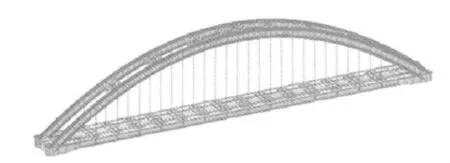
图2 空间有限元模型Fig.2 The three dimension finite element model

2.2 第一类稳定分析

本文考虑了两种工况，第一种是只有恒载作用的情况，第二种是恒载+活载不利布置的情况(活载按《铁路桥涵设计基本规范》(TB10002.1－2005)规定的中－活载)。在第一种荷载工况下结构的临界荷载系数为5.8，在第二种荷载工况下结构的临界荷载系数为5.1，限于篇幅，在此仅给出恒载+活载不利布置下格丑沟特大桥前五阶屈曲模态见图3及屈曲计算结果见表1。

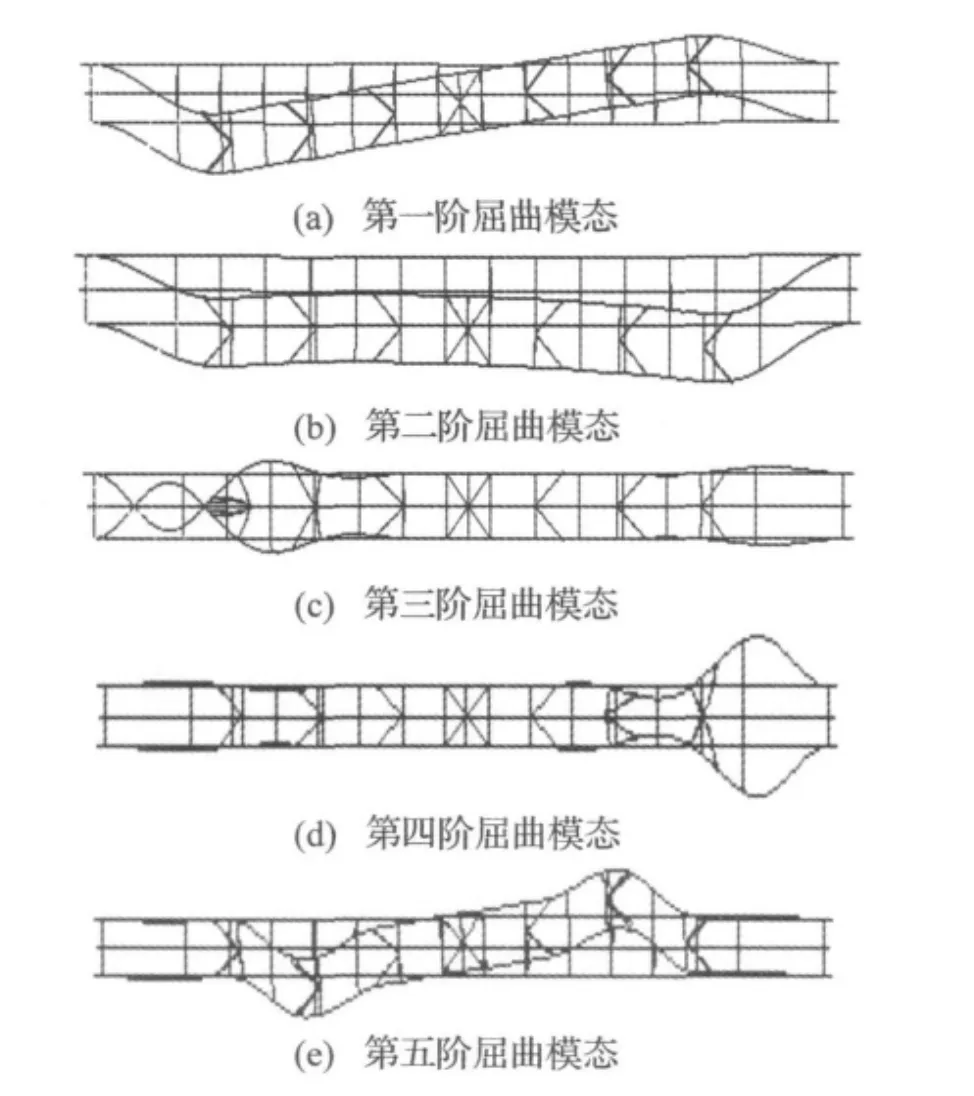
图3 拱桥前五阶屈曲模态Fig.3 The first five buckling modes of arch

表1 屈曲计算结果Tab.1 The result of arch buckling

2.3 第二类稳定分析

本文拟在上述第二种荷载工况下，分三种情况对本桥进行第二类稳定分析，通过比较分析非线性对钢管混凝土拱桥稳定的影响以及哪一类非线性对本桥的稳定性影响更大。在考虑材料非线性时假设钢管和混凝土之间粘结较好，没有相对滑移和变形;考虑钢管对混凝土的套箍作用，将钢管混凝土视为单一的组合材料;从加载到失稳破坏整个过程中，平截面假定成立;截面形状与面积在变形前后不发生变化［8］。计算结果见表2。

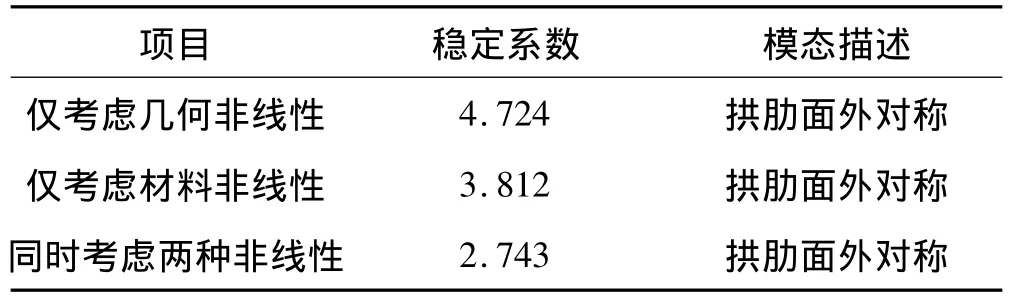
表2 第二类稳定计算结果Tab.2 The result of the second stability

从表2中的数据可以看出，在三种情况下，结构的稳定系数均小于相应工况下结构弹性失稳屈曲系数5.092，并且仅考虑几何非线性时稳定系数降低了7.23%，仅考虑材料非线性时稳定系数降低了25.14%，同时考虑两种非线性时稳定系数降低了46.13%，由此可见在计算大跨径钢管混凝土系杆拱桥的稳定时，几何非线性和材料非线性的影响是不可忽略的，从结构工作性能来看，既考虑几何非线性又考虑材料非线性的计算方法更加符合实际，计算结果也更为可靠［9］，另外，对于本桥而言，材料非线性对稳定的影响大于几何非线性。

为了考察钢管混凝土拱肋在非线性影响下的的受力及变形情况，在拱肋上加载竖向均布力，加载位置为拱肋与吊杆的连接点。通过计算得出结构在非线性影响下的极限荷载及拱肋各控制截面的横向位移和竖向位移见图4及表3。

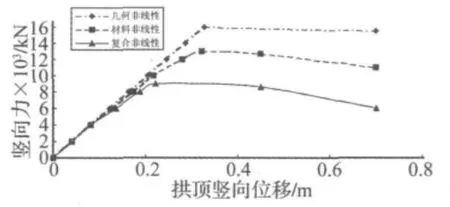
图4 拱顶截面的荷载－竖向位移曲线图Fig.4 Load-vertical displacement curve of the vault section

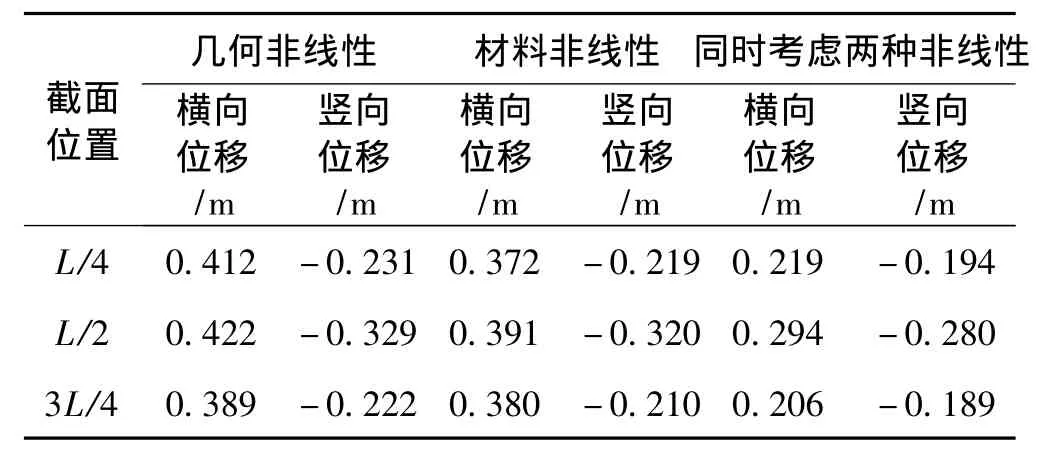
表3 拱肋达到稳定极限承载力时控制截面的位移Tab.3 Displacement of each controlling section when the arch ribs reach the ultimate loads

由图4可以看出，本桥在只考虑几何非线性时节点的极限荷载为16000 kN，只考虑材料非线性时节点的极限荷载为13000 kN，同时考虑两种非线性时节点的极限荷载为9000 kN。由此可见，只考虑几何非线性或材料非线性对拱肋承载力的影响时，钢管混凝土拱肋的极限承载力明显大于同时考虑两种非线性时拱肋的极限承载力，并且材料非线性对拱肋极限承载力的影响大于几何非线性的影响，在同时考虑了两种非线性时，拱肋的极限承载力明显下降，说明考虑复合非线性计算的结果更接近实际。

由表3可以看出，对于拱肋的竖向位移或横向位移，不论考虑哪种非线性影响，均为拱顶截面最大，L/4和3L/4截面近似相等。对于各控制截面而言，不论考虑哪种非线性影响，均表现为横向位移大于竖向位移，更进一步说明了拱肋的面外刚度小于面内刚度，失稳主要表现为面外失稳。分别考虑几何非线性和材料非线性时位移相差不大，考虑了复合非线性时，各控制截面在拱肋达到极限荷载时的横向位移和竖向位移均明显减小。

3 钢管混凝土拱桥稳定性影响因素

根据拱桥稳定计算理论和许多文献的观点［10］，对于钢管混凝土双肋拱桥，横撑的布置形式、拱肋内倾角和主拱的矢跨比等均对整体稳定性有较大影响。本文主要针对以上三种影响因素进行比较分析。

3.1 横撑布置形式的影响

本桥共设七道横撑，拱顶为一道米字形横撑，拱顶两侧各对称布置三道K型横撑，每道横撑均为空钢管组成的桁式结构。本文拟采取Ⅰ型横撑(横撑位置不变)和无横撑形式与原体系作比较来研究横撑布置形式对稳定性的影响。限于篇幅，在此仅给出三种体系下第一阶屈曲模态见图5及屈曲计算结果见表4。

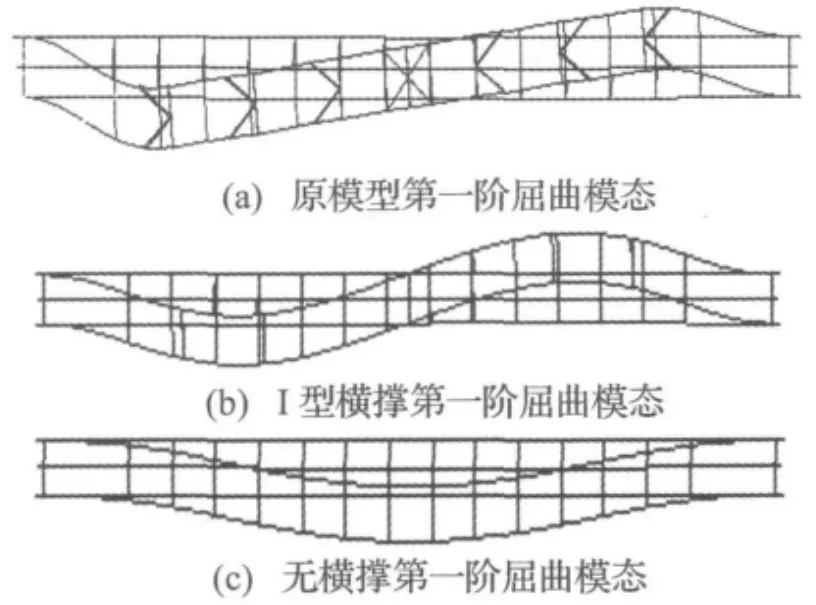
图5 三种体系的第一阶屈曲模态Fig.5 The first buckling modes of three system

表4 屈曲计算结果Tab.4 The result of arch buckling

由表4可以看出，在三种横撑布置形式中，K型横撑的稳定系数最高，且满足一般要求，I型横撑和无横撑形式的稳定系数均不满足一般要求，并且结构的失稳模态也由面外反对称失稳变为面外对称失稳。

由于影响拱桥横向稳定最直接的因素在于拱圈的抗弯刚度，而拱肋间横向连接构件(即横撑)对拱圈的抗弯刚度起关键性作用，I型横撑对提高拱圈稳定性的作用不明显，而K型横撑对提高拱圈横向稳定的效果较I型横撑要好的多，所以，在不改变单根弦杆和腹杆刚度的情况下，通过改变横撑型式可以达到改变横撑整体刚度的目的，对拱桥整体稳定性的提高是明显的。因此合理横撑形式的选择对拱桥的整体稳定性意义重大。

3.2 拱肋内倾角的影响

具有一定内倾角的提篮拱肋的结构具有更高的抗侧倾能力，但拱肋的内倾角有其合理的取值，不是越大越好。本文分别对拱肋在内倾角为0°、2°、4°和6°时进行建模，以研究结构在不同内倾角时的稳定系数，分析结果如图6所示。

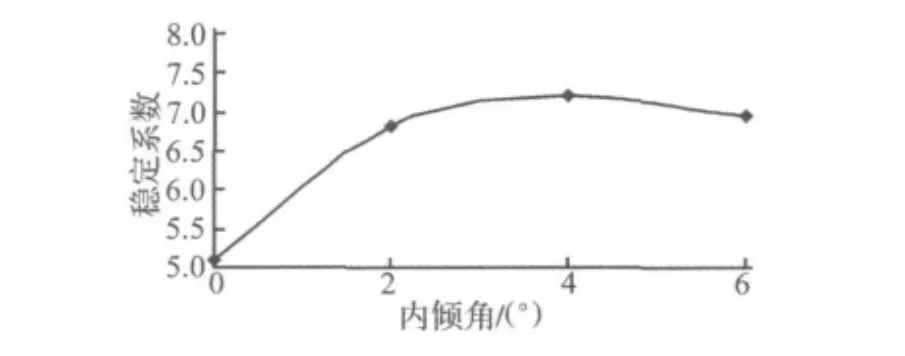
图6 结构稳定系数随拱肋内倾角的变化图Fig.6 Variation figure of the structure stability factor along with the arch rib inclination angle

由图6可以看出，拱肋内倾角变化时，结构的横向稳定系数也随着变化。内倾角在0°～4°变化时，结构的稳定系数随着内倾角的变大而变大;当内倾角大于4°时，结构稳定系数随内倾角变大而减小。结论和文献［11］对窄桥的最优内倾角的合理取值结论相似。

3.3 矢跨比的影响

矢跨比是拱桥拱轴线型的一个重要设计参数，结构的受力、桥梁的施工方法以及桥梁的整个造价等都与矢跨比密切相关，同时，结构与周围环境是否和谐协调、整个桥梁的视觉效果都与矢跨比的大小有密切的关系。本桥计算跨径为136 m，矢跨比为1/5。本文保持其它条件不变，通过建立7种矢跨比(1/4、1/4.5、1/5、1/5.5、1/6、1/6.5、1/7)的有限元模型来分析对比其对桥梁结构稳定性的影响，分析结果如图7所示。

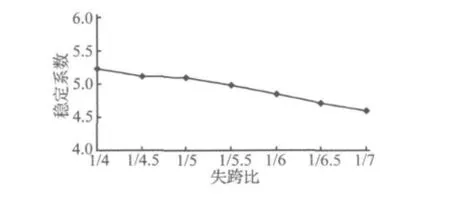
图7 不同矢跨比时结构稳定系数的变化图Fig.7 Variation figure of the structure stability factor under the different ratio of height to span

由图7可以看出，随着矢跨比的减小，稳定系数也呈现出减小的趋势，如果将矢跨比选择的偏大，虽然可以使得桥梁的稳定性提高，但是造成拱弧较长，拱肋的材料用量也将增大，从而增加了桥梁造价，相反，如果将矢跨比选择的偏小，虽然可以使得拱弧变短，拱肋的材料用量减小，从而减小了桥梁造价，但是这样会使得桥梁的稳定性降低，同时矢跨比过大或者过小都会造成视觉效果上的不协调，因而拱桥的矢跨比有其合理的取值范围。因此，从施工、结构受力和视觉效果上考虑，矢跨比为1/5时是相对较合适的，这也是拱桥设计中常采用的矢跨比值。

4 结论

(1)格丑沟特大桥主桥系杆拱的弹性屈曲系数大于一般要求(4～5)，弹性稳定满足要求，由于格丑沟特大桥的桥面系刚度较大，桥梁的失稳主要表现为拱肋的面外失稳。

(2)考虑非线性的影响下，结构的稳定系数均小于相应工况下结构弹性失稳屈曲系数，由此可见在计算大跨径钢管混凝土拱桥的稳定时，几何非线性和材料非线性的影响是不可忽略的。通过比较第二类稳定分析结果发现，材料非线性对本桥稳定的影响大于几何非线性。

(3)本文比较了三种不同形式的横撑对桥梁稳定性的影响，指出K型横撑的稳定系数最高，因此在横撑设计时应优先考虑K撑。

(4)本文比较了4种拱肋内倾角对桥梁结构稳定性的影响，计算结果表明，拱肋内倾角变化时，结构的横向稳定系数也跟着变化。内倾角在0°～4°时，结构的稳定系数随着内倾角的变大而变大;当内倾角大于4°时，结构稳定系数随内倾角变大而减小，建议结构优化时应优先考虑提篮拱。

(5)本文通过建立7种矢跨比的有限元模型来分析对比其对桥梁结构稳定性的影响，计算结果表明，随着矢跨比的减小，稳定系数也呈现出减小的趋势。

［1］项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001:262－280.

［2］范金军，邱文亮，张 哲.丹东月亮岛大桥施工过程中的稳定性分析［J］.公路，2003(5):1 －3.

［3］刘世忠，欧阳永金，沈 波.钢管系杆拱桥的整体稳定性及自振特性分析［J］.甘肃科学学报，1994，6(1):28－35.

［4］李国豪.桥梁结构稳定与震动［M］.北京:中国铁道出版社，1996:386－403.

［5］Ren W X，Zhao T，Issam E.Analysis of steel arch bridge［J］.Journal of Structural Engineering，2004， 130(1):1022－1031.

［6］Kim S E，Choi S H，Ma S S.Performance based design of steel arch bridges using practical inelastic nonlinear analysis［J］.Journal of Constructional Steel Research，2003，59(1):91－108.

［7］Nazmy A S.Stability and load-carrying capacity of threedimensional long-span steel arch bridges ［J］.Computers＆Structures，1997，65(6):857 －868.

［8］韩林海.钢管混凝土结构［M］.北京:科技出版社，2000:80－221.

［9］谭红霞，陈政清，封周权.刚构－单肋拱组合桥梁的稳定性研究［J］.振动与冲击，2008，27(12):122 －125.

［10］吴尚杰，郑振飞.大跨径钢管混凝土肋拱桥侧向稳定性的有限元分析［J］.华东公路，1996(6):23 －26.

［11］潘盛山，张 哲，黄才良.下承式X型拱肋内倾角度对横向稳定性的影响研究［J］.大连理工大学学报.2008，48(6):845－850.