等效力控制方法在连梁阻尼器拟动力子结构试验中的应用

周大睿，许国山，吴 斌，滕 军，马伯涛

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090;2.哈尔滨工业大学 深圳研究生院，深圳 518055)

拟动力试验方法(又称联机试验方法)是将计算机与加载作动器联机求解结构运动方程的方法，目的是真实模拟结构在地震作用下的反应。拟动力试验在过去几十年中得到了广泛的研究与应用［1－6］。拟动力试验方法需要依靠逐步积分方法求解结构运动方程。逐步积分方法分为显式积分方法和隐式积分方法。隐式方法相对于显式方法的优点是通常为无条件稳定的方法，计算精度也通常优于显式方法。然而隐式方法需要迭代求解非线性方程。

为了避免复杂耗时的迭代过程，Wu等人［7］提出了应用反馈控制求解非线性方程的实时子结构试验等效力控制方法(EFCM)。Wu等人［8－12］又进一步通过多自由度结构和非线性结构试验证明了此方法的有效性。虽然这种方法是由实时子结构试验提出的，它对于拟动力试验同样适用。文献［13］通过弹簧试件的试验初步证明了等效力控制方法对于拟动力试验的有效性，还需要进一步通过实际结构检验此方法的有效性。

剪力墙结构的抗侧能力非常好，在大型复杂结构中有较好的应用前景。为了增强剪力墙连梁的耗能能力，同时解决连梁配筋难问题，滕军等人［14－16］提出了耗能连梁方案，在连梁上附着连梁阻尼器或用连梁阻尼器替换连梁。然而，这种结构的抗震性能还需要通过试验检验。

本文用等效力控制方法完成此结构的拟动力子结构试验来检验等效力控制方法有效性，同时检验此结构的抗震性能。

1 等效力控制方法原理

文献［7］以平均加速度法为例介绍了等效力控制方法原理。当数值子结构的阻尼力为线性时，实时子结构试验等效力控制方法的动态平衡方程为:

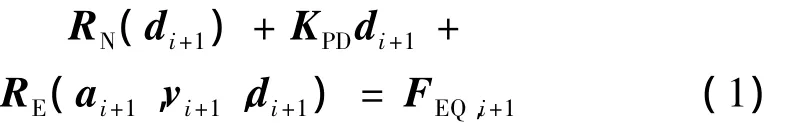
其中:

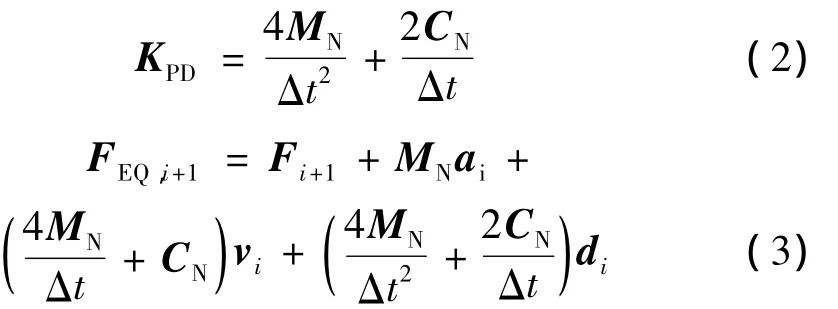
式中角标N表示数值子结构，角标E表示试验子结构;d、v、a分别为位移、速度、加速度向量，M、C分别为质量、阻尼矩阵，R为反力向量，F为外荷载向量，Δt为积分时间间隔。式(1)为关于di+1的非线性方程，方程左边由数值子结构静反力RN(di+1)、拟动力反力KPDdi+1和试验子结构反力RE(ai+1，vi+1，di+1)三部分构成;右边FEQ，i+1可以理解为施加在混合体系上由式(3)确定的等效外力。因此，方程(1)的解可以看作是混合体系在等效外力FEQ，i+1作用下的位移。这个位移可以通过在混合体系上施加等效力命令FEQ，i+1，应用反馈控制方法得到。

采用隐式逐步积分方法的实时子结构试验可以通过图1所示的等效力控制方法完成。在每一个采样点上，等效力命令 FEQ，i+1与等效力响应(反馈量)F'EQ，i+1(t)的偏差eEQ(t)通过等效力控制器和力－位移转换矩阵CF转化为位移命令dci+1(t)，以发给试验加载系统。d'i+1(t)是试验子结构在位移命令下的位移反应，RE［d'i+1(t)］分别为试验子结构反力、数值子结构静反力和拟动力反力。等效力控制器的作用是促进等效力响应跟踪等效力命令。在每个积分时间间隔内，如果等效力响应可以分很时好间地间跟隔踪末其点等将成效为力方命程令(，1则)位的解移。命令在积

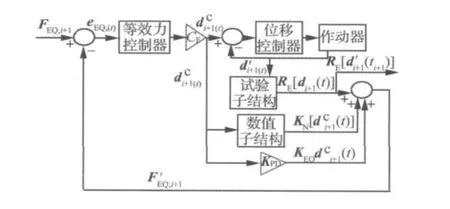
图1 等效力控制方法原理图Fig.1 Block diagram of equivalent force control method

反馈控制系统通常会存在控制误差，这将使在积分时间间隔末点测量的位移反应不是方程(1)的精确解。为了解决这个问题，积分时间间隔末点位移di+1最好由测得的RE［d'i+1(ti+1)］和计算的代入方程(1)计算得到，而不是直接取为测量的值。另外，对于数值子结构和试验子结构共用自由度的情况，两个子结构应该含有相同的位移、速度和加速度，因此应该用作动器位移响应d'i+1(t)计算共用自由度上的数值子结构静反力和拟动力反力。

虽然等效力控制方法是由实时子结构试验提出的，它同样可以应用到拟动力试验中。拟动力试验等效力控制方法与实时试验等效力控制方法的主要区别在于试验子结构的反力只与位移相关，以及每步等效力命令可以运行足够长的时间(如100Δt)以使等效力响应能很好地跟踪其命令。因此，拟动力子结构试验等效力控制方法应该具有与实时子结构试验等效力控制方法相同的稳定性和稳态误差。

文献［7－9］研究了采用比例－微分等效力控制器的等效力控制方法。文献［7，8］研究表明:对于线弹性结构试验，当CF=1/(KN+KPD+KE)时，增加前馈增KF=(1+KP)/KP后反馈控制系统在单步阶跃等效力命令输入下的响应没有稳态误差;当系统中各参数均选正值时，反馈控制系统的稳定条件总能满足。文献［9］又进一步研究表明:对于非线性结构试验，当，KS为结构割线刚度)时，用结构的起始刚度计算力－位移转换系数就能得到非常满意的结果;否则，必须准确估计其刚度(如上一步割线刚度)才能得到好的结果。

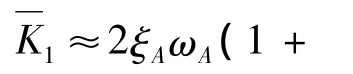
2 结构模型及试验方法

剪力墙结构的抗侧能力很好，适宜用于建造高层结构，目前备受工程师所青睐。对剪力墙连梁的研究主要集中在通过改变连梁配筋来满足概念设计，但是这种做法收效甚微，并且大大增加了设计和施工难度，目前工程应用较少。也有一些研究基于剪力墙结构属于弯曲变形结构，研究者将一片墙中间做剖开处理形成相邻的两片墙，在两片墙间做耗能件、摩擦件;该方法有其合理性，但施工较麻烦，并且连接耗能件相对刚度很大的墙片能否起到实质性的作用还不确定，目前尚未普及。为此，滕军等人［14，15］提出了耗能连梁方案，通过在连梁上附着连梁阻尼器或用连梁阻尼器替换连梁，增强连梁的耗能能力，同时解决连梁配筋难问题。该阻尼器能够在连梁中充分发挥剪切耗能能力，有效耗散结构振动能量。

本文选一个简单的单片双肢剪力墙结构作为算例。选12层单片双肢剪力墙模型，层高3.3 m，楼板厚0.1 m。两个墙肢宽度均为2 m，连梁截面高度0.7 m，跨度2 m。将所有墙体厚度及连梁宽度均取为0.2 m，该墙片承载楼板宽度取为0.6 m。考虑结构荷载转换为质量，混凝土材料密度取为3.29×103kg/m3，楼板密度取为2.5 ×104kg/m3。

以上述双肢剪力墙模型为目标，在每层连梁两侧附着一个阻尼器，阻尼器和连梁一起承受弯矩和剪力，详细构造请参见文献［16］。在水平荷载作用下，双肢剪力墙的墙肢产生弯曲变形，从而使连梁左右两端产生转角，使连梁阻尼器产生剪切变形。当剪切变形很小时，阻尼器不参与耗能，仅提供初始刚度，提高连梁的承载力;否则，阻尼器率先进入塑性屈服，耗散振动能量。

为了试验方便，假定连梁和墙肢处于线性状态，将此结构简化为单自由度(SDOF)结构，并将所有阻尼器的功用“集成”后附加到单自由度简化结构上。将简化单自由度体系的质量取为原结构质量一半。采用刚度法确定简化单自由度体系的刚度。考虑到阻尼器的工作位移为连梁两端的剪切位移，所以在应用刚度法时，将在顶部施加单位位移得到的“水平反力”与“连梁两端剪切位移”的商作为简化单自由度体系的等效刚度。取等效阻尼比为5%。关于阻尼器功效的等效，假定阻尼器作用力能使结构产生虚位移δu，以此虚位移相等为目标，将阻尼器作用力等效成简化单自由度体系的等效恢复力。经分析得到，此等效恢复力与试验中阻尼器的作用力相等。模型参数详细的推导过程参见文献［15］。在另外一篇文章中用ABAQUS软件对原12层结构进行了数值模拟并通过比较验证了单自由度简化结构模型的有效性，本文不再做详细介绍。

结构的等效模型见图2。此单自由度简化模型参数取为 MN=7.5×104kg、KN=2.49 ×107N/m、阻尼比为5%。试验子结构为文献［16］中的H10A系列连梁阻尼器。

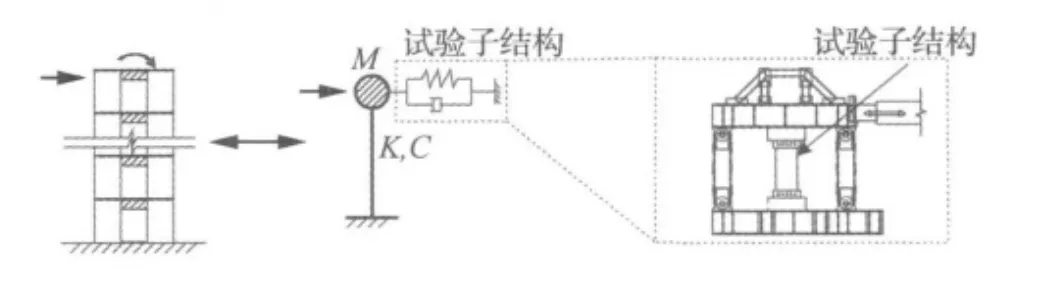
图2 结构模型等效Fig.2 Equivalent SDOF model of the structure

本文连梁阻尼器拟动力子结构试验在哈尔滨工业大学结构与抗震实验中心完成。图3为试验装置图，图4为试件照片［16］。试验设备主要有加载系统、采集系统、和四连杆试验架三个部分。通过四连杆试验架对连梁阻尼器施加法向的剪切荷载，用于模拟该类阻尼器在剪力墙结构连梁位置的实际受力工况。加载设备采用液压伺服作动器，控制器采用MTS控制系统(包括 FlexTest GT控制系统和 MTS793.10软件系统)［17］。本文以下试验将采用比例－积分等效力控制器，并且用结构起始刚度计算力－位移转换系数CF。

图3 试验架构成Fig.3 Construction of testing frame

图4 连梁阻尼器试件照片Fig.4 Photo of the coupling beam damper specimen

应用等效力控制方法试验时执行过程如下:

① 确定等效单自由度结构的起始条件。结构的质量、刚度、阻尼，结构的起始位移、速度、加速度，积分时间步长。确定试验子结构阻尼器出力与等效单自由度结构中阻尼器出力的关系;

② 在每个积分时间步(如第i+1步)的起始点，将上一步的信息带入式(3)计算这一时间步的等效力命令 FEQ，i+1;

③ 将此等效力命令作为图1所示的等效力反馈控制系统的输入。在每个采样点上计算 eEQ(t)、，测量阻尼器的作用力并将其转换为等效结构中阻尼器作用力，然后计算，直到积分时间步末点;

④ 在积分时间步末点，测量试验子结构反力RE，并将其转换为等效结构中阻尼器作用力，根据此反力和计算得到的数值子结构静反力RN带入到式(1)中计算修正后的位移di+1;

⑤ 将di+1带入平均加速度法的假定，求解相应时间步的加速度ai+1和速度vi+1;

⑥ 重复步骤②至⑤，直到试验结束。

3 试验结果分析

分别对此结构进行了El Centro和Taft地震记录激励下的拟动力子结构试验。两种地震波的峰值加速度分别为 35gal、140gal、220gal、620gal。试验中，积分时间间隔均取0.005 s，采用比例－积分等效力控制器，用起始刚度计算力－位移转换系数。

图5为此结构在峰值加速度为35gal的Taft地震记录激励下的试验结果。其中结构起始位移和速度为零，等效力控制器参数为KP=1.25、KI=15/s。为了显示连梁阻尼器的控制效果，由中心差分法纯数值模拟得到的无连梁阻尼器时的结果也列入图5(a)中。从此图可以看出等效力控制方法试验结果的位移幅值比数值模拟得到的无连梁阻尼器时的结果小很多，表明阻尼器起到了很好的控制作用。图5(b)为相应的等效力响应，从此图可以看出等效力响应能很好跟踪等效力命令，意味着试验结果是精确的。图5(c)为相应连梁阻尼器试件的滞回曲线，从此图可以看出连梁阻尼器基本成线性。连梁阻尼器主要是刚度贡献，提高连梁承载力。

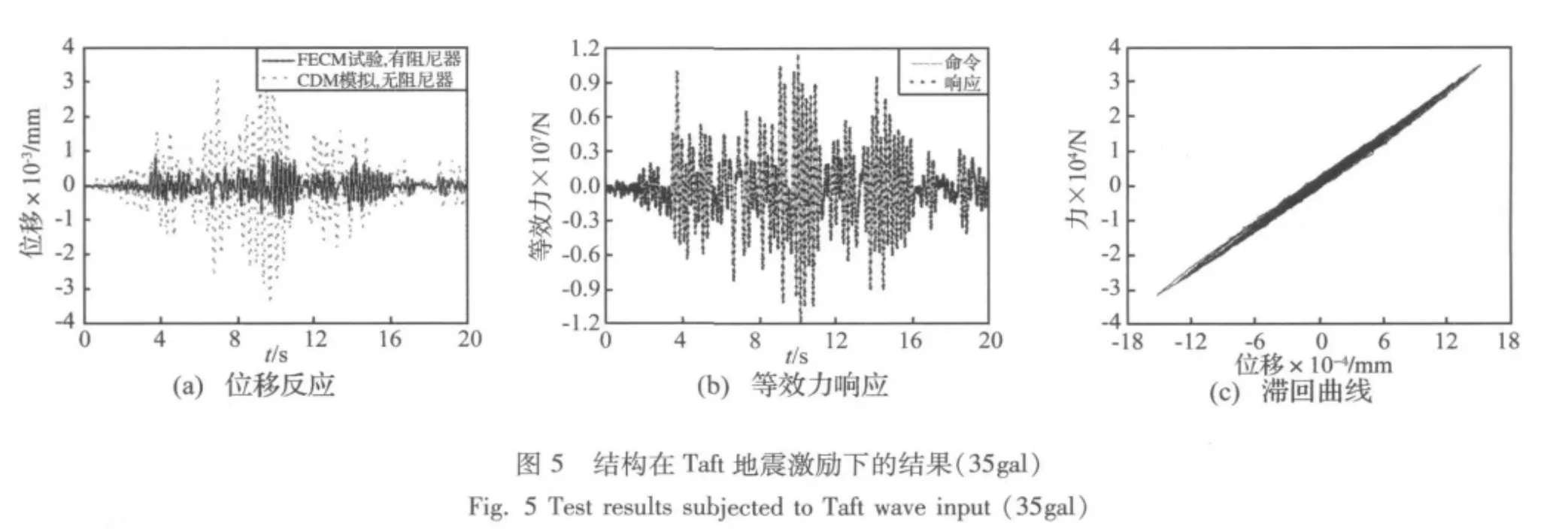
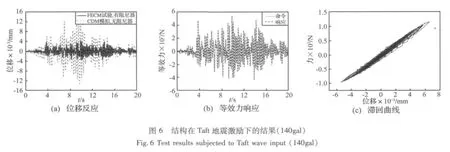
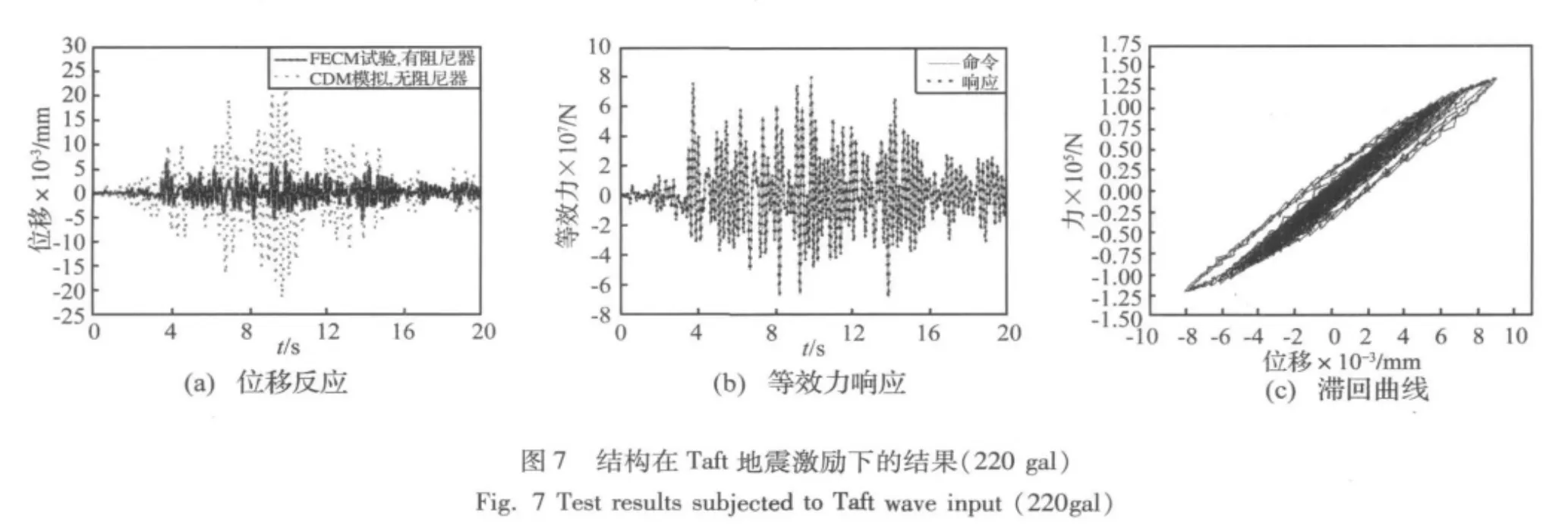
图8 结构在Taft地震激励下的结果(620gal)Fig.8 Test results subjected to Taft wave input(620gal)

图6、图7和图8分别为此结构在峰值加速度为140gal、220gal、620gal的 Taft地震记录激励下的试验结果。由这些图可以得到与图5相似的结论。值得说明的是，随着地震加速度幅值增大，连梁阻尼器的滞回曲线更加饱满。这表明连梁阻尼器起到支撑作用同时，还有效地通过滞回消耗地震能量。此结构在El Centro地震激励下也有相同的结论。

4 结论

本文成功应用等效力控制方法完成了连梁阻尼器的拟动力子结构试验，检验了其对双肢剪力墙结构的减震效果。研究结果表明:通过合理选取等效力控制器参数和力－位移转换系数，等效力控制方法具有很好的稳定性和精度;连梁阻尼器对双肢剪力墙结构的反应有很好的控制效果。

［1］Hakuno M，Shidowara M，Hara T.Dynamic destructive test of a cantilever beam，controlled by an analog-computer［M］.Transactions of the Japan Society of Civil Engineering，1969，171.

［2］黄 靓，施楚贤，刘桂秋，等.MDOF子结构拟动力方法在复杂高层结构抗震试验中的应用研究［J］.土木工程学报，2006，39(12):23－32.

［3］蔡新江，田石柱，王大鹏，等.FRP加固桥梁RC短柱拟静力及网络拟动力试验［J］.建筑结构学报，2009，30(2):125－135.

［4］范云蕾，肖 岩，郭玉荣，等.多层框架结构远程协同拟动力试验方法研究［J］.湖南大学学报(自然科学版)，2009，36(4):19－23.

［5］邱法维，潘 鹏，钱稼茹，等.建筑结构拟动力实验软件的开发与应用［J］.建筑结构学报，2000，21(5):22－32.

［6］王焕定，陈再现，王凤来，等.高阶单步拟动力试验算法［J］.工程力学，2008，25(11):14－19，26.

［7］Wu B，Wang Q，Shing P B，et al.Equivalent force control method for generalized real-time substructure testing with Implicit Integration ［J］. Earthquake Engineering and Structural Dynamics，2007，36:1127 －1149.

［8］许国山，吴 斌.弹性试件的实时子结构试验等效力控制方法［J］.振动与冲击，2010，29(5):101－105.

［9］许国山.实时子结构试验的等效力控制方法［D］.哈尔滨:哈尔滨工业大学，2010:18－75.

［10］许国山，吴 斌.采用比例－积分控制的实时子结构试验等效力控制方法［J］.工程力学，2009，26(9):251－256.

［11］许国山，吴 斌.采用等效力控制方法的非线性结构实时子结构试验［J］.振动工程学报.2010，23(3):119－124.

［12］Wu B，Xu G，Shing P B.Equivalentforce control method for real-time testing of nonlinear structures［J］.Journal of Earthquake Engineering，2011，15(1):143 －146.

［13］许国山，吴 斌.等效力控制方法在拟动力试验中的应用［J］.地震工程与工程振动，2010，30(2):79－85.

［14］滕 军，马伯涛，周正根，等.提高连肢墙抗震性能的连梁耗能构件关键技术［J］.工程抗震与加固改造，2007，29(5):1－6.

［15］滕 军，马伯涛，李卫华，等.联肢剪力墙连梁阻尼器的实验研究与仿真分析［C］.第十二届高层建筑抗震技术交流会论文集，北京，2009，10:562 －569.

［16］滕 军.结构振动控制的理论、技术和方法［M］.北京:科学出版社，2009.

［17］王倩颖.实时子结构试验方法及其应用［D］.哈尔滨:哈尔滨工业大学，2007:13－38.