纹理映射算法的改进研究

王 冉

(华北水利水电学院研究生处，河南郑州 450011)

纹理映射(Texture Mapping)技术是计算机图形学的重要组成部分，已经在解决真实感图形绘制问题中得到广泛应用。由于真实的景物表面存在着丰富的纹理细节，而这些纹理细节经常是区别各种具有相同外形的景物的依据，因此景物表面纹理细节的模拟在真实感图形合成技术中起着重要的作用。

纹理映射技术最早由 Catmull在1974年提出。Catmull首次提出纹理映射思想，实现了参数曲面上的纹理映射［1］。该方法通过对三维物体表面进行二维参数化，再将该参数值对应为纹理平面上的坐标值，从而得到相应的纹理值，即在物体表面生成了纹理图案。由于实际应用中大多数物体都表示为非参数化面片拼接而成的多面体，其表面的重新参数化相当困难，不能保证纹理在中介面上保持连续，或不产生扭曲变形现象，严重影响了真实感效果［3－5］。利用几何形体的知识，通过对样图进行合理的拉伸处理来修正物体两极处的汇聚现象，再用拼接融合技术保持物体表面的连续性，可得到良好的视觉效果。

1 构建三维曲面模型

在做纹理映射之前，要对被映射物体做几何模型建模，即进行三角化网格化剖分。其实三维物体表面网格是真实物体的近似模拟，表面网格由多个大小、形状、连接性并不一致的小三角形网格组成。为使几何模型更加平滑逼真，现采用气球算法对球体进行面绘制，并记录三角面片的顶点坐标和利用光照模型计算三角面片法向量，法向量是真实、准确显示物体表面的关键问题。

采用的光照模型为

其中，I为三角片的光强;Iα为环境的光强;Is为光源的光强;θ为三角片指向物体外部的法向量与光线的夹角。

气球算法［2］是一个基于动态可形变网格的分割算法，其思想是，模拟气球充气膨胀或者放气收缩的过程，构建一个大小形状可改变的网格结构，且网格中的顶点之间有边相连。

图1显示了利用气球算法计算得到的一个球体网格结构的过程，这里用到的是充气力而不是收缩力，所以网格从小到大变化。

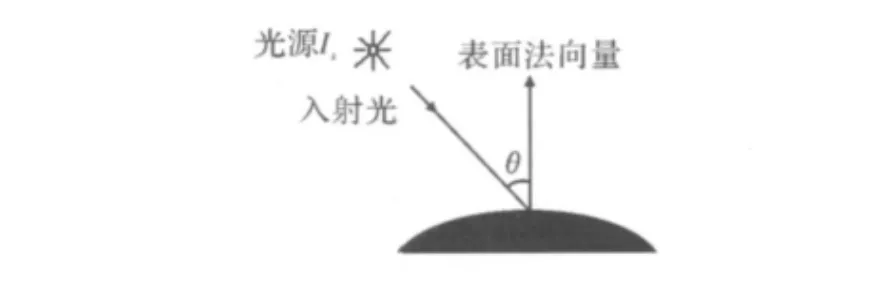
图1 光照模型

2 纹理图案的合成

随着基于像素的纹理合成技术的发展，现采用Ashikhmin算法对纹理图案进行合成。算法思想是:对当前待合成像素，搜索其有效邻域中像素，从而得到当前像素的候选位置列表。其最大特点是能够整块拷贝样图中的像素区域，且利用纹理的连续性进行加速，速度也比较快。但主要用于自然纹理的合成，无法用于结构性纹理的合成，图2(a)。合成的目的是保证样图与要映射的物体投影大小一致。

2.1 基于纹理图案的表面纹理绘制技术

在光滑曲面上添加纹理图案，比较严格的定义应该是:实际三维物体用二维平面真实表示，属于三维物体在二维平面真实感投影，其核心问题是映射，因此该问题可以简化为从一个坐标系到另一个坐标系的变换。实际上是涉及至少两个映射，即一个是从纹理空间到景物空间，通常称为曲面参数化;第二个映射是从景物空间到图像空间，即取景变换。通常，这两个变换被合成为一个变换。

例如，纹理图案定义在纹理空间中一个正交坐标系(u，v)中，曲面定义在景物空间的正交坐标系(x，y，z)中，它在参数空间(θ，φ)的表示为x(θ，φ)，y(θ，φ)，z(θ，φ)，那么在曲面上添加纹理将涉及在两个空间之间确定或指定一个映射函数。例如，从纹理空间到参数空间的映射为

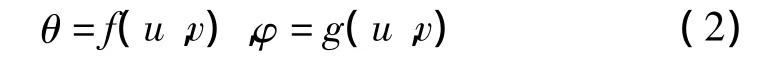
从参数空间到纹理空间的逆映射为

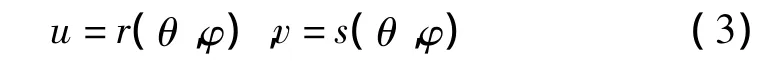
映射函数一般为一个线性函数，即

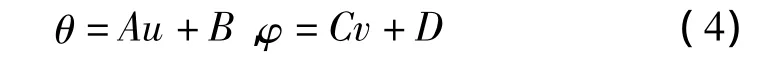
式中，常数A、B、C、D可由两个坐标系中的已知点之间的关系而获得。

2.2 曲面参数化

现对已建立的球体模型的表面进行参数化，讨论其参数r，θ，φ

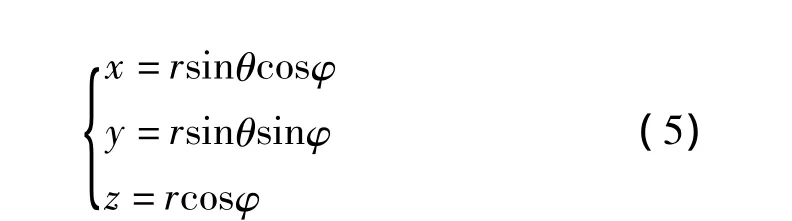
其中，r为球的半径;θ为与z轴的夹角且0≤θ≤π;为与x轴的夹角且0≤φ≤2π。三维到二维的映射，在正交坐标系中的定义为

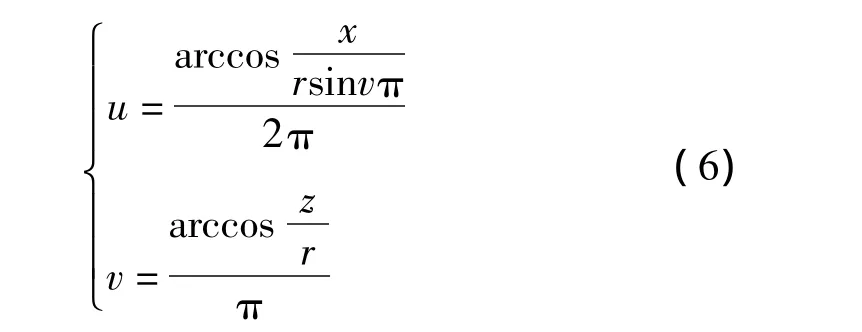
其中，0≤u≤1，0≤v≤1。

故重写式(7)曲面的参数定义方程，即得到二维到三维的映射

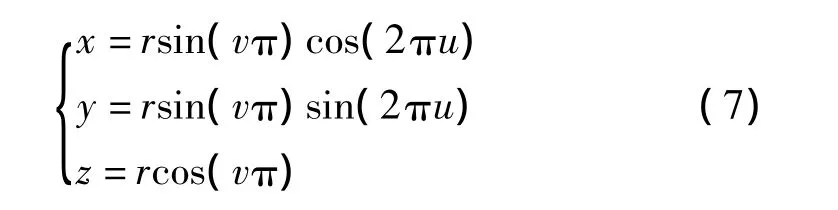
因此，球体表面上的点(x，y，z)就能与纹理中的点(u，v)一一对应，得到一个加纹理后的球面。

需要注意的是:

(1)球体展开后会发生形变，例如，球体中两点之间的距离不等于展开平面后两点之间的距离。

(2)在对曲面加纹理过程中存在两个特殊的点，即南极点和北极点，故要单独定义。

由图可见，用参数的方法进行纹理映射时，在球面的经线方向将不可避免地出现纹理接缝，并且在球的两极点存在纹理汇聚现象，即出现扭曲失真。

3 算法改进方法

3.1 纹理贴图的改进

最简单的改进方法就是让纹理贴图发生合理的形变，使得纹理贴图被垂直的映射到纬度线和水平的映射到经度线上，并定义与纬度线的夹角为θ，与经度线的夹角为φ。其中在映射到经度线上时，θ角按实际夹角处理，但φ需要变换，即φ=cosθφ，这样纹理贴图就可以发生合理的形变，使得球面两极处的纹理较均匀，如图4所示。

图5 改进规则

3.2 接缝的拼接与融合

当通过逆映射将纹理映射回3D表面时，会不同程度地出现拼接痕迹，即出现不连续现象。为减少人为的接缝，可以局部处理接缝的两侧，利用Alpha融合法移除视觉痕迹。步骤如下:

(1)对处理后的纹理贴图进行二维平面网格化处理。

(2)在接缝处对二维与三维平面网格进行三角匹配。

(3)匹配成功后，沿着边界进行三角形贴图。

(4)将接缝顶点进行初始化，令Alpha=0.5。

改进后的纹理映射效果如图6所示，可以看到，在拼接处的不连续现象明显得到改善。

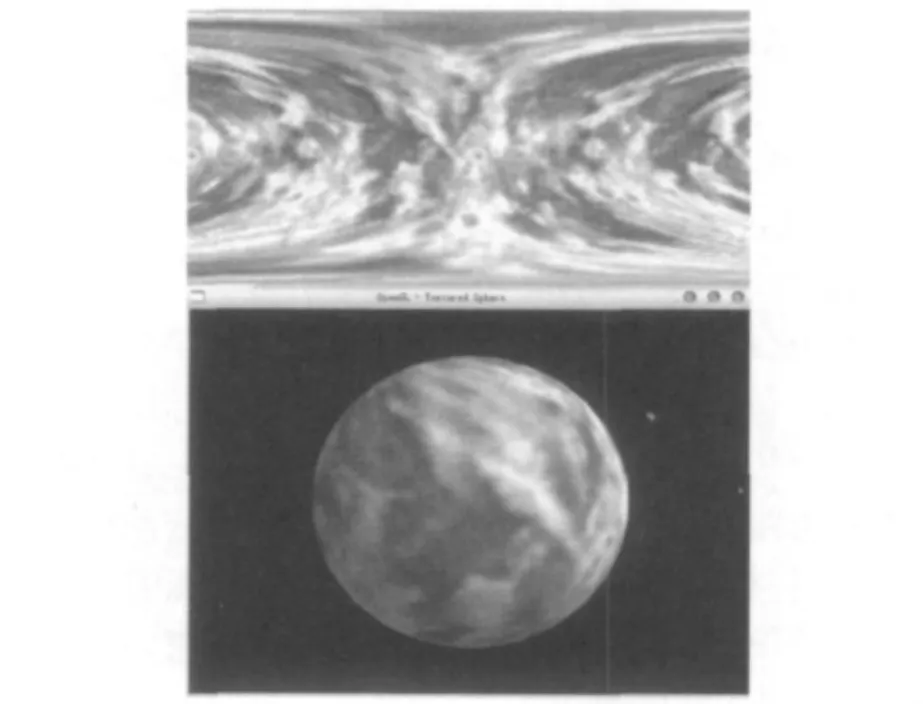
图6 改进后的纹理映射

4 结束语

在原有纹理映射算法的基础上提出了对纹理图案做合理的拉伸变形和对接缝处做三角匹配两点改进，明显改进了传统算法在两极处出现汇聚现象和在接缝出产生的不连续现象，显著提高了纹理映射的质量与真实感。

［1］江巨浪.曲面纹理生成方法及实现的研究［D］.合肥:合肥工业大学，2006.

［2］BOWDEN R，MITCHELL T A，SAHARDI M VISION.Real－time dynamic deformable meshes for volumetric segmentationandvisualisation ［J］.InProc，BMVC，1997，1:310－319.

［3］PIPONI D，BORSHUKOV G.Seamless texture mapping of subdivision surfaces by model pelting and texture blending:computer graphics proceedings［C］.Annual Conference Series(SIGGRAPH2000)，2000:471 －478.

［4］PRAUN E，FINKELSTEIN A，HOPPE H.Lapped textures［C］.Computer Graphics Proceedings，Annual Conference Series(SIGGRAPH2000)，2000:465 －470.

［5］汤颖，孙汉秋，张宏鑫，等.用户控制的纹理合成［J］.计算机辅助设计与图形学学报，2004，16(10):1412－1418.

［6］MALLLOT J，YAHIA H，VERROUST A.Interactive texture mapping［C］.Computer Graphics Proceedings，Annual Conference Series(SIGGRAPH93)，1993:27 －34.