小波算法在光纤测量中的应用

2011-06-01张伟

电子科技 2011年12期

张伟

(同济大学电子与信息工程学院，上海 200092)

在通信技术中，光纤作为传输的媒介，了解其传输衰减特性以及发生故障时对其进行精确有效的定位至关重要。OTDR(光时域反射仪)作为光纤检测中的重要仪器，具有测试时间短、测试速度快、测试精度高等特点，文中将以OTDR的原理与应用着手展开研究与讨论。

1 OTDR工作原理

OTDR利用光纤在传播过程中产生的瑞利散射和菲涅尔反射原理进行故障检测，瑞利散射是由于光信号沿着光纤产生无规律的散射而形成，OTDR测量回到OTDR端口的那部分散射光，这部分散射光的强度随着激光在光纤中传输的距离增加而减小，反射光强度的db值与距离形成一条直线，可以根据这条直线的斜率判断该光纤的衰减特性，直线越平坦表明该光纤的衰减值越小。而产生菲涅尔散射是由于光纤中的个别杂质或光纤的衔接点等原因所致，这些点会产生很强的反射光到OTDR的端口，可利用这些事件点对光纤进行故障定位。

2 小波滤波和定位原理

由于OTDR信号中事件点的幅值变化较剧烈，呈现为瞬间增强和瞬间回弱，若小波函数选择不当，在这些不连续点处容易造成伪吉布斯(Pseudo－Gibbs)现象，经过多种小波的研究和实验后，确定db1小波不会造成伪吉布斯现象，但是随着分解层数的增加，会产生较严重的阶梯型效应，这也是db1小波的一个缺点。为解决这一问题，采用平移不变量(Translation Invariant，TI)小波阈值去噪法［1］，理论和实验证明，该方法不会造成伪吉布斯现象和阶梯型效应。

该算法描述如下:假设输入的含噪信号为Xi，i=0，1，…，n－1，Sh表示对信号X在时域循环平移h的算子，即(ShX)i=X(i+h)modn，得到的平移信号为ShX。然后，用T表示用软阈值法对信号进行去噪处理，则去噪信号表示为T(ShX);对去噪后的信号再进行相反的平移h，可得最终去噪信号S－h(T(Sh(X)))。由于正交小波具有平移不变的特性［2］，因此，上述算法在理论上是可行的。

由于OTDR信号一般存在若干个连续性差的位置，它们之间会相互干扰，也就是说一个不连续点的最佳平移可能是另一个不连续点的最差平移，所以这样的平移并不是一次性的，需要多次平移→去噪→平均运算［3－4］。G.Beylkin最早发现在这种算法中平移所有的小波系数是不必要的，并提出了TI算法的快速实现［5］。

设信号的长度n=2J，原始信号x=βJ，0，G和H分别表示二元抽样的高通滤波器和低通滤波器算子，首先对S0βJ，0与S1βJ，0进行正交小波变换［6］，记为

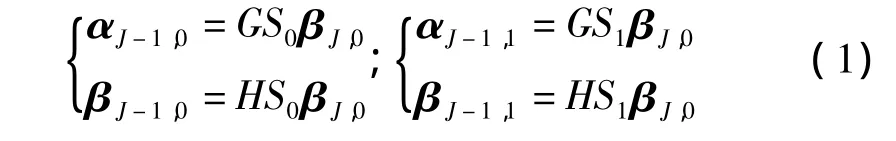
然后，对低频向量 βJ－1，0，βJ－1，1继续进行小波分解，得到高频部分 αJ－2，0，αJ－2，1，αJ－2，2，αJ－2，3和低频部分 βJ－2，0，βJ－2，1，βJ－2，2，βJ－2，3，表达如下:

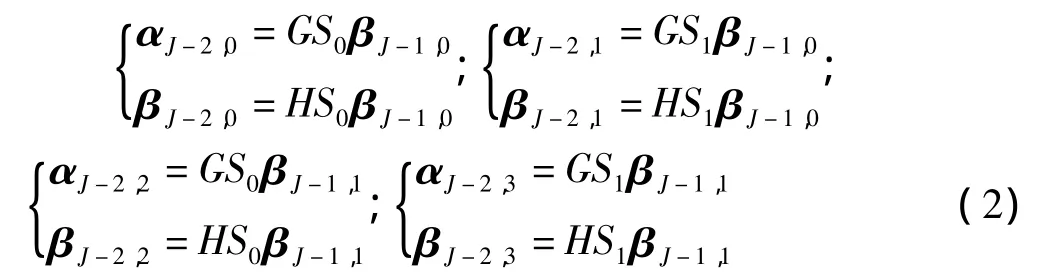
这样一直分解到分解级l=L≤J，而对于 βj+1，k，分解过程表示为:

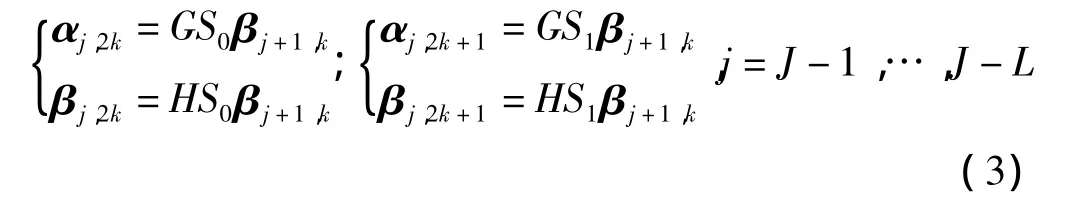
上述变换结果可存放在一个TI表中，其大小为n(L+1)，n表示信号的长度，L表示小波分解的层数。利用软阈值法对高频系数进行处理后，即可进行信号的重构，TI重构算法如下:

设G和H分别表示二元上抽样的高通滤波器和低通滤波器算子［7］，从j=J－L开始，对每个k，0≤k＜2j，计算式(4)

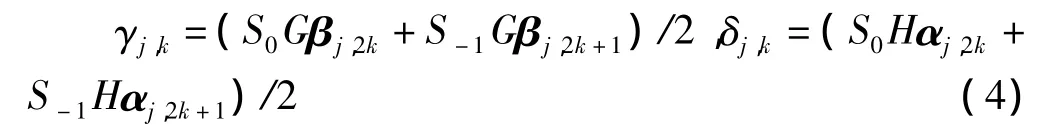
得到 βj+1，k= γj，k+ δj，k，当对分辨率j对应的所有k计算结束后，将j=j+1，重复计算该过程指导j=J。计算的最后结果将得到βj，0，即用平移不变量小波阈值去噪法的最后结果信号。

实验表明这种算法具有较好的滤波效果，但其代价是每一级小波运算的数据量相同，比普通的小波算法运算量高，该算法的计算复杂度为O(nLog2n)。

3 算法仿真与实现

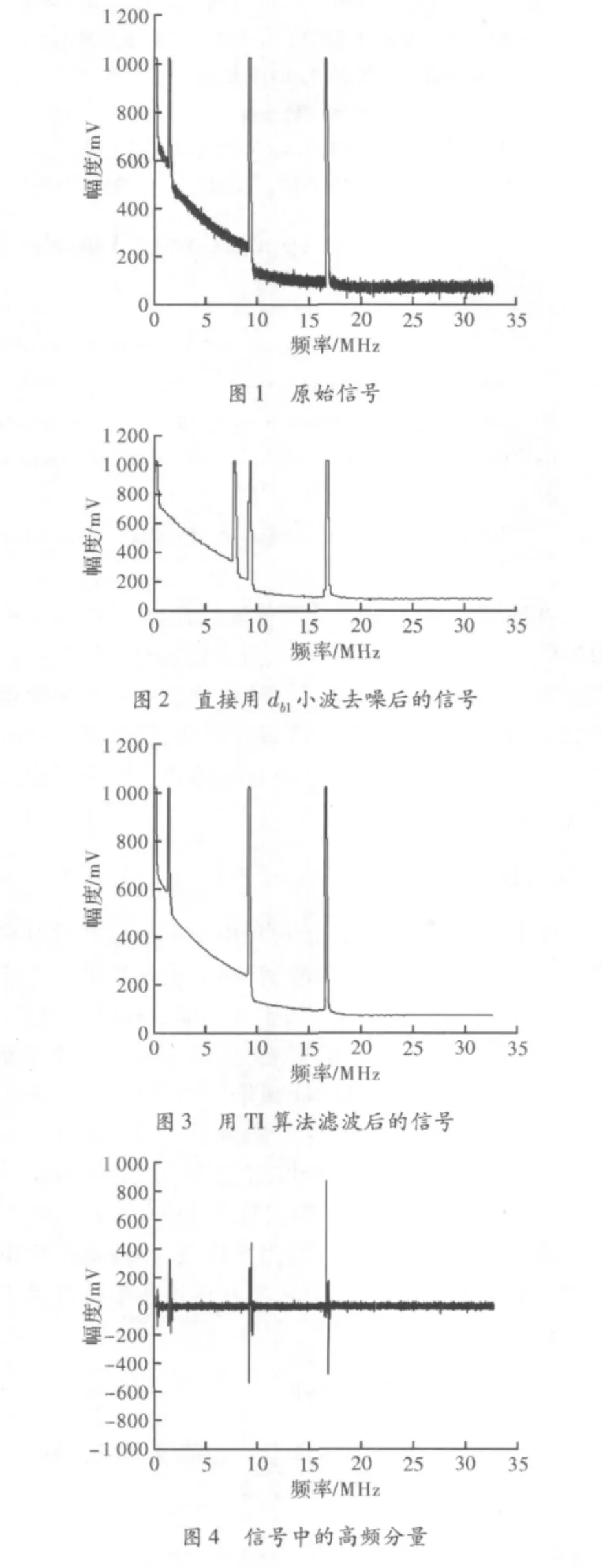
图1是用OTDR通过ADC采样得到的原始图像，可以看出图像受到较为严重的噪声干扰，这样的信号在计算信号衰减值时候会有较大困难，图2是直接用db1小波进行7层去噪后重构得到的信号，从图中可以看出有明显的阶梯型效应，原因是因为db1小波是不连续的小波。而图3是用平移不变量小波阈值去噪法得到的滤波后的图像，其中使用的阈值为软阈值，从图像上可以看出滤波后的图像无伪吉布斯现象和阶梯型效应。图4是将原始信号进行7级小波分解，然后对高频分量进行重构后的图像，从图像中可以看出，信号的事件点在高频分量中表现突出，利用高频分量可进行事件点定位。

实验结果表明，利用平移不变量小波阈值去噪法可以有效地去除伪吉布斯现象和阶梯型效应，其效率也可以被大多数处理器接受。笔者已将该算法在实际项目中应用，使用的处理器为ARM9，实践证明该算法具有较好的实用性。