利用Duffing方程组检测随机相位的正弦信号

刘 立

(华北电力大学电子与通信工程系，河北保定 071003)

文中采用的Holmes型Duffing方程的一般形式如式(1)所示

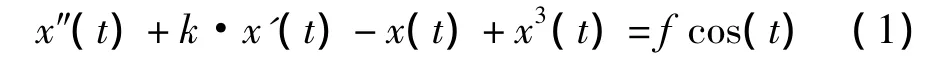
fcos(t)为周期策动力，k为阻尼比，－x(t)+x3(t)为非线性恢复力。若k固定，则f超过一定阈值fc后继续增大，系统很快出现周期倍化分叉，随后进入混沌状态;随着f继续增大，当f大于另一个阈值fd时，系统进入大尺度的周期运动状态［1－2］。

文献［3］分析了如果要使系统运行轨迹发生改变，被测正弦信号的相位必须在一定范围内取值，而且相差过大时系统很容易收到噪声影响。而在实际的通信系统中，接受信号acos(ωt+θ)的相位不可能总是为0或接近0，而是随机分布的，因此本节讨论一种利用Duffing方程组检测随机相位的微弱信号的实现方法［4］。

1 原理分析

将2π均匀N等分，令N个Duffing方程的周期策动力分别预置这N个初相位［4］，即 Φi=(2πi/N)，i=0，1，2，…，N－1。

得到如下N个方程构成的方程组

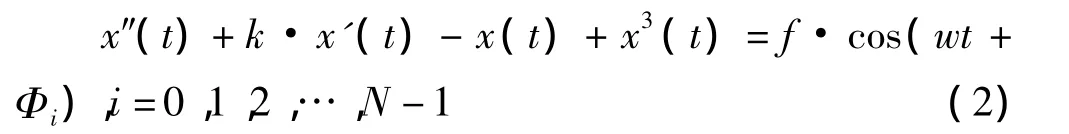
仿照文献［5］中求混沌阈值的方法，容易推出无论Φi取何值，上述方程都存在混沌解，而且混沌阈值的表达式为［5］

当k(k=0.5)固定时，各方程的阈值fd近似相等，但也有所不同。因此预先找出各fdi，并将各方程的策动力f预设在fdi，此时各个方程的解皆处于混沌状态。

按照文献［3］中的参数设置，通过实验分别找出了16个阈值，如表1所示。

表1 策动力的相位φi与阈值fdi对应表

虽然已求出16个方程对应的阈值，但并不是16个方程同时用于检测信号。当待检测信号加入系统时，只有一个方程起作用，可以逐个验证每个方程，看是否有能够将信号检测出来的方程出现，将所有能检测信号的方程都作为有效，将检测到的信号求平均值。

待检测信号的未知相位θ可能会出现两种情况:

(1)待检测信号的相位θ与16个策动力的初相位θi，i=0，1，2，…，15 之一相等。则当待测信号通过系统时，该θi对应的方程出现由混沌状态进入大尺度周期状态解的情况，可以准确地检测出待检测信号幅值。

(2)待测信号的相位θ处于两个θi之间。通过仿真实验发现，当待测微弱信号通过系统时，方程组中可能会有两个甚至多个出现临界状态的转变方程。为减小检测带来的误差，通过求平均的方法来减小误差。

2 仿真结果

上节求出16个方程对应的阈值，本节将用来检测信号。实验时选取k=0.5，ω=100π rad/s。

实验1 加入信号s=0.002 4cos(100πt+π)。

首先调整系统方程策动力的相位，使θ=θ0=0，然后调整幅值f0，使得f0=fd0=0.825 9，此时系统处于临界状态，然后将信号s加入系统，此时发现系统回到混沌状态，这说明待测信号的相位不在0附近。

然后继续改变系统策动力的幅值与相位，使θ=θ1=0.125π，f1=fd1=0.825 9，此时系统又处于临界状态，然后继续将信号s加入系统，此时发现系统又回到混沌状态，说明待测信号的相位同样不在0.125π附近，然后继续将幅值与相位改变。

实验发现，当θ=θ8=π，f8=fd8=0.825 8时系统出现大尺度周期运动状态，利用信号检测方法调整f8，实验发现当f8=0.823 5时，系统重新回到临界状态。因此待测信号的幅值a=fd8－f8=0.825 8－0.823 5=0.002 3。误差为0.002 4－0.002 3=0.000 1。

实验继续下去，发现没有出现大尺度周期运动状态的方程，因此最终检测的信号幅度为0.002 3，相位为π。

实验2 加入信号s=0.002 4cos(100πt+15π/16)。

仿照实验一的步骤，当θ=θ7=0.875π，f7=fd7=0.826 0时系统出现大尺度周期运动状态，调整f7，实验发现当f7=0.824 4时，系统重新回到临界状态。因此待测信号的幅值a1=fd7－f7=0.826 0－0.824 4=0.001 6。误差为0.002 4－0.001 6=0.000 8。

实验继续，当 θ=θ8=π，f8=fd8=0.825 8时系统出现大尺度周期运动状态，调整f8，实验发现当f8=0.824 3时，系统重新回到临界状态。因此待测信号的幅值a2=fd8－f8=0.825 8－0.824 3=0.001 5。误差为0.002 4－0.001 5=0.000 9。

实验继续下去，发现没有出现大尺度周期运动状态的方程。为了提高检测精度，采用时域经常用到的平均求值方法。将检测到的a1，a2求平均，可以得到

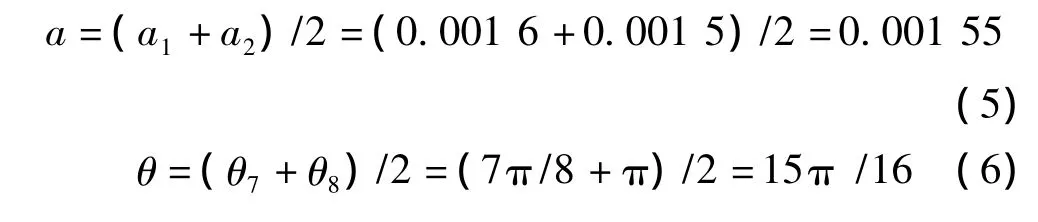
3 结束语

对于相位未知的微弱正弦信号，可以采用16个方程的方法将带有未知相位微弱正弦信号检测出来，利用这种方法可以检测到的相位误差＜π/16。上述仿真实验是在没有噪声输入时进行的，幅值误差主要为系统误差和相位差引起的误差。如果实际系统中有噪声存在，那么测量误差会增加，但是只要能检测出任意相位的输入信号，这种检测方法则是有效的。

［1］王冠宇.混沌振子在强噪声背景信号检测中的应用［J］.仪器仪表学报，1997，18(2):209 －212.

［2］聂春燕.基于混沌相平面变化的弱信号检测方法研究［J］.长春大学学报，1999，9(4):1 －4.

［3］刘立，孙军.基于混沌振子的微弱信号检测方法研究［J］.沈阳农业大学学报，2005，36(6):667 －670.

［4］李健，何坤，乔强，等.应用混沌系统实现弱信号的检测［J］.四 川 大 学 学 报:自 然 科 学 版，2004，41(6):1180－1183.

［5］李月，杨宝俊.混沌振子检测引论［M］.北京:电子工业出版社，2004.