具有隐私保护的外包数据库合计查询方案

蒋亚军 ，杨 波，张明武，陈旭日

(1. 华南农业大学 信息学院，广东 广州，510642；2. 湖南科技学院 计算机与通信工程系，湖南 永州，425100；3. 上海大学 计算机工程与科学学院，上海，200072)

随着计算机网络技术的迅速发展，数据库外包已成为一个重要的发展趋势。数据所有者将数据管理业务委托给第三方服务提供者，服务提供者提供软硬件和网络资源，为数据所有者及用户提供远程的数据库创建、存储、更新和查询等数据管理服务，从而优化数据所有者的资源配置，降低软硬件投资成本，减轻管理和维护任务[1-2]。然而，由于第三方服务提供者并非完全可信，因此，数据的隐私性和安全性已成为数据库外包系统中一个重点关注的问题。大型数据库中合计查询是一项非常频繁和重要的操作，而外包数据库系统中的合计查询除了要求得到正确的查询结果外，还要保护查询过程中数据的隐私和安全。近年来，许多外包数据库查询方法利用数据加密隐藏外包数据[3-7]，然而，数据加解密的计算复杂性增加了计算和通信代价，因而效率不高。而通过秘密共享实现数据库外包，并对外包数据进行隐私保护计算[2,8-10]，避免了数据加解密，极大地提高了计算效率，目前已成为外包数据库查询方法研究中的热点。在此，本文作者提出一种基于秘密共享的合计查询方案，利用Mignotte秘密共享方案将数据库外包给服务提供者，服务提供者根据用户提出的合计查询要求，在不泄露外包数据的前提下协同计算查询结果并将之响应给用户，用户在信赖数据所有者的前提下，根据数据所有者对数据项的承诺和生成的 Merkle哈希树对查询结果进行验证。

1 基础知识

1.1 Mignotte秘密共享方案

Mignotte秘密共享方案[11-12]是通过中国剩余定理将秘密x让m个用户共享，由其中任意k个用户能够恢复秘密x，但少于k个用户不能恢复秘密x。

设m为大于2的正整数，2≤k≤m，选择m个两两互质的正整数 d1, d2, …, dm(d1＜d2＜…＜dm)，令，要求 β ＜x＜α。方案描述如下：

1.2 Pedersen承诺方案

Pedersen承诺方案[13]包括承诺者和验证者两方，双方商定 g ∈ Gq， h ∈ Gq，且 lo ggh 未知。承诺者随机选择随机数 r ∈ Zq，其对 x ∈ Zq的承诺为 Cr(x)=gxhr∈ G 。验证者不能从Cr中得到任何x的消息，而承诺者不能谎称Cr为x′的承诺，这里 x ≠ x'。

1.3 Merkle哈希树

Merkle哈希树[14]是一个二叉树，给定向量=(,… ,xn)，F(·)为公开的单向哈希函数，定义结点函数H(i,j,)如下：

2 本文方案

在外包数据库模型中有3个实体：数据所有者、服务提供者和用户，这些实体的角色如下所述。

(1) 数据所有者创建和维护数据库，对数据项进行承诺，产生和维护Merkle哈希树，并将数据库外包给服务提供者；数据所有者的符号为DO。

(2) 服务提供者负责外包数据库的存储和管理，响应用户查询；本文方案中假设有m个服务提供者，符号为SP1, SP2, …, SPm。

(3) 用户通过服务提供者进行查询，并通过数据所有者对数据项的承诺和产生的 Merkle哈希树验证查询结果的正确性；用户的符号为U。

数据所有者、服务提供者和用户三者的关系如图1所示。

图1 外包数据库模型Fig.1 Outsourced database model

为简化描述，假设数据库D为n行1列，且每个数据项为正整数，设D=(x1, …, xn)(其中，β＜xi＜α，1≤i≤n)，且 。方案分为承诺、分配、查询、响应和验证5个阶段。下面以用户提出的求和查询为例进行阐述。

2.1 承诺阶段

在承诺阶段，数据所有者完成对数据的承诺，并根据承诺产生Merkle哈希树。设数据所有者选择公共参数g和h， g ∈ Gq， h ∈ Gq，然后对各数据项承诺：c1= Cr1(x1)， c2= Cr2(x2)，…， cn= Crn(xn)。令向量=(c1, c2, …, cn)，数据所有者根据向量产生Merkle哈希树。设数据所有者的公开钥和秘密钥分别为pk和sk，则数据所有者利用自己的秘密钥sk对根结点签名为sigsk(H (1 ,n,，并将和sigsk(H ( 1,n,广播给所有服务提供者。

2.2 分配阶段

在分配阶段，数据所有者将数据库外包给m个服务提供者。对于每个数据项xi和相应的随机数ri，服务提供者SPj的共享为yij和zij。其中：

2.3 查询阶段

在查询阶段，用户向服务提供者发出查询请求。设用户向服务提供者SP1提出求和的请求S⊆{1 ,2,…,n}，SP1则向其余任意的k-1个服务提供者发出合作求和的请求。

2.4 响应阶段

在响应阶段，k个服务提供者在保证各自共享隐私的前提下协同计算查询结果，并将之响应给用户。设Ω是k个服务提供者的联盟(包括SP1)，它们共同计算XS。其中任意服务提供者SPj中，j∈Ω，Ω⊆{1,2,…,m}。

(1) Ω中每一个服务提供者SPj计算：

然后，SPj将传送至SP1。

(2) SP1收集其他k-1个后，计算：

(3) 服务提供者 SP1将 XS，RS，C和sigsk(H ( 1,n传送至用户。

2.5 验证阶段

在验证阶段，用户在不知道数据库D的数据项和服务提供者获得的共享的前提下验证XS。

3 方案分析

3.1 正确性分析

因此，XS可通过求Ω中每个服务提供者的而获得，即响应阶段中的求和 XS是正确的。显然，相对应的平均值为： ||/SXS(其中 ||S为集合S中元素个数)。

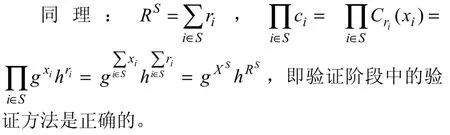
3.2 隐私性和安全性分析

定理1 半诚实的服务提供者的共享对于其他服务提供者具有隐私保护。

证明 在SP1与其他k-1个服务提供者协同计算求和时，是通过求Ω中每个服务提供者的而获得，而，因此，SP1无法从中分离出uij，其他k-1个服务提供者的共享具有隐私性。

定理2 本文方案面对k-1个恶意服务提供者共谋时，数据在计算上是安全的。

证明 当k-1个服务提供者勾结时，这k-1个服务者设为 S Pj1,SPj2,… ,S Pjk-1。如果它们想用其共享恢复 xi时，根据Mignotte秘密共享方案，可以求得1个唯 一 值(dj1dj2… djk-1)， 并 且 xi=xi'm oddj1dj2…djk-1，这意味着在[β,α]上至少有c=个值有可能是x(其中，“[ ]”表示取整)。假i如c足够大(例如c=106)，则 xi在计算上是安全的，即保证了数据的隐私性。

定理 3 恶意的服务提供者在多项式时间里不能生成一个有效的查询结果。

证明 恶意服务提供者要想在多项式时间里生成一个有效的查询结果，必须满足如下情形之一：

(3) 仿造数据所有者对一个新的Merkle哈希树进行签名。

对于情形(1)，由Pedersen承诺方案在计算上是不可实现的；对于情形(2)，由于)(·F为单向哈希函数，是无冲突的，因此，在计算上也是不可实现的；对于情形(3)，由公钥加密机制原理要仿造数字签名在计算上也是不可实现的。这个定理保证了数据的完整性。

3.3 效率分析

采用本文方案所得计算复杂度与文献[10]中各参与方的计算复杂度比较结果如表1所示，其中：本文方案中数据库所有者的计算复杂度为o(nm)，文献[10]中数据库所有者的计算复杂度为o(nmk)；本文方案的服务提供者SP1的计算复杂度为o(k)，文献[10]中服务提供者SP1的计算复杂度为o(k2)。显然，由于本文方案使用Mignotte秘密共享方案外包数据库并计算查询结果，与文献[10]中利用Shamir秘密共享方案相比，在数据库外包和查询计算等方面具有更高的效率。

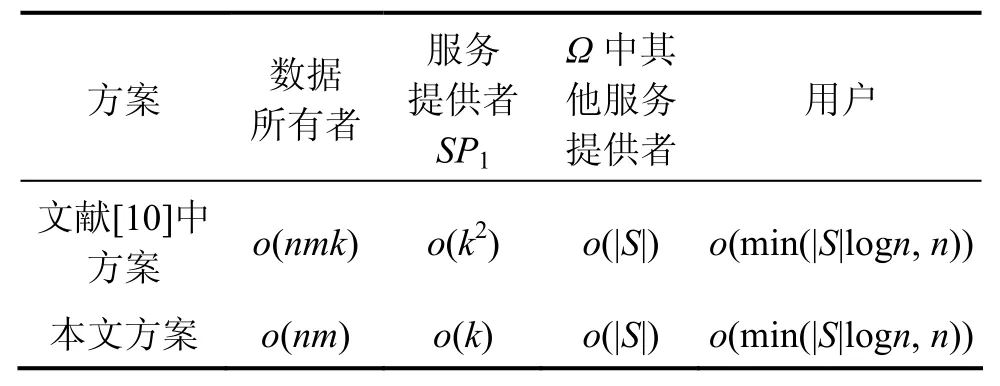
表1 本文方案与文献[10]中各参与方的计算复杂度Table1 Computational complexity of all involved parties in this paper and Ref.[10]

4 结论

(1) 提出了一种具有隐私保护的外包数据库合计查询方案。该方案利用Mignotte秘密共享方案进行数据外包，服务提供者在不能获得彼此外包数据的前提下协同计算查询结果并将之响应给用户。用户可以根据数据所有者对数据项的 Pedersen承诺和生成的Merkle哈希树对结果进行验证。

(2) 所提出的方案可以保护数据项和中间结果的隐私性和安全性，在数据库外包和查询计算等方面具有更高的效率。

(3) 在外包数据库查询方案中，结果验证是重要的组成部分，结果验证效率直接影响着整个方案的效率。将来的工作是对查询结果验证方法进行改进，以降低计算复杂度，进一步提高查询方案的效率。

[1] Hacigümüs H, Mehrotra S, Iyer B. Providing database as a service[C]//Proceedings of the 18th International Conference on Data Engineering. San Jose, USA, 2002: 29-40.

[2] Agrawal D, Abbadi A E, Emekci F, et al. Database management as a service: Challenges and opportunities[C]//Proceedings of the 2009 IEEE International Conference on Data Engineering.Washington DC, USA, 2009: 1709-1716.

[3] Ge T, Zdonik Z. Answering aggregation queries in a secure system model[C]//Proceedings of the 33rd International Conference on Very Large Data Bases. Vienna, Austria, 2007:519-530.

[4] Hacigümüs H, Iyer B, Li C, et al. Executing SQL over encrypted data in the database-service-provider model[C]//Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data. Madison. Wisconsin, USA, 2002:216-227.

[5] Agrawal R, Kiernan J, Srikant R. Order preserving encryption for numeric data[C]//Proceedings of the International Conference on Management of Data. Paris, France, 2004: 563-574.

[6] Mykletun E, Tsudik G. Aggregation queries in the Database-As-a-Service Model[J]. Lecture Notes in Computer Science, 2006, 4127: 89-103.

[7] Yang Z, Zhong S, Wright R. Privacy-preserving queries on encrypted data[C]//Proceedings of the 11th European Symposium on Research in Computer Security. Hamburg,Germany, 2006: 479-495.

[8] Emekci F, Agrawal D, Abbadi A E, et al. Privacy preserving query processing using third parties[C]//Proceedings of the 22nd International Conference on Data Engineering. Washington DC,USA, 2006: 27-36.

[9] Ye Q, Wang H, Tartary C. Privacy-preserving distributed set intersection[C]//Proceedings of the 3rd International Conference on Availability, Security and Reliability. Barcelona, Spain, 2008:1332-1339.

[10] Thompson B, Haber S, Horne W G, et al. Privacy-preserving computation and verification of aggregate queries on outsourced databases[J]. Lecture Notes in Computer Science, 2009, 5672:185-201.

[11] Mignotte M. How to share a secret[J]. Lecture Notes in Computer Science, 1983, 149: 371-375.

[12] Iftene S. General secret sharing based on the Chinese Remainder Theorem with applications in E-Voting[J]. Electronic Notes in Theoretical Computer Science, 2007, 186(14): 67-84.

[13] Pedersen T P. Non-interactive and information-theoretic secure verifiable secret sharing[C]//Proceedings of the 11th Annual International Cryptology Conference on Advances in Cryptology.Berlin: Springer, 1992: 129-140.

[14] Merkle R C. A certified digital signature[J]. Lecture Notes in Computer Science, 1990, 435: 218-238.