一种基于块分类和差值扩展的可逆数据隐藏算法

宋 伟 ，侯建军，李赵红

(1. 北京交通大学 电子信息工程学院，北京，100044；2. 中央民族大学 信息工程学院，北京，100081)

可逆数据隐藏利用可逆变换将数据嵌入宿主图像中，在接收端利用逆变换提取出所嵌入的数据信息并恢复原始图像，最早由Honsinger等[1]于2001年提出，到目前为止大致可分为3类算法：基于差值扩展的算法(Difference expansion, DE)，基于预测误差的算法(Prediction error, PE)和基于直方图平移的算法(Histogram shifted, HS)。差值扩展算法由Tian[2]提出，通过可逆整数变换对像素对差值进行扩展嵌入数据，算法简单，其理论嵌入比特率为0.5 bit/像素。基于该算法，出现了很多新算法[3-7]。Alattar[3]用向量进行差值扩展，如将 3个相邻像素作为1个向量嵌入2 bit信息，理论嵌入比特率为2/3 bit/像素，提高了数据嵌入比特率，但图像质量也随之下降较快。该类算法大多通过行扫描或者列扫描进行嵌入，没有考虑行列之间的区别。Hu等[4]利用整数小波变换，通过阈值选择水平或竖直2个方向进行嵌入。Hsiao等[5]通过方差预测图像块的类型，且进行多方向嵌入，同时采用LSB替代法(Least significant bit substitution method)嵌入辅助信息。Lou等[6]将对数函数引入，提出了一种RDE(Reduced DE)可逆水印算法，减小了数据嵌入对图像造成的失真，但位图信息较大。基于预测误差的数据隐藏算法[8-12]通过预测机制预测目标像素，通过平移误差嵌入数据。常用的预测器有水平预测器、垂直预测器、Causal SVF和 Causal WA 预测器[9]等。Hong等[10]改进了 MED(Median edge detection)，提出了MPE(Modified PE)算法，提高了数据的嵌入容量，然而，其数据嵌入量受到了图像内容的限制，只能在嵌入预测误差为-1和0的目标像素中嵌入数据。Weng等[11]提出了PEA (PE adjustment)预测器将差值扩展和预测误差结合起来，有效地提高了嵌入数据后的图像的质量。基于直方图平移的数据隐藏算法[13-16]通过零点(Zero points)和峰点(Peak point)平移直方图，为数据嵌入提供一定的冗余空间。Lin等[14]将图像的差值直方图代替原始宿主图像的直方图，可产生更多的峰点和零点，并利用多层嵌入策略提高数据嵌入容量。该类方法依赖直方图峰点和零点的数量，数据嵌入容量受到限制。图像由于纹理不同存在平坦和非平坦的区域，平坦区域应该相应地多嵌入数据，而在复杂区域嵌入数据将会造成较大失真；因此，选择一种合适的方式对图像块的类型进行判断，从而嵌入不同量的数据，理论上能够提高嵌入数据后图像的质量。另外，传统的算法对图像进行单向数据嵌入，即逐行进行嵌入或者逐列进行嵌入，没有考虑图像行列间的关系，也影响了图像的质量。为此，本文作者基于图像内容利用图像块嵌入数据前、后均值间的统计特性，设计图像块类型判断准则和数据嵌入方向判断准则，实现了多容量和多方向的嵌入，提高了数据的嵌入容量和嵌入数据后图像的质量。

1 像素对扩展差及向量扩展差

1.1 基于像素对的差值扩展

像素对扩展差的具体过程如下：设原始像素对(u1,u2)为(200, 205)，在数据嵌入过程中，首先计算像素对的均值l和差值d：

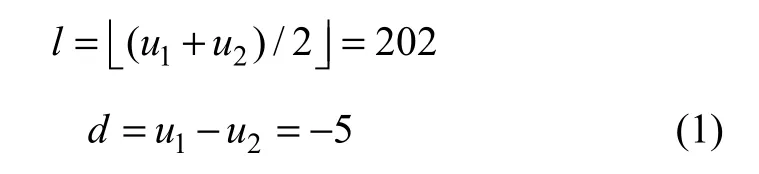
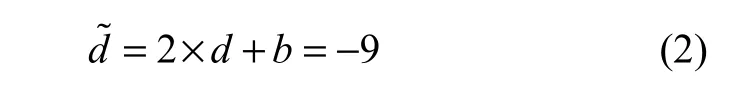
修改后的像素12(,)uu′′为：

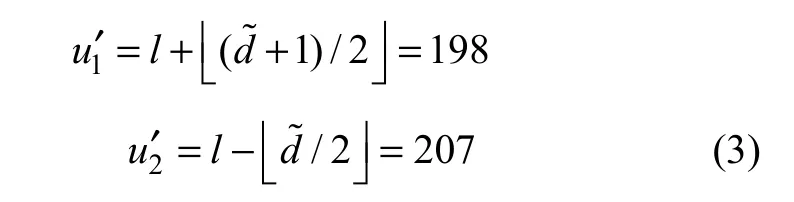
在数据提取过程中，已嵌入数据的像素对12(,)uu′′被选择用来计算均值l和差值d˜：

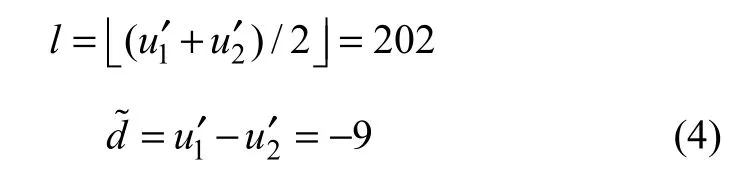
数据b利用最低有效位(LSB)进行提取：

通过如下方程计算得到原始差值d：

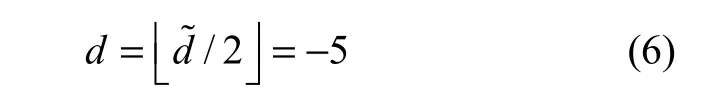
同时，恢复原始像素12(, )uu ：

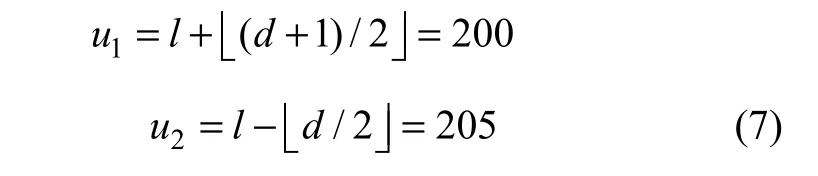
1.2 基于向量的2 bit差值扩展

假设原始像素(u1, u2, u3)为(202, 200, 205)，数据嵌入时，均值d1以及差值d2和d3经计算得到：

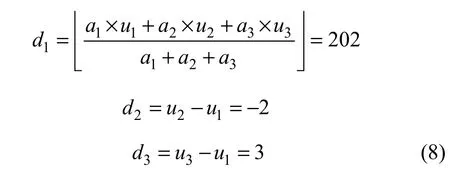
其中：a1, a2和a3为权重，这里赋值为1。设嵌入数据为b1b2=10，则通过如下方式嵌入：

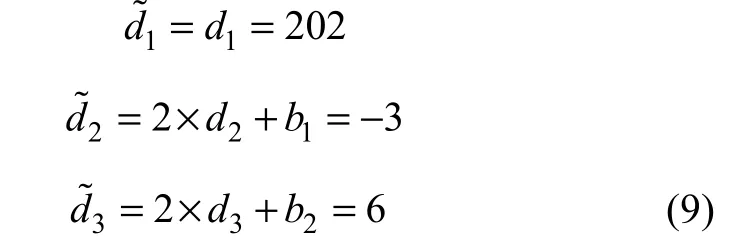
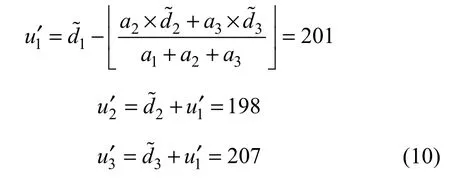
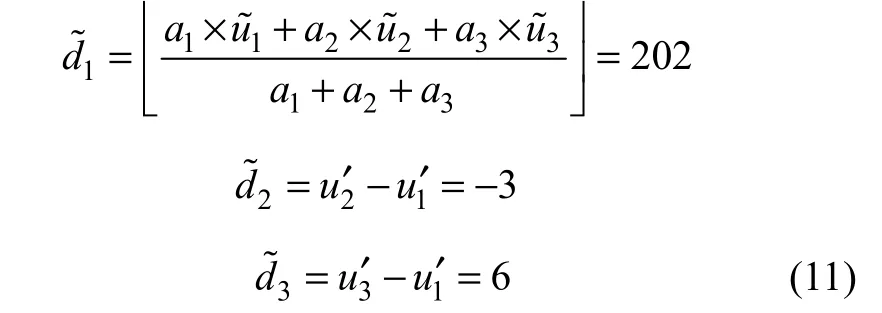
则嵌入的数据b1和b2提取方式为：

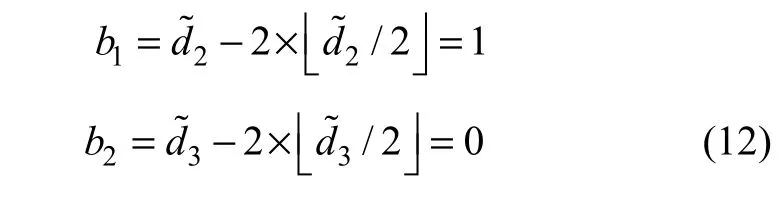
原始均值d1以及差值d2和d3通过如下恢复：

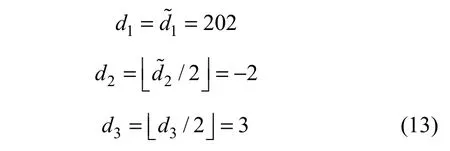
则原始的像素(u1, u2, u3)为：

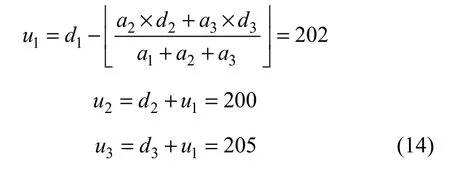
1.3 基于向量的4 bit差值扩展

假设原始像素(u1, u2, u3)为(202, 200, 205)数据嵌入时，差值d2和d3以及均值d1为：

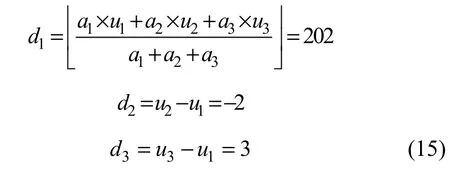
假设嵌入数据为b1b2b3b4=1 101，则通过如下差值扩展嵌入数据：

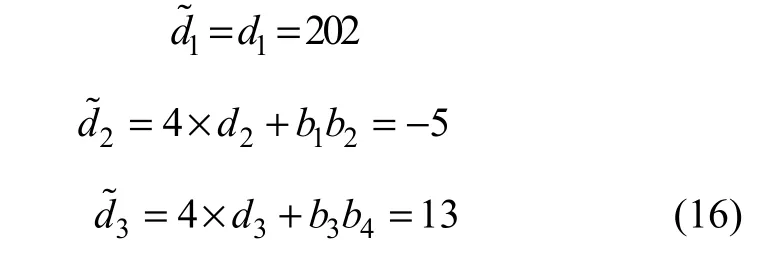
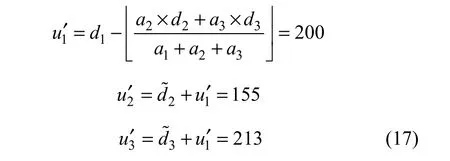
提取过程中，计算均值1d˜以及差值2d˜和3d˜：

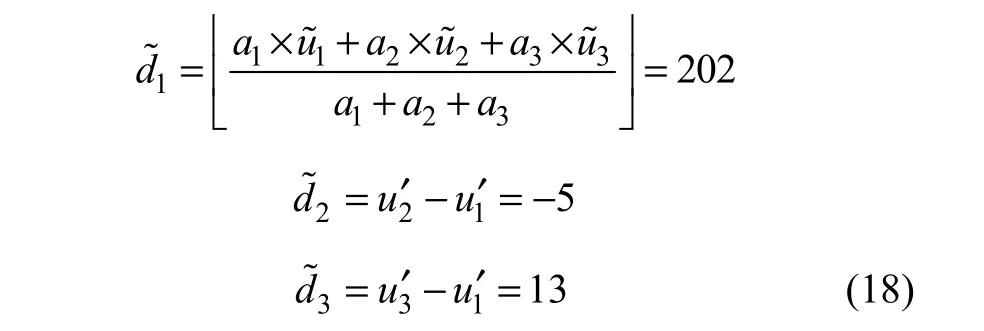
则提取所嵌入的数据b1b2和b3b4为：

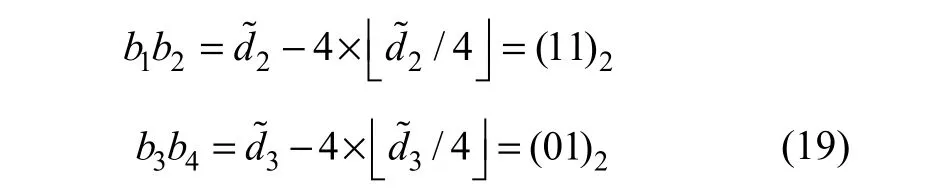
均值d1以及和差值d2和d3经计算得到：

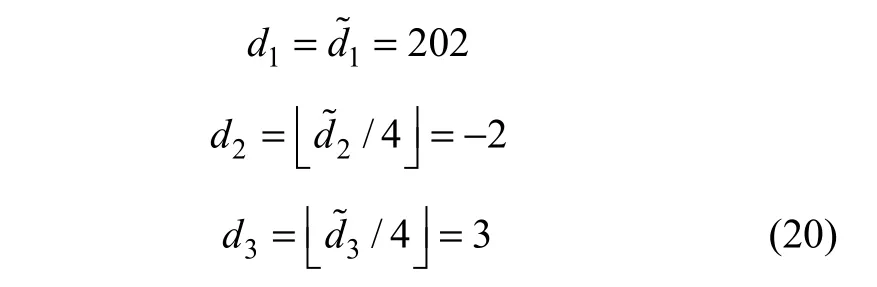
则原始的像素(u1, u2, u3)为：

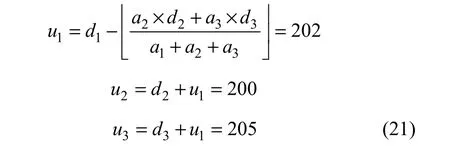
2 图像块分类的差值扩展算法

2.1 数据嵌入算法

数据嵌入过程如图1所示。该算法为基于向量的差值扩展嵌入算法，包括图像区域划分，数据嵌入过程和辅助信息嵌入过程，图像块类型判定准则和图像块嵌入方向判定准则。具体过程如下。

步骤 1 将图像分为数据嵌入区域和辅助信息嵌入区域；

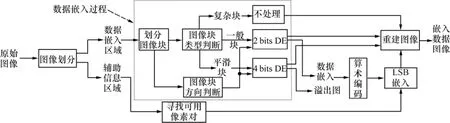
图1 数据嵌入过程图Fig.1 Data embedding procedure

步骤 2 在数据嵌入区域，利用判断准则判断目标图像块的类型和目标图像块的嵌入方向。

步骤 3 对不同目标图像块按嵌入方向嵌入不同比特的数据。若嵌入数据后的像素发生溢出，则不嵌入数据，同时记录位图信息。

步骤4 对位置信息图和2个阈值利用算术编码进行压缩。

步骤5 利用MPE将压缩后位图信息的长度，数据嵌入辅助信息区域。

步骤 6 发送图像块均值差值信息，得到嵌入数据后的图像。

2.1.1 图像区域划分和数据嵌入方向

图像被划分为2个区域:数据嵌入区域和辅助信息嵌入区域(图 2)。辅助信息嵌入区域上半部分高度为3+mod(m, 3)，下半部高度为 3，左半部分宽度为3+mod(n, 3)和右半部分宽度为3(其中m和n分别为原始图像的高度和宽度)。

传统的数据嵌入过程都是在数据嵌入区域通过扫描的方式进行数据嵌入，如在嵌入阶段通过从上到下、从左到右的方式，则在数据提取过程中，首先计算数据嵌入的长度，然后，按照嵌入过程相反的方向对数据进行提取，即从下到上、从右到左。利用图像块间的均值关系对目标图像块进行预测，数据的嵌入和提取可以采用同样的方向，即不必利用数据的长短计算数据提取时的起始位置，然后，采用和数据嵌入相反的方向提取嵌入的数据。该算法利用光栅扫描的方式在数据嵌入区域按照从左向右、从上至下的方式嵌入和提取(图2)。

2.1.2 均值判断图像块类型的有效性

图3所示为原始宿主图像和由图像块均值构成的图像。由图3可知：视觉上的均值图像的大小比原始宿主图像的小，但较好地保留了原始图像的纹理信息和复杂程度，因此，利用均值预测图像块的纹理情况具有一定的理论基础。

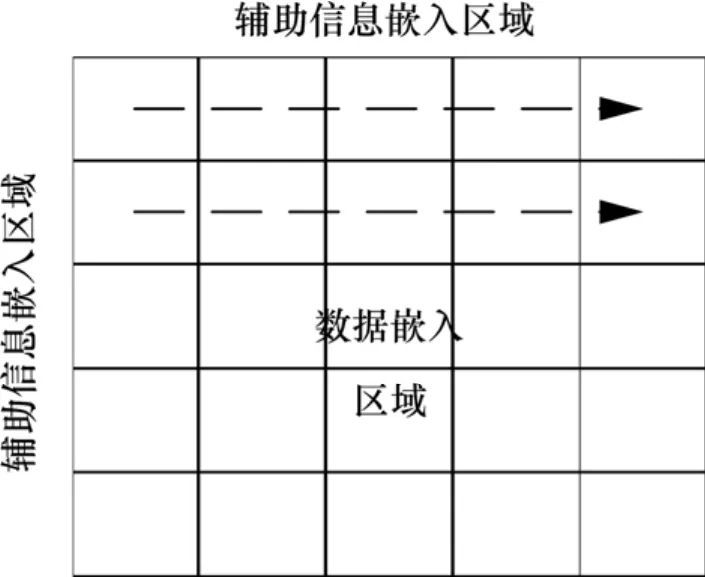
图2 图像划分区域和数据嵌入方向图Fig.2 Image divided area and data embedded direction

图3 均值判断图像块类型的有效性Fig.3 Validity of block’s type decided by mean value

对原始宿主图像(图3(a))进行分块，并计算各图像块的方差和均值。部分相邻图像块的方差和对应图像块的均值如表1所示。方差反映了周围像素值偏离中心像素的程度，方差越大表明纹理越复杂，从而不利于嵌入数据。方差较大的图像块(如方差为6 360的图像块)对应的均值(126)和周围图像块的均值相差也较大而对于方差较小的图像块(如方差为6)，对应图像块和周围图像块的均值差也较小。因此，比较目标像素块和周围图像块均值差值与选取阈值的关系，可以判断不同图像块的纹理复杂程度，从而嵌入不同的数据。

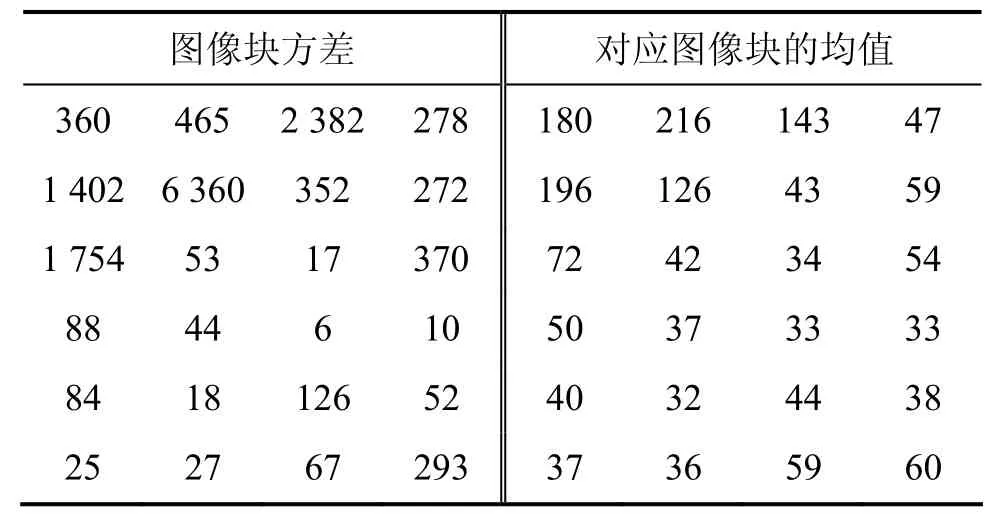
表1 图像块的方差和对应图像块的均值Table1 Variation and mean value of image block

2.1.3 图像块类型判断准则

图像块由于纹理复杂度的不同应嵌入不同的数据。算法将目标图像块(Block0: Target Block)的均值和周围相邻图像块(Block1，Block2，Block3，Block4)(图4)的均值进行比较，将目标图像块分为平滑块(Smooth Block)、一般块(Normal Block)和复杂块(Complex Block)。对于复杂块，数据的嵌入会引起图像的较大失真，因此，不嵌入任何数据。对于一般块，利用1.2节中2 bit差值扩展算法嵌入数据；对于平滑块，利用1.3节中4 bit差值扩展算法嵌入数据。这样，使得增加数据嵌入比特流的同时，尽可能减小数据嵌入对图像带来的失真。具体分析见图5。

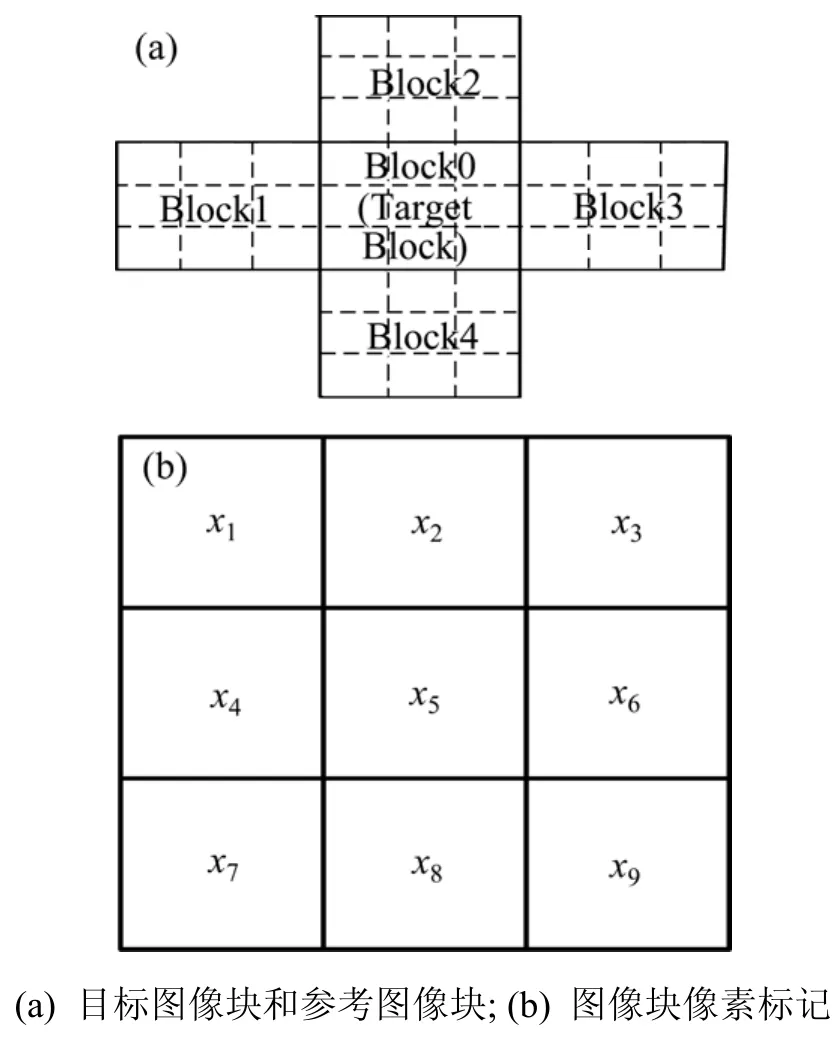
图4 图像块和像素Fig.4 Image blocks and pixels

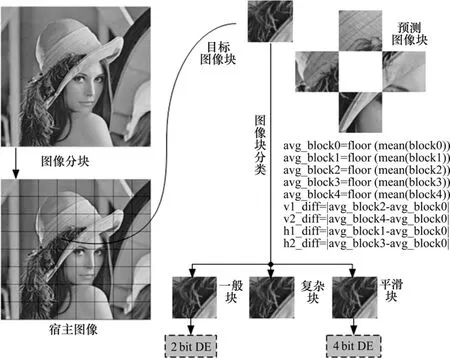
图5 图像块类型判断Fig.5 Classification of image blocks

目标图像块3种类型具体判定准则如下：

2.1.4 图像块嵌入方向判断准则

传统的差值扩展算法进行单一的逐行或逐列嵌入，没有充分利用行列之间的关系。该算法利用像素块间的关系，设计了目标图像块的嵌入方向即水平方向和竖直方向判断准则(图6)。

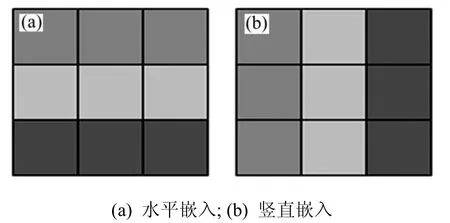
图6 目标图像块嵌入方向Fig.6 Embedding direction of target block

目标图像块嵌入方向具体判定准则如下：

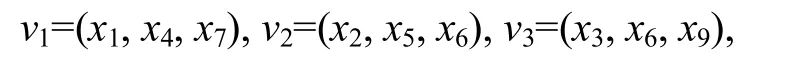
2.1.5 位图信息与阈值处理方式

对于数据嵌入过程中产生的位图和对图像块类型判断所用的阈值，需要在数据提取过程中能够通过数据的提取自动获取，因此，算法采用压缩编码对该部分数据进行压缩，其数据结构构成图如图7所示，压缩后的辅助信息数据结构图如图8所示。在数据提取过程中，辅助信息提取后，按照数据结构图，提取编码后的长度，然后，利用压缩编码结构图提取2个阈值和位置图信息。

图7 压缩编码结构图Fig.7 Structure of compression coding

图8 辅助信息数据结构图Fig.8 Structure of auxiliary information data

2.1.6 辅助信息MPE嵌入方式

对于辅助信息的位置图，大多采用和数据嵌入相同的方式进行嵌入，这样，嵌入的结果是嵌入数据后仍然产生新的位置图，只有通过多次比较和计算才能嵌入辅助信息，使得算法计算量增大，数据处理时间变长。理论上，只要有新的数据需要嵌入，就会产生新的位图信息，因此，需要寻找新的辅助信息嵌入方法。

MPE[10]对MED进行了改进，利用预测误差进行数据的嵌入(式(22))，使得嵌入数据后几乎没有数据溢出，因此，本文选择MPE算法嵌入辅助信息。

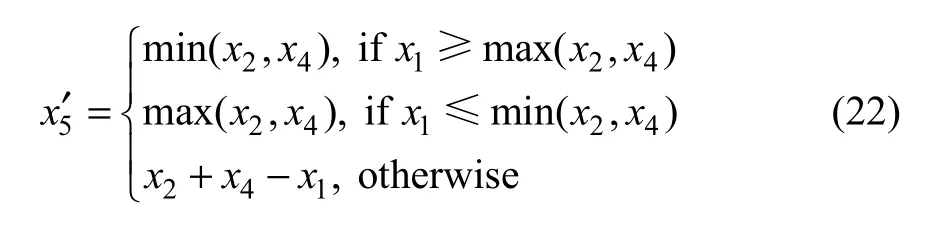
其中：xi为图4中被选取的原始像素；ix′为嵌入位置图信息后的像素。

实验过程中选取大小为 512×512的不同纹理特征的灰度图像作为宿主图像(图 9)，分别为标准图像Lena，Plane，Couple，Milk-drop，Peppers，Baboon，Boats和图像Bridge。

表2所示为8副测试图像(图9)辅助信息区域可用像素的数量和利用 MPE嵌入数据后产生位图信息的情况。由表2可知：可用像素数量大，且嵌入后的位图信息为 0，表明无新位图信息产生，不需采用多次嵌入，多次比较嵌入辅助数据[5]。

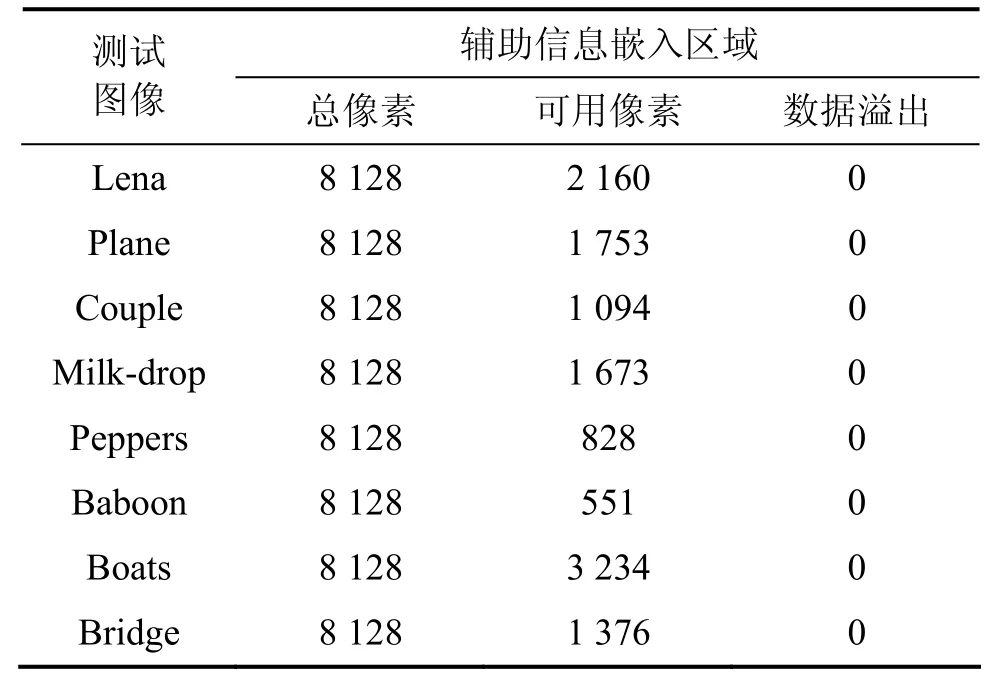
表2 辅助信息区域可用像素及位图信息Table2 Amount of useable pixels and location map

2.2 数据提取算法

数据提取过程与数据嵌入过程相似，具体过程见图10。

步骤 1 将图像分为数据提取区域和辅助信息区域。

步骤2 查找辅助信息区域可用像素，利用MPE提取嵌入数据，并恢复辅助信息区域像素。

步骤3 利用算术编码解码算法对MPE提取出的数据进行解压缩，利用压缩编码结构图分解出阈值和位置信息图。

步骤 4 利用辅助信息和图像块均值差值信息对数据提取区域图像块类型和方向进行判断，提取出目标图像块所含的数据，并恢复原始图像块的像素。

步骤 5 执行上述步骤，直到所有目标图像块检测完成为止，得到嵌入的数据和原始宿主图像。

图9 测试图像Fig.9 Test images

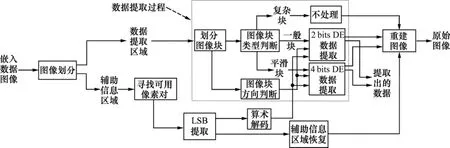
图10 数据提取过程图Fig.10 Data extraction procedure

3 实验结果及分析

3.1 算法性能衡量标准

可逆数据隐藏算法的性能评价标准通常通过数据嵌入比特率和嵌入数据后图像的视觉质量来衡量，将两者有效结合称为综合性能指标。前者通过计算数据嵌入容量和图像大小的比值进行衡量，后者通过峰值信噪比(PSNR，Peak signal-noise ratio)来判定水印的不可见性这一重要特性。

3.2 算法综合性能测试

图11和图12所示为8副测试图像(图9)的综合性能测试结果。从图11可以看出：对于纹理较为简单的图像Plane，由于其像素块间的差值较小，使用较小的阈值就可以将图像块分成不同的类型，同时，在辅助信息嵌入区域，平滑的区域能够产生较多的嵌入信息可用像素，因此，嵌入比特率较高，图像质量较好。对于 Milk-drop图像同样存在这些特性，在该图像的上部分由于存在一定的纹理特征，在嵌入同样比特率条件下，图像的质量较 Plane的低，但当嵌入比特率超过0.5时，图像质量高于Plane图像的质量。这表明该算法充分利用了图像的纹理特征，将图像的内容特性考虑在数据嵌入的过程当中。对于图像Lena，其纹理较Plane和Milk-drop图像的纹理复杂，因此，其综合性能指标图大部分在Plane和Milk-drop的下方。对于图像Couple，其复杂的图像内容使得图像块类型的控制不如前3幅图像容易，嵌入数据后对图像造成的失真较前3幅图像的大，其性能指标与其他图像相比较差。但当图像嵌入容量为 0.7 bit/像素时，图像的PSNR仍然高于30 dB，满足容量和图像质量的要求。

图12所示的4副测试图像的综合性能更进一步地验证了上述的论述。Boats，Peppers，Bridge和Baboon复杂度逐渐增大，同时，Boats的综合性能较好，与其他曲线相比位于图像的上方。其次是 Peppers关系曲线图，位于Boats的下方；最下面的是纹理最为复杂的Baboon图，在嵌入比特率相同时，Boats的PSNR比Baboon的PSNR高达10 dB。这充分表明该算法利用均值控制图像块的类型和方向进行数据的嵌入具有一定的有效性和适用性。

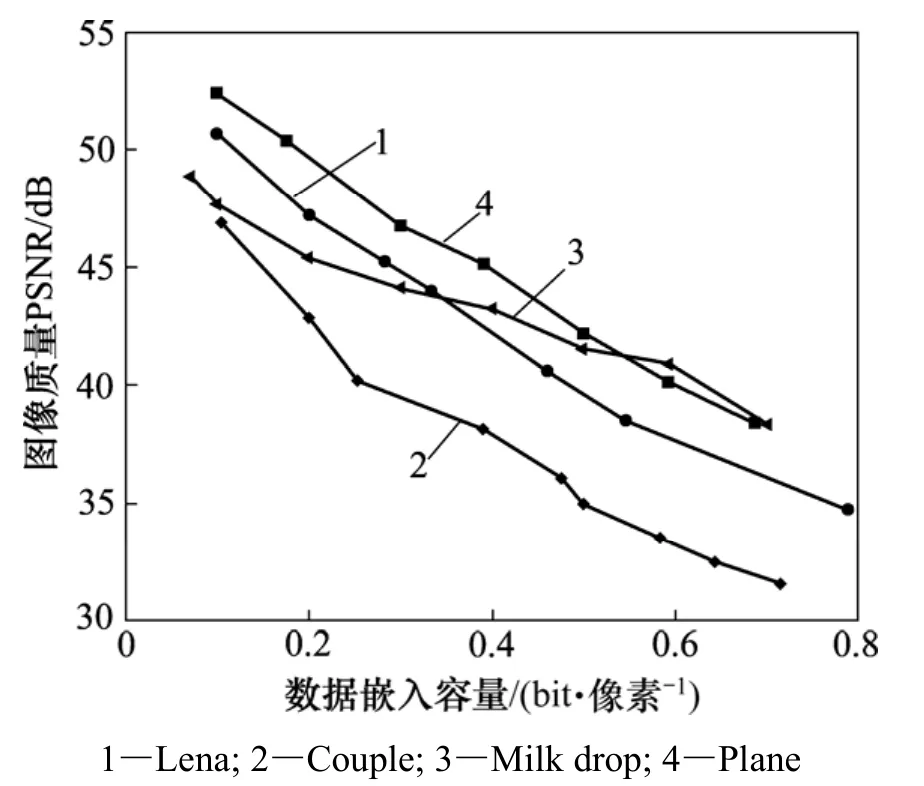
图11 Lena, Couple, Milk drop和Plane的综合性能测试Fig.11 Performance test of Lena, Couple, Milk drop and plane

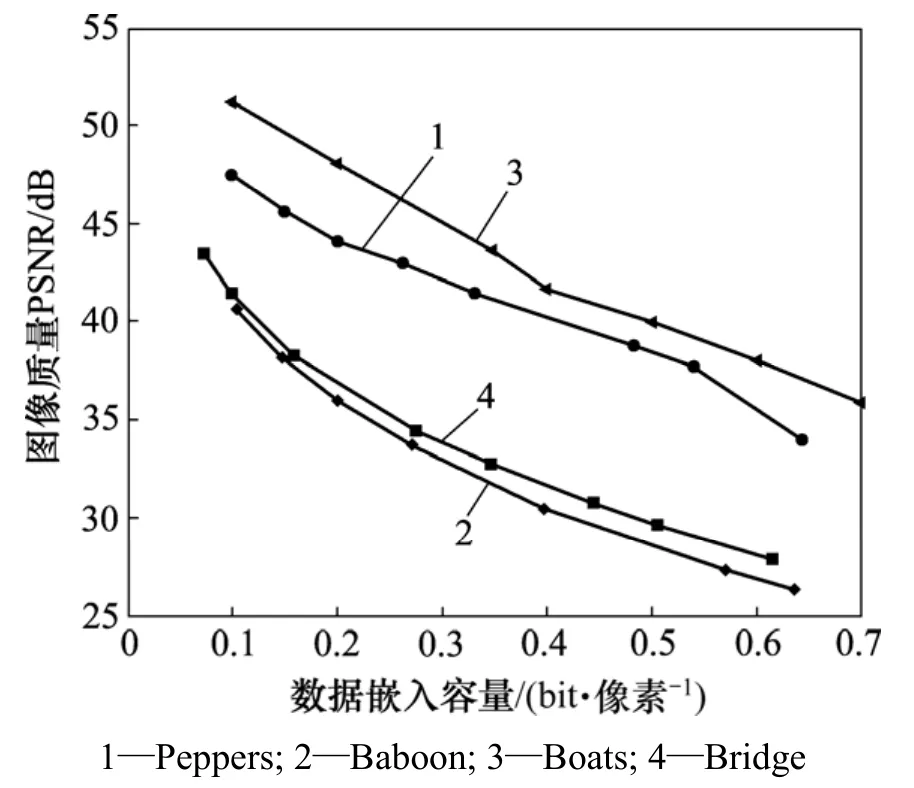
图12 Peppers, Baboon, Boats和Bridge的综合性能测试Fig.12 Performance test of Peppers, Baboon, Boats and Bridge

3.3 算法综合性能对比测试

为了更进一步测试算法的有效性，实验将该算法和优秀的算法Tian的差值扩展算法(DE)[2]与Thodi的预测误差数据嵌入算法(PE)[8]进行对比。图 13～15所示为3种算法在不同纹理图像Baboon，Peppers和图像Lena的综合性能对比关系图。

从图 13可以看出：对于纹理较为复杂的图像Baboon，图像的质量随着嵌入数据量的增多下降较快，在比特率较低时，利用该算法嵌入数据后图像的PSNR比Tian的DE算法嵌入数据后图像的PSNR高达5 dB，比Thodi的PE算法嵌入数据后图像的PSNR高达7 dB，表现出了良好的性能；但随着嵌入数量的增多，复杂的纹理对图像的质量影响越来越严重，但其PSNR仍比DE和PE的高。

对于图像Peppers(图14)，图像良好的局部平滑特性使得不同的图像块根据图像块类型判断准则被很好地区分，从而嵌入数据后对图像造成的失真较小；在不同的嵌入比特率下，该算法的综合性能曲线一直在基于DE和基于PE的综合性能曲线上方，该算法的PSNR比同比特率时DE算法的PSNR高达5 dB，比基于PE的PSNR高达8 dB。可见：该算法对于类似Peppers的局部图像特征较为明显的图像，其综合性能明显高于DE算法和PE算法的综合性能。

图15所示为基于Lena图像的综合性能对比测试曲线图。图像在高嵌入比特率下的质量较高，其PSNR在嵌入比特率高达1 bit/像素时仍高于30 dB；当嵌入数据较少时，该算法的PSNR高于DE和PE的PSNR，当嵌入比特率高于0.6 bit/像素时，Thodi的算法所得的PSNR略高于该算法所得的PSNR。因为高嵌入比特率条件下，位于图像下方较为复杂的纹理图像使得图像块嵌入数据后产生了的较多数据溢出，该部分图像块的不嵌入数据必须通过增大阈值从而增多平滑图的数量进行平衡，从而在一定程度上影响了嵌入数据后图像的质量。但从图15可以看出：该算法的PSNR一直高于Tian的算法的PSNR。因此，该算法对于各种类型的图像都比较适用。

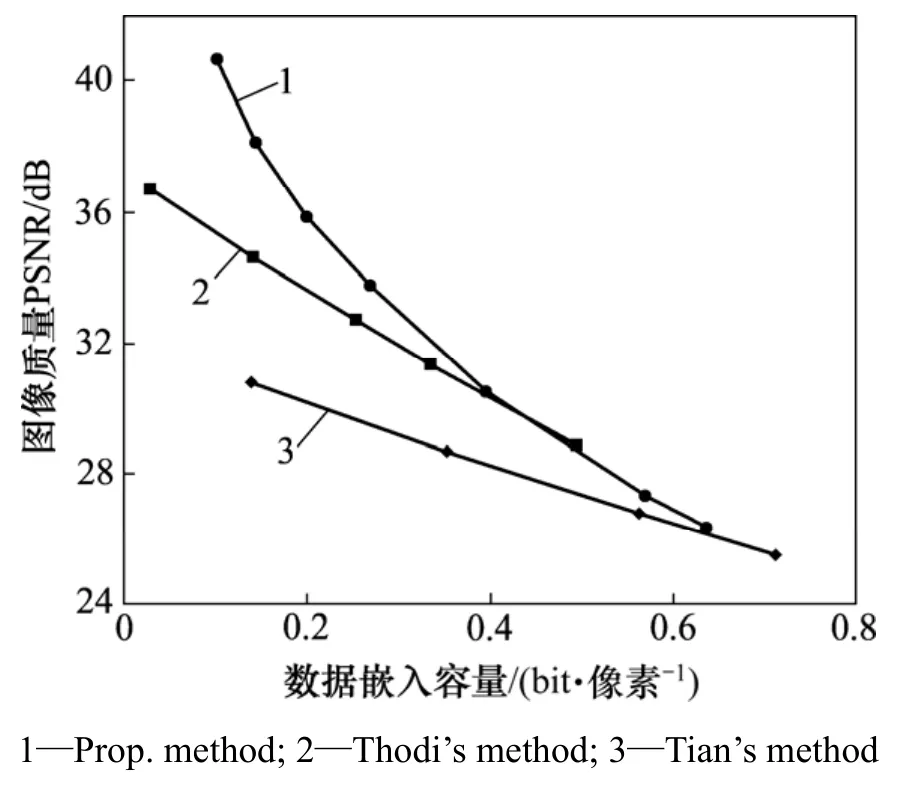
图13 基于Baboon图像的综合性能对比测试Fig.13 Capacity vs. distortion comparison on Baboon

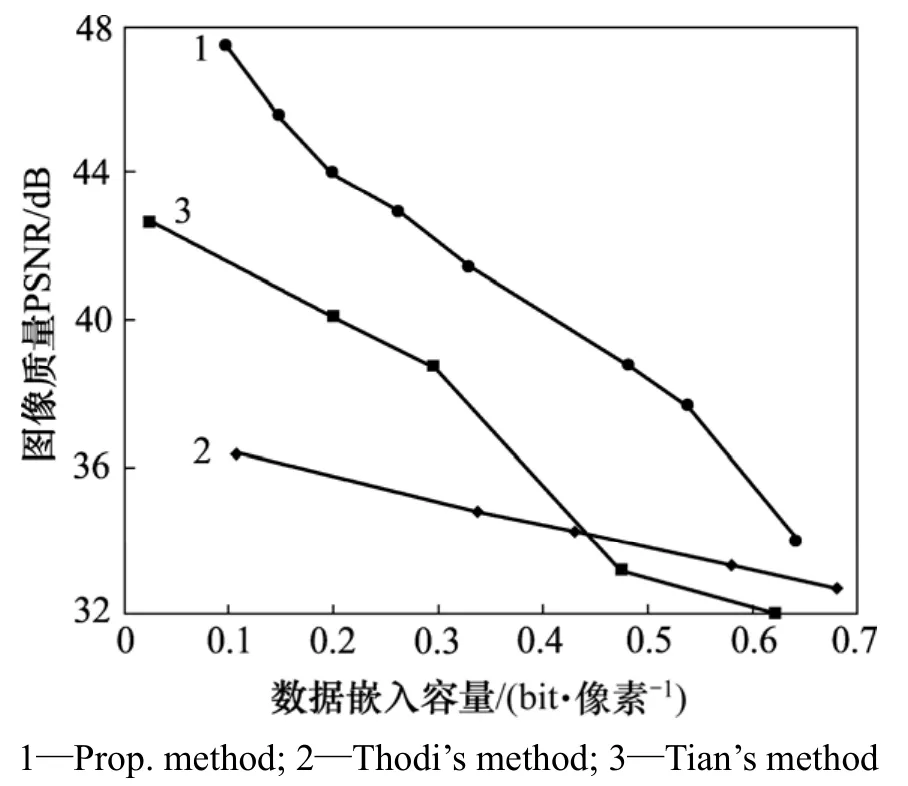
图14 基于Peppers图像的综合性能对比测试Fig.14 Capacity vs. distortion comparison on Peppers

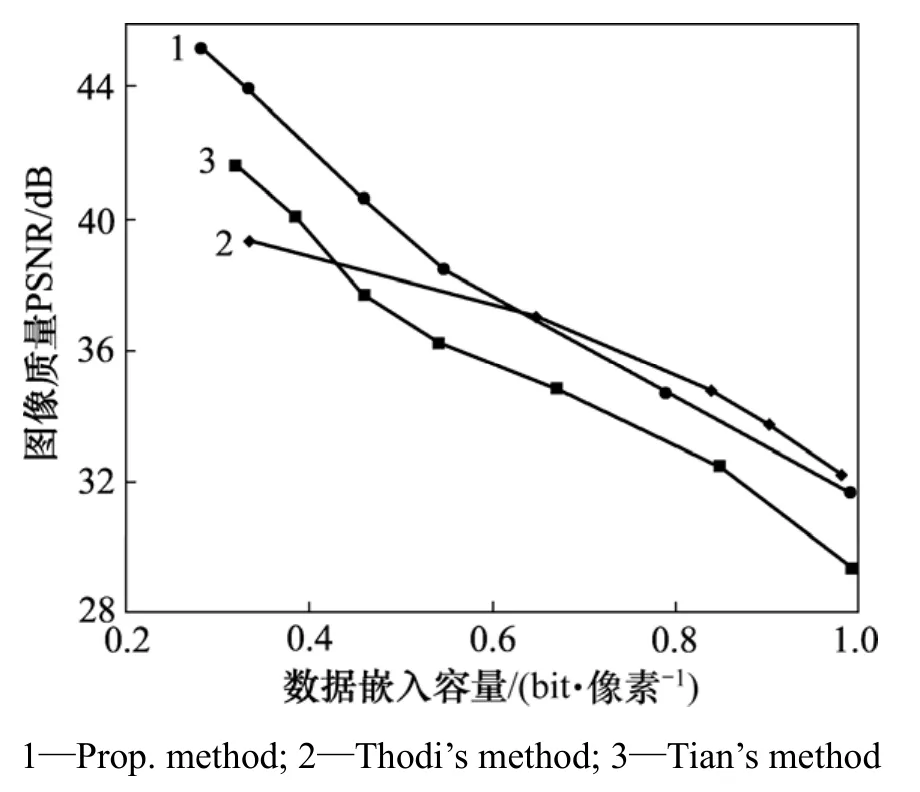
图15 基于Lena图像的综合性能对比测试Fig.15 Capacity vs. distortion comparison on Lena

4 结论

(1) 分析了利用图像块间均值关系判断图像块类型的可行性，设计了图像块类型判断准则；根据不同类型嵌入不同数据量的信息，解决了单一嵌入容量易给载体图像造成较大失真的问题。

(2) 设计了图像块数据嵌入方向判断准则，达到了根据图像纹理信息多方向嵌入数据的目的。

(3) 将差分扩展算法和预测误差算法相结合，有效地提高了图像的可嵌入比特率和嵌入数据后图像的质量。

(4) 下一步研究重点是研究压缩域下的可逆信息隐藏算法和设计，以便有效地减少辅助信息。

[1] Honsinger C W, Jones P, Rabbani M, et al. Lossless recovery of an original image containing embedded data: US 6278791[P].2001-08-21.

[2] TIAN Jun. Reversible data embedding using a difference expansion[J]. IEEE Trans on Circuits and Systems for Video Technology, 2003, 13(8): 890-896.

[3] Alattar A M. Reversible watermark using the difference expansion of a generalized integer transform[J]. IEEE Trans on Image Processing, 2004, 13(8): 1147-1156.

[4] HU Yong-jian, Lee H K, CHEN Kai-ying, et al. Difference expansion based reversible data hiding using two embedding direction[J]. IEEE Trans on Multimedia, 2008, 10(8):1500-1512.

[5] Hsiao J Y, CHAN K F, CHANG J M. Block-based reversible data embedding[J]. Signal Processing, 2009, 89(4): 556-569.

[6] Lou D C, Hu M C, Liu J L. Multiple layer data hiding scheme for medical images[J]. Computer Standards & Interfaces, 2009,31(2): 329-335.

[7] Hu Y J, Lee H K, Li J W. DE-based reversible data hiding with improved overflow location map[J]. IEEE Trans on Circuits and Systems for Video Technology, 2009, 19(2): 250-260.

[8] Thodi M, Rodriguez J J. Prediction error-based reversible watermarking[C]// Proc IEEE ICIP2004. International Conference on Image Processing, Singapore: IEEE, 2004:1549-1552.

[9] Tseng H W, Hsieh C P. Prediction-based reversible data hiding[J].Information Sciences, 2009, 179(14): 2460-2469.

[10] Hong W, Chen T S, Shiu C W. Reversible data hiding for high quality images using modification of prediction errors[J]. The Journal of System and Software, 2009, 82(11): 1833-1842.

[11] WENG Shao-wei, ZHAO Yao, NI Rong-rong, et al. Lossless data hiding based on prediction-error adjustment[J]. Sci China Ser F-Inf Sci, 2009, 52(2): 269-275.

[12] Wu H C, Lee C C, Tsai C S, et al. A high capacity reversible data hiding scheme with edge prediction and difference expansion[J].Journal of Systems and Software, 2009, 82(12): 1966-1973.

[13] Chung K L, HUANG Yong-huai, YANG Wei-ning, et al.Capacity maximization for reversible data hiding based on dynamic programming approach[J]. Applied Mathematics and Computation, 2009, 208(1): 284-292.

[14] LIN Chia-chen, TAI Wei-liang, Chang C C. Multilevel reversible data hiding based on histogram modification of difference images[J]. Pattern Recognition, 2008, 41(12): 3582-359.

[15] Tsai P Y, Hu Y C, Yeh H L. Reversible image hiding scheme using predictive coding and histogram shifting[J]. Signal Processing, 2009, 89(6): 1129-1143.

[16] NI Zhi-cheng, SHI Yun-qing, Ansari N, et al. Reversible data hiding[J]. IEEE Trans on Circuits and Systems for Video Technology, 2006, 16(3): 354-362.