桥台后路堤多级加载下黏弹性饱和成层软土地基一维固结分析

刘萌成 ，朱洪州，彭卫兵

(1. 浙江工业大学 建筑工程学院，浙江 杭州，310014；2. 重庆交通大学 土木建筑学院，重庆，400074)

近年来，国内外许多学者对饱和成层地基固结变形问题进行了大量的研究。Schiffman等[1-3]开展了简单静载作用下饱和成层地基一维固结研究工作。此后，谢康和等[4-5]获得了变荷载下任意层地基和半透水边界饱和成层地基的一维固结解答。为了更合理地反映地基土特性及附加应力随深度的分布规律，Zhu等[6]研究了随深度变化荷载作用下双层土的固结问题，李冰河等[7-8]采用各天然土层划分多个子层并假定各子层应力应变关系为线弹性的方法，得到了变荷载作用下渗透系数和压缩模量随深度变化的成层地基非线性一维固结问题半解析解。为了合理考虑软土地基的黏弹性特性，蔡袁强等[9-11]通过研究获得变荷载作用下半透水边界黏弹性成层地基的一维固结解答，这为进行现场沉降或沉降速率预测提供了较为有效的计算方法。软土地区修建高速公路等交通基础设施常常采用桥梁跨越不良土体区域，由此产生的桥台后地基长期沉降问题成为关注的焦点。由于桥梁的隔断作用，公路路堤沿纵向出现局部间断，桥台后路堤荷载呈现为半无限条形荷载形式。桥台后路堤荷载作用下地基竖向附加应力非均匀分布，对应的地基沉降亦具有非均匀分布特性。为此，本文作者通过公式推导获得了桥台后软土地基竖向附加应力计算公式以及多级加载条件下路堤荷载的Laplace变换递推公式，基于Terzaghi一维固结理论及Boussinesq弹性力学解答，建立桥台后路堤多级加载下黏弹性饱和成层软土地基固结变形分析方法。通过算例分析阐明了该方法的合理性和可靠性，计算结果可为桥台后软土地基沉降分析提供参考。

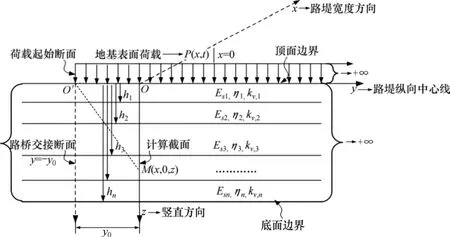
图1 桥台后黏弹性饱和成层软土地基固结计算模型纵断面图Fig.1 Longitudinal section of consolidation analysis model in bridge approach viscoelastic saturated layered soft soils

1 问题的描述

桥台后黏弹性饱和成层软土地基固结求解采用Terzaghi一维固结理论基本假设条件[12]。计算模型纵断面如图1所示，其中：O为空间坐标系原点；O′为路桥交接面与路堤底面(地基表面)中心线交点；x轴为路堤宽度方向；y轴为路堤底面纵向中心线；z轴为竖直方向；y0为计算横截面与路桥交接面在y方向上的距离；P(x，t)为桥台后路堤自重引起的地基表面荷载，其几何特点为x方向(横断面)呈等腰梯形分布，y方向(纵断面)呈半无限均匀分布(即由路桥交接处向正y方向无限延伸)；hi为第i层(i=1，2，…，n)层底z坐标，Esi，ηi，kv,i分别为第 i层(i=1，2，…，n)的压缩模量、黏滞系数和竖向渗透系数。计算模型的初始条件、边界条件以及层间连续条件如下(其中：′为第i层有竖向效应力；t为时间；γw为水的容重)。

2 地基竖向附加应力计算

由于成层软土地基各土层间刚度差异较小，因此，应力扩散效应较小，沿用分层总和法中地基附加应力计算原理而忽略土层应力扩散效应。空间坐标系如图2所示。其中：b为路堤顶部宽度；β为旋转至z轴正方向所夹锐角，逆时针旋转为负，顺时针为正；x为在x轴投影坐标；a为路堤边坡宽度；R1为M点与y轴的距离；y0为计算横截面与路桥交接面y方向距离；h为路堤高度；R为M点与y轴任意点的距离；z为在z轴投影长度。为简化积分表达，图2中坐标原点O始终为路堤底面中心线与计算点M所处横截面xOz交点，该截面与桥台距离为y0，因此，该点坐标为M(x，0，z)。如图2所示，桥台后路堤荷载产生的地基竖向附加应力可以通过左右2个三角形和中间 1个矩形(均匀)分布半无限条形荷载的面积积分得到，该积分可分解为y方向和x方向2步积分。y方向积分范围为，而 x方向积分范围为。具体积分表达式和积分上、下限如表1所示，其中：p0为均布荷载(即三角形荷载最大值)；β1，β2，β3和 β4分别为图 2中地基上任一点M与I，J，C或D点连线与z轴正方向所夹锐角。

表1 横截面上不同类型荷载微分形式(x≥0)Table1 Differential formulation of various loads at transverse sections

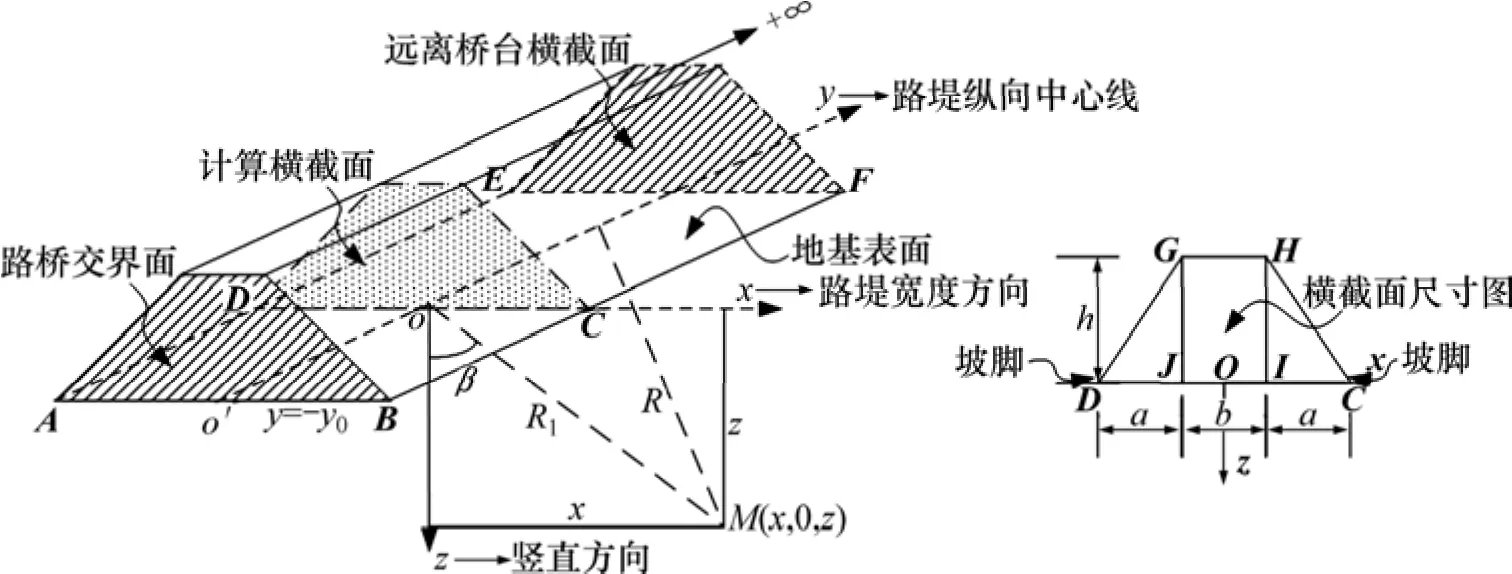
图2 桥台后路堤三维构造模型Fig.2 Configuration of three-dimensional model in bridge-approach embankment

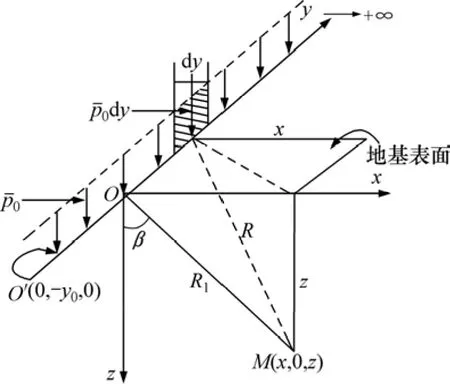
图3 桥台后路堤荷载纵断面积分计算示意图Fig.3 Integral analysis of bridge-approach embankment load at longitudinal section

2.1 荷载沿路堤纵向积分

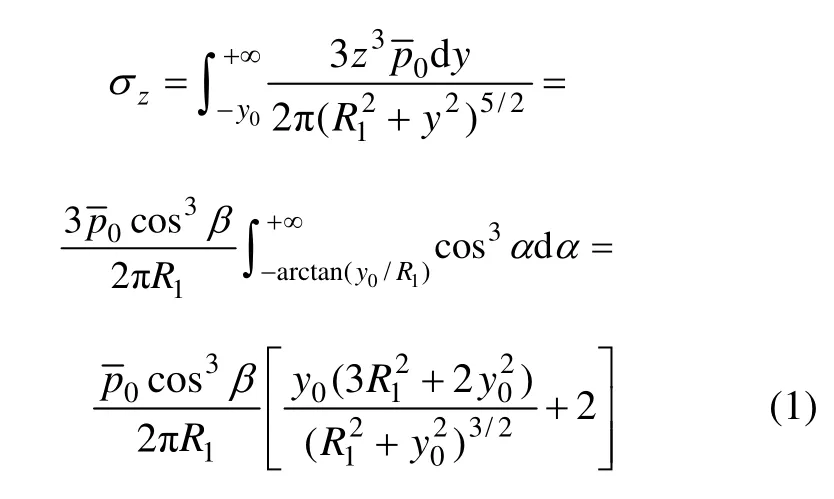
2.2 荷载沿路堤宽度方向积分

2.2.1 矩形分布条形荷载

横截面上矩形分布荷载微分表达式如图4所示，其中：O1为M点在x轴的投影点；O为坐标原点；A为 dx微分段内荷载作用点；C为路堤右侧坡脚；p0为最大荷载集度；为A点处荷载集度；R1为长度。由于地基竖向附加应力关于路堤中心纵断面对称分布，因此，以下只考虑x≥0的情况。将表1中IJGH矩形荷载代入式(1)，积分可得该荷载作用下地基任意位置竖向附加应力：

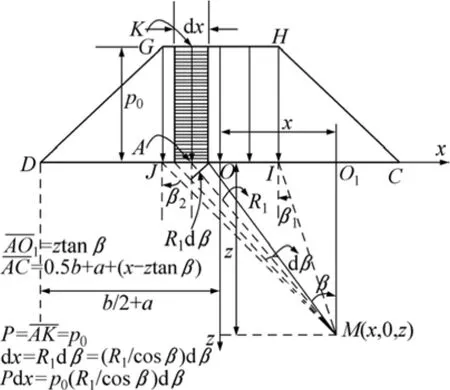
图4 横截面上矩形分布荷载微分表达式Fig.4 Differential formulations of loads in rectangular distribution at transverse section

2.2.2 三角形分布条形荷载

如图5(a)所示，将表1中三角形ΔICH荷载表达式代入式(1)，积分可得相应地基任意位置竖向附加应力：

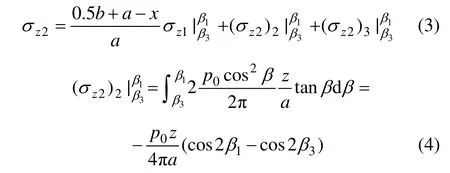
令 y0cos β=ztan γ，则：

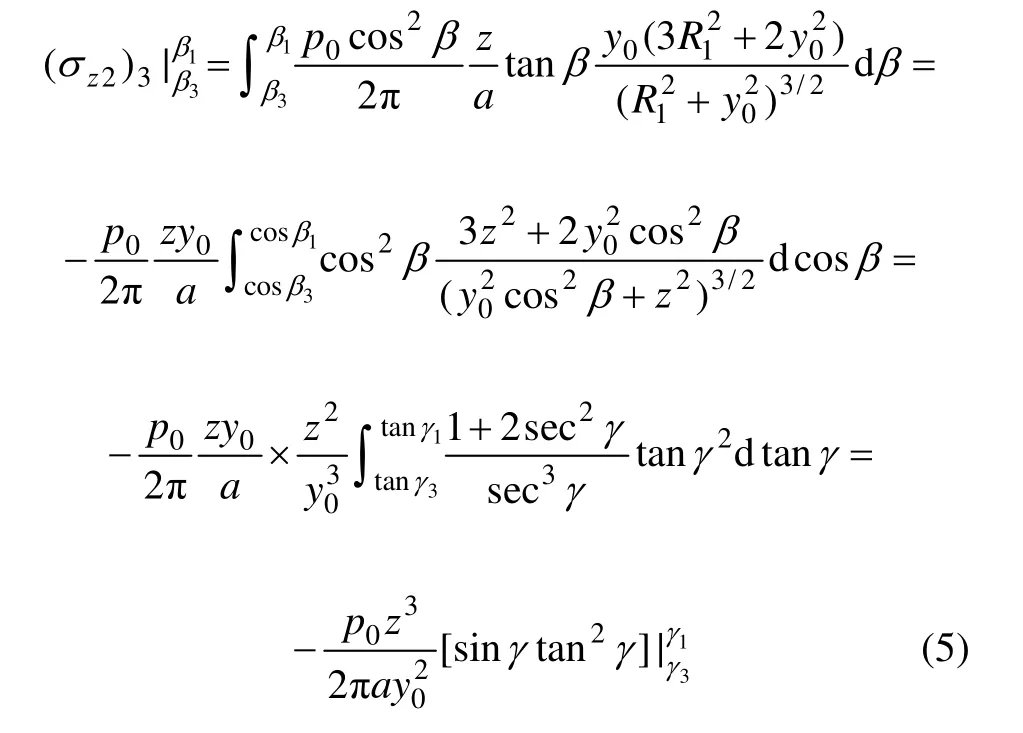
式中：γ为换元积分中间变量。

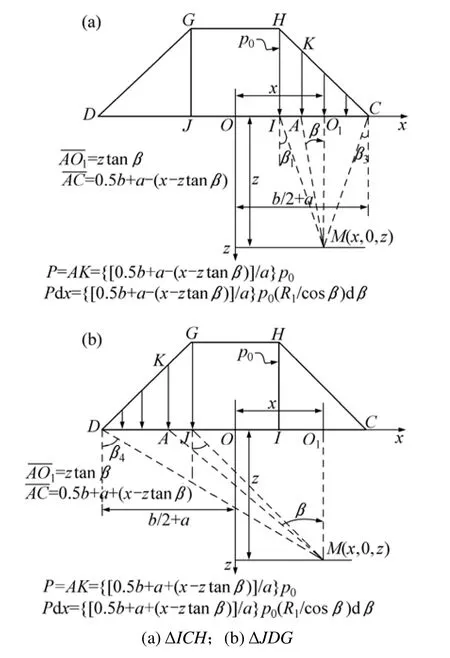
图5 横截面上三角形荷载微分形式Fig.5 Differential formulations of loads in triangular distribution at transverse sections

同理，由图5(b)可以推导得到ΔJDG荷载作用下竖向附加应力为：

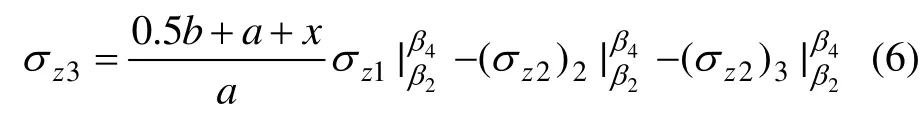
其中： ta nβ3=[x - (b/2+a)]/z；当x≥b/2+a时，β3≥0；当 0≤x＜b/2+a时，β3＜0；而 x≥0时，tanβ4=(x+b/2+a)/z。对应中间变量 γ上、下限 γ1，γ3以及 γ2，γ4可通过三角函数关系计算得到。综上可知，横截面上梯形分布路堤荷载产生的地基竖向附加应力σz计算公式为：

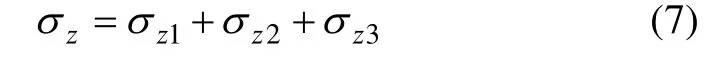
由式(2)~(7)可知，图 1中所示地基表面荷载P(x，t)在桥台后地基中产生的竖向附加应力σz为x，z和y0的函数，即该附加应力在深度方向、纵断面和横断面方向皆呈现为非均匀分布形式。

3 问题求解

3.1 固结方程求解

文献[4]给出的一维黏弹性kelvin体的Terzaghi一维固结微分控制方程为：

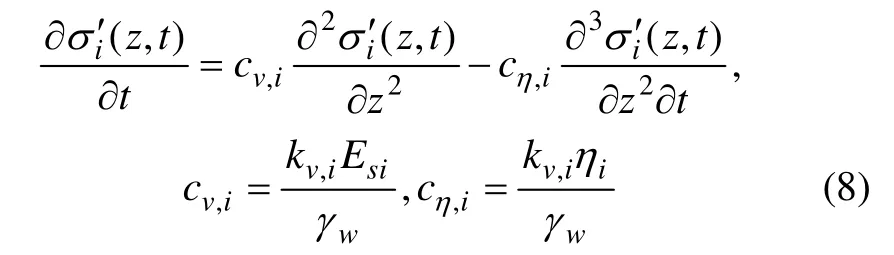
以下根据本文边界和初始条件求解方程(8)。针对时间t对方程(8)进行Laplace变换：

其中：s=ρ+iw，s，ρ，w为Laplace变换参变量。根据初始条件可知z,0)=0，因此，式(9)简化为：

求解方程(10)可得地基第 i土层竖向有效应力Laplace变换解答：

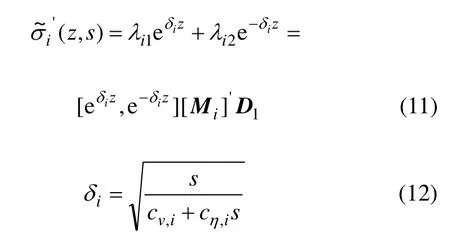
式中：λi1和λi2为第i层土层应力矩阵待定系数。

将有效应力的 Laplace变换解答分别代入层间应力连续条件和流量连续条件的 Laplace变换等式，联立求解可得到应力解系数矩阵Di及其递推公式：

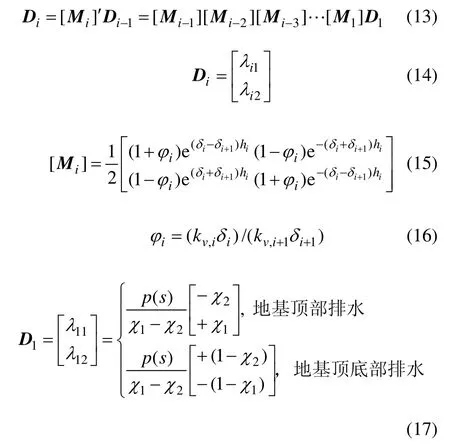
将式(11)进行Laplace逆变换，可获得地基表面无限均布荷载 p0作用下有效应力z,t)与孔压z,t)解答。当竖向附加应力 σz与深度 z满足关系 σz=p0f(z)时 ，根据文献[14]，有效应力z,t)与 孔 压z,t)为：

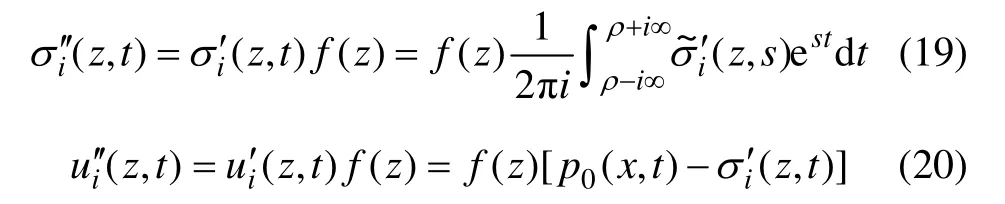
式中，f(z)为σz关于z的分布函数。分别采用式(2)，(3)和(6)计算矩形IJGH分布、三角形ICH分布和三角形JDG分布的单位荷载作用下附加应力 σz1/p0，σz2/p0和σz3/p0，然后，将三者叠加获得图1中点M(x，0，z)的分布函数 f(z)=(σz1+σz2+σz3)/p0。地基总沉降s为各个地基土层沉降Δsi之和：

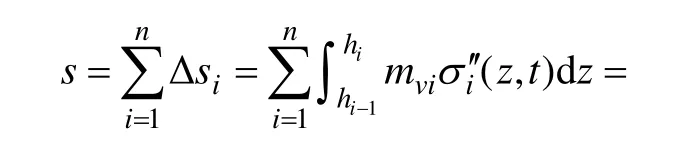
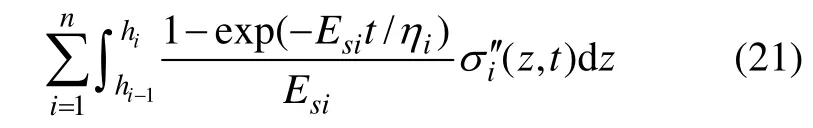
式中：mvi为考虑黏弹性的等效体积压缩系数。

由 于 难 以 通 过 公 式 推 导 方 法 获 得的Laplace逆变换解析解，因此，本文采用常用的Durbin数值方法[15]对式(11)进行Laplace逆变换数值求解。

3.2 路堤多级加载的Laplace变换递推公式

根据桥台后路堤分层填筑现场工况(如图6所示)，给出以下2点假设条件：(1) 第j层填筑时间(加荷时间)为Tcj，对应矩形IJGH区域荷载增量为第i层填土自重pj；(2) 第j个施工间歇期(相邻2个加载阶段的时间间隔)为 Tsj，并且施工间歇期荷载保持恒定。路堤多级加载p(t)表达式为：

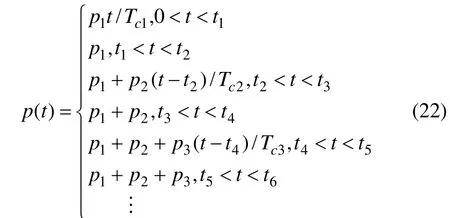
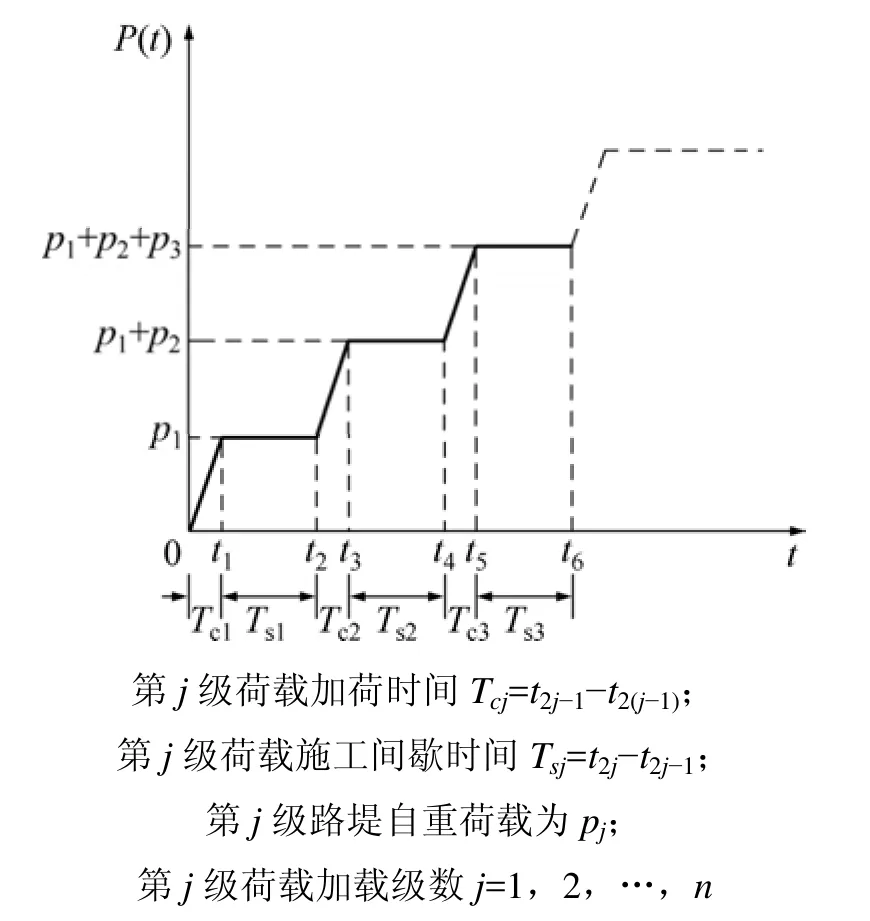
图6 路堤多级加载历时曲线Fig.6 Time history curves of multi-stage embankment loading

tj(j=1，2，3，…，n)为加载时间；ttj为第 j级荷载加载时间和对应的方缸间歇时间之和；t2j-1为第 j级荷载施加完毕时刻；t2j为第 j级施工间歇完毕时的时间，则其中，j=1，2，…，n。

根据 Laplace积分变换定义，可以得到路堤多级加载Laplace变换的一般表达式：

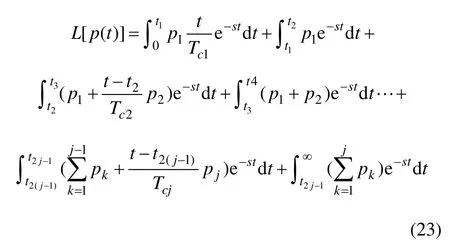
定义以下积分形式：

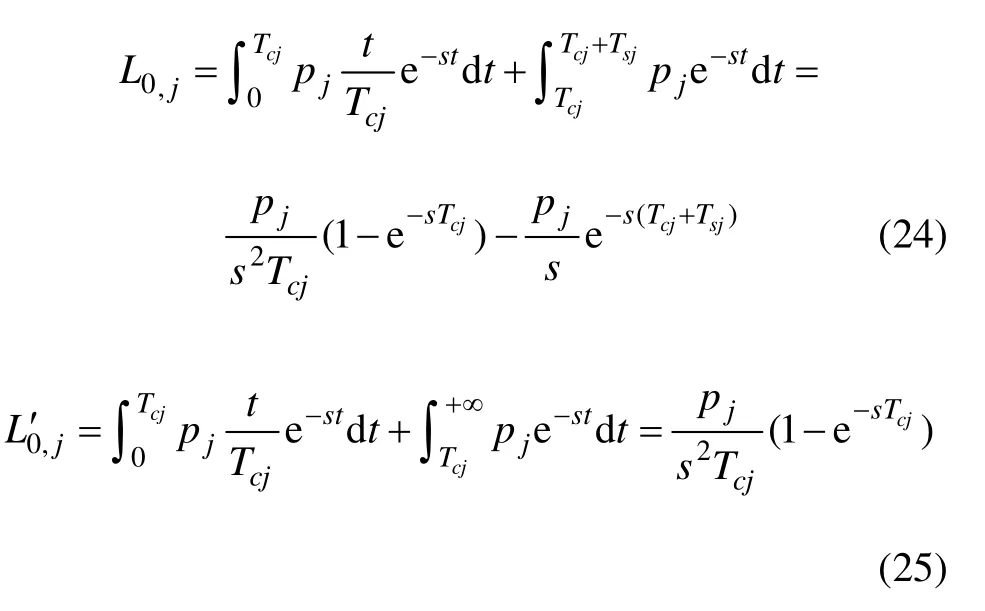
由此得到路堤荷载分1级、2级、…、n级施加的递推公式：

4 算例分析

江苏淮(安)盐(城)高速公路某试验段跨线桥采用桩承式桥台，桥台后饱和成层软土地基模型如图1所示，排水边界条件为单面(顶部)排水。通过室内试验获得成层地基固结参数如表2所示。桥台后路堤高2 m，分 8次填筑，每次厚度 0.25 m，填土容重为 20 kN/m3；桥台后路堤采用等速施工方法填筑，每层填筑时间Tcj=5 d，施工间歇时间Tsj=20 d，因此，路堤竣工时间为200 d。

顶部宽度为b=20 m，边坡坡率为1.0:1.5，由此可得路堤边坡宽度 a=3.0 m。沿着路堤中线在地基表面设置系列沉降监测点，监测工作从路堤填筑时开始，至路堤竣工后480 d结束。依据桥台后路堤多级加载下桥台后饱和成层软土地基一维固结解答，采用Fortran语言编制相应计算程序，针对计入和不计入土层黏性2类情况，对上述工程实例进行沉降预测与实测结果的对比分析。路堤中线下黏弹性饱和成层软土地基表面沉降曲线如图7所示，路堤中线下弹性饱和成层软土地基表面沉降曲线如图8所示。

对比图7和8地表沉降预测结果发现：无论是否计入地基土体黏性特性，越接近桥台处，地表沉降变化幅度越大，越远离桥台，则地表沉降变化幅度越小；计算结果表明：距离桥台距离y≥20 m时，地表沉降达到稳定值并呈现为均匀分布形式。由此可见：地表沉降由非均匀分布过渡到均匀分布反映了桥台截断路堤形成地基应力非均匀分布的影响范围存在有限性。

由图7与图8可知：黏弹性地基地表沉降预测值略小于实测值，而弹性地基地表沉降预测值大于实测值。这是由于描述地基黏弹性的Kelvin体牛顿黏壶起到迟滞变形的作用。计入地基黏性与不计地基黏性相比，其预测值更接近现场实测值。这表明采用黏弹性模型能够较合理地描述软土地基流变特性，并能较准确地预测软土地基沉降。

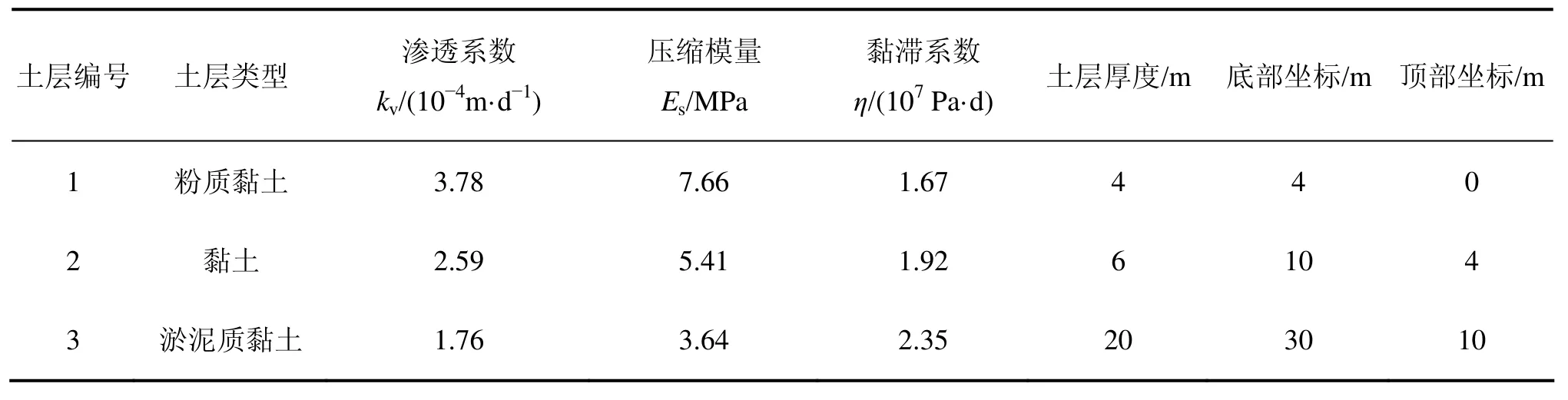
表2 饱和成层软土地基固结参数Table2 Consolidation parameters of saturated layered soft soils

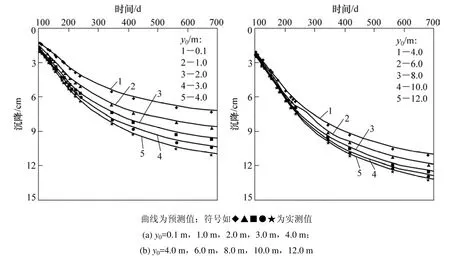
图7 路堤中线下黏弹性饱和成层软土地基表面沉降曲线Fig.7 Settlements at top of viscoelastic saturated layered soft soils under center line of embankment

图8 路堤中线下弹性饱和成层软土地基表面沉降曲线Fig.8 Settlements at top of elastic saturated layered soft soils under center line of embankment

5 结论

(1) 在横截面梯形分布的路堤荷载作用下，桥台后地基竖向附加应力计算公式能够较好地反映地基竖向附加应力沿地基深度和道路纵向的非均匀分布规律。

(2) 多级加载条件下桥台后路堤荷载的 Laplace变换递推公式统一形式能够较好地反映现场路堤分层填筑的实际工况。

(3) 在桥台后路堤多级加载条件下，饱和成层软土地基表面沉降预测值与现场实测值基本一致，表明该固结解答具有合理性和可靠性。

[1] Schiffman R L, Stein J R. One-dimensional consolidation of layered systems[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(4): 1499-1504.

[2] Pyrah I C. One-dimensional consolidation of layered soils[J].Geotechnique, 1996, 446(3): 555-560.

[3] 谢康和. 层状土半透水边界一维固结分析[J]. 浙江大学学报:自然科学版, 1996, 30(5): 567-575

XIE Kang-he. One dimensional consolidation analysis of layered soils with impeded boundaries[J]. Journal of Zhejiang University:Natural Science, 1996, 30(5): 567-575.

[4] 谢康和, 潘秋元. 变荷载下任意层地基一维固结理论[J]. 岩土工程学报, 1995, 17(5): 80-85.

XIE Kang-he, PAN Qiu-yuan. One dimensional consolidation of layered ground under time-dependent loading[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 80-85.

[5] 蔡袁强, 梁旭, 吴世明. 变荷载下半透水边界成层地基的一维固结[J]. 应用数学和力学, 2004, 25(8): 855-862.

CAI Yuan-qiang, LIANG Xu, WU Shi-ming. One-dimensional consolidation of layered soils with impeded boundaries under time-dependent loadings[J]. Applied Mathematics and Mechanics, 2004, 25(8): 855-862.

[6] Zhu G, Yin J H. Consolidation of double soil layers under depth-dependent ramp load [J]. Geotechnique, 1999, 49(3):415-421.

[7] 李冰河, 谢康和, 应宏伟, 等. 变荷载下软粘土非线性一维固结半解析解[J]. 岩土工程学报, 1999, 21(3): 288-293.

LI Bing-he, XIE Kang-he, YING Hong-wei, et al.Semi-analytical solution one-dimensional nonlinear consolidation of soft clay under time-dependent loading[J].Chinese Journal of Geotechnical Engineering, 1999, 21(3):288-293.

[8] 蓝柳和, 谢康和. 半解析法在成层软粘土地基固结问题中的应用[J]. 岩石力学与工程学报, 2003, 22(2): 327-331.

LAN Liu-he, XIE Kang-he. Application of semi-analytical solution into consolidation of layered soft clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2):327-331.

[9] 蔡袁强, 徐长节, 袁海明. 任意荷载下成层黏弹性地基的一维固结[J]. 应用数学和力学, 2001, 22(3): 307-313.

CAI Yuan-qiang, XU Chang-jie, YUAN Hai-ming. Onedimensional consolidation of layered and viscoelastic solids under arbitrary loading[J]. Applied Mathematics and Mechanics,2001, 22(3): 307-313.

[10] 蔡袁强, 梁旭, 郑灶锋, 等. 半透水边界的粘弹性土层在循环荷载下的一维固结[J]. 土木工程学报, 2003, 36(8): 86-90.

CAI Yuan-qiang, LIANG Xu, ZHENG Zao-feng, et al.One-dimensional consolidation of viscoelastic soil layer with semi-permeable boundaries under cyclic loading[J]. Chinese Civil Engineering Journal, 2003, 36(8): 86-90.

[11] 郑灶锋, 蔡袁强, 徐长节, 等. 变荷载下半透水边界成层黏弹性地基的一维固结分析[J]. 浙江大学学报: 工学版, 2005,39(8): 1234-1237.

ZHENG Zao-feng, CAI Yuan-qiang, XU Chang-jie, et al.One-dimensional consolidation of layered and visco2elastic ground under arbitrary loading with impeded boundaries[J].Journal of Zhejiang University: Engineering Science, 2005,39(8): 1234-1237.

[12] Terzaghi K. Theoretical soil mechanics[M]. New York: John Wiley and Sons, 1943: 270-296.

[13] 旷开萃. 高等级公路桥头跳车综合研究和分析[D]. 上海: 同济大学土木工程学院, 2002: 20-26.

KUANG Kai-cui. Investigation and analysis on the bridge-approach bump on the highway[D]. Shanghai: Tongji University. College of Civil Engineering, 2002: 20-26.

[14] 赵维炳, 施建勇. 软土固结与流变[M]. 南京: 河海大学出版社, 1996: 34-62.

ZHAO Wei-bing, SHI Jian-yong. Consolidation and rheology on soft soils[M]. Nanjing: Hohai University Press, 1996: 34-62.

[15] Durbin F. Numerical inversion of Laplace transform: An efficient improvement to Dubner and Abate’s method[J].The Computer Journal, 1974, 17(4): 371-376.