短波随机不平顺对列车-板式无砟轨道-路基系统振动特性的影响
2011-06-01徐庆元曹扬风周小林
徐庆元,曹扬风,周小林
(中南大学 土木建筑学院,湖南 长沙,410075)
无砟轨道技术是一项现代化铁路技术,具有良好的运营功能并可取得明显的经济效益。高速铁路采用无砟轨道后,轨道稳定性相应增强,列车运行的平稳性和安全性大大提高。由于取消了易产生残余变形的道砟,大大降低了轨道几何状态变化的速率, 维修工作量可大大减少,有利于列车高密度运行。随着无砟轨道技术的发展,无砟轨道已在国外高速铁路上得到广泛采用。我国新建和在建高速客运专线如京津城际高速铁路、京沪高速铁路、武广客运专线、郑西客运专线、哈大客运专线等,均大量采用无砟轨道技术,时速350 km/h京津城际高速铁路现已正式投入运营。目前,国内外[1-11]虽对列车在板式无砟轨道上高速运行时系统振动特性进行了研究,但大多针对确定性不平顺及中长波随机不平顺,对短波随机不平顺对列车-板式无砟轨道-路基系统动力特性的影响特别是动应力特性影响研究较少。为此,本文作者建立列车-板式无砟轨道-路基时变耦合动力学模型,用 Matlab编制相应的计算程序,并用所编制的计算程序,分析列车高速运行时,短波随机不平顺对列车-板式无砟轨道-路系统振动特性的影响,并对不同种类随机不平顺对列车-板式无砟轨道-路基系统动力特性的影响进行对比研究。
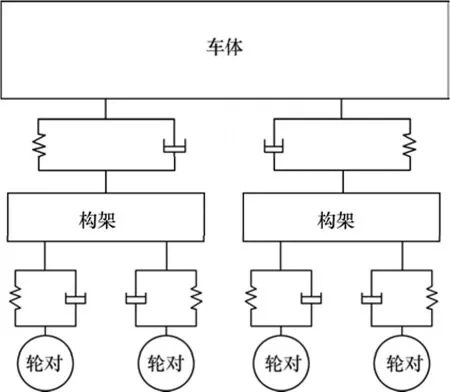
图1 车辆垂向振动模型Fig.1 Vertical vibration model of vehicle
1 车-无砟轨道-路系统动力学模型
1.1 机车车辆模型
与列车竖向振动相关的自由度包括车体及构架的沉浮和点头,以及轮对的沉浮,即每辆四轴车有 10个自由度(见图 1),对于机车车辆组成的车列,则为10×m个自由度(其中,m为机车车辆数)。
1.2 板式无砟轨道及路基模型
钢轨、轨道板、底座均以梁单元模拟,连接钢轨与轨道板的扣件、连接轨道板与底座板的CA砂浆以线性弹簧-阻尼单元模拟,路基模型采用文克尔假定,也以线性弹簧-阻尼单元模拟(见图2)。
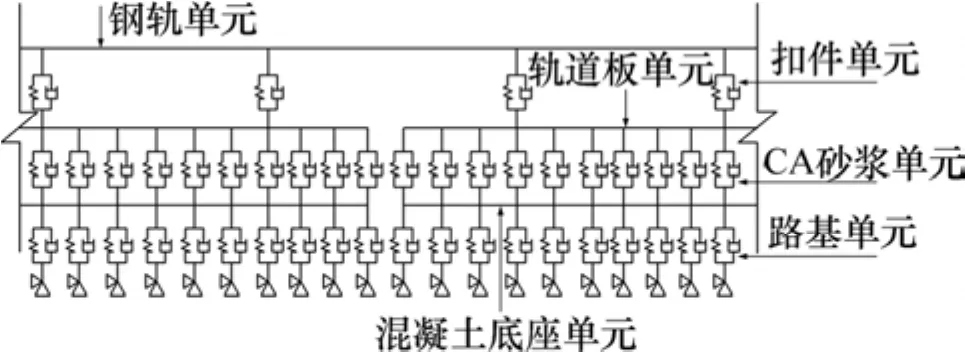
图2 路基上板式无砟轨道动力学模型Fig.2 Dynamic mechanical model of slab track on subgrade
1.3 轨道不平顺模型及其数值模拟
在正常情况下,无砟轨道不平顺组成成分十分复杂,含有各种波长,但其统计有一定的特征,即所谓的随机不平顺。
由于我国还缺乏高速铁路无砟轨道谱,本文采用德国适用于 250 km/h以上的高速铁路低干扰功率谱密度来进行中长波(波长为 1~50 m)随机不平顺的模拟[12],其表达式为:

式中:S(Ω)为功率谱密度;Ω为空间频率;Av为粗糙度常数,4.032×10-7m·rad;Ωc为截断频率,0.824 6 rad/m;Ωr为截断频率,0.020 6 rad/m。
德国低干扰功率谱密度以中长波为主,不能很好地考虑短波随机不平顺对板式无砟轨道动力学特性的影响。根据翟婉明及作者的研究,波长为0.01~1 m的短波随机不平顺对轨道动力特性有较大影响。为了合理考虑短波随机不平顺对板式无砟轨道动力学特性的影响,本文采用的随机不平顺模型除了考虑中长波随机不平顺外,还叠加了短波随机不平顺。波短不平顺功率谱密表达式为[12]。

式中:S(f)为功率谱密度,mm2·m/次;f为空间频率,1/m。
采用翟婉明等[1]介绍的方法进行随机不平顺的数值模拟。首先根据轨道随机不平顺功率谱求出频谱的幅值和随机相位,然后,通过傅里叶逆变换得到轨道不平顺的时域模拟样本。
列车起始位置全部置于平顺地段,行驶一段距离(本文取10 m)后进入随机不平顺地段,最后驶出随机不平顺地段,再次进入平顺地段。
由于平顺地段不平顺的一阶及二阶导数均为 0,而根据轨道随机不平顺功率谱通过傅里叶逆变换得到轨道不平顺的时域模拟样本起终点的一阶导数及二阶导数很难做到同时为0(或接近0)。列车直接由平顺地段进入随机不平顺地段,将产生很强的动力效应。因而在随机不平顺和平顺地段之间需要一过渡地段,过渡段要满足在过渡段起终点一阶导数及二阶导数充分小,列车经过过渡段后,动力学响应足够小。
参考大型车辆动力学通用软件ADAMS的做法,将随机不平顺起始点作为起始过渡段始端,并将其不平顺幅值置为0,在离随机不平顺起始点一段距离(本文取 20 m)范围以便选取起始过渡段终端点,将起始过渡段始端与起始过渡段终端连线作为起始过渡段,然后,检查起始过渡段起点和起始过渡段终点的一阶及二阶导数。若20 m之内所有点均不能满足作为起始过渡段终点的要求,则重新生成另一时域模拟样本,再次进行起始过渡段终端点的选取,直到生成合乎条件的随机不平顺样本为止。终端过渡段生成原理及方法与起始过渡段的类似。随机不平顺起始过渡段及终端过渡段生成后,整个随机不平顺生成工作结束。
1.4 轮轨关系模型
采用文献[12]中的轮轨关系模型,轮轨垂向作用力由赫兹非线性弹簧接触理论所确定:

式中:G 为轮轨接触常数,m/N2/3;Zw(j,t)为 t时刻第j位车轮的位移,m;Zr(j,t)为t时刻第j位车轮下钢轨的位移,m;Z0(t)为轮轨界面存在的不平顺。
1.5 列车-板式无砟轨道-路系统动力学模型初始条件
为了正确模拟轮轨力为零的“脱空”状态,除了随机不平顺荷载外,还在机车车辆各部件的质心处施加自重荷载,在自重荷载作用下的静平衡位置为初始条件,即先在自重荷载作用下进行静力计算,计算结果作为动力分析的初始条件。
1.6 列车-板式无砟轨道-路系统动力学模型竖向振动方程组的建立及求解
机车车辆空间振动总势能包括车体、构架和轮对的惯性力势能和重力势能以及机车车辆悬挂系统的弹性应变能和阻尼力势能。据弹性系统动力学总势能不变值原理,对机车车辆总势能的表达式进行一阶变分,并运用形成矩阵的“对号入座”法则即可得到机车车辆竖向振动方程组。
运用弹性系统动力学总势能不变原理和形成矩阵的“对号入座”法则分别组集钢轨、轨道板、底座及连接弹簧-阻尼单元的刚度矩阵、阻尼矩阵、质量矩阵以及节点荷载列阵,可得板式无砟轨道及路基系统竖向振动方程组。
以轮轨关系模型为纽带,采用文献[13]中介绍的交叉迭代法进行机车车辆竖向振动方程组和板式无砟轨道及路基系统振动方程组求解。
2 列车-板式无砟轨道-路基耦合动力学模型验证
由于缺乏高速铁路无砟轨道动力学实测数据,本文对机车车辆动力模型、无砟轨道动力模型、随机不平顺模型分别进行验证,达到间接验证的目的。验证1针对机车车辆动力模型,验证2针对无砟轨道动力模型,验证3针对随机不平顺模型。
2.1 验证1
铁道科学研究院于1994年在广深准高速铁路测量了不同波长和波深的轨道几何不平顺对准高速车辆振动加速度的影响,准高速车辆参数及轨道参数见文献[12]。在不同试验工况下,试验实测值、本文力学模型理论计算值、文献[12]中理论计算值结果对比见表1。
从表1可见:试验实测值、本文力学模型理论计算值、文献[12]理论计算值较吻合,证明本文机车车辆模型的正确性。
2.2 验证2
路基上板式无砟轨道系统,钢轨为60轨,扣件为高弹性扣件,其刚度为 35 kN/mm,轨道板间断,轨道板宽度为2.4 m,轨道板厚度为0.19 m,轨道板长度为5 m,CA砂浆厚度为5 cm,弹性模量为400 MPa,轨道板弹性模量为34.5 GPa,底座板连续,底座板宽度为 2.8 m,厚度为 0.3 m,底座板弹性模量为 32.5 GPa。作用一正弦形荷载,荷载作用在轨道板中间对应钢轨节点上,荷载函数表达式为:

其中:v=83.3 m/s,分别用Ansys和自编Matlab程序对此工况进行计算。加载点轨道板和底座板加速度时程曲线对比见图3和图4。
从图 3和图 4可以看出:自编程序计算结果和ANSYS软件计算结果较吻合,证明本文无砟轨道动力模型的正确性。

图3 加载点轨道板加速度时程曲线比较Fig.3 Comparison of time history of slab acceleration at load point position
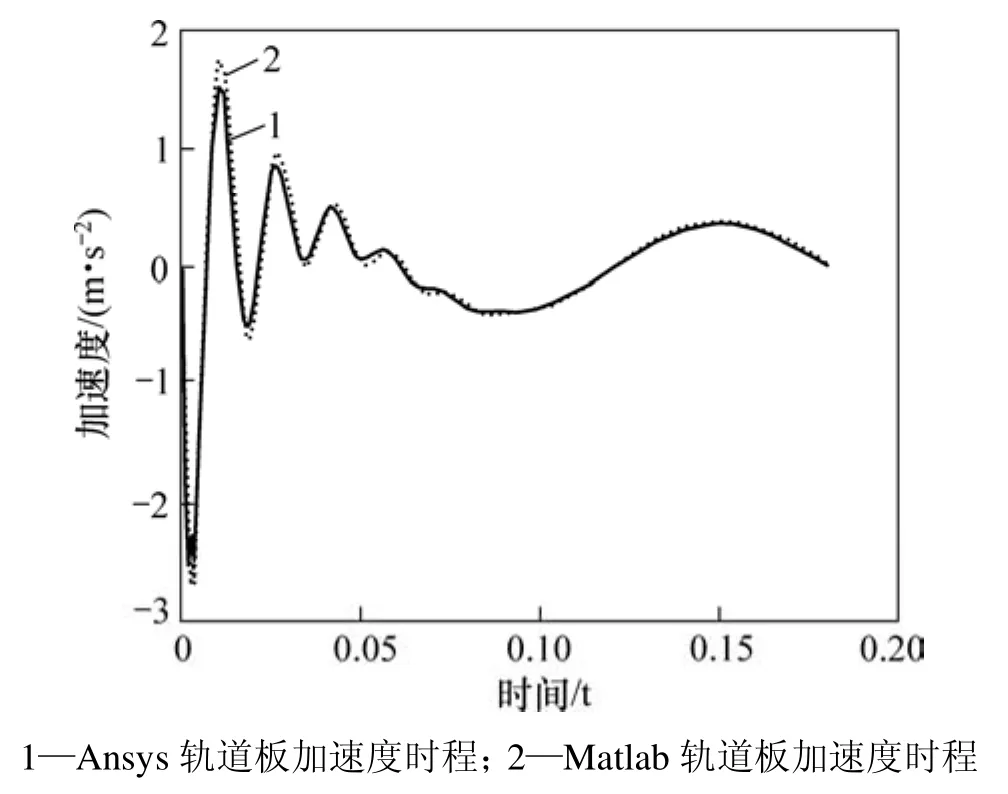
图4 加载点底座板加速度时程曲线比较Fig.4 Comparison of time history of concrete basement acceleration at load point position

表1 广-深线车体垂向振动加速度实测及理论计算对比表Table1 Vehicle vertical acceleration comparison between field test data and theoretic calculation in Guang-Shen line
2.3 验证3
采用德国适用于 250 km/h以上的高速铁路低干扰功率谱密度来进行中长波随机不平顺的模拟。理论功率谱密度表达式见式(1),根据理论功率谱密度模拟的随机不平顺样本见图5。图6所示为理论功率谱密度与样本功率谱密度的差值。
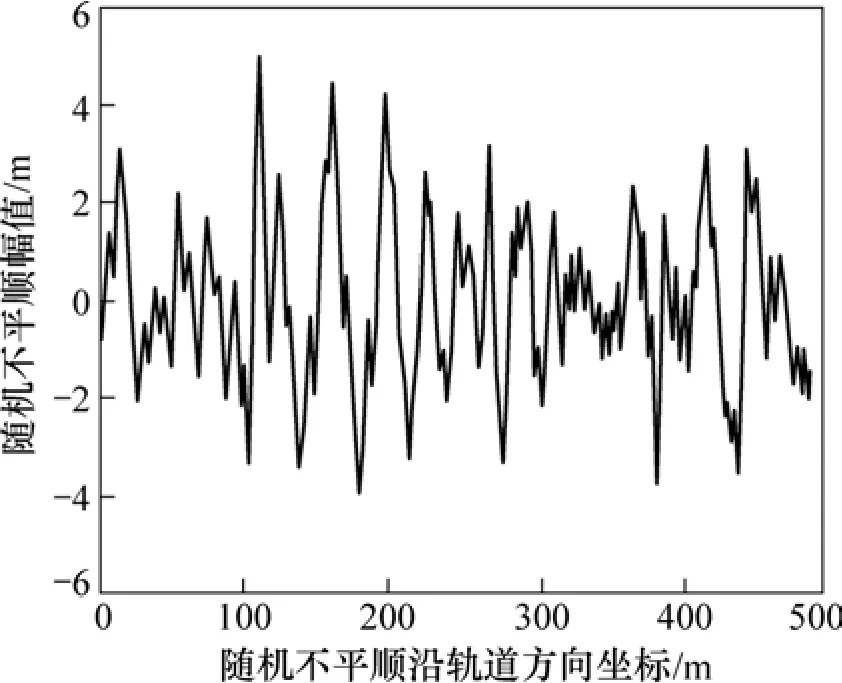
图5 随机不平顺样本Fig.5 Sample of random irregularity
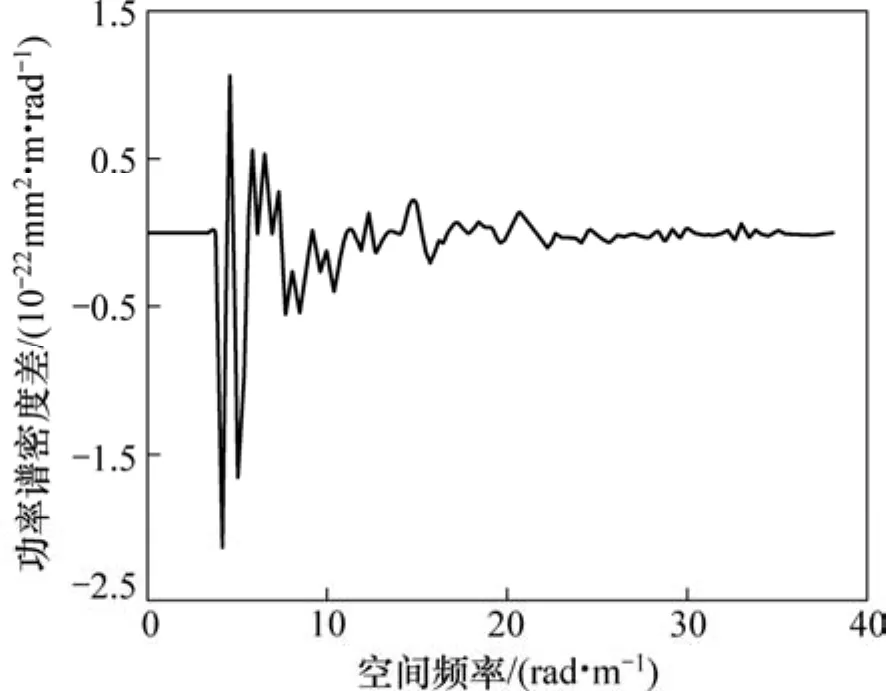
图6 理论与样本功率谱密度差Fig.6 Error between theoretical and sample power spectral density
从图6可以看出:理论与样本功率谱密度差值很小,证明随机不平顺样本模拟的正确性。
3 计算算例
3.1 计算条件
以1动+4拖高速动车组以300 km/h速度通过路基上单元板式无砟轨道为例,研究短波随机不平顺对车-无砟轨道-路系统振动特性影响。高速动力组参数见文献[8],轨道主要计算参数如表2所示。
采用式(1)轨道谱进行中长波轨道随机不平顺模拟,采用式(2)轨道谱进行短波随机不平顺模拟,随机不平顺长度取为400 m。
轨道不平顺考虑4种工况:综合考虑短波及中长波随机不平顺(工况 1)、仅考虑短波随机不平顺(工况2)、仅考虑中长波随机不平顺(工况3)及不考虑随机不平顺(工况4)。
时间步长取为 6×10-5s,每一时间步长移动 5 mm,以合理考虑短波随机不平顺的影响,不同随机不平顺工况下列车-板式无砟轨道-路系统竖向振动响应比较见表3。
3.2 计算结果分析
(1) 短波随机不平顺对车体垂向加速度、路基最大压应力影响很小,如车体最大垂向加速度仅增加0.001 m/s2,路基最大压应力仅增加0.001 MPa。
(2) 短波随机不平顺对钢轨最大垂向加速度、轨道板最大垂向加速度、底座板最大加速度、轮轨最大垂向力及CA砂浆最大竖向压应力有很大的影响,而且影响比中长波随机不平顺的大。如短波随机不平顺引起的钢轨振动加速度为中长波随机不平顺引起的20倍以上,短波随机不平顺引起的轨道板振动加速度为中长波随机不平顺引起的5倍以上,短波随机不平顺引起的底座板振动加速度为中长波随机不平顺引起的2倍以上,短波随机不平顺引起的轮轨最大垂向力及CA砂浆最大竖向压应力动力幅度增加值也为中长波随机不平顺引起的动力幅度增加值的2倍以上。
(3) 短波随机不平顺对轨道板纵向最大弯曲动应力、底座板纵向最大弯曲动应力及扣件最大竖向动压应力有一定的影响,但其影响比中长波随机不平顺的小。如短波随机不平顺引起的扣件压力动力幅度增加值约为中长波随机不平顺引起的30%左右,短波随机不平顺引起的轨道板最大弯曲动应力幅度增加值约为中长波随机不平顺引起的50%左右,短波随机不平顺引起的底座板最大弯曲动应力幅度增加值约为中长波随机不平顺引起的20%左右。

表2 板式无砟轨道计算参数Table2 Calculation parameter of slab track

表3 不同随机不平顺工况计算结果比较Table3 Comparison among different load case of random irregularity
4 结论
(1) 短波随机不平顺对车体垂向加速度、路基最大压应力影响很小,在进行车体及路基动力学分析时,可以忽略短波随机不平顺影响,仅考虑中长波随机不平顺。
(2) 短波随机不平顺对钢轨最大垂向加速度、轨道板最大垂向加速度、底座板最大加速度、轮轨最大垂向力及CA砂浆最大竖向压应力有很大的影响,而且其影响比中长波随机不平顺的大。
(3) 短波随机不平顺对轨道板纵向最大弯曲动应力、底座板纵向最大弯曲动应力及扣件最大竖向压应力影响虽比中长波随机不平顺的小,但为了提高精度,仍有必要考虑其影响。
(4) 短波不平顺对高速铁路运营有较大的影响,短波不平顺还是引起噪音的主要原因。为了降低短波不平顺的危害,高速铁路钢轨定期打磨十分必要。
[1] 翟婉明, 韩卫军, 蔡成标, 等. 高速铁路板式轨道动力特性研究[J]. 铁道学报, 1999, 21(6): 64-69.
ZHAI Wan-ming, HAN Wei-jun, CAI Cheng-biao, et al.Dynamic properties of high speed railway slab tracks[J]. Journal of the China Railway Society, 1999, 21(6): 64-69.
[2] 蔡成标, 翟婉明, 王开云. 遂渝线路基上板式轨道动力性能计算及评估分析[J]. 中国铁道科学, 2006, 27(4): 17-21.
CAI Cheng-biao, ZHAI Wan-ming, WANG Kai-yun. Calculation and assessment analysis of the dynamic performance for slab track on Sui-Yu railway[J]. China Railway Science, 2006, 27(4):17-21.
[3] 蔡成标. 无砟轨道动力学理论及应用[J]. 西南交通大学学报,2007, 42(3): 255-261.
CAI Cheng-biao. Dynamics of ballastless track and its application[J]. Journal of Southwest Jiaotong University, 2007,42(3): 255-261.
[4] 向俊, 赫丹, 曾庆元. 横向有限条与无砟轨道板段单元的车轨系统竖向振动分析法[J]. 铁道学报, 2007, 29(4): 64-69.
XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J]. Journal of the China Railway Society, 2007, 29(4): 64-69.
[5] 赫丹, 向俊, 曾庆元. 一种无碴轨道动力学建模的新方法[J].中南大学学报: 自然科学版, 2007, 38(6): 1206-1211.
HE Dan, XIANG Jun, ZENG Qing-yuan. A new method for dynamics modeling of ballastless track[J]. Journal of Central South University: Science and Technology, 2007, 38(6):1206-1211.
[6] 向俊, 曹晔, 刘保钢. 客运专线板式无碴轨道动力设计参数[J]. 中南大学学报: 自然科学版, 2007, 38(5): 981-986.
XIANG Jun, CAO Ye, LIU Bao-gang. Dynamic parameters of slab track of passenger transport line[J]. Journal of Central South University: Science and Technology, 2007, 38(5): 981-986.
[7] XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis theory of spatial vibration of high-speed train and slab track system[J].Journal of Central South University of Technology, 2008, 15(1):121-126.
[8] 宣言, 王澜. 客运专线曲线线路车线耦合系统动力学性能与无砟轨道结构振动响应的仿真研究[D]. 北京: 铁道科学研究院, 2005: 32-34.
XUAN Yan, WANG Lang. Simulation research on the dynamic characteristics of vehicle-track coupling system on curved track and the vibration response of ballastless track structure of passenger dedicated line[D]. Beijing: China Academy of Railway Sciences, 2005: 32-34.
[9] Verbic B. Investigating the dynamic behavior of rigid track[J].Rail Gazette International, 1997, 153(9): 585-586.
[10] Steenbergen M J M M, Metrikine A V, Esveld C. Assessment of design parameters of a slab track railway system from a dynamic viewpoint[J]. Journal of Sound and Vibration, 2007, 306(1):361-371.
[11] Yen S T, Lee Y H. Parameter identification and analysis of a slab track system using 3D ABAQUS program[J]. Journal of Transportation Engineering, 2007, 133(5): 288-297.
[12] 翟婉明. 车辆-轨道耦合动力学. 第2版[M]. 北京: 中国铁道出版社, 2002: 146-147.
ZHAI Wan-ming. Vehicle-track coupling dynamics. Second Edition[M]. Beijing: China Railway Publishing House, 2002:146-147.
[13] 雷晓燕. 轨道力学与工程新方法[M]. 北京: 中国铁道出版社,2002: 69-71.
LEI Xiao-yan. New methods in railroad track mechanics &technology[M]. Beijing: China Railway Publishing House, 2002:69-71.
