线性节理对岩石电磁辐射传播的影响
2011-06-01万国香李夕兵王其胜
万国香,李夕兵,王其胜
(1. 嘉应学院 物理与光信息科技学院,广东 梅州,514015;2. 中南大学 资源与安全工程学院, 湖南 长沙, 410083;3. 嘉应学院 土木工程系,广东 梅州,514015)
近年来,岩石破裂过程中的电磁辐射现象已引起国内外学者的关注。作为一种无损监测技术,电磁辐射被广泛应用于岩石、混凝土等材料的破坏研究。为了解释岩石破裂的电磁信号,人们提出了裂纹尖端电子发射、微破裂产生电偶极子及其天然半导体效应、压电压磁效应及动电效应等关于电磁辐射的机理[1-5]。如:Warwick等[6]试图以压电性解释1960年智利地震时所观测到的电磁现象;Huang等[7]结合压电效应和断层位错模型研究了同震电信号的产生机理;虽然Brady等[8]认为压电效应对光辐射的贡献不大,但他们同时也认为含压电晶体的岩石发射的某些频段的电磁波远比无压电晶体的岩石所发射的电磁波强。这些研究大多数是针对完整岩石进行的,事实上,岩体作为一种非均匀脆性介质,其中含有大量的裂隙、节理等缺陷,研究这些缺陷对不同频率段的电磁信号的影响对于更好地了解电磁辐射的传播过程以及在现场探测岩石破裂电磁信号具有积极意义。Makarets等[9]研究了一个含有裂纹的有限大的压电晶体,研究结果表明,电磁辐射强度作为频率的函数有多个极值,波长由晶体和裂纹速度决定,并且集中于光谱的长波区域。Koshevaya等[10]基于岩石的压电特性对地震电磁现象进行模拟研究,研究32晶系压电晶体在机械应力的作用下裂纹开始匀速运动,裂纹附近区域的非静态应力产生了非静态的极化电流,从而进一步产生了电磁波。万国香等[11]研究了岩体中应力波所伴随的电磁辐射特征,以及节理面前后电磁辐射强度的变化。在此,本文作者在前期工作的基础上,基于含石英岩体的压电性,研究节理对岩体中电磁辐射传播的影响及节理的黏性系数等参数对电磁辐射强度所产生的影响。
1 压电本构关系
材料在受到应变时称为电极化的这种所谓正压电效应,在实验上表现为应变介质表面出现束缚电荷,当应变反号时,极化也随之反号。也就是说,当材料发生形变时,固体的原子(以及原子内部的电子)也随之发生位移,这种位移在介质内产生微观电偶极矩,而在某些晶体结构中,这些偶极矩组合出1个平均的宏观矩(即电极化)。
在压电体内,压电本构方程为[12]:
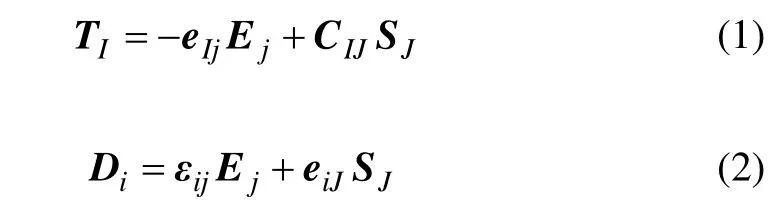
式中:TI和 SJ分别代表应力张量和应变张量;Ej和Di分别为电场强度和电位移矢量;CIJ,eiJ和εij分别为弹性刚度张量、压电张量和介电极化张量。式中下标采用爱因斯坦求和方式进行标记。
1.1 纵波下的电磁辐射强度
设定含石英等压电介质的岩体具有6 mm晶系。选择坐标轴x,y和z分别与晶轴X,Y和Z重合(下同)。假设介质中有 1个 x偏振、x传播的质点位移(纵波)为 u = xˆcos(ωt - kx), 与 之 相 对 应 的 应 变 场=ksin(ωt - kx),由压电本构方程,并考虑到电磁辐射信号在岩体介质中传播时会衰减,引入衰减因子e-ηr[13],得到纵波下电磁辐射为[11]:
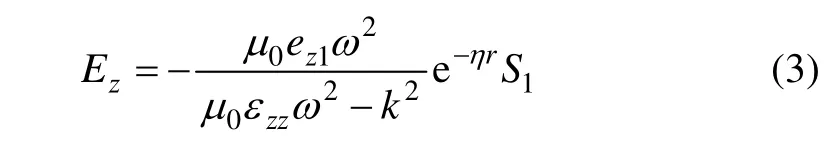
其中,ω为频率;k为波数;r为传播距离;η为衰减系数;ε为介电常数;µ0为磁导率;ρ为岩体电阻率;t为时间。
衰减系数η与介电常数ε、磁导率µ0和电磁波的频率ω有关,可表示成:
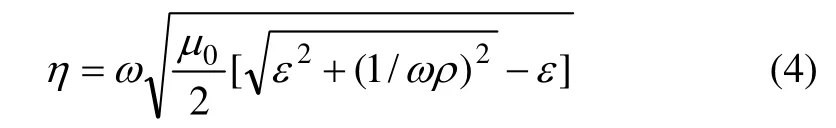
1.2 横波下的电磁辐射强度
假设介质中有z偏振、x传播的质点位移(SV波),根据压电本构关系式(1)和(2)可得[11]:

对于y偏振、x传播的质点位移(SH波),不产生电磁辐射。
1.3 32晶系中的电磁辐射强度
为了与6 mm晶系对照,对于32晶系,也考虑x偏振、x传播的质点位移(纵波)和z偏振、x传播的质点位移(SV波),它们所产生的电磁辐射如下[11]:

2 应力波在节理处的透射解
为了简单,考虑1个在xOz平面内传播的应力波S(1)垂直入射到节理面,不考虑斜入射,取分界面为zOy面。为了与6 mm和32晶系的坐标一致,取x为纵坐标,z为横坐标。当应力波垂直入射到界面时,通过同时发生的透反射作用,通常产生反射应力波S(2)和透射应力波S(3),三者可表示为:
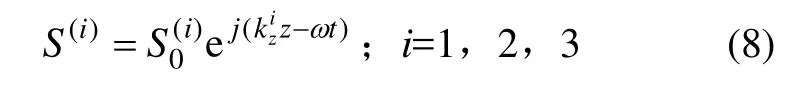
根据线性位移不连续模型,对于垂直入射的纵波和SV波,边界条件为:
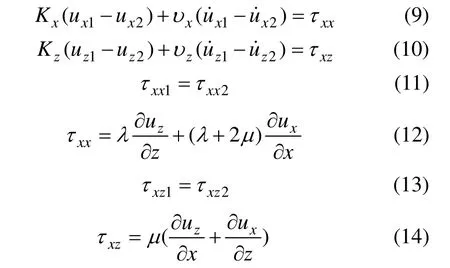
对于SH波,边界条件为:

其中:Kx,Ky和Kz分别为节理的法向和切向刚度;µ和λ分别为泊松比和剪切模量;xυ和zυ分别为节理的方向和切向黏性系数;τ为剪应力;下标1和2分别表示节理面两侧的介质1和2。
由以上分析可得纵波垂直入射到节理面的透射解为[14]:
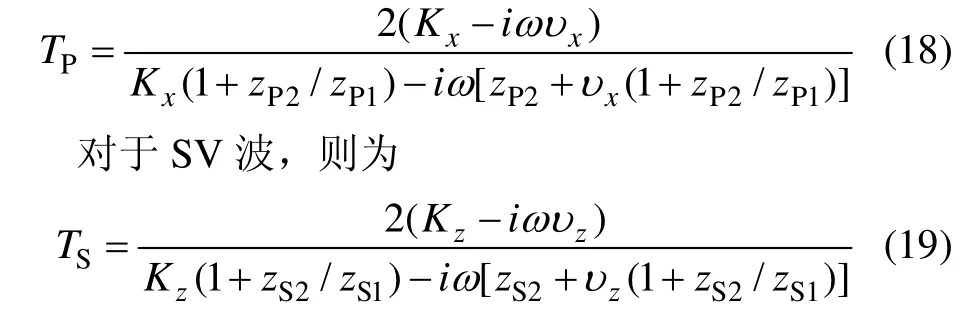
式中:对于线性变形节理,Kx和Kz分别等于节理的初始法向刚度Kx0和初始切向刚度Kz0;下标P和S分别表示纵波和横波;介质1中纵波波阻抗 zP1=ρ1vP1,介质1中横波阻抗 zS1=ρ1vS1(ρ1为介质1的密度;vP1为介质1中的纵波速度;vS1为介质1中的横波速度),其他依此类推(SH波透射解与SV波相同,只需将式(19)中 Kz换成 Ky即可)。
3 节理面前后电磁辐射强度的变化
分2种情况讨论:当节理面两侧介质1和2岩体性质完全相同时,假定介质1和2均为6 mm晶系;当节理面两侧介质不同时,假定介质1具有6 mm晶系,介质2具有32晶系。
3.1 节理面两侧介质性质相同时电磁辐射强度变化
3.1.1 纵波下电磁辐射强度变化
根据式(3)和式(18),可得纵波作用下岩体电磁辐射在节理面前后的表达式为:

将式(21)除以式(20)即得到节理面前后纵波作用下电磁辐射强度的变化:
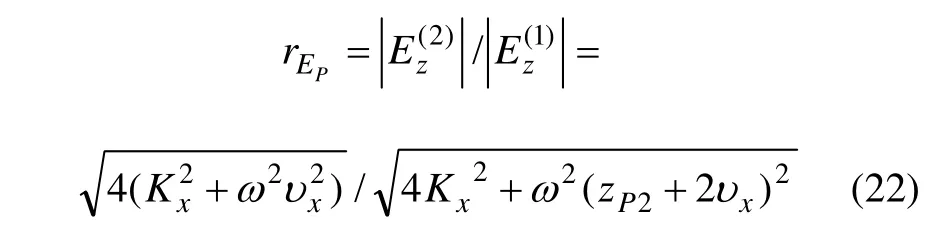
3.1.2 横波下电磁辐射强度变化
根据式(5)和式(19)并引入衰减因子erη-(以下均考虑衰减),可得到岩体在横波作用下电磁辐射在节理面前后的表达式:
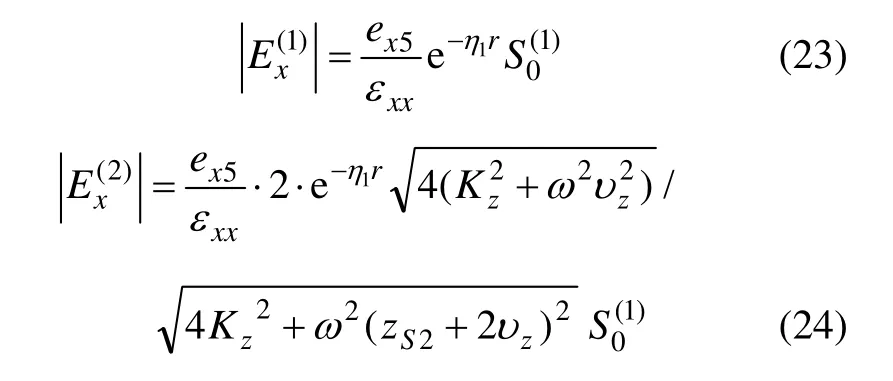
将式(24)除以式(23)即得到节理面前后横波下电磁辐射的强度变化:
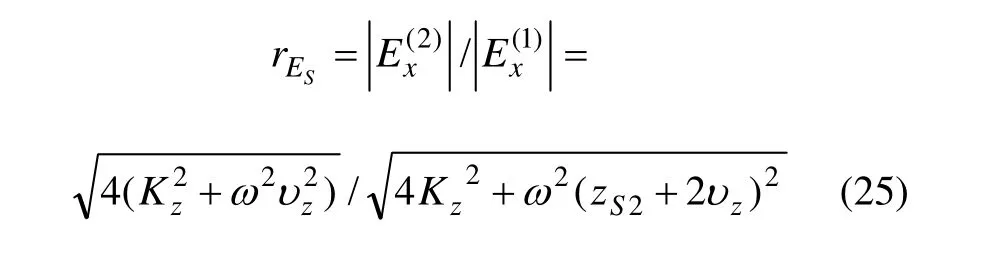
3.2 节理面两侧介质性质不同时电磁辐射强度变化
3.2.1 纵波下电磁辐射强度变化
根据式(3),(6)和(18)可得纵波作用下岩体电磁辐射在节理面前后的表达式为:
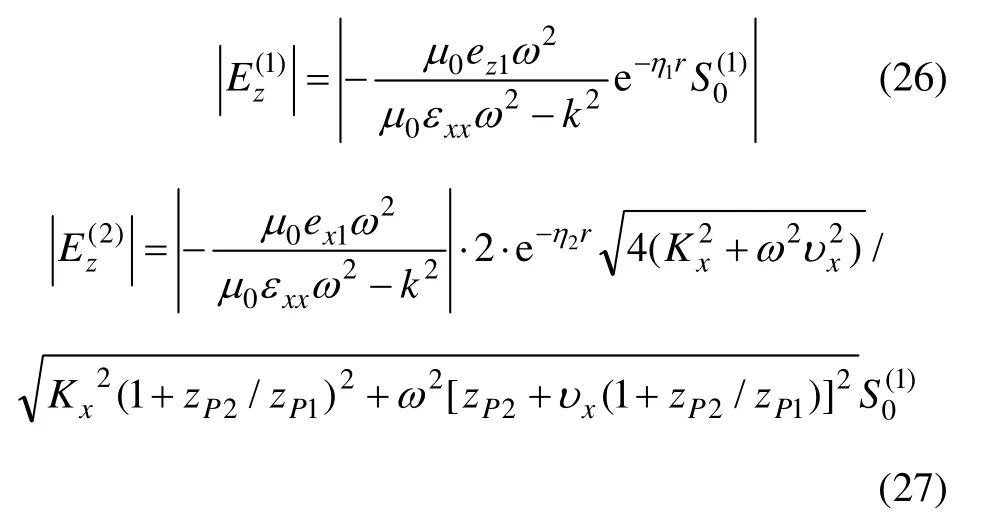
将式(27)除以式(26)即得到节理面前后纵波下电磁辐射的强度变化:
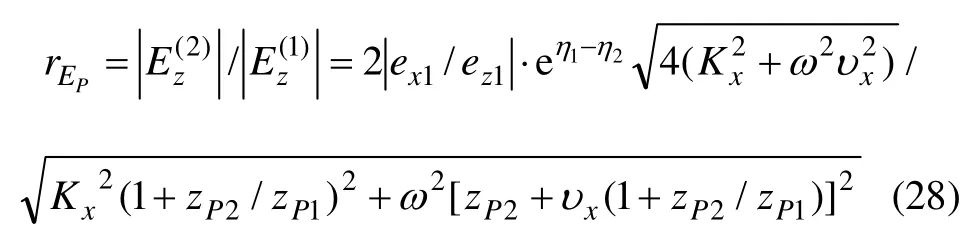
3.2.2 横波下电磁辐射强度变化
根据式(5),(7)和(19)可得到横波作用下电磁辐射在节理面前后的表达式:

将式(30)除以式(29)即得到节理面前后横波下电磁辐射的强度变化:
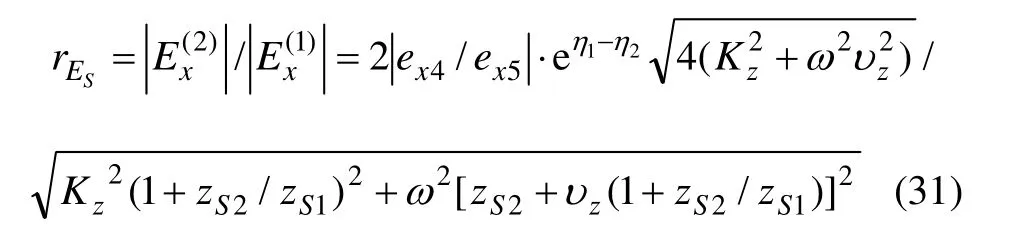
4 参数研究
主要研究节理初始刚度、节理面两侧岩体电性参数之比以及入射波频率 f 对电磁辐射强度变化的影响。取介质1岩石密度为2.7 t/m3,纵波传播速度为5.6 km/s, 则纵 波 波阻 抗 ZP1=ρ1vP1=1.51×107kg/(m2·s)。
对于节理面两侧岩体性质相同的情况,根据式(22),可得到电磁辐射强度rEp随频率和黏性系数的变化,分别如图1和图2所示。
对于节理面两侧岩体性质不同的情况,在式(28)中,对 6 mm晶系取压电系数 ex1=0.171,32晶系ez1=-0.051[12],zp2/zp1分别取 1.410和 0.707,电阻率ρ1=300 Ω·m,ρ2=500 Ω·m 时,电磁辐射强度的变化随节理的刚度和入射波的频率变化曲线分别如图3~4所示。由图1和图3可知,电磁辐射强度变化rEp随Kx0增大而增大,这表明具有较大初始刚度的节理能传递更多的波;rEp随频率的增大而减小,当含有多种频率成分的波入射到节理面时,高频成分比低频成分衰减要快。高频信号穿过岩石圈节理等发生快速衰减以至无法传播到地面被检测到,这也是人们普遍观测到地震低频和超低频电磁信号的重要原因。
由图 1还可以看出:rEp<1,说明岩体中的节理对电磁辐射的强度有衰减作用。作为地震时与电磁辐射的同步现象声发射,在强度上有类似的变化趋势。声发射在传播过程中会发生衰减,频率f越大,幅值越小;品质因子Q越小,衰减越大[15]。岩石中存在的节理是影响岩石品质因子的重要因素[16],声发射波通过宏观结构面产生透射损失,结构面越发育,实际岩体的Q越小,透射损失越大。这与本文理论分析结果相符。
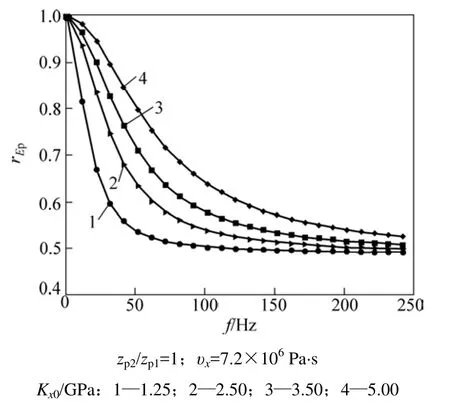
图1 节理间两侧介质性质相同时,刚度Kx0不同时,rEp随频率f的变化Fig.1 rEp variation with frequency under different Kx0 and same properties of rock on two sides of joint
图2 和4所示为不同频率下,电磁辐射强度变化rEp随黏性系数 υx的变化。从图2和4均可看出:强度变化 rEp随黏性系数υx的增加先减小然后增大;电磁辐射强度随黏性系数的变化同时受到频率的影响,随着频率的增大,强度下降量越来越大,而且强度最低点所对应的黏性系数越来越小,到达高频(105Hz)后,该黏性系数接近 0;越过强度最低点后,电磁辐射强度随黏性系数增大而增大。黏性是岩石流体特性的一种表现,张流等[17]在试验中发现,对于少量含水的岩石电阻率下降,随着含水量增多,岩石电阻率呈上升趋势,而电磁辐射强度是随电阻率增大而增大的,因此,电磁辐射强度随黏性系数先减小后增大。
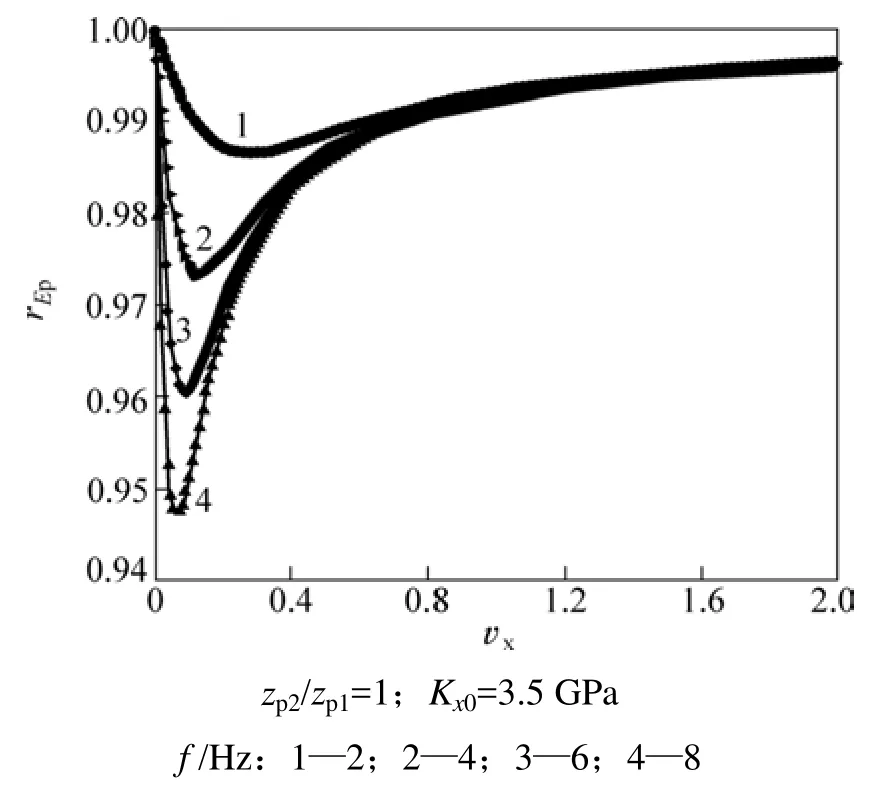
图2 节理间两侧介质性质相同、频率f不同时,rEp随黏性系数υx的变化Fig.2 rEp variation with υx under different frequency and same properties of rocks on two sides of joint

图3 节理间两侧介质性质不同、刚度Kx0不同时,rEp随频率f的变化Fig.3 rEp variation with frequency under different Kx0 and properties of rocks on two sides of joint
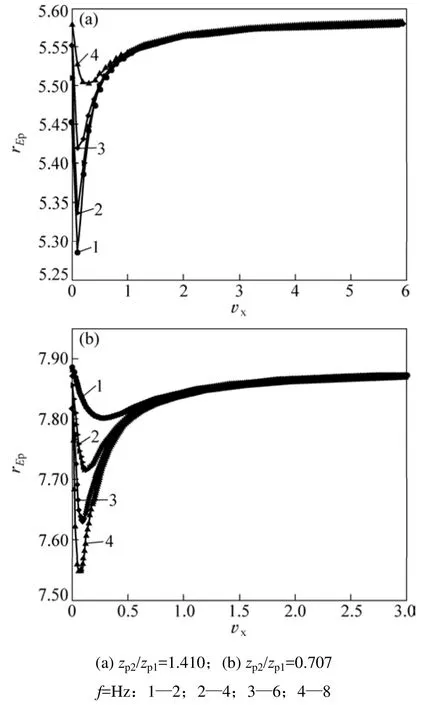
图4 节理间两侧介质性质不同、频率不同时,rEp随黏性系数υx变化Fig.4 rEp variation with υx under different frequency and properties of rocks on two sides of joint is different
与图1和2相比,图3和图4中电磁辐射强度更大,且大于 1,这并不意味着节理对电磁辐射没有衰减作用,而是在这种情况下,电磁辐射强度的变化除了受节理参数(如节理刚度、黏性系数)和入射波频率的影响外,同时还受到节理两侧岩体性质如波阻抗之比、压电系数之比以及岩体电阻率之比的共同影响。在图3和图4中,由介质1通过节理至介质2,压电系数和电阻率均增大,因为电磁辐射强度随电阻率和压电系数增大而增大,所以,电磁辐射强度增大。从理论上来讲,当其他参数保持不变时,由电阻率小的岩体通过节理面进入电阻率较大的岩体电磁辐射的强度会增大(即rEp>1);由压电系数小的岩体进入压电系数大的岩体电磁辐射的强度增大。但在多种参数的综合影响下,电磁辐射强度的变化更加复杂。
5 讨论
本文研究的前提是压电效应,但从岩石变形到破裂过程中,可能有多种产生电磁辐射的机制存在,除了有伴随微破裂同步出现的电磁辐射外,还有不伴随破裂出现的电磁辐射,因此,并不能排除其他电磁效应的存在。
值得说明的是:本文所考虑的是线性节理,纵横波透射解的表达式是完全相同的,对于横波,只是分别将节理法向刚度换成切向刚度,将纵波速度换成横波速度而已。因此,只给出了纵波下电磁辐射强度变化随各参数的变化,对于横波的情况,是完全类似的。另外,本文所考虑的是开尔文模型节理,所得结果也只适用于该类型节理。
6 结论
(1) 基于压电效应,依据应力波下电磁辐射与应力波之间的关系以及应力波在开尔文模型节理处的透射解,得到节理面前后的电磁辐射强度变化与节理参数之间的关系表达式。
(2) 入射波频率越高,电磁辐射强度衰减越严重;节理对电磁辐射的强度具有衰减作用,节理刚度越大,衰减越小。
(3) 电磁辐射强度随黏性系数先减小后增大,这与黏性系数变化过程中所导致的电阻率的变化相关;并且电磁辐射强度随黏性系数的变化受到频率的影响:随着频率的增大,强度下降量越来越大,强度最低点所对应的黏性系数越来越小,到达高频(105Hz)后,该黏性系数接近 0;越过强度最低点后,电磁辐射强度随黏性系数增大而增大。
(4) 对于节理面两侧岩体性质不同的情况,从理论上来说,电磁辐射强度随单个参数的变化是明确的,如由电阻率较小的岩体进入电阻率较大的岩体,电磁辐射的强度会增大,但电磁辐射强度的变化同时受到多种参数如节理参数(包括节理刚度、黏性系数)以及节理两侧岩体性质如波阻抗之比、压电系数之比和电阻率之比的影响,因此,电磁辐射的强度变化情况更加复杂。
[1] 郭自强, 周大庄, 施行觉, 等. 岩石破裂中的电子发射[J]. 地球物理学报, 1988, 31(5): 566-571.
GUO Zi-qiang, ZHOU Da-zhuang, SHI Xing-jue, et al. Electrons emission during rock fracture[J]. Chinese J Geophys (Acta Geophysica Sinica), 1988, 31(5): 566-571.
[2] 钱书清, 任克新, 吕智. 伴随岩石破裂的 VLF, MF, HF和VHF电磁辐射特性的实验研究[J]. 地震学报, 1996, 18(3):346-351.
QIAN Shu-qing, REN Ke-xin, LÜ Zhi. Experimental study of the feature of VL F, MF HF and VHF electromagnetic radiation accompanying rock fracture[J]. Acta Seismologica Sinica, 1996,18(3): 346-351.
[3] 刘煜洲, 刘因, 王寅生, 等. 岩石破裂时电磁辐射的影响因素和机理[J]. 地震学报, 1997, 19(4): 418-425.
LIU Yu-zhou, LIU-Yin, WANG Yin-sheng, et al. The influencing factors and mechanisms of the electromagnetic radiation during rock fracture[J]. Acta Seismologica Sinica, 1997,19(4): 418-425.
[4] Ogawa T, Utada H. Coseismic piezoelectric effects due to a dislocation 1. An analytic far and early-time field solution in a homogeneous whole space[J]. Phys Earth Planet Inter, 2000,121(3/4): 273-288.
[5] Gernets A A, Makarets M V, Koshevaya S V, et al.Electromagnetic emission caused by the fracturing of piezoelectric crystals with an arbitrarily oriented moving crack[J]. Phys Chem Earth, 2004, 29(4/9): 463-472.
[6] Warwick J W, Stoker C, Meyer T R. Radio emission associated with rock facture: Possible application to the great Chilean earthquake of May 22, 1960[J]. J Geophys Res, 1982, 87(B4):2851-2859.
[7] Huang Q. One possible generation mechanism of co-seismic electric signals[J]. Proc Japan Acad, 2002, 78(7): 173-178.
[8] Brady B T, Rowell G A. Laboratory investigation of the electrodynamics of rock fracture[J]. Nature, 1986, 321: 488-492.
[9] Makarets M V, Koshevaya S V, Gernets A A. Electromagnetic emission caused by the fracturing of piezoelectrics in the rocks[J]. Phys Scr, 2002, 65(3): 268-272.
[10] Koshevaya S, Makarets N, Grimalsky V, et al. Spectrum of the seismic-electromagnetic and acoustic waves caused by seismic and volcano activity[J]. Natural Hazards and Earth System Sciences, 2005, 5(2): 203-209.
[11] 万国香, 李夕兵. 应力波下节理面前后电磁辐射强度的变化[J]. 地震学报, 2009, 31(4): 411-423.
WAN Guo-xiang, LI Xi-bing. The intensity variation of the electromagnetic emission (EME) of rock masses with joint subjected to stress wave[J]. Acta Seismologica Sinica, 2009,31(4): 411-423.
[12] Auld B A. 固体中的声场和波[M]. 孙承平, 译. 北京: 科学出版社, 1982: 265.
Auld B A. Acoustic field and waves in solids[M]. SUN Cheng-ping, trans. Beijing: Science Press, 1982: 265.
[13] 肖红飞, 何学秋, 冯涛, 等. 基于 FLAC2D模拟的矿山巷道掘进煤岩变形破裂力电耦合规律研究[J]. 岩石力学与工程学报,2005, 24(13): 2304-2309.
XIAO Hong-fei, He Xue-qiu, Feng Tao, et al. Research on coupling laws between EME and stress fields during deformation and fracture of mine tunnel excavation based on FLAC2D[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(13): 2304-2309.
[14] Pyrak-Nolte L J. The seismic response of fractures and the interrelations among fracture properties[J]. Int J Rock Mech Min Sci, 1996, 33(8): 787-802.
[15] 胜山邦久. 声发射AE技术的应用[M]. 冯夏庭, 译. 北京: 冶金工业出版社, 1996: 52-54.
Katsuyama K. The application of acoustic emission technology[M]. FENG Xia-ting, trans. Beijing: Metallurgical Industry Press, 1996: 52-54.
[16] 李振生, 刘德良, 刘波, 等. 断层封闭性的波速和品质因子评价方法[J]. 科学通报, 2005, 50(13): 1365-1369.
LI Zhen-sheng, LIU De-liang, LIU Bo, et al. The evaluation method of wave velocity and quality factor of Fault Seal Property[J]. Chinese Science Bulletin, 2005, 50(13): 1365-1369.
[17] 张流, 黄建国, 高平. 水对岩石变形过程中电阻率变化的影响[J]. 地震, 2003, 23(1): 8-14.
ZHANG Liu, HUANG Jian-guo, GAO Ping. Influence of water on electric resistivity of deforming rock samples[J]. Earthquake,2003, 23(1): 8-14.
