重力坝沿建基面抗滑稳定的研究
2011-05-31杨清平李俊杰
杨清平 ,李俊杰
(大连理工大学,辽宁 大连 116023)
抗滑稳定分析是重力坝设计中的一项重要内容,其目的是核算坝体沿建基面或地基深层软弱结构面抗滑稳定的安全度。各国的规范都规定在岩基上进行重力坝设计时必须审查大坝沿坝建基面的抗滑稳定问题。我国《混凝土重力坝设计规范》建议给出了沿建基面抗滑稳定分析的抗剪强度公式和抗剪断公式,并给出了相应的安全系数。但抗剪强度公式和抗剪断公式都是对重力坝进行整体抗滑稳定分析,整体抗滑稳定分析不能反应重力坝剪切失稳的实际过程。所以,采用反应局部效应的点安全系数法来分析重力坝失稳的过程。另外,重力坝沿坝轴线方向用横缝分成独立工作的若干坝段,所以,稳定问题可以按平面问题分析。由于影响抗滑稳定的因素很多,例如基岩特性、地基破碎层、地基软弱夹层、坝体材料分区、地基与坝体弹模比、扬压力等,所以迄今为止,没有成型的公认的理论来分析抗滑稳定,因此,有必要做工作来分析重力坝的抗滑稳定问题。
1 计算工况和网格剖分
文中分别以 80,110,160,190 m 高的重力坝作为研究对象,上游坝坡垂直,下游坝坡为1∶0.75,考虑坝体自重和上游水压力,下游无水。其典型断面和计算水位如图1所示。
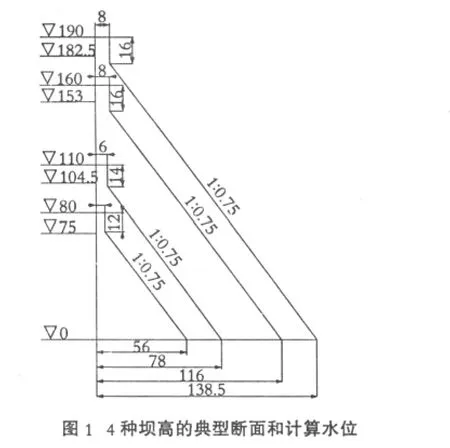
2 点的安全系数
重力坝的抗滑稳定破坏准则[1]分为三种:点破坏准则,整体破坏准则,极限破坏准则。由于用整体破坏准则来研究重力坝的抗滑稳定问题太过于笼统,并不能满足点的破坏准则和反应发生剪切屈服而产生的局部破坏,因此用整体破坏准则研究抗滑稳定问题需要较大的安全余度。文中用点的破坏准则来研究重力坝的抗滑稳定问题。
假设岩体的抗剪强度为τf,根据库仑--奈维尔准则:

假设某单元的任意一截面的剪应力τ,当τ<τf则不会发生剪切破坏;τ=τf时,则达到临界状态;当τ>τf时,则发生剪切破坏。

Kp的最小值称为点的最小安全系数,用Kpmin表示。

从图2中可以看出:
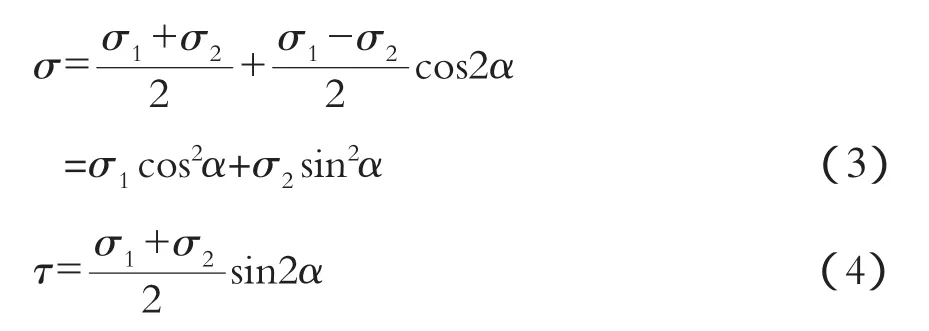
使σ保持不变,τ达到τf时发生剪切破坏。此时:

求得:
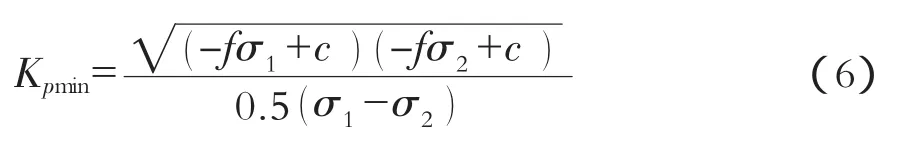
破坏角α0可以由下式求得:

3 材料强度储备系数Kf
给建基面的抗剪断摩擦系数和凝聚力一定的安全储备,即把抗剪断摩擦系数和凝聚力除以一定的常数Kf,用式表示为:

即用提高Kf值的办法来近似描述坝基的渐进破坏过程。此时的Kpmin为:
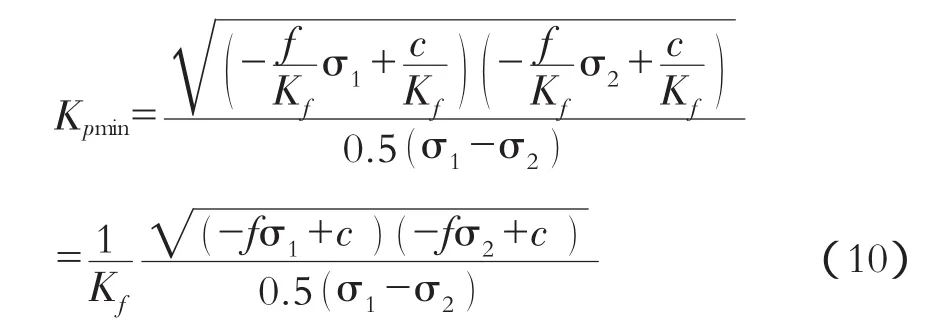
4 材料参数
坝体和坝基均采用线弹性模型,并认为坝基是均匀的,坝体弹模为Ed=19.6×109Pa。基岩变形模量分别为 Ef=39.2×109,19.6×109,9.8×109Pa。把变形模量、建基面抗剪断摩擦系数和凝聚力列于表1中。
本文运用Abaqus有限元软件建立了施工段三维计算模型,并对盾构施工过程进行精细化仿真模拟。模拟中,假定工程条件及仿真方法如下:

表1 计算时建基面采用的抗剪断参数
5 沿建基面的剪应力τxy分布规律
为了研究方便,引入坝踵沿建基面相对宽度的概念,定义坝踵相对宽度brl为沿建基面距坝踵的距离b与坝体底宽B的比值,用公式表示为brl=b/B×100%。
由于计算工况很多,在此计算结果不能一一列出,文中选取110坝地基与坝体弹模比为1.0时的剪应力分布绘于图3中。从图3中可以看出,剪应力在坝趾处为其最大值,沿建基面向上游剪应力逐渐减小,在距坝踵较近处达到其最小值。

把不同地基与坝体弹模比情况下的剪应力分布绘于图4中。从图4可以看出:
1)地基弹模越小,在坝趾处有较大的剪应力,在靠近坝踵的部分,几种弹模比情况下的剪应力差异不大。
2)在距坝踵相对宽度大约为0.78的地方,几种弹模比情况下,坝体沿建基面在该处具有相同的剪应力值。
3)从总体上说,坝基弹模越大,剪应力沿建基面的分布越均匀。地基弹模越小,剪应力沿建基面的分布有较大的梯度。

6 点安全系数沿建基面的分布
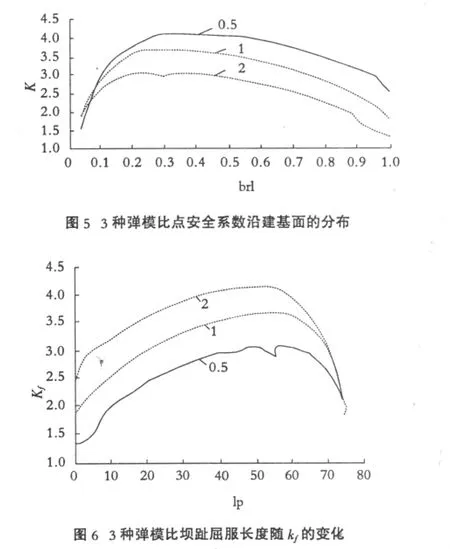
选110 m坝,3种弹模比情况下计算得到的点安全系数绘于图5中。由于在坝踵处计算的到的垂直向应力是不准确的,因此,此处的点安全系数分布是不准确的,在此不作详细探讨。从图5中可以看出:
1)无论在什么弹模比情况下,坝趾区都有较小的点安全系数,沿建基面由坝趾向坝踵点安全系数逐渐增加,坝趾区应先发生剪切屈服。
2)在距坝趾较近的地方点安全系数的梯度很大,在建基面距坝趾较远处,点安全系数的变化相对平缓。
3)在几种弹模比的情况下,地基弹模较小时,沿建基面有较小的点安全系数的分布,随着弹模比的增大,即地基弹模的增大,点安全系数发生平行增大,因此,地基弹模越小,坝趾发生剪切屈服的时间越早。
7 用强度储备系数法研究重力坝的抗滑稳定
前面的计算分析是基于弹性理论的结果,并未考虑重力坝的剪切破坏。为了进一步研究重力坝沿剪基面的剪切破坏规律,用提升强度储备系数的方法来研究重力坝沿剪基面的剪切破坏,破坏准则采用摩尔-库仑准则[2]。
通过对4种坝高进行了反复迭代计算,把110 m坝在3种弹模比情况下的坝趾屈服区长度,随强度储备系数的变化绘于图6中,从6中可以看出:
1)随着强度储备系数的提高,坝趾区首先发生剪切屈服。
2)在距坝趾较近的区域内,随着强度储备系数的提高,坝趾的剪切屈服向上游拓展。
3)当屈服区拓展到一定长度时,随着强度储备系数的提高,坝趾区的剪切屈服长度变化不大。
4)当强度储备系数的提高到一定值时,剪切屈服区迅速拓展,直至整个建基面发生剪切屈服。
[1]潘家铮.重力坝设计[M].北京:水利电力出版社,1987.
[2]龚晓南.土塑性力学[M].杭州:浙江大学出版社,1990.
