人脸轮廓信息的提取

原 瑾

（山西广播电视卫星地球站，太原 030021）

1 引言

边缘特征提取是图像处理、计算机视觉中最基础的内容，并在应用中起着重要的作用，它是图像分析与识别重要的环节，是进行目标检测、图像分割所依赖的重要特征。

在图像处理上，可以粗略地分为阶跃边缘（Stepedge）和屋顶边缘（Roofedge）两种。经典的微分边缘检测算子利用边缘处的一阶导数最大或最小，阶跃边缘点处二阶导数呈零交叉或屋顶边缘点处二阶方向导数取极值等。近年来，随着数学和人工智能的发展，出现了一些新的边缘检测方法，如数学形态法、小波变换法、神经网络法、模糊检测法等等。这些算法都在力图最大程度地抑制噪声和多尺度地探测特征边缘。最近的二十年里发展了许多边缘检测器，常用的几种边缘检测器包括Roberts算子、Sobel算子、Prewitt算子、拉普拉斯算子、二阶方向导数、LOG算子等。各种边缘检测效果如图1。

在本文中，主要采用Kirsch算子，并基于阶跃性边缘提出了一种动态阈值自动获取法，它是根据图像本身特点及Kirsh值的取值情况自动调整阈值，以获得图像最可能的边缘点。利用该方法并采用matlab编程实验证明，图像信息能够得到较好的提取。

图1 各种边缘检测效果

2 Kirsch算子

这是一个3×3的非线性算子，其基本思想是先使边缘两侧的像素各自与同类的像素取平均值，以改进求平均值的过程，然后求平均值之差，以减少由于平均造成的边缘细节丢失。

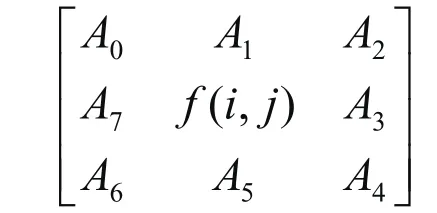
Kirsch算法中的边缘算子有8个卷积组成，每个小区域分别代表一种特定的检测方向。如图2所示，图像中的每个点都用8个掩模进行卷积，每个掩模都对某个特定边缘方向作出最大响应。所有8个方向中的最大值作为边缘幅度图像的输出。最大响应掩模的序号构成了边缘方向的编码。

图2 Kirsch边缘算子

具体方法是，在进行边缘检测时，把图2所表示的边缘模板（加权矩阵）分别与图像中的一个3×3区域相乘。选取输出值为最大的模板，假设图像中某一像素点A及其周围领域3×3区域的灰度模板，如图3所示。

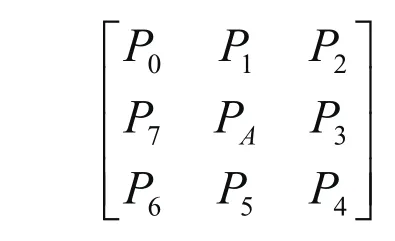
图3 窗口设置示意图

设gi（i=0，1……7）为图像经过Kirsch算子第i+1个模板处理后得到的A点的灰度值。例如，经过第一个窗口模板处理后A点灰度值为：

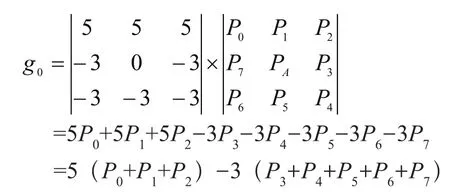
经过8个窗口模板处理后，在A点的灰度值为：

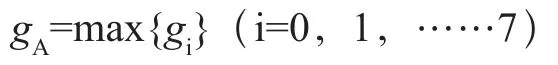
边缘方向为最大灰度值所代表的方向，如图4。

图4 边缘方向

3 边缘提取的动态阈值获取

人脸图像中包含了大量的有用信息，例如人的五官，基于此可以进行人脸识别，同时，图像中还含有大量的无用信息，如背景图像，这样就造成了图像信息处理资源的浪费。因此，有必要先对图片进行初步处理，提取出人脸图像的轮廓信息，进行初步定位，这样可以提高数字图像的处理速度，节约系统资源。

物体的边缘是由灰度的不连续性反映出来的，边缘提取的经典方法是针对图像的每个像素的某个领域内灰度的变化是否超过某一阈值来确定该像素点是否是边缘点。根据阶跃性边缘还是屋顶状边缘，可以分别用一阶方向导数或二阶方向导数的变化情况进行边缘检测。从简单性和效果两方面考虑，我们选择了Kitsch边缘检测方法。Kirsch直接针对像素的八个邻点的灰度变化情况提出Kirsch算子，这种方法直观且容易实现。

需要强调的是，这里所指的是合理控制成本，而非一味地追求低廉成本。合理控制成本就是在满足用户功能需求的前提下，要找到产品最佳的性价比。高技术全智能小型专项农具是理想化的解决方案，但其高昂的价格是很难被使用者接受的。另外，在设计伊始就要全面考虑产品寿命周期费用，产品的使用费用、维修保养费用都将直接影响用户的接受程度。所以，结实耐用和易于维修保养是小型专项农具设计的又一目标。

Kirsch算子的基本思想是这样的：对数字图像的每个像素I，考虑它的八个邻点的灰度值，以其中三个相邻点的加权和减去剩下五个邻点的加权和得到的差值，令三个邻点绕该像素点不断移位。取此八个差值的最大值作为Kirsch算子。

设Si为三邻点之和，Ti为五邻点之和，则Kirsch算子定义为：

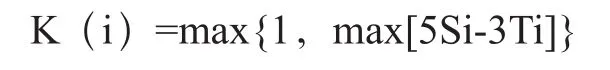
如取阈值THk，则K（i）＞THk时，像素I为阶跃边缘点。对于大图像库，提取库中所有图像的边缘是一个艰巨的任务。由于每个图像都有自己特定的目标和背景，必然不可能有固定的阈值。如果用Kirsch算子，将阈值定为某一适当值，则对于有些图像很可能将某些假边缘也提取出来，而有些目标和背景之间灰度变化较小的图像则取不到目标边缘。因此，我们希望找到一种简单的方法，阈值能够随图像的变化自动调整，使各种图像的边缘均能很好地被取出。下面基于阶跃性边缘提出了一种动态阈值自动获取法，它是根据图像本身特点及Kirsch值的取值情况自动调整阈值，以获得图像的最可能的边缘点。

4 图像边缘的特性分析

为适应图像识别或图像检索，将图像分为场景图、目标图和纹理图。场景图是指以背景（风景或零乱的小物体组合等）为画面的主要部分，没有明显目标的图像；目标图是指具有明显目标的图像，物体可以存在于场景之中，也可以是多目标；纹理图是指局部不规则而宏观有规律的纹理特性为主导的图像。如果对场景图作边缘提取，得到的边缘点呈现出分散及零乱的不规则性。而对纹理图作边缘提取，边缘点呈不连续及一定的规律性，这种特性使得计算机能够将场景图和纹理图从一个图像库中区别出来，而剩下目标图。目标图的边缘有明显的连续性和一定的集中性，为边缘阈值的自动提取提供了一定的可行性。

一幅任意大小的图像，如果是目标图，其边缘像素点相对图像大小来说是很有限的。用某种确定的方法和一定的阈值作边缘提取后，如果取出的边缘像素点很多，显然其阈值定得不准确。阈值太低会使许多不是边缘点的像素也被提取出来，致使得到的边缘像素很多；但阈值太高又会使灰度变化小的图像的边缘点取不到，为能适合大图像库中全部图像的边缘自动提取，需要用动态阈值法来自动调整阈值。

5 阈值的动态调整

假设图像大小为H×W个像素点，其边缘点像素一般不会超过H×W/5个，对于具有一定目标的图像，这是个比较宽松的限定值。我们用Kirsch算法，取某一较低的初始阈值THk（以保证目标和背景间灰度变化很小的图像边缘也能被取出），对于每个像素点i 计算其Kirsch算子，如果K（i）＞THk，则i为边缘点，边缘点数N（初始值为0）加1，一旦边缘点数超过5×H，而i还小于整幅图像的像素数，说明阈值取得太低，致使许多不是边缘点的像素也被取出,因此需提高阈值。

为适合大图像库中所有图像边缘提取的需要，THk的初始值定得较低，这样虽然保证了目标和背景间灰度变化很小的图像边缘点也能被取出，但在某些图像中可能初始THk值与真正的边缘阈值相差的很远，因此需记录满足K（i）＞THk条件的最小的K（i），记作Kmin，这个最小值可能远远大于初始阈值，将次最小值作为调整的基础，当 n≥5×H时取THk=Kmin，这样第一步就可以将阈值调整到合适的位置，以后一旦边缘点数N超过预定值，则取调整后得到的Kmin作为新的阈值THk， 因此，每次阈值调整去掉的是最小值，这样就不致错过任何可能的边缘。整个过程按如下方法逐步调整：

（1）如果K（i）＞THk，则 i 为边缘点，记录边缘点 i 的坐标及K（i）的最小值Kmin=min{K（i）}，同时N加1；

（2）一旦n≥5×H， 则将阈值调整到满足最低边缘要求最小值处，即取THk=Kmin；

（3）将前面已得到的边缘点和新的阈值作比较，取大于新阈值的点为新的边缘点。并重新计算此新阈值下的Kmin， 记录新边缘点的newn；

（4）将新的边缘点数赋给n， 后面的计数从n=newn开始；

（5）继续对剩下的部分图像进行第（1）步的处理， 如n≥5×H，则又回到第（2）步，否则结束该图像的边缘提取。

这样图像库中所有图像的边缘提取均能自动完成，而不需人工干预。

该方法实现了阈值的自动调整。但是，在初步设定阈值时，只是人为设定了一个数值，而不是针对图像的具体像素点来由计算机自动设定阈值。我们对这一问题进行了改进，由计算机根据图像各个像素点灰度值的平均值来自动调整初步阈值，这样可以使程序更快地调整到恰当的阈值位置，并且不错过每一个可能的边缘点。然后将得到图像灰度值的平均值作为图像的阈值，再对图像进行处理，就可以达到预期的效果，使阈值尽可能最快地达到最佳值，以减少程序的运算时间。

程序流程图如图6。

图5 Kirsch算子处理前后对比图

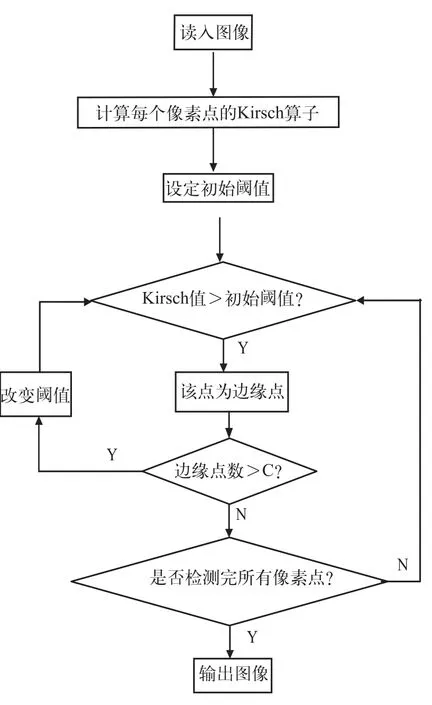
图6 程序流程图

基于Kirsch的动态阈值的边缘提取方法是一种比较理想的方法，使图像信息能够得到较好的提取，在目前图像边缘提取方法中属于比较完善的方法，具有相当的可行性。

6 结论

图像处理和计算机视觉都是新兴学科，近几十年来，随着研究的深入和应用的需要，新概念、新思想、新方法陆续产生，它们正朝着智能化、系统化的方向发展。而作为图像处理和计算机视觉领域最基本的技术之一的图像边缘提取技术，也已突破其狭义的概念，成为一个内容丰富的领域。

本文中研究了各种算子，致力于找到一种最好的算法，使得提取效果达到最佳。边缘检测作为数字图像处理的一个重要内容一直是人们研究的热点。在实际应用中有许多成功的例子，已将一些专用领域的成熟算法嵌入单片机，制成便携式设备，如指纹考勤机、人脸识别器等，但这些算法都有一定的局限性，所谓“好”的算法是相对于某一类图像而言的，通用性差。因此，提高算法的通用性，已成为新的研究方向。

[1] 冈萨雷斯.数字图像处理（英文版）[M].北京：电子工业出版社，2004.

[2] 王良民，张建明，詹永照，等.人脸检测研究现状和发展[J].江苏大学学报（自然科学版），2003，24（3）：75-79.

[3] 张兆礼，赵春晖，等.现代图像处理技术及MATLAB实现[M]. 北京：人民邮电出版社，2001.

[4] 章毓晋.图像分割[M]. 北京：科学出版社，2001.

[5] 章毓晋.图像处理和分析[M]. 北京：清华大学出版社，1999.