柱面共形阵列天线盲极化波达方向估计算法
2011-05-29齐子森王布宏姚战宏
齐子森 郭 英 王布宏 姚战宏
(1.空军工程大学电讯工程学院,陕西 西安 710077; 2.空军工程大学电子信息系统综合集成重点实验室,陕西 西安 710051)
1.引 言
“灵巧蒙皮”的共形阵列天线[1]在未来舰载、弹载雷达以及航天飞行器的天线设计中具有广泛的应用前景,已成为未来天线的发展方向。对共形阵列天线高速、高精度信源方位估计技术的研究具有重要的现实意义。利用共形阵列天线实现信源方位估计必须考虑阵列流形多极化特性(polarization diversity)[2-4]的影响,即共形天线的流形建模必须考虑单元方向图的影响,共形阵列天线的方位估计需要与信源极化状态联合进行[5-7]。因此许多适用于经典阵列(线阵、面阵)的波达方向(DOA)估计方法在共形阵列天线中无法简单移植应用。基于多维搜索的算法因极化参数的引入,使得计算量急剧增加,工程实现不可接受。
对共形阵列天线DOA估计方法的研究已取得一定成果[5-13],但多数已有文献[8]-[13]都压缩了待估参数空间,假设了不现实的前提条件,简化了共形阵列天线的流形模型。完全考虑共形天线多极化的流形特点进行方位估计的研究报道并不多见[5-7]。文献[2]-[4]完整构建了共形天线阵列流形的数学模型,给出了共形天线阵列流形建模的统一方法,为全面考虑共形阵列天线特点的信号处理研究奠定了基础。文献[5]在假设信源极化状态已知条件下,详细分析了多重信号分类法(MUSIC)[14]算法在不同阵列形式(锥面、柱面以及球面)中的DOA估计性能。文献[6]-[7]针对锥面共形载体,通过合理的阵元设置,结合旋转不变子空间算法(ESPRIT,estimation of signal parameters via rotational invariance techniques)[15]参数估计的特殊要求,提出了锥面共形阵列天线盲极化DOA估计算法。该算法通过将信源极化参数与方位参数去耦合,实现了锥面共形阵列天线的高分辨DOA估计。但是该算法利用了锥面共形载体的单曲率特性以及锥面母线间的不同夹角,其仅适用于锥面共形阵列,不能解决其他共形载体的信源方位估计问题。柱面共形载体是构成大多数飞行器的基本结构,具有广泛的应用环境,是最为常见的共形载体之一。柱面共形载体亦具有单曲率特性,但其母线夹角为零的特点使得上述盲极化DOA估计算法不再适用。可见,对共形阵列天线高分辨DOA估计技术的研究很不充分,探讨其他共形结构阵列的高分辨DOA估计方法是迫切而有必要的。
基于此,本文针对柱面共形阵列天线的单曲率特点,在给出柱面共形阵列天线窄带数据模型的基础上,通过合理的阵元排列结构,结合DOA估计的子空间原理[14]与秩损理论[16-17],实现了信源方位角、俯仰角以及极化状态的去耦合,提出了独立信源条件下的柱面共形阵列天线盲极化DOA估计方法。该方法无需参数配对,通过参数的一维搜索,可实现信源方位估计,计算量小,阵元利用率高。针对相干信源情况,推导了柱面共形阵列天线的解相干算法,在此基础上实现了柱面共形阵列天线相干信源的盲极化DOA估计。最后,通过计算机Monte-Carlo仿真实验验证了所提算法的有效性。
2.柱面共形阵列天线窄带数据模型
我们前期工作[6-7]已详细论述了利用阵列分割克服共形载体遮蔽效应的原理。借鉴其阵列分割思想,将柱面共形阵列天线(全局坐标系为X′Y′Z′,坐标原点为o′,子阵坐标系为XYZ,坐标原点为o,如图1(a)所示)划分为多个结构相同的子阵,每个子阵列负责估计的方位角范围为α(如图1(b)所示,α=2arccos([abs(ΔP1)/2/d]),d表示半径,arccos(·)表示求(·)的反余弦,abs(·)为求(·)的模),在信源方位未知情况下,各子阵仅负责所属方位角范围内的信源方位估计,最终通过综合各子阵估计结果得到所有信源的方位估计[6-7]。由于柱面结构上的对称性,各子阵结构相同,因而,每一子阵DOA估计算法也相同,所以,仅对其中一个子阵进行算法详述和仿真。图1中,同一圆柱横截面上的两阵元间隔为λ/4,相邻横截面之间的间隔为λ/4(对于独立信源间隔可以不相等,此处设置为相同间隔来完成柱面共形阵列天线对相干信源的解相干预处理),横截面半径为d(单位为λ),λ为信号波长。
对于图1所示的柱面共形阵列天线子阵,建立如图1(a)所示的坐标系XYZ,则其窄带快拍数据模型可表示为式(1)~(16)。

(a) 柱面共形载体上的阵元结构
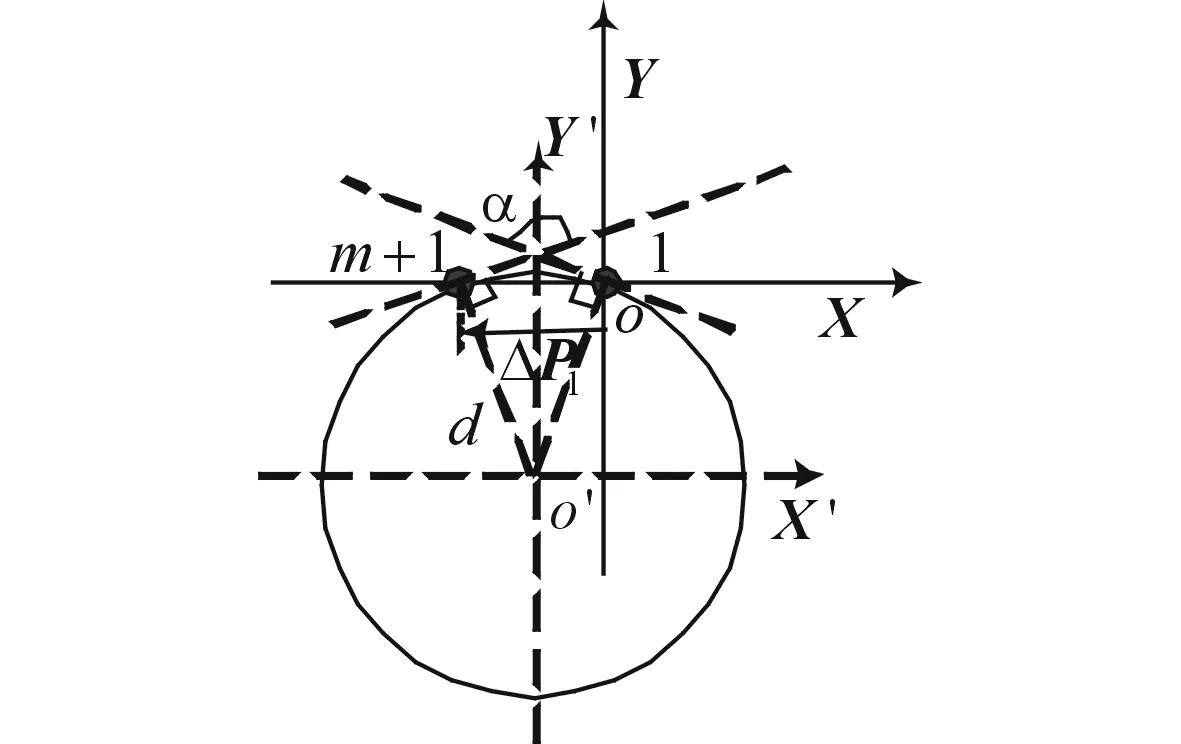
(b) 柱面共形阵列俯视图

(c) 信源方向矢量u图1 柱面共形阵列天线
(1)
u= sinθcosφX+sinθsinφY+cosθZ
(2)
=|gi||pl|cosθigk
=gi·pl
=gi θkθ+gi φkφ
(3)
gi=gi θ(θ,φ)uθ+gi φ(θ,φ)uφ
(4)
pl=kθuθ+kφuφ
(5)
uθ= cosθcosφX+cosθsinφY-sinθZ
(6)
uφ=-sinφX+cosφY
(7)
(·)1·(·)2表示两矢量(·)1与(·)2的点乘运算;ri表示共形阵列天线中第i个阵元在全局坐标系中对单位强度入射信号的响应[6];gi表示第i个阵元的单元方向图;giθ,giφ为第i个阵元单元方向图在基矢量上的分量;kθ,kφ表示入射信号极化状态,即入射信号电场矢量pl在基矢量上的分量;θigk为gi与pl的夹角;pi为第i个阵元位置与坐标原点构成的矢量;2m为阵元个数;(·)T表示取(·)的转置。
当信源个数为n时,窄带数据模型为
X=AS+N=(AθKθ+AφKφ)S+N
(8)
S=[s1,s2,…,sn]T
(9)
N=[n1,n2,…,nn]T
(10)
Aθ=[aθ(θ1,φ1),aθ(θ2,φ2),…,aθ(θn,φn)]
(11)
Aφ=[aφ(θ1,φ1),aφ(θ2,φ2),…,aφ(θn,φn)]
(12)
Kθ=diag(k1θ,k2θ,…,knθ)
(13)
Kφ=diag(k1φ,k2φ,…,knφ)
(14)
式中:A为流形矩阵;S为信号矢量;N为噪声矢量;n为信源个数;K=diag(k1,k2,…,kn)表示矩阵K为以k1,k2,…,kn为主对角线元素构成的对角阵;θi,φi表示第i个入射信号在全局坐标系中的俯仰角与方位角;kiθ,kiθ分别为第i个入射信号极化矢量在uθ,uφ上的分量。当空间存在相干信源时,所谓相干是指信源之间差一个复常数,即
si=βis0
(15)
若n个信源均为相干信源,则信号矢量S为
S=[β1,β2,…,βn]Ts0
(16)
综上可发现,共形阵列天线的快拍数据建模必需考虑天线单元方向图的影响,所以共形天线快拍数据建模时必需完成单元方向图在局部坐标系到全局坐标系的旋转变换[2-4],因此共形天线的阵列流形具有了多极化特性。
3.独立信源盲极化DOA估计算法
共形阵列天线信源方位估计是多参数估计问题,由于导向矢量的精确建模需要已知信源极化状态的表征参数,从而增加了参数维数,使基于多维搜索DOA估计算法的计算量骤然增加。充分利用矩阵的特征向量与特征值进行多参数去耦并联合估计[16-18]可有效的减小计算量。基于此思想,本文利用柱面共形载体的单曲率特点,结合特殊的阵元排列结构,将信源俯仰角、方位角以及极化状态参数去耦合,通过一维搜索实现了盲极化柱面共形阵列天线的DOA估计,减小了计算量,保证了阵元的利用率(可估计最大信源数仅比阵元数小2,即nmax=2m-2)。
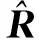
(17)

由共形载体的单曲率特性可知,处于同一母线上的天线单元具有相同的指向,此时有
r1=r2=…=rm
(18)
rm+1=rm+2=…=r2m
(19)
将式(18)、(19)代入式(1),可得
=QB
(20)
(21)
(22)
(23)
(24)
式中:0m×1为m×1阶的零矩阵; ΔP如图1(b)所示。由子空间原理[13]可知,导向矢量属于信号子空间,与噪声子空间正交,由于噪声影响,式(25)近似为零,即
=0
(25)
(26)
因为B各元素不为零,所以如果式(25)成立,则有矩阵Z奇异或出现秩损现象,只有在真实信源方位时,矩阵Z奇异[16-17]。且由于Pi,i=1,2,…,m仅在坐标轴Z上有分量,所以式(23)由信源俯仰角确定。基于此原理,信源俯仰角可通过最大化式(27)获得。
(27)

(28)
此时有

(29)

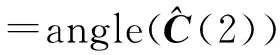
(30)
angle(·)表示求复数(·)的相角。所以有
(31)
因为
ΔP=sinθΔPcosφΔPX
(32)
又因为|ΔP|=λ/4,且θΔP=π/2,φΔP=π,结合式(2)、式(31)以及式(32),则有
(33)
所以,柱面共形阵列天线独立信源盲极化DOA估计算法步骤如下:

3) 对式(21)~(24)构造矩阵Q,B;
4) 将式(27)所示谱估计器的n个最高峰值对应的空间方位作为信源俯仰角估计值;
5) 结合式(29)与式(33)以及4)中获得的俯仰角估计值,求得信源方位角的估计值,从而实现信源方位估计。
4.相干信源盲极化DOA估计算法
相干信源使得信源协方差矩阵的秩小于信源个数,相应的通过特征值分解获得的信号子空间的维数亦小于信源个数,这就使得阵列流形矩阵张成的信号子空间与特征值分解获得的信号子空间不一致,从而导致基于特征值分解的高分辨DOA估计算法在空间存在相干信源时无法准确估计信源方位。空间平滑算法[19-20]是一种常用的解相干预处理算法,它利用均匀线阵的平移不变性,将均匀线阵划分为相互重叠的L个子阵,对应的每个子阵阵元个数为q,分别计算各子阵的自协方差矩阵,然后进行算术平均,从而得到一个等效的q阶子阵列的协方差矩阵。在均匀线阵中,当子阵阵元个数q大于信源个数时,经过空间平滑所得的q阶阵列协方差矩阵对应的信源协方差矩阵的秩恢复为信源数[18]。然而空间平滑算法对阵列的特殊要求限制了它的应用范围。在共形阵列天线中,阵列的均匀线阵结构一般不被满足,且由于共形载体曲率影响,天线单元方向图指向不一致,此时不可简单假设天线单元为全向单元。因此,在共形阵列天线中应用空间平滑算法面临巨大的困难。本文所述算法基于协方差矩阵特征值分解的子空间划分,为了适用于空间存在相干信源的情况,需要解相干预处理。
在图1所示阵列中,选取阵元1~q/2与阵元m+1~m+q/2构成子阵列h10,q为偶数;选取阵元2~q/2+1与阵元m+2~m+q/2+1构成子阵列h11;同理可得子阵h12,h13,…,h1L-1.子阵h1L-1由阵元L~q/2+L-1与阵元m+L~m+q/2+L-1构成,且q/2+L-1≤m,m+q/2+L-1≤2m,即保证阵元1~q/2+L-1与阵元m+1~m+q/2+L-1分别在两条母线上。由此可发现,阵列h10,h11,…,h1L-1虽不是均匀线阵,但具有相同的空间结构,子阵间距离矢量满足空间平滑算法的要求,且与单元方向图无关,此时可将空间平滑思想引入。各子阵接收相干信源数据为
Xh1i=Ah1iS+Nh1i
(34)
Ah1i= [ah1i(θ1,φ1),ah1i(θ2,φ2),…,
ah1i(θn,φn)]
(35)
(36)
式中,S如式(16)所示。由图1(a)结合各子阵阵元位置,可得
(37)
Ah1i=Ah10Di-1
(38)
(39)
各子阵的协方差矩阵为

(40)
式中,Ah1i表示阵列h1i所对应的流形矩阵。将L个子阵所得协方差矩阵做算数平均,有
(41)
将式(40)带入式(41),得
(42)
所以有
(43)
(44)
在完成解相干预处理的基础上,结合柱面共形阵列天线独立信源盲极化DOA估计算法,可实现柱面共形阵列天线相干信源盲极化DOA估计。算法步骤如下:
3) 将阵元个数2m换为2q(且2q>n),即在阵列h10上应用独立信源条件下的盲极化DOA估计算法,实现信源方位估计,最终完成柱面共形阵列天线相干信源的盲极化信源方位估计。
5.仿真实验
上述各节推导了算法机理,并给出了算法步骤,本节在此基础上进行Monte-Carlo仿真实验验证算法的有效性。其中,对成功实验的定义为:估计偏差小于2°的试验为成功实验。成功概率的定义为:成功试验次数与试验次数的比值。估计偏差定义为:在成功实验中,估计均值与真值之差的绝对值。估计标准差定义为:在成功实验中,估计值与估计均值之差的均方值开方。在此前提条件下,进行200次独立仿真实验。
仿真实验一
阵列结构如图1;快拍数N=100;信噪比SNR∈[5,30];信源个数n=2,且相互独立;阵列阵元个数为32,即m=16,柱面横截面半径d=5λ;在全局坐标系中θ1=85°,φ1=70°;θ2=90°,φ2=75°;k1θ=0.3,k1φ=0.7;k2θ=0.8,k2φ=0.2.单元方向图为
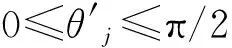
(45)


(46)

(47)
(48)


(a) 成功概率与信噪比的关系

(b) 估计偏差与信噪比的关系

(c) 估计标准差与信噪比的关系图2 100次快拍的独立信源盲极化DOA估计
仿真实验二
阵列阵元个数为34,即m=17;快拍数N=200;q=18;L=9;信源为相干信源,信源个数n=2,其他条件与仿真实验一相同。仿真结果如图3所示。由仿真结果可知,对相干信源方位的估计成功概率、估计偏差以及估计标准差都随着信噪比与阵元个数的增加而逐渐变好,达到了令人满意的效果。充分验证了算法对相干信源估计的有效性(如图3所示)。

(a) 成功概率与信噪比的关系

(b) 估计偏差与信噪比的关系
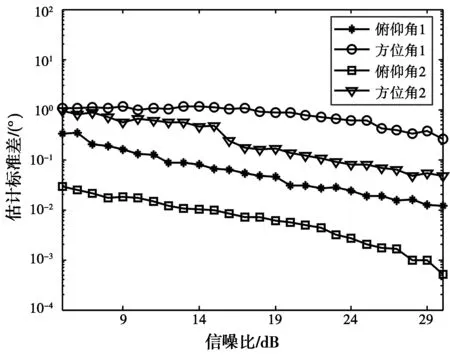
(c) 估计标准差与信噪比的关系图3 200次快拍的相干信源盲极化DOA估计
6.结 论
针对共形阵列天线中DOA估计需与信源极化状态联合进行的难题,论文利用柱面共形阵列天线的单曲率特点结合子空间原理,提出了柱面共形阵列天线盲极化DOA估计算法。详细推导了算法机理,给出了算法步骤。在此基础上针对相干信源方位估计问题,通过合理的阵元选取,讨论了柱面共形阵列天线的解相干预处理算法,从而实现了信源极化状态未知条件下相干信源的高分辨方位估计。计算机Monte-Carlo仿真实验表明,所提算法可以很好地解决柱面共形阵列天线盲极化条件下独立和相干信源的方位估计问题,从而验证了所提算法的有效性。
[1] JOSEFSSON L, PERSSON P. Conformal array antenna theory and design[M]. Canada: Wiley-IEEE Press, 2006.
[2] WANG Buhong, GUO Ying and WANG Yongliang. Frequency-invariant pattern synthesis of conformal array with low cross-polarization[J]. IET Microwaves, Antennas & Propagation, 2008, 2(5): 442-450.
[3] WANG Buhong, GUO Ying. Array manifold modeling for arbitrary 3D conformal array antenna[C]//Proceedings of 2008 IEEE International Workshop on Antenna Technology. Chiba, Japan, 2008: 562-565.
[4] 王布宏, 郭 英, 王永良. 共形天线阵列流形的建模方法[J]. 电子学报, 2009, 37(3): 481-484.
WANG Buhong, GUO Ying, WANG Yongliang. Array manifold modeling for conformal array antenna[J]. Acta Electronica Sinica, 2009, 37(3): 481-484. (in Chinese)
[5] 齐子森, 郭 英, 王布宏. 共形阵列天线MUSIC算法性能分析[J]. 电子与信息学报, 2008, 30(11): 2674-2677.
QI Zisen, GUO Ying, WANG Buhong. Performance analysis of MUSIC for conformal array[J]. Journal of Electronics & Information Technology, 2008, 30(11): 2674-2677. (in Chinese)
[6] 齐子森, 郭 英, 姬伟峰, 等. 锥面共形阵列天线盲极化DOA估计算法[J]. 电子学报, 2009, 37(9): 1919-1925.
QI Zisen, GUO Ying, JI Weifeng, et al. Blind DOA estimation algorithm for conical conformal array antenna with respect to polarization diversity[J]. Acta Electronica Sinica, 2009, 37(9): 1919-1925. (in Chinese)
[7] QI Zisen, GUO Ying, WANG Buhong. DOA estimation algorithm for conical conformal array antenna[C]//IET 2009 international conference on RADAR. Guilin, China. 2009: 1-4.
[8] WORMS J G. Spatial superresolution with conformal array antennas[C]//Proc. 2000 IEEE Radar Conf. Alexandria, VA, 2000: 723-728.
[9] HWANG S, SARKAR T K. Direction of Arrival (DOA) estimation using a transformation matrix through singular value decomposition[C]//Proceedings of IEEE/ACES International Conference on Wireless Communications and Applied Computational Electromagnetic, 2005: 353-356.
[10] KIM K, SARKAR T K. DOA estimation utilizing directive elements on a conformal surface[C]// Proceedings of IEEE 2003 radar conference, 2003: 91-96.
[11] WORMS J G, Superresolution with conformal broadband antenna arrays[C]//Proc. 2002 IEEE Radar Conf. Long Beach, CA, 2002: 425-431.
[12] DO-HONG T, FISCH W, RUSSER P. Direction finding using spectral estimation with arbitrary antenna arrays[C]//Proceedings of IEEE MTT-S International Microwave symposium Digest, 2001: 1387-1390.
[13] 杨 鹏, 杨 峰, 聂在平, 等. MUSIC算法在柱面共形天线阵中的应用研究[J]. 电波科学学报, 2008, 23(2): 288-291.
YANG Peng, YANG Feng, NIE Zaiping, et al. DOA estimation of cylindrical conformal array by MUSIC algorithm[J]. Chinese Journal of Radio Science, 2008, 23(2): 288-291. (in Chinese)
[14] SCHMIDT R O. Multiple emitter location and signal parameter estimations[J]. IEEE Trans. Antennas and Propagation, 1986, 34(3): 276-280
[15] ROY R, KAILATH T. ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise[J]. IEEE Trans. on ASSP, 1986, 34(10): 1340-1342.
[16] 王布宏, 王永良, 陈 辉. 方位依赖阵元幅相误差校正的辅助阵元法[J]. 中国科学E 辑, 2004, 34(8): 906-918.
WANG Buhong, WANG Yongliang, CHEN Hui. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J]. Science in China, 2004, 34(8): 906-918. (in Chinese)
[17] PESAVENTO M, GERSHMAN A. Direction finding in partly calibrated sensor array composed of multiple subarrays[J]. IEEE Trans. on SP, 2002, 50(9): 2103-2115.
[18] 殷勤业, 邹理和, NEWCOMB R W. 一种高分辨率二维信号参量估计方法——波达方向矩阵法[J]. 通信学报, 1991, 12(4): 1-7.
YIN Qinye, ZHOU Lihe, NEWCOMB R W. A high resolution approach to 2-D signal parameter estimation-DOA matrix method[J]. Journal of China Institute of Communications, 1991, 12(4): 1-7. (in Chinese)
[19] SHAN T J, WAX M, KAILATH T. On spatial smoothing for estimation of coherent signals[J]. IEEE Trans. on ASSP, 1985, 33(4): 806-811.
[20] SHAN T J, WAX M, KAILATH T. Adaptive beamforming for coherent signals and interference[J]. IEEE Trans. on ASSP, 1985, 33(3): 527-536.
