立方氮化硼的电子结构与热力学性质研究

张淑华

（宜宾学院实验与教学资源管理中心，四川宜宾 644007）

立方氮化硼（c-BN）晶体是一种人工合成的超硬材料，在自然界没有天然的存在形式，它的莫氏硬度仅次于金刚石，而它比金刚石热稳定性好，化学惰性大，因而广泛应用于高温研磨、切削等场合［1］。另外，作为Ⅲ-Ⅴ族典型的化合物，立方碳化硼是性质优异的宽间接带隙半导体，广泛使用于电子、发光、薄膜等领域。由于立方氮化硼具有一些优异的物理、化学性质，许多学者对它进行了广泛的研究［2-9］，取得了一系列很有价值的结论。通过查阅资料文献，发现对立方氮化硼晶体材料的弹性与热力学性质的研究很少报道，现采用平面波赝势能方法，运用密度泛函理论对立方氮化硼晶体材料的弹性与热力学性质进行计算，为进一步研究与设计氮化硼晶体材料提供重要参考。

1 计算方法

计算是基于密度泛函理论的第一性原理方法，运用美国Accelrys公司的Materials Studio 4.0软件中的CASTEP软件包进行计算，它是基于密度泛函的从头算量子力学程序。利用总能量的平面波赝势方法，把离子势用赝势代替，电子波函数用平面波基组展开，电子与电子之间的相互作用的交换和相关势由广义梯度近似进行校正。在模型的结构优化中，采用BFGS算法，布里渊区积分采用Monkhorst-Pack的8×8×8进行分格，迭代过程中的收敛精度为5.0×10－6eV/atom，最大力收敛精度为0.01 eV/nm，最大应力收敛精度为0.02 GPa，最大位移收敛精度为5.0×10－5nm。电子的交换相互关联函数是 GGA-PBE，电子与离子间的相互作用则采用超软赝势（ultrsoft），平面波截断能量Ecut=280 eV，能量计算都在倒易空间中进行。

立方氮化硼晶体的空间群为F4－3 m，国际序号为216，晶胞中原子坐标为:B（0，0，0），N（0.250，0.250，0.250），结构如图1 所示，计算在一个原胞内进行。

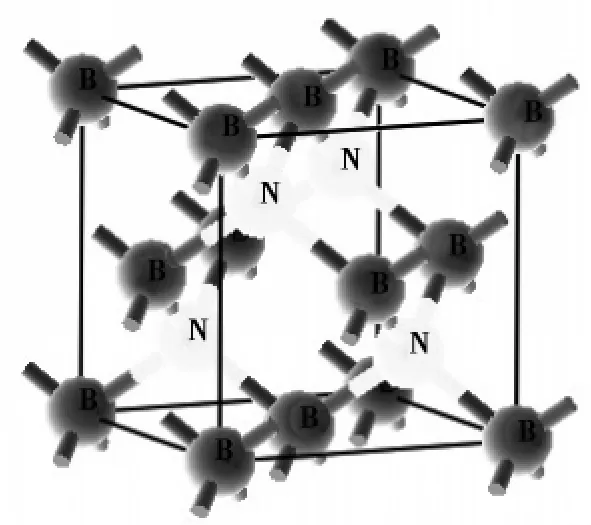
图1 立方氮化硼的晶体结构

经过几何优化，得到立方氮化硼晶体的晶格参数为0.359 3 nm，仅比实验值0.361 5小0.6%，电子结构与弹性常数的计算是基于这个优化结构，结果是可信的。

2 结果与讨论

2.1 电子结构

晶体的电子结构一般包括能带结构、态密度。在结构优化的基础上，利用GGA近似处理交换关联泛函，超软赝势处理离子实与价电子之间的相互作用，平面波基组描述体系电子的波函数，通过计算得到了立方氮化硼沿布里渊区高对称点方向的能带结构，形成3个带。价带的顶点在G点，导带的低点在X点，属于间接带隙，带隙宽度为4.654 eV，说明立方氮化硼为宽带隙半导体。具体结构如图2所示。

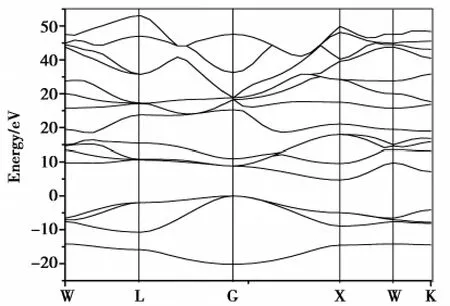
图2 立方氮化硼晶体的能带结构

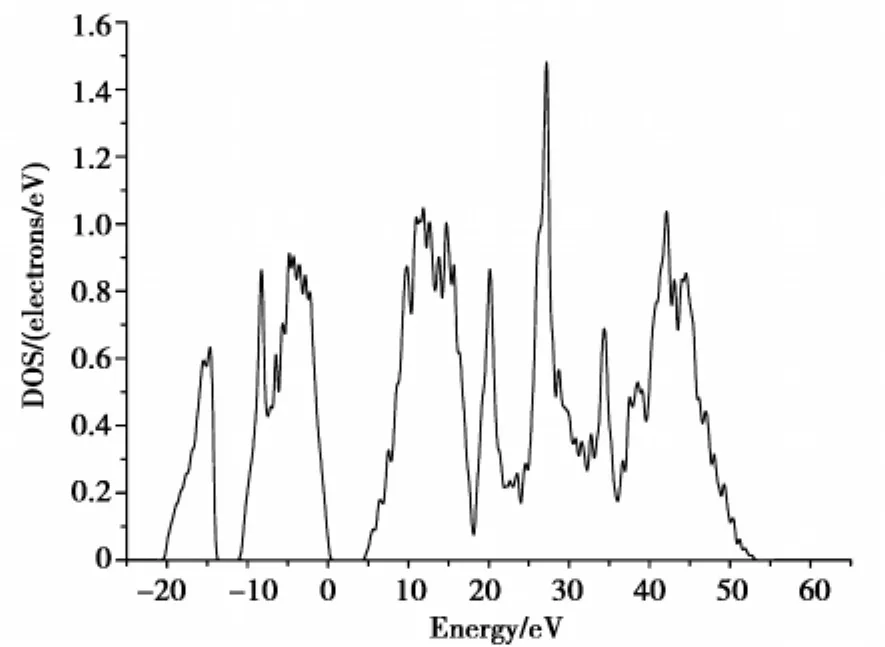
图3 立方氮化硼晶体的总态密度

立方氮化硼的总态密度图有3个连续区，对应于能带图中的3个带宽，如图3所示。导带跨度较大，能量从4.654 eV到53.064 8 eV之间，主要是鹏原子的2s2p1与氮原子的2s2p3轨道通过杂化所贡献。B－N键很强，所以化学惰性大，热稳定性好。

2.2 弹性

弹性在材料科学、化学、物理学及地球物理学等领域都是一个比较重要的研究对象。弹性性质影响晶体的许多其它固态性质，如状态方程、比热容、德拜温度、熔点等都与弹性相关。由弹性常数，可以获得晶体各向异性特点及晶体结构的稳定性等方面的重要信息。

立方氮化硼晶体的弹性张量Cij只有3个独立分量C11、C12及C44，通过几何优化之后计算出它在零温零压下的体弹模量及弹性常数如表1所示。

表1 零温零压下的体弹模量和弹性常数

2.3 德拜温度

由弹性常量可以通过式（1）－（7）求出德拜温度。

先由弹性常量通过Voigt-Reuss-Hill近似得到体弹模量和剪切模量。根据Voigt近似，剪切模量GV跟晶体的弹性常量Cij的有如下的关系:

根据Reuss近似，剪切模量GR跟晶体的弹性常量Cij的有如下的关系:

Hill从理论证明，多晶体模量刚好是Voigt和Reuss给出的算术平均值，即:

对于立方晶体，当p=0 GPa时，体弹模量B与弹性常量的关系为:

然后由剪切模量与体弹模量求出压缩纵波速和横波速分别为:

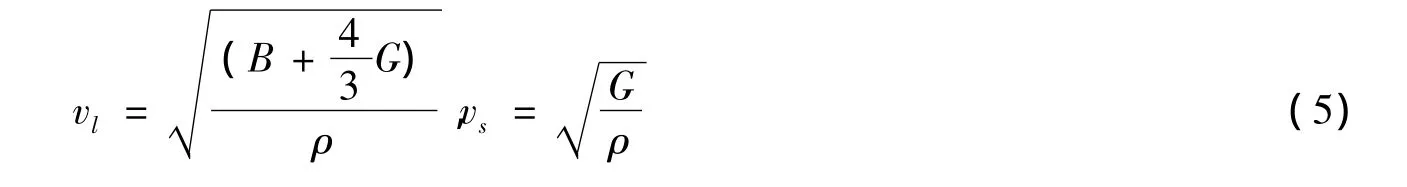
可得到平均声速:

最后由平均声速及德拜近似可求得德拜温度:

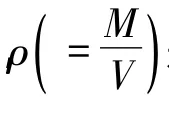
在零温零压下，通过以上式子的计算，最后得到立方氮化硼的德拜温度为θD=1 924.8 K，与他人计算结果1 900 K比较接近，红外线测得结果为1 700 K［11］，德拜温度直接反应晶体的热力学性质。

2.4 比热容

根据德拜模型近似，由德拜温度可以直接求出晶体的摩尔晶格内能:

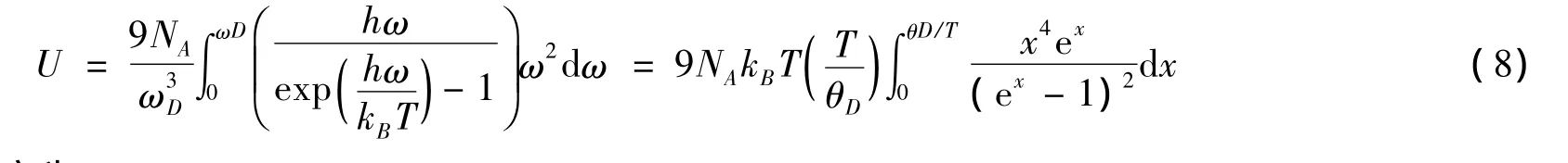
晶体的摩尔热容为:

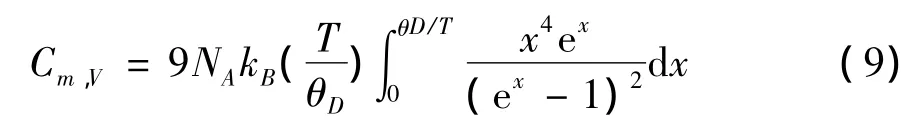
把计算得到的德拜温度代入式（9），通过数值计算可得热容随温度变化的具体图像（图4）。

从图4可以看出，当温度高于德拜温度时，热容随温度的变化非常小，逐渐接近25 J/mol·K（=3NAkB），当温度远高于德拜温度时，热容就为常数值25 J/mol·K，与杜隆－珀蒂定律一致;在温度远低于德拜温度1 924.8 K时，与德拜三次方定律很相符，说明我们从晶体的晶格常数出发求德拜温度是可靠的。

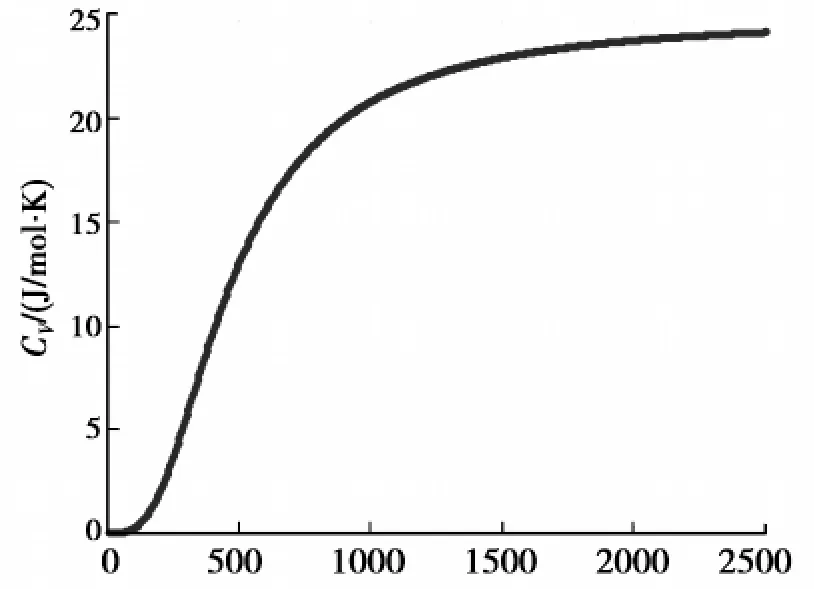
图4 立方氮化硼晶体的定容热容随温度的关系

3 结束语

采用第一性原理超软赝势平面波的方法，对立方氮化硼晶体结构进行了几何优化，得到晶格参数为0.359 3 nm;在优化结构的基础上计算得到带隙为4.654 eV，属于间接宽带隙半导体;零温零压下的弹性常数为C11=804.6 GPa、C12=161.2 GPa、C44=463.9 GPa及弹性模量B0=375.7 GPa;根据德拜模型近似，由弹性常量计算了德拜温度为1 924.8K，并进一步得到摩尔定容热容随温度的变化关系。为进一步研究立方氮化硼晶体材料的性质及材料设计提供了重要的参考。

［1］张铁臣，邹广田.立方氮化硼［M］.长春:吉林大学出版社，1993

［2］PASCALLON J，STAMBOULI V，ILIAS S，et al.Microstructure of c-BN Thin Films Deposited on Diamond Films［J］.Diamond and Related Materials，1999（8）:325-330

［3］ZHANG W J，BELLO I，LIFSHITZ Y，et al.Thick and Adherent Cubic Boron Nitride Films Grown on Diamond Interlayers by Fluorine-assisted Chemical Vapor Deposition［J］.Applied Physics Letters，2004，85（8）:1344-1346

［4］HUANG P C，YANG T S，CHU S S，et al.Structural Evolution of Boron Nitride Films Grown on Diamond Buffer-layers［J］.Thin Solid Films，2006（515）:973-978

［5］张铁臣，王明光，郭伟力，等.片状立方氮化硼合成及其导电特性研究［J］.高压物理学报，1998，12（3）:168-173

［6］杨杭生，聂安明，张健英.立方氮化硼薄膜的最新研究进展［J］.物理学报，2009，58（2）:1364-1370

［7］窦庆萍，马海涛.立方氮化硼晶体的电学性质与电流控制微分负阻［J］.中国科学E辑:技术科学，2008，38（11）:1952-1957

［8］何开华，郑广，吕涛，等.高压对氮化硼纳米管的几何结构、电子结构和光学性质的影响［J］.物理学报，2006，55（6）:2908-2913

［9］王光祖，李刚，张相法.立方氮化硼的合成与应用［M］.郑州:河南科学技术出版社，1995

［10］谢远亮，吴颖，罗宏超，等.用DFT计算立方氮化硼的状态方程及体积模量［J］.沈阳航空工业学院学报，2006，23（2）:80-82

［11］王光祖.立方氮化硼特性综述［J］.超硬材料工程，2005，17（5）:41-45