An Extending Method Based on the Masking Signal

LI Cui-wei，ZHAO Lin

（1.Academic Periodical Office，Chongqing Technology and Business University，Chongqing 400067 China;2.Testing Center of Mechanical Department，Chongqing University ，Chongqing 400044，China）

Hilbert-Huang Transform（HHT）is a new signal transform which is on the basis of instantaneous frequency defined by Hilbert Transform.This method has quite good characters to analyze non-stationary signal and non-linear signal.Successful applications of this method have varied from rainfall analysis to fault diagnosis of roller bearings［1］.

Despite the success of this analysis tool，there are several issues that require further attention for effective application of EMD.One of these issues is the end effect in EMD.The estimation of upper and lower envelopes as interpolated curves between extrema using cubic splines is a basic operation in EMD.In fact，it is not certain that the data of end is the local maxima or minima.The end data are not supported by whole signal，so the trend of end extreme points is uncertain.Treating the data of end as extreme points when interpolating by a cubic spline，the ends of time series will oscillate wildly.The end infection will propagate inwards and corrupt the subsequent lower frequency IMFs.At the beginning，the deviation brought by envelopes distortion only influences the both end，but with the processing of decomposition，it“contaminates”the whole signal series，the result of the sifting process is serious distortion.This is end effect of EMD.Furthermore，there is end effect in both end of signal，when Hilbert transformation is carried on.

In this paper，an improved end effect restraint technique based on the masking signal is proposed.The present method turned out to work effectively and it is heavily recommended for future EMD applications.The signal simulate test and engineering signal analysis prove that this improved method to deal with the end effects is effective.Furthermore，the improved EMD is applied to the fault diagnosis of gearbox.

1 The masking signal

The masking signal can solve the mode confusion of EMD，it can be described as:For a signalx（t），constructing a masking signals（t）［2］，and delimit:

Then taking for EMD separately tox+（t）andx－（t），obtaining the IMFh+（t）andh－（t），and delimitingh（t）as the IMF ofx（t）.

According to the energy mean method of IMF，the masking signal can be obtained.Detailed method:For a IMF obtained by normal EMDh1（t），and leth1（t）as:represents the average instantaneous frequency of IMF1，and it is lower than the highest frequency and higher than the lowest frequency.Choosing a masking signal of the form

The choice ofa0can affect the performance of the algorithm.Generally，the optimal choice ofa0depends on the frequencies and amplitudes of the components，but the factor of 1.6 above the average amplitude of the components is a decent rule of thumb.

The first method for dealing with the spline end conditions proposed by Huang is to pad the beginning and the end of the time series with additional“characteristic”or“typical”waves which reflect the characteristics frequency and amplitude of the signal.Huang et al.based their additional waves on the two closest maxima and minima［3］.The masking signal represents the average instantaneous frequency and the amplitudes information of IMF，it is based on the characteristics of the original signal，so we pad the beginning and the end of the time series with the masking signal.It is seen that the masking signal is sine signal，we can treat it as“typical”wave.According to the method Huang proposed，we extend two“typical”waves in both end of the original signal，which is based on the making signal.

To do the extending，we must make sure where the beginning of the“typical”waves of the masking signal is，making the extreme points of the endpoints as the judging benchmarks.The procedure is shown below:

1）Find the first and the last data of the time seriesx1andxk，the first and the last maximumu1andum，the first and the last minimumd1anddn（K，M，Nis respectively the number of the original data，the maximum data and the minimum data）.

2）Ifx1＞u1orx1＜d1，letx1be the maximum or minimum;Ifxk＞umorxk＜dn，letxkbe the maximum or minimum.

3）Then pad the beginning and the end of the time series with the masking signal waves from the maximum or minimum of wave.

4）Ifd1＜x1＜u1or dn＜xk＜um，comparex1（xk）closer tou1（um）ord1（dn）.

5）Then according to the method of waveform matching［4］，extracting the data betweenx1（xk）and the closest extremum to match withs（t）and obtaining the location of the extending wave.Let a0be the 1.6 above the average amplitude of the component.

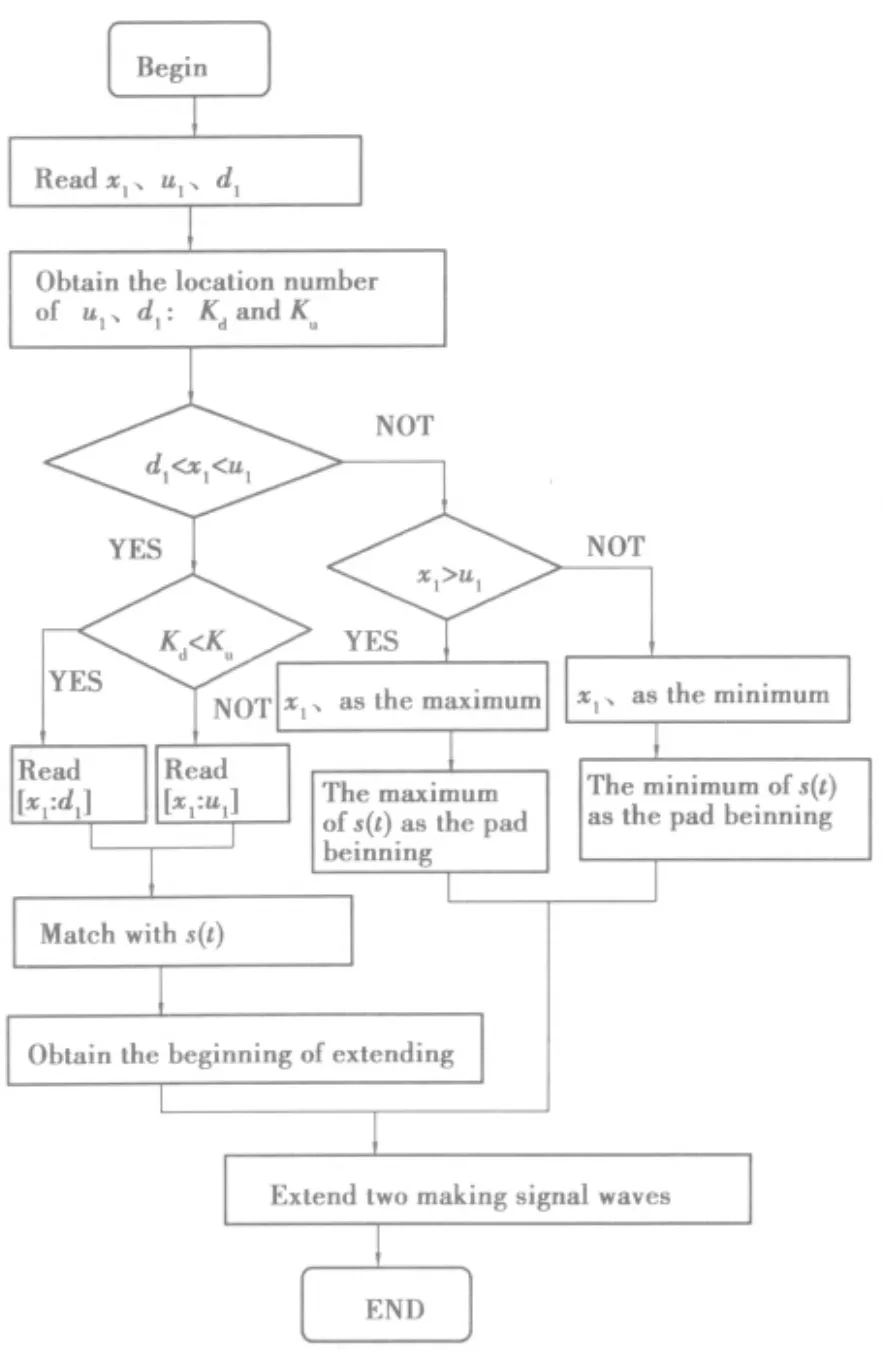
Fig1 flow diagram

The matching works is shown below:For two signals1（t）ands2（t），they have the same number of data.The similarity of waveforms can reflect their matching degree directly.LetP1（x0，y1）andP2（x0，y2）be two points ofs1（t）ands2（t）.Translatings1（t），and makingP1andP2coincidence，we can get a news'1（t）.This process is a process of align two waveforms along the reference point（Figure 2）.The matching degrees can be calculated by the following formula（7）;

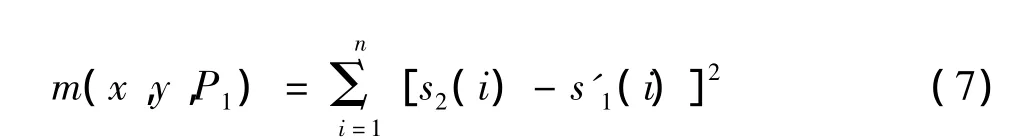
nis the sequence length.

Then，we extend the endpoint according to the waveforms that match for the highest.Because the original signal sequence is not long，and the length of the waveform ofs（t）is determined，the matching process is not complicated.

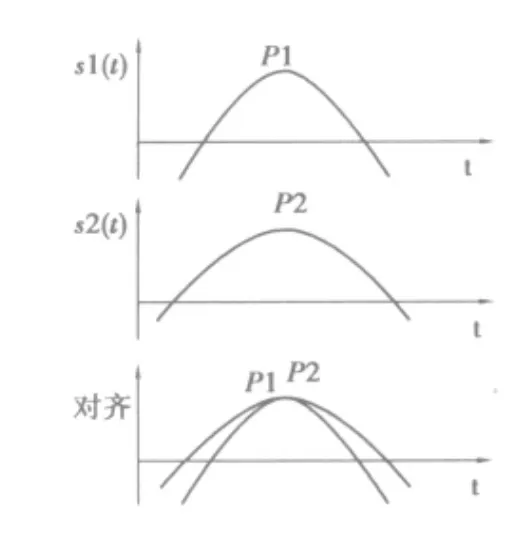
Fig 2 the calculation of matching degrees

2 Application

After EMD，we can obtain a series of IMFs of any signals，the given signalx（t）can be reconstructed by:

whereci（t）is the IMF component，andr（t）is the residue，nis the number of IMF.

In essence，EMD is an adaptive filtering process.For each IMF component，c1（t），…，cn（t）reflect the frequency bands from high to low，it can be regarded as a signalx（t）with bandwidth［0，fc］.Going through an ideal band-pass filter:

The result of the signal meets the requirements of IMF.Thereby，the first IMFc1（t）is obtained.Then in the bandwidth ［0，fc］，the second IMFc2（t）is obtained.Repeating the procedure，we can obtainc1（t），…，cn（t）and the residuer（t）.Let:

whereX（f）=FT{x（t）}（FT means to do Fourier transform），Hk（f）means the Kst filter.so，the Kst IMFck（t）=IFT{Ck（f）}，IFT means to do Inverse Fourier transform.For any two intrinsic mode function componentscj（t）andck（t），available by the Parseval theorem:

All these can prove that any two intrinsic mode function componentscj（t）andck（t）are orthogonal between each other.Its transformation does not affect the function expressed by itself.

That is why we can deal with end effect to every IMF component of the original signal separately.After extending both edge of IMF1，the additional extremum can be obtained.With cubic spline interpolation，we calculate the upper and lower envelopes，and get the mean.Fig 3 shows the envelopes we got after extending the endpoint.It is clear that the endpoint of envelope and signal at the two ends are no longer overlap.Repeating the procedure to deal with the follow-up IMF components，and the result of EMD is shown in Fig4.The results are basically no distortion.

Because the mask signal itself can reflect the certain frequency and amplitude characteristics of the IMF，for each IMF after extending endpoint，the signal is closer to the original signal.Correction of the upper and lower envelopes can improve the accuracy of the EMD.For Hilbert Transform，because the distortion of instantaneous energy spectrum of signal focuses on the two ends，we pad the endpoints，and then truncate the extending data after transforming to suppress the end effect.Its theoretical evidence is the Hilbert transform which can be regarded as original data to do 90 °phase-shift.Therefore，any corresponding section of data is the dual signal［5］.

3 Conclusion

The newly developed end effect restraint technique based on the masking signal has been presented in this paper to improve the EMD method and Hilbert transform.Because the masking signal reflects the certain frequency and amplitude characteristics of the IMF，the extending signal is similar to the original signal.Result of simulation and experiment shows that end effect can be effectively restrained.

Reference:

［1］NORDEN E H，ZHENG S，STEVEN R L ，et al.The empirical mode decomposition and the Hilbert spectrum for non－linear and non－stationary time series analysis［J］.Proceedings of the Royal Research，2004（26）:1-12

［2］程军圣，于德介，杨宇.基于支持矢量回归机的Hilbert—Huang变换端点效应问题的处理方法［J］.机械工程学报（Chinese J Mechanical Eng.），2006，42（4）:23—31

［3］ DEERING R，KAISER J .The use of a masking signal to improve empirical mode decomposition.ICASSP［A］.IEEE International Conference on Acoustics，Speech and Signal Processing – Proceedings［C］.2005.（4）:485-488

［4］任达千，吴昭同，严拱标.EMD端点效应的评价指标及抑制端点效应的窗函数法［J］.制造业自动化，2007（1）:21－24

［5］邵晨曦，王剑，范金锋，等.一种自适应的的EMD端点延拓方法［J］.电子学报，2007（10）:1944－1948