关于两个有穷级整函数的唯一性

夏生虎

（重庆大学 数理学院，重庆 400044）

设f表示一个开平面上的非常数整函数，采用亚纯函数NevanLinna理论的标准记号，特别地，用

S（r，f）表示任意满足S（r，f）=O{T（r，f）（r→∞ ，rE）}的量，其中E是一个有穷线性测度集.

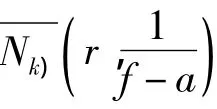
对有穷级整函数，仪洪勋证明了:

林伟川，吕巍然证明了:

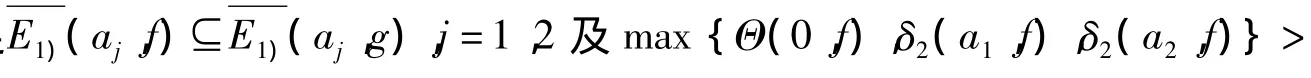
1 主要结果

在改进上述定理的情况下，得到下列结果:

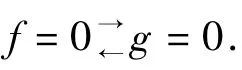
2 引理

引理1 设f（z）与g（z）为开平面上非常数亚纯函数，其级分别为λ（f）与λ（g），如果λ（f）＜λ（g），则λ（fg）=λ（g），λ（f+g）=λ（g）.

引理2［3］设h（z）为非常数整函数，f（z）=eh（z），且f（z）的级为 λ，下级为 μ.

i）若h（z）为P次多项式，则λ=μ=P;ii）若h（z）为超越整函数，则λ=μ=∞.

引理3 设f（z）与g（z）为开平面上的非常数亚纯函数，其级分别为 λ（f）与 λ（g），则 λ（fg）≤max{λ（f），λ（g）}，λ（f+g）≤max{λ（f），λ（g）}.

证明 由NevanLinna第二基本定理得:

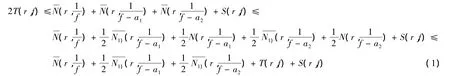
结合引理的条件，由式（1）得:

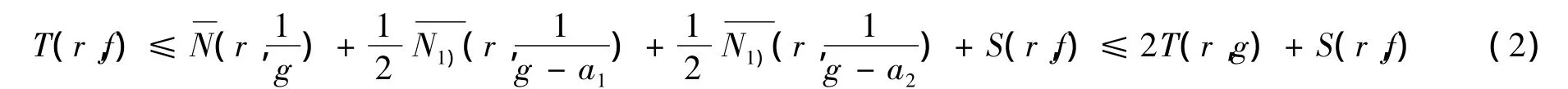
由于g（z）的级λ（g）为有穷非整数，故由式（2）可推得:

下面分两种情况讨论.

①若f（z）≡g（z），则λ（f）=λ（g），引理成立.

②若f（z）不恒等于g（z），设:

由f=0→←g=0得F（z）=eh（z），其中h（z）为整函数，利用引理2，即得λ（eh）为整数，同时由式（4）及引理（3）可得:

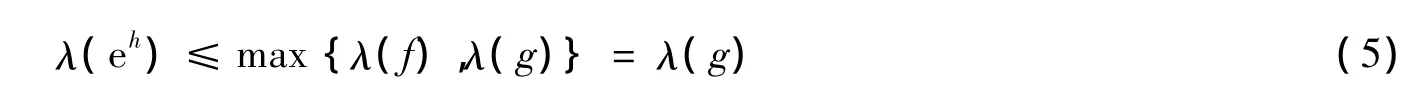
由于λ（g）为有穷非整数，所以λ（eh）＜λ（g）由引理（1）得:

3 定理的证明

定理5的证明 假设f（z）不恒等于g（z），根据定理条件及引理4与式（4）（6）可得:

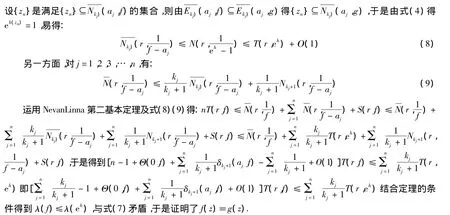
定理6的证明 由定理1的证明得:

［1］仪洪勋，杨重骏.亚纯函数唯一性理论［M］.北京:科学出版社，1995

［2］林伟川，吕巍然.有穷级整函数的唯一性［J］.福建师范大学学报，2001（2）:6-9

［3］HAYMAN W.Meromorphic Functions［M］.Oxford，1964