水下航行器动力装置振动频率自动识别方法

孙 涛, 高爱军, 王 袆



水下航行器动力装置振动频率自动识别方法

孙 涛, 高爱军, 王 袆

(中国船舶重工集团公司第705研究所, 陕西 西安, 710075)

为满足水下航行器动力装置振动试验研究对频谱分析的及时性要求, 本文以分析对象振动信号的频谱特征和离散傅里叶变换的数学原理为基础, 将频谱细化算法和峰值搜寻算法有机结合, 构造了一种振动频率自动识别准确率高的自动频谱分析方法, 并设计编制了模块化架构的程序。该方法利用频谱细化算法准确计算动力装置周期性激励源的测试频率, 利用峰值搜寻算法有效提取振动信号优势成分, 以筛分出的峰值频率和周期性激励理论频率的一致性程度来确定振源, 通过仿真信号和工程实际振动信号进行应用分析。分析表明, 该方法可明显提高试验数据的分析效率和准确性。

水下航行器; 动力装置; 振动频谱; 自动识别; 模块化

0 引言

在几乎所有的机械工程部门, 如机床、飞机、舰船、汽轮机、压缩机等机械装备中, 信号处理一直是振动控制、故障诊断、模态分析的基础, 而运用广泛且卓有成效的信号处理方法则是在数学理论和快速算法上已取得重大突破的频谱分析方法。目前, 频谱分析已成为各类商用振动分析软件必不可少的功能。虽然商用振动分析软件提供的频谱分析功能具有计算精度高、计算速度快、操作界面友好等优点, 但是它们只能对输入信号进行傅里叶变换生成频谱, 而判定谱峰频率对应何种振动原因还需依赖人工进行, 这种分析方式越来越不能满足振动激励源查找、振动控制效果评判、振动传递路径识别、复杂机械故障诊断等对海量振动数据分析处理的及时性要求, 如何快速准确地识别谱峰频率的成因已成为深入应用频谱分析方法迫切需要解决的难题。

近些年来, 为了保障流程工业中重大关键设备(如汽轮机、压缩机等)的安全高效运行, 各种专用智能故障诊断系统陆续被研制出来并投入使用, 极大地推动了振动频谱自动识别技术的研究。阮跃论述了建立汽轮发电机组振动频谱自动识别的原则及典型故障振动频谱特征可信度的计算方法[1]。卢学军等根据汽轮发电机组的典型振动故障频率征兆表, 提出了基于振动频谱自动识别的综合自动诊断方法[2]。近年来兴起的小波变换能同时提供振动信号的时域和频域的局部化信息, 为机械故障诊断提供了一种强有力的分析手段。王平等将小波包分析引入滚动轴承振动频谱的自动识别, 提出了基于小波包分析和包络检测的滚动轴承故障特征信息的自动提取方法[3-4]。这些振动频谱自动识别方法主要适用于汽轮机、滚动轴承等振动故障频率分布有规律可寻的通用机械设备或机械部件的智能故障诊断, 对于典型振动频率征兆表尚未建立或很难建立的机械设备的振源查找、振动特性分析等则不太适用。

某水下航行器动力装置(简称动力装置)为外燃机, 结构复杂, 零部件众多, 其振动频谱常包含多种振动源频率, 各振动源特征频率的倍频及伴有的边频带导致频谱图中线谱很复杂。为满足研究其振动特性和查找振源对海量振动试验数据分析处理的及时性需求, 本文提出基于离散傅里叶变换(discrete fourier transform, DFT)的振动频率自动识别方法, 利用Matlab语言开发了通用的自动识别程序, 大大提高了试验数据分析效率, 可有效缩短试验周期, 具有重要的工程价值。

1 通用振动分析软件的频域分析流程

工程上所测得的信号多为时域信号, 为了通过所测得的时域信号了解观测对象的动态行为, 往往还需要从频域描述一个随机信号的特征, 以便获得频域信息, 这种把时域信号变换至频域加以分析的方法称为频谱分析。频谱分析的目的是把复杂的时间历程波形, 经过傅里叶变换分解成若干单一的谐波分量, 并研究各谐波分量的幅值和相位信息, 从而获得信号的能量沿频带的分布情况[5]。随着大规模集成电路的迅速发展, 尤其是在1965年, Cooly-Tukey发明了一种快速傅里叶变换算法(fast fourier fransform, FFT), 把傅里叶变换的时间减少了几个数量级, 极大地推动了频谱分析技术的工程应用, 目前频谱分析已成为通用振动分析软件必不可少的功能。

通用振动分析软件的频谱分析流程: 首先, 从记录有测试数据的数据库中选择待分析的信号; 其次, 利用软件提供的频谱分析功能对输入信号进行傅里叶变换生成频谱; 最后, 人工判定谱峰频率和振源的对应关系。这种分析方式效率非常低, 无法满足试验研究对数据分析处理的及时性要求, 如何快速准确地识别出谱峰频率和振源的对应关系已成为迫切需要解决的问题。

2 振动频率自动识别方法原理及技术实现

动力装置振动信号的频谱特点具有一般性, 其特点主要包括: 1) 包含与各组部件工作相关的多种振动频率; 2) 各种振动源特征频率往往出现高阶倍频成分。为了满足动力装置振动试验对数据分析处理的及时性要求, 本文将动力装置振动信号的频谱特点和DFT的特点相结合, 构造出一种振动频率自动识别方法。

2.1 振动频率自动识别方法原理

大量的动力装置振动频谱分析表明, 频谱中主要的离散谱分量对应动力装置的典型周期性激励源的特征频率(发动机轴频、辅机轴频、辅机压力脉动频率等)。在动力装置转速已知条件下, 这些周期性激励源的特征频率可通过理论计算得到。

通过计算机对振动信号进行频谱分析, 本质上是进行DFT, 即将个时间域的采样序列和个频率域采样序列联系起来, DFT的公式如下[6]

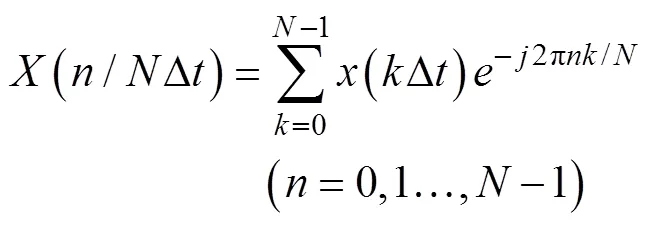
2.2 振动频率自动识别方法的程序实现

振动频率自动识别方法的程序采用模块化设计, 模块划分如1所示, 各模块功能定义: 1)输入模块: 读入振动测量数据; 2)FFT计算模块: 完成时域到频域的变换; 3)筛分模块: 从幅值序列中筛分出满足条件的幅值样本; 4)振源定位模块: 根据筛分出的频率和动力装置典型周期性激励源频率的匹配程度确定振源; 5)输出模块: 按要求格式输出分析结果。

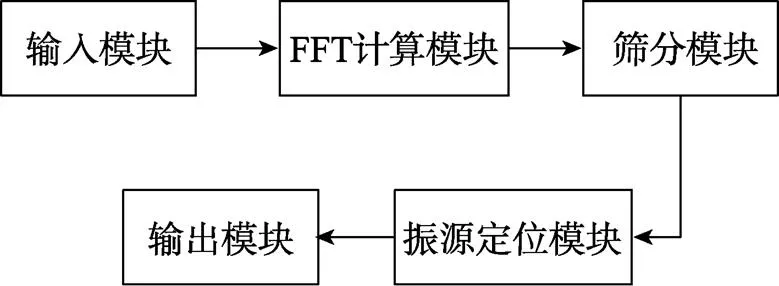
图1 程序模块

在上述5个模块中, 筛分模块和振源定位模块是核心模块。筛分模块利用经验模态分解(empirical mode decomposition, EMD)[7]确定局部极值点的方法从幅值序列中确定出极大值序列, 从而有效筛分出满足条件的幅值样本。

该动力装置为外燃机, 其传动方式决定了典型激励源频率均和发动机主轴的轴频有关, 根据筛分频率和典型激励源频率来识别振源时, 首先, 需要确定高精度的发动机轴频, 本程序利用FFT- FT频率细化方法[8]计算发动机轴频, 为计算精度高的典型激励源倍频奠定了基础; 其次, 综合考虑由发动机轴频推导倍频时的频率误差累积和FFT的频率分辨率误差, 确定出计算频率和测量频率是否匹配的评判阈值, 通过比较每个筛分频率和典型激励源频率的前100阶倍频的频率差是否满足阈值要求, 初步识别出振源。进而利用信号的先验知识调整参与比较的典型激励源频率的种类, 并且结合筛分频率的频率间隔是否存在倍数关系等辅助信息以及人工经验给出最终的识别结果。

3 应用分析

3.1 仿真应用分析

为验证本方法对振动频率的自动识别效果, 此处任意构造一个由若干简谐信号叠加形成的周期信号为例来说明。考察式(2)所示的仿真信号

信号()中包含1(50 Hz)的1倍频和2倍频,2(100 Hz)的2倍频和3倍频,3(150 Hz)的1倍频和3倍频, 共6个频率成分, 其时域波形和幅值谱如图2所示。

图2 仿真信号的时域波形和幅值谱

Fig. 2 Time-domain waveform and amplitude spectrum of simulated signal

筛分条件设置为输出前6个最大值, 程序的输出结果如表1所示。可以看出, 自动识别程序不但准确找出了仿真信号中的6个频率成分, 而且自动判别出了每个频率成分对应的可能振动原因。将程序的输出结果和信号的先验知识相结合即可判断出每个频率成分对应的振动原因, 最终的分析结果见表2。

3.2 工程实例

动力装置能供系统的泵径向测点振动信号()的时域波形和幅值谱如图3所示, 可以看出, 谱峰主要分布在频段1和频段2。频段1中最高谱峰对应的幅值为0.009, 频段2中最高谱峰对应的幅值为0.005, 前者的幅值基本等于后者幅值的2倍, 为了筛分时不漏掉在各自频段占主要振动能量的频率成分, 分析时对这2个频段设置不同的筛分条件。频段一的筛分条件为该频段最大幅值的20%, 频段二筛分条件为该频段最大幅值的30%。将程序的输出结果和信号的先验知识相结合即可判断出从频段一中筛分出的频率成分除了该泵压力脉动频率的前3阶倍频成分, 其他都是发动机的轴频; 频段二中的离散谱峰全为该泵压力脉动频率的倍频, 范围为15~39阶。

表1 仿真信号频谱自动识别初步结果

表2 仿真信号频谱自动识别最终结果

图3 振动信号h(t)的时域波形和幅值谱

虽然该自动识别程序输出结果的最终确定仍需人工参与, 但由于程序自动从FFT计算结果所产生的成百上千的频率成分中筛分出符合条件的频率成分, 并在表格中自动填入相关信息, 完成振源定位的大部分分析工作, 所以大大降低了分析强度和时间。此外, 人工判定谱峰对应何种特征频率一般采用查表方式, 一旦看到和某振源频率相近便判定由该振源引起, 往往导致误判。因此, 自动识别程序列出频率成分对应的所有可能振动原因一定程度上会提高分析的准确性。

4 结束语

动力装置结构和工况复杂, 零部件众多, 建立能较好模拟其振动特性的数学模型相当困难, 振动试验仍然是目前研究动力装置振动特性的主要手段。频谱分析是振动数据处理长期有效的工具, 本文结合动力装置振动信号的频谱特点和DFT变换的特点, 构造出一种动力装置振动频率自动识别方法, 较好地解决了通用振动分析软件无法根据振动信号频谱特征自动确定激振原因的局限性, 大大提高了动力装置频谱分析的效率。本方法的原理具有一般性, 可用于设计各种机械设备的振动频率自动识别程序, 针对动力装置开发的程序在实际工作中已用于振源查找、故障诊断等, 取得了较好的效果。

[1] 阮跃. 汽轮发电机组振动频谱的自动识别[J]. 电站系统工程, 2000, 16(1): 45-47. Ruan Yue.Auto-Recognition of Vibration Spectrum of Steam Turbine-Generator Units[J].Power System Engineering, 2000, 16(1): 45-47.

[2] 卢学军, 缪思恩, 顾晃. 汽轮发电机组振动故障的综合自动诊断方法研究[J]. 中国机械工程, 2002, 13(14): 1193- 1195. Lu Xue-jun, Liao Si-en, Gu Huang. Study on the Comp- rehensive Automatic Fault Diagnosis Method for Turbine Generator Sets[J]. China Mechanical Engineering, 2002, 13(14): 1193-1195.

[3] Mallet S G. A theory for Multi-resolution Signal Decomposition: the Wavelet Representation[J]. IEEE Transactions. on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.

[4] 王平, 廖明夫. 滚动轴承故障特征信息的自动提取方法研究[J]. 机械强度, 2003, 25(6): 604-609. Wang Ping, Liao Ming-fu. Auto-Extraction of Fault Features in Rolling Element Bearing Fault Diagnosis[J].Journal of Mechanical Strength, 2003, 25(6): 604-609.

[5] 谷立臣. 机械信号处理及应用[M]. 西安: 陕西科学技术出版社, 2000.

[6] 何正嘉, 訾艳阳, 张西宁. 现代信号处理技术及应用[M]. 西安: 西安交通大学出版社, 2006.

[7] Huang N E, Shen Z, Long S R. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[C]//proceedings: Math- ematical, Physical and Engineering Sciences of the Rouyal Society, 1998: 903-995.

[8] 刘进明, 应怀樵．FFT谱连续细化分析的富里叶变换法[J]．振动工程学报, 1995, 5(2): 162-166. Liu Jin-ming, Ying Huai-qiao. Zoom FFT Spectrum by Fou- rier Transform[J]. Journal of Vibration Engineering, 1995, 5 (2): 162-166．

An Automatic Recognition Method of Vibration Frequency for Underwater Vehicle Power System

SUN Tao, GAO Ai-jun, WANG Yi

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

To satisfy the timely demand of vibration spectrum analysis for underwater vehicle power system in vibration test, on the basis of the signal spectrum feature and discrete Fourier transform(DFT)principle, an automatic vibration fre- quency recognition method is presented via zoom-FFT(fast Fourier transform)combining with peak search algorithm, and the corresponding modularized program is coded. The method uses zoom-FFT to calculate the exact measuring frequency of the power system periodic motivation, and utilizes peak search algorithm to extract the dominant frequency component in order to confirm the vibration source with the consistent degree of two kinds of frequencies. The application of the present method to simulated signal and real signal shows the analysis efficiency and accuracy are improved markedly.

underwater vehicle; power system; vibration spectrum; automatic recognition; modularization

TB53

A

1673-1948(2011)02-0120-04

2010-03-10;

2010-04-14.

孙 涛(1977-), 男, 博士, 主要研究方向为机械信号处理、振动测量和控制、振动一致性评判与诊断.

(责任编辑: 陈 曦)