自航水雷落入预定障碍区域概率模型

冷相文, 赵晓哲, 张 旭, 朱红波



自航水雷落入预定障碍区域概率模型

冷相文1,2, 赵晓哲2, 张 旭2, 朱红波1,2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 海军大连舰艇学院 水武与防化系, 辽宁 大连, 116018)

基于自航水雷(SLMM)的使用特点, 提出了计算自航水雷落入预定障碍区域概率的2种方法——直接法和间接法, 并建立了相关理论模型, 通过仿真实例对这2种模型进行了计算和验证, 从方法体现的规律性、计算精度及适应性3个方面对仿真结果进行了分析, 相关结论可用于自航水雷雷位散布特性研究及水雷障碍结构优化。

自航水雷; 概率模型; 预定障碍区域; 仿真

0 引言

自航水雷是一种由平台发射后可依靠自身动力航行至预定水雷障碍区的水雷。与其他水雷相比, 它具有可对布雷平台不易或无法接近的敌港口和航道等水域实施布雷封锁的优势。但实际的布放过程中, 自航水雷需要航行相当长的距离。由于受水雷航行误差和布雷平台误差等因素的影响, 自航水雷达到的实际位置相对于预定位置的偏差具有较大的随机性, 这种随机性将直接关系到自航水雷能否落入预定障碍区域。因此, 自航水雷落入预定障碍区域的概率大小是其散布特性表现的一个主要方面。

本文根据自航水雷的散布特点, 建立了自航水雷落入预定障碍区域概率的“直接”与“间接”2种计算方法的相关模型。

1 “直接法”理论模型

所谓“直接法”是指在综合考虑自航水雷雷位散布误差的基础上, 确定其落入预定障碍区域的概率, 并根据不同障碍样式得到落入该障碍区域内的期望水雷数。

首先建立以水雷障碍正面宽度的中点作为坐标原点, 水雷障碍的正面方向为轴的平面坐标系, 水雷障碍区域的4个顶点为,,,其坐标如图1所示。

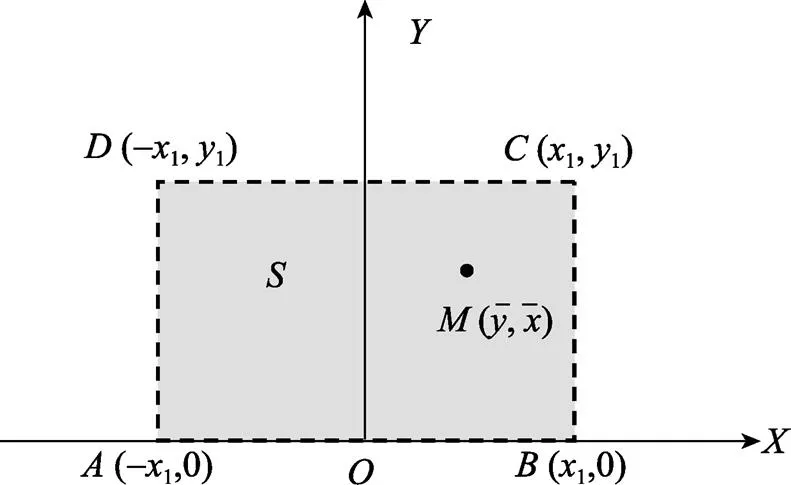
图1 预定水雷障碍区域坐标系

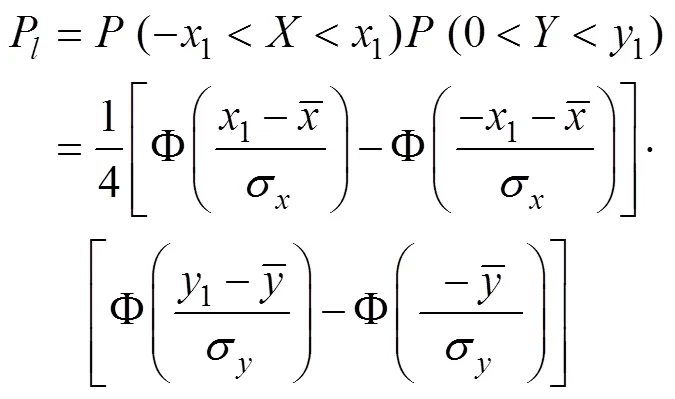
需要强调的是, 在布设单一雷群或雷线时, 各枚自航水雷期望雷位点是不相同的, 因此, 自航水雷落入该区域的概率也就不同, 从而影响其落入该区域的期望雷数。

1.1 布设单一雷群时落入障碍区域的概率模型

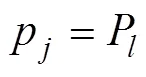
式中:p为第枚水雷落入预定障碍区内的概率, 由式(1)确定。

因此,枚自航水雷中至少1枚落入预定障碍区内的概率为

式中:为落入预定障碍区内的水雷个数,≤。

1.2 布设雷线时落入障碍区域的概率模型

在自航水雷布设雷线样式的水雷障碍时, 第枚自航水雷雷位点(X,Y) (=1, 2,…,)的期望位置可由下式确定

此种情况下, 第枚自航水雷落入预定障碍区内的概率P可以通过式(1)得出, 但由于各枚自航水雷的期望雷位点有所不同, 它们落入预定障碍区内的概率也不尽相同。如此,枚自航水雷中至少1枚落入预定障碍区内的概率为

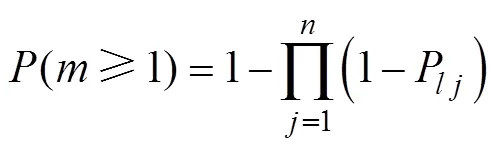
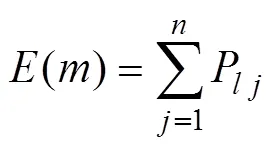
2 “间接法”理论模型

“间接法”的基本思想是以雷位次序坐标分布期望均值的点估计为基础, 近似计算自航水雷落入预定障碍区域概率的一种方法。

根据文献[4]可知(s)的均值为

式中

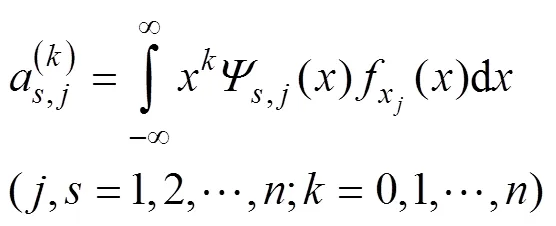
其中,F()为X的分布函数。

而[s]的分布密度函数为

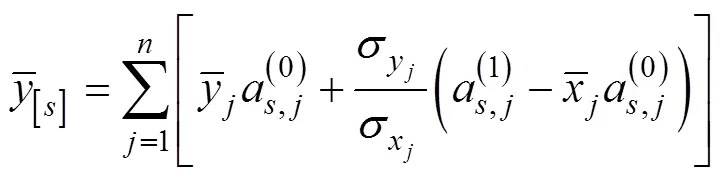
当雷位期望次序坐标满足下列条件

则认为该枚自航水雷落入预定障碍区域。因此, 自航水雷落入预定障碍区域的近似概率可表示为

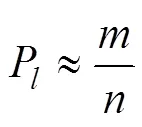
式中:为落入预定障碍区域内的水雷数(0≤≤)。

3 仿真

由于影响自航水雷雷位散布的因素很多, 因此, 采用蒙特卡洛方法建立仿真模型[5]。

根据文献[6]提供的方法, 首先产生相互独立的2D标准正态分布随机数(1,2)

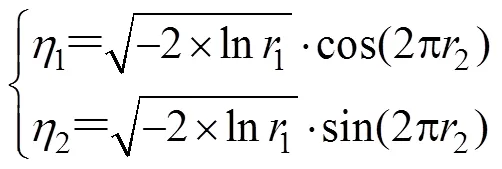
式中,1,2为2个(0, 1)均匀分布随机数。

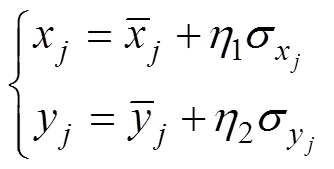
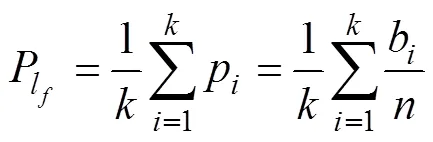
4 实例计算与结果分析

表1 水雷落入预定障碍区概率的理论值与仿真值

通过对表1中所示的不同情况下相应的理论值和仿真结果进行对比分析, 可以得出如下结论。

2) 从计算的精度讲, 在相同条件下, 采用“直接法”计算自航水雷落入预定障碍区域概率的理论值和仿真结果非常接近, 最大绝对差值不到0.01。据此说明“直接法”理论模型具有较高的精度。而采用“间接法”得到的相应概率与仿真值虽存在一定偏差, 但二者的绝对偏差不超过0.13, 究其原因是由于“间接法”是从统计意义上得到的自航水雷落入预定障碍区域概率的近似值, 并且此概率的近似值是由于落入预定障碍区的期望水雷数取整, 引起随着水雷数量的增加而出现了一些波动。

3) 从方法的适应性来说, 由于考虑到不同障碍样式下各枚水雷的散布情况, 因此采用“直接法”计算自航水雷落入预定障碍区域概率具有更为广泛的适应性, 而在某些特定的情况下, 如布雷决策者需对所布自航水雷进入预定障碍区的概率及水雷数量进行快速、概略估算时, 可考虑适时使用“间接法”。

4) 对于任意自航水雷雷位坐标(,)而言, 本文对其随机变量,不相互独立而存在。r取值的不同条件下, 自航水雷落入预定障碍区域的概率进行了计算和仿真,所得到的结果表明, 在其他条件相同的情况下, 水雷落入预定障碍区域的概率随r的变化不明显。

[1] ВМШ. Тактическое Руковотсво по Боевой Деятельн ости[M]. С-Петербург: ВМА, 1989.

[2] В.П.Кузин,В.И.Никольский.Военно-Морской Флот ССС Р[M]. Историческое Морское Общество, 1999.

[3] Ю.А.Коробов. Боевое Применение Минного И Про- тивоминно Оружия[M]. С-Петербург: ВМА, 1995.

[4] 张旭, 冷相文. 自航水雷雷位次序坐标散布特性[J], 火力指挥与控制, 2004, 29(4): 47-51. Zhang Xu, Leng Xiang-wen. The Distributed Characteristics of Ordering Coordinates of SLMM's Position[J]. Fire Co- ntrol & Command Control, 2004, 29(4): 47-51.

[5] 齐欢. 系统建模与仿真[M]. 北京: 清华大学出版社, 2004.

[6] 何江华, 郭果敢.计算机仿真与军事应用[M].北京: 国防工业出版社, 2004.

Two Probability Model of SLMM Hitting Predetermined Obstacle Zone

LENG Xiang-wen1, 2, ZHAO Xiao-zhe2, ZHANG Xu2, ZHU Hong-bo1, 2

(1. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China; 2. Department of Underwater Weaponry and Chemical Defense, Dalian Naval Academy, Dalian 116018, China)

Based on the operational specialty of submarine launched mobile mine(SLMM), two general models which describe the probability of SLMM hitting predetermined obstacle zone were established. Two examples were simulated to verify the models. The simulation results of both models concerning regularity, accuracy and adaptability were compared. The conclusions may be applied to the analysis of characteristics of SLMM position dispersion and the optimization of mine obstacle configuration.

submarine launched mobile mine (SLMM); probability model; predetermined obstacle zone; simulation

TJ6; E925.23

A

1673-1948(2011)01-0059-04

2009-11-19;

2010-03-26.

海军大连舰艇学院科研发展基金(2009032).

冷相文(1978-), 男, 博士, 讲师, 主要研究方向为武器总体设计理论与方法.

(责任编辑: 陈 曦)